第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「整流回路の原理(整流ダイオードとサイリスタ)」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「整流回路の原理(整流ダイオードとサイリスタ)」の過去問題も解説しています。
- 整流回路
- 単相半波整流回路
- 単相全波整流回路(単相ブリッジ整流回路)
- 三相半波整流回路(三相ブリッジ整流回路)
- 三相全波整流回路(三相ブリッジ整流回路)
- 交流電力調整装置
- 電験三種-機械の過去問解説:整流回路の原理
- 1999年(平成11年)問5
- 1999年(平成11年)問5 過去問解説
- 2003年(平成15年)問9
- 2003年(平成15年)問9 過去問解説
- 2004年(平成16年)問9
- 2004年(平成16年)問9 過去問解説
- 2005年(平成17年)問9
- 2005年(平成17年)問9 過去問解説
- 2006年(平成18年)問9
- 2006年(平成18年)問9 過去問解説
- 2007年(平成19年)問9
- 2007年(平成19年)問9 過去問解説
- 2007年(平成19年)問16
- 2007年(平成19年)問16 過去問解説
- 2010年(平成22年)問16
- 2010年(平成22年)問16 過去問解説
- 2011年(平成23年)問9
- 2011年(平成23年)問9 過去問解説
- 2011年(平成23年)問17
- 2011年(平成23年)問17 過去問解説
- 2012年(平成24年)問10
- 2012年(平成24年)問10 過去問解説
- 2013年(平成25年)問9
- 2013年(平成25年)問9 過去問解説
- 2014年(平成26年)問10
- 2014年(平成26年)問10 過去問解説
- 2016年(平成28年)問16
- 2016年(平成28年)問16 過去問解説
- 2017年(平成29年)問11
- 2017年(平成29年)問11 過去問解説
- 2017年(平成29年)問16
- 2017年(平成29年)問16 過去問解説
整流回路
交流を直流に変換することを整流といい、そのための回路を整流回路といいます。整流回路は、ダイオード、トランジスタ、サイリスタなどの半導体素子を用いて構成されており、整流回路は大きく分けると次の4つがあります。
- 単相半波整流回路・・・単相交流の(波形の) 半分を整流する回路
- 単相全波整流回路・・・単相交流の(波形の) 全てを整流する回路
- 三相半波整流回路・・・三相交流の(波形の) 半分を整流する回路
- 三相全波整流回路・・・三相交流の(波形の) 全てを整流する回路
単相半波整流回路
図2(a)は整流素子としてサイリスタを使用した単相半波整流回路で、図(b)は抵抗負荷の場合の電圧と電流の関係を示し、図(c)は誘導性負荷の場合の電圧と電流の波形です。
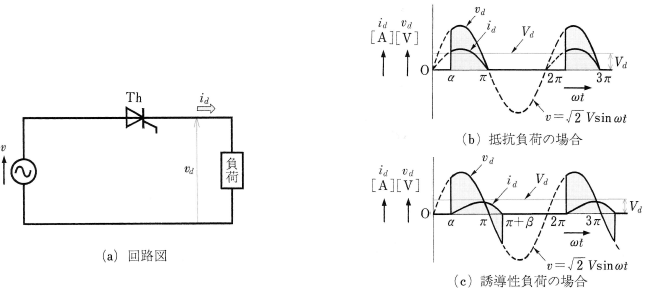
電源電圧 $v=\sqrt{2}Vsinωt$[V]の位相 $ωt$ が 0~$π$[rad]の間において、位相角 $α$[rad]のときサイリスタをターンオンさせると、電流 $I_d$[A]が流れます。$ωt$ が $π$~$2π$[rad]では、サイリスタには逆方向電圧が加わるので、ターンオフし、$I_d$ は 0 Aとなります。したがって、直流平均電圧 $V_d$[V]は次の式で表すことができます。
サイリスタを使った単相半波整流回路の直流平均電圧を求める式
$V_d≒0.45V\displaystyle\frac{1+cosα}{2}$
$V_d$[V]:直流平均電圧
$V$[V]:交流電圧の実効値
$α$[rad]:位相角(制御角)
この位相角 $α$ を「制御角」といい、$α=0$[rad]のとき、$V_d$ は最大で、$V_d≒0.45$[V]となります。$α=π$[rad]のとき $V_d=0$[V]となります。このことから、$α$ を 0~$π$[rad]の間で変化させることによって、直流電圧 $V_d$ が制御できます。
なお、整流素子として、整流ダイオードを使用した場合は、電源電圧 $v$ が整流ダイオードに順方向電圧として加わったときから電流 $i_d$ が流れますので、直流平均電圧 $V_d$ は式(1)で $α=0$ とした値と等しくなります。
整流ダイオードを使った単相半波整流回路の直流平均電圧を求める式
$V_d≒0.45V$
$V_d$[V]:直流平均電圧
$V$[V]:交流電圧の実効値
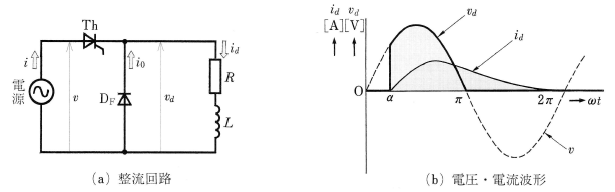
図(c)は誘導性の負荷が接続された場合で、負荷のインダクタンス $L$[H]のために、電流 $i_d$ の立ち上がりが遅れ、電圧 $v_d$[V]の位相が $π$[rad]を超えて、負の半サイクルに入っても $i_d$ は流れ続け、$ωt=π+β$[rad]の時点で 0 Aとなります。そのため、直流電圧 $v_d$ は負の部分が生じ、直流平均電圧 $V_d$ は抵抗負荷の場合より低下してしまいます。そこで、図3のように、負荷と並列にダイオード $D_F$ を接続します。
電源電圧 $v$[V]が正のときは、負荷に流れる電流 $i_d$ は $i$[A]ですが、負になると、ダイオード $D_F$ の回路を通って負荷に環流する電流 $i_o$[A]が生じ、この電流が負荷を流れる電流 $i_d$ となります。このため、図(b)のように、電源電圧 $v$ が負の半サイクルになっても、直流電圧 $v_d$ は負の電圧にならないため、整流特性もよくなります。
このダイオードは「フリーホイーリングダイオード」とよばれ、整流回路のほか、インダクタンスに蓄えられるエネルギーを電流として環流させ、出力電流の脈動を少なくしたり、インダクタンスの悪影響を除去するために使われています。
単相全波整流回路(単相ブリッジ整流回路)
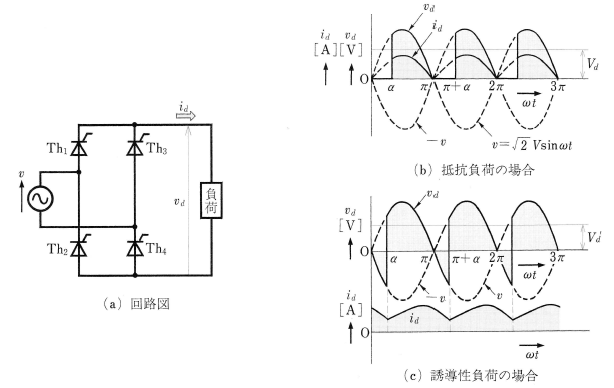
図4(a)は、制御角 $α$[rad]でターンオンするサイリスタの単相ブリッジ整流回路(単相全波整流回路)です。図(b)は、抵抗負荷の場合の電圧と電流の波形で、単相半波整流回路と違って、電源電圧 $v=\sqrt{2}Vsinωt$[V]の位相が $π~2π$[rad]の間でも、制御角 $π+α$[rad]から $2π$[rad]まで、$Th_3$,$Th_2$ によって電流 $i_d$ が流れ、単相半波整流回路の2倍の出力が得られます。したがって、直流平均電圧 $V_d$[V]は次の式で表すことができます。
サイリスタを使った単相全波整流回路の直流平均電圧を求める式
$V_d≒0.9V\displaystyle\frac{1+cosα}{2}$
$V_d$[V]:直流平均電圧
$V$[V]:交流電圧の実効値
$α$[rad]:位相角(制御角)
制御角 $α=0$[rad]で、$V_d=0.9V$[V]と最大になり、$α=π$[rad]で、$V_d=0$[V]となります。なお、整流素子として整流ダイオードを使用した場合、直流平均電圧は、制御角 $α=0$[rad]としたときの $V_d$ に等しくなります。
整流ダイオードを使った単相全波整流回路の直流平均電圧を求める式
$V_d≒0.9V$
$V_d$[V]:直流平均電圧
$V$[V]:交流電圧の実効値
誘導性の負荷の場合、負荷のインダクタンス $L$[H]が大きく、制御角 $α$ が小さいと、図4(c)のように、$L$ の影響を受けて $i_d$ は連続して流れます。このときの直流平均電圧 ${V_d}’$[V]は、
誘導性の負荷を接続した場合のサイリスタを使った単相全波整流回路の直流平均電圧を求める式
${V_d}’≒0.9Vcosα$
${V_d}’$[V]:直流平均電圧
$V$[V]:交流電圧の実効値
$α$[rad]:位相角(制御角)
となります。この場合、制御角 $α=\displaystyle\frac{π}{2}$[rad]で、${V_d}’=0$[V]となり、$α=\displaystyle\frac{π}{2}~π$[rad]では、${V_d}’$ は負になります。
また、負荷のインダクタンス $L$[H]が小さく、制御角 $α$ が大きいときは、出力電流 $i_d$ は断続して流れるようになります。
脈流と平滑コンデンサ
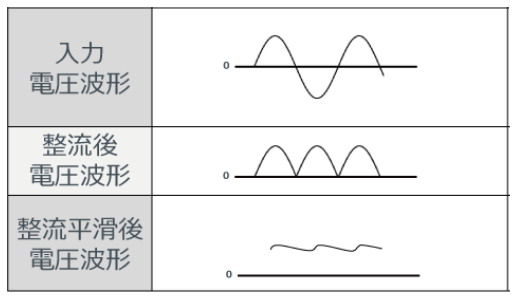
ダイオードを使った全波整流回路の出力波形は、脈流(リプル)といい、脈動した波形になります。整流波形を直流で使う場合、脈流は使い勝手が良くないため、波形をなるべく平らにする必要があります。
そのため 図5(a)のように、コンデンサを回路に入れることにより、波形を平らに近づけることが出来ます。このコンデンサのことを「平滑コンデンサ」といいます。
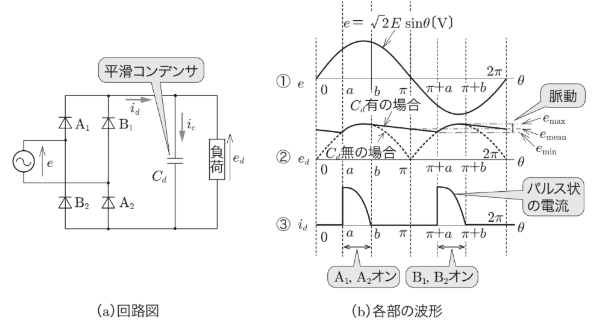
平滑コンデンサは、出力波形の山の部分では充電され、出力波形の谷の部分では電気を放電して負荷に供給し、波形は平滑になります。そのため、コンデンサは一種の電圧源として働いています。なお、コンデンサの静電容量が大きいほど、また負荷電流が少ないほど 脈動は少なくなります(波形が平らになります)。
三相半波整流回路(三相ブリッジ整流回路)
図6(a)は、3個のサイリスタを使った三相半波整流回路で図(b)は電圧波形です。負荷の負側の端子は交流電源の中性点に接続します。
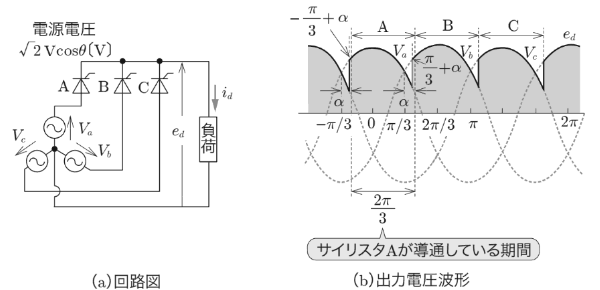
電源の1周期の間に、サイリスタA,B,Cの間で、3回の転流が行われます。三相電源の線間電圧を $v=\sqrt{2}Vsinωt$[V]とすると、直流平均電圧 $V_d$[V]は、次のようになります。
サイリスタを使った三相半波整流回路の直流平均電圧を求める式
$V_d≒1.17V_lcosα$
$V_d$[V]:直流平均電圧
$V_l$[V]:線間電圧の実効値
$α$[rad]:位相角(制御角)
サイリスタのかわりに3個の整流ダイオードを使用した三相全波整流回路の直流平均電圧 $V_d$ は、$α=0$[rad]とおいて求めることができます。
整流ダイオードを使った三相半波整流回路の直流平均電圧を求める式
$V_d≒1.17V_l$
$V_d$[V]:直流平均電圧
$V_l$[V]:線間電圧の実効値
三相全波整流回路(三相ブリッジ整流回路)
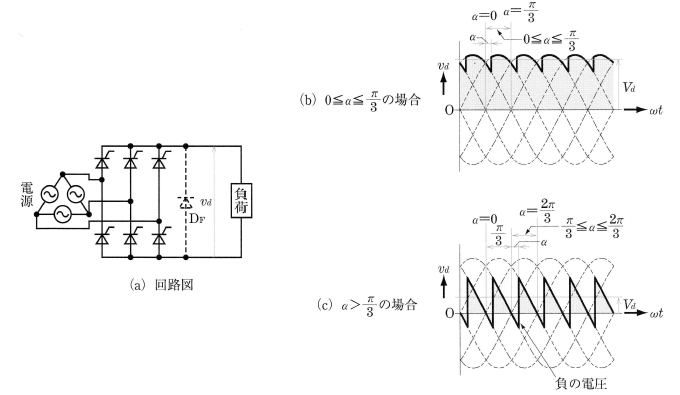
図8(a)は、6個のサイリスタを使った三相ブリッジ整流回路で図(b),(c)は電圧波形です。三相電源の線間電圧を $v=\sqrt{2}Vsinωt$[V]とすると、図(b)のように、直流平均電圧 $V_d$[V]は、$0≦α≦$\displaystyle\frac{π}{3}$[rad]の範囲では次のようになります。
サイリスタを使った三相全波整流回路の直流平均電圧を求める式
$V_d≒1.35V_lcosα$
$V_d$[V]:直流平均電圧
$V_l$[V]:線間電圧の実効値
$α$[rad]:位相角(制御角)
サイリスタのかわりに6個の整流ダイオードを使用した三相全波整流回路の直流平均電圧 $V_d$ は、$α=0$[rad]とおいて求めることができます。
整流ダイオードを使った三相全波整流回路の直流平均電圧を求める式
$V_d≒1.35V_l$
$V_d$[V]:直流平均電圧
$V_l$[V]:線間電圧の実効値
また、図(c)のように、$α$ が $\displaystyle\frac{π}{3}$[rad]の範囲を超えると、直流出力電圧 $v_d$ は負の部分が生じ、負の部分でも、負荷のインダクタンス $L$[H]によって、出力電流は流れ続けます。そして、$α=\displaystyle\frac{π}{3}$[rad]では $v_d$ の大きさは正負同じになり、$V_d$は 0[V]となります。そこで、負荷と並列にフリーホイーリングダイオード $D_F$ を設けると、負の電圧がなくなり、 このときの直流平均電圧 ${V_d}’$[V]は次のようになります。
${V_d}’=1.35V\left\{1+cos\left(α+\displaystyle\frac{π}{3}\right)\right\}$
交流電力調整装置
交流の周波数を変えずに出力電圧を変換する機器に「交流電力調整装置」があります。サイリスタを2つ組み合わせたもので、図9(a)は、サイリスタ(SCR)を用いた交流電力の調整回路の例です。この回路では、図(c)のような「位相制御」といわれる交流電力の制御が行われます。
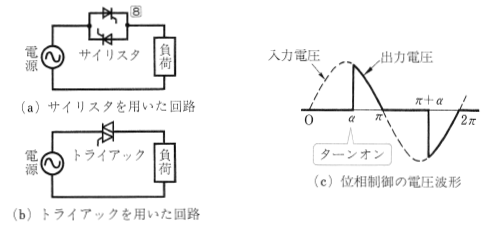
サイリスタをターンオンさせるタイミングを遅くすることにより、出力電圧を下げることができます。波形図の $α$ のことを制御角といい、制御角 $α$ を大きくすれば、出力電圧は小さくなり、制御角 $α$ を小さくすれば、出力電圧は大きくなります。$α= 0$ のとき、出力電圧は入力電圧 (電源電圧) に等しくなります。
電験三種-機械の過去問解説:整流回路の原理
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1999年(平成11年)問5
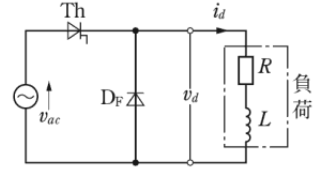
図のようなサイリスタ Th とダイオード $D_F$ を用いた単相半波整流回路がある。この回路で、Th が点弧した後、電源電圧 $V_{ac}$ が正の半サイクルにあって負荷電流 $i_d$が増加中は、負荷のインピーダンス $L$ にエネルギーが蓄えられる。$i_d$ が最大値を過ぎると蓄えられたエネルギーの放出が始まる。$V_{ac}$ が負の半サイクルに入った後は、負荷に蓄えられたエネルギーは $D_F$ を通じて還流する。
この回路の負荷電流 $i_d$ の波形として、正しいのは次のうちどれか。
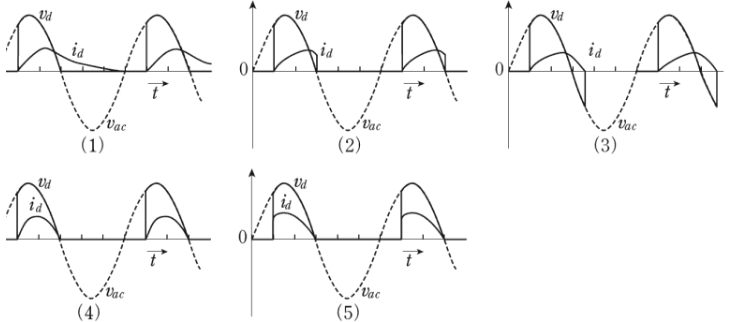
1999年(平成11年)問5 過去問解説
ダイオード $D_F$ はフリーホイーリングダイオードとよばれ、整流回路のほか、インダクタンスに蓄えられるエネルギーを電流として環流させ、出力電流の脈動を少なくしたり、インダクタンスの悪影響を除去するために使われています。

$v_d$ がある規定値の電圧になったところで、点弧(スイッチON)となり、電流が流れ始めます。しかし、負荷に誘導性のコイルがありますので、電流は電圧より遅れます。電流波形が減少の領域に入ると、コイルの逆起電力が環流することによって、電圧波形が負の領域に達して $D_F$ が消弧しても、負荷に電流が流れ続けます。
答え (1)
2003年(平成15年)問9
図1のように、サイリスタを用いた単相ブリッジ接続の変換装置により、誘導性負荷に電力を供給している。図2の $v_d$ 及び $i_d$ は、それぞれ負荷の電圧及び電流の波形である。これに関する記述として、正しいのは次のうちどれか。
ただし、変換装置の位相制御角は $α$ とし、重なり角は無視するものとする。
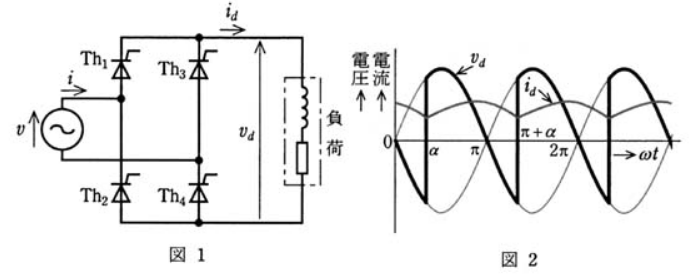
- サイリスタがオン状態にあるためには、必ず正のゲート電流をながさなければならない。
- 直流電流 $i_d$ の方向は $α$ を大きくすると反転する。
- 負荷インダクタンスが大きく、$α$ が小さければ、直流電流 $i_d$ は連続して流れる。
- 直流電流 $i_d$ が連続して流れているとき、交流電圧 $v$ を $v=\sqrt{2}Vsinωt$ とすれば、直流電流 $v_d$ の平均値 $V_d$ は $V_d=\sqrt{2}Vcosα$ となる。
- 直流電流 $i_d$ が完全に平滑であるとすれば、交流電流iは正弦波となる。
2003年(平成15年)問9 過去問解説
- 誤:サイリスタはオンにするときに、ゲートに正の電流を流します。サイリスタをオフにするには、アノード電流がある値以下にします。
- 誤:サイリスタは、電流方向が一定です。
- 正しい記述です。
- 誤:直流電圧の平均値は $V_d=\displaystyle\frac{2}{π}\sqrt{2}Vcosα$ となります。
- 誤:直流電流が完全な平滑であるためには、交流は方形波でなければなりません。
答え (3)
2004年(平成16年)問9
単相整流回路の出力電圧に含まれる主な脈動成分(脈流)の周波数は、半波整流回路では入力周波数と同じであるが、全波整流回路では入力周波数の( ア )倍である。
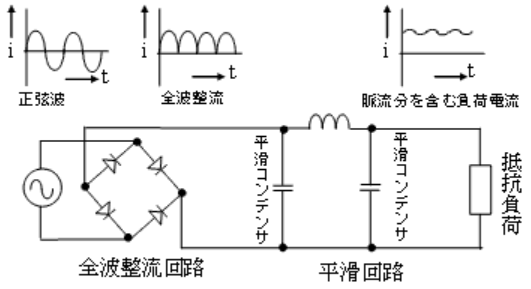
単相整流回路の抵抗負荷を接続したとき、負荷端子間の脈動成分を減らすために、平滑コンデンサを整流回路の出力端子間に挿入する。この場合、その静電容量が( イ )、抵抗負荷電流が( ウ )ほど、コンデンサからの放電が穏やかになり、脈動成分は小さくなる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に記入する語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | $\displaystyle\frac{1}{2}$ | 大きく | 小さい |
| (2) | 2 | 小さく | 大きい |
| (3) | 2 | 大きく | 大きい |
| (4) | $\displaystyle\frac{1}{2}$ | 小さく | 大きい |
| (5) | 2 | 大きく | 小さい |
2004年(平成16年)問9 過去問解説
単相整流回路の出力電圧に含まれる主な脈動成分(脈流)の周波数は、半波整流回路では入力周波数と同じであるが、全波整流回路では入力周波数の( 2 )倍である。
単相整流回路の抵抗負荷を接続したとき、負荷端子間の脈動成分を減らすために、平滑コンデンサを整流回路の出力端子間に挿入する。この場合、その静電容量が( 大きく )、抵抗負荷電流が( 小さい )ほど、コンデンサからの放電が穏やかになり、脈動成分は小さくなる。
平滑回路のコンデンサ容量が大きければ、交流の脈流分を吸収しやすくなり、負荷電流が小さい程、脈流分が少なくなります。
負荷電流がコンデンサのフィルター能力を超すほど大きな電流になると、コンデンサは脈流分を吸収することができずに、負荷抵抗に流れ込むことになります。また、コイルはリップル分の通過阻止の役割をします。
答え (5)
2005年(平成17年)問9
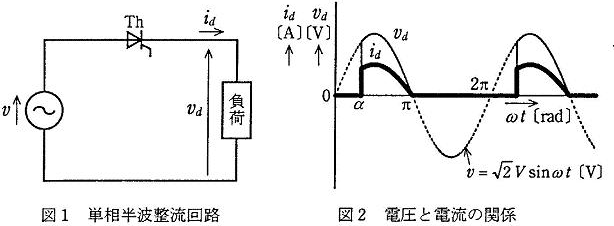
図1は整流素子としてサイリスタを使用した単相半波整流回路で、図2は、図1 において負荷が( ア )の場合の電圧と電流の関係を示す。電源電圧 $v$ が $\sqrt{2}Vsinωt$[V]であるとき、 $ωt$ が 0 から $π$[rad]の間においてサイリスタThを制御角 $α$[rad]でターンオンさせると、電流 $i_d$[A]が流れる。このとき、負荷電圧 $v_d$ の直流平均値 $V_d$[V]は、次式で示される。ただし、サイリスタの順方向電圧降下は無視できるものとする。
$ V_d = 0.450V ×$ ( イ )
したがって、この制御角 $α$ が( ウ )[rad]のときに $V_d$ は最大となる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に記入する語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 抵抗 | $\displaystyle\frac{(1+cosα)}{2}$ | 0 |
| (2) | 誘導性 | (1+cosα) | $\displaystyle\frac{π}{2}$ |
| (3) | 抵抗 | (1-cosα) | 0 |
| (4) | 抵抗 | $\displaystyle\frac{(1-cosα)}{2}$ | $\displaystyle\frac{π}{2}$ |
| (5) | 誘導性 | (1+cosα) | 0 |
2005年(平成17年)問9 過去問解説
図1は整流素子としてサイリスタを使用した単相半波整流回路で、図2は、図1 において負荷が( 抵抗 )の場合の電圧と電流の関係を示す。電源電圧 $v$ が $\sqrt{2}Vsinωt$[V]であるとき、 $ωt$ が 0 から $π$[rad]の間においてサイリスタThを制御角 $α$[rad]でターンオンさせると、電流 $i_d$[A]が流れる。このとき、負荷電圧 $v_d$ の直流平均値 $V_d$[V]は、次式で示される。ただし、サイリスタの順方向電圧降下は無視できるものとする。
$ V_d = 0.450V ×$ ( $\displaystyle\frac{(1+cosα)}{2}$ )
したがって、この制御角 $α$ が( 0 )[rad]のときに $V_d$ は最大となる。
電圧と電流が同相ですので、供給負荷は抵抗です。負荷電流の直流平均値 $V_d$ は、
$V_d=\displaystyle\frac{\sqrt{2}V}{π}×\displaystyle\frac{1+cosα}{2}≒ 0.450V ×\displaystyle\frac{(1+cosα)}{2}$
$α=0$ のとき、$V_d$ は、最大になります。
答え (1)
2006年(平成18年)問9
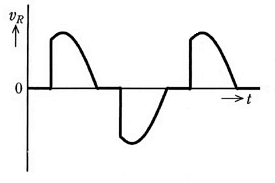
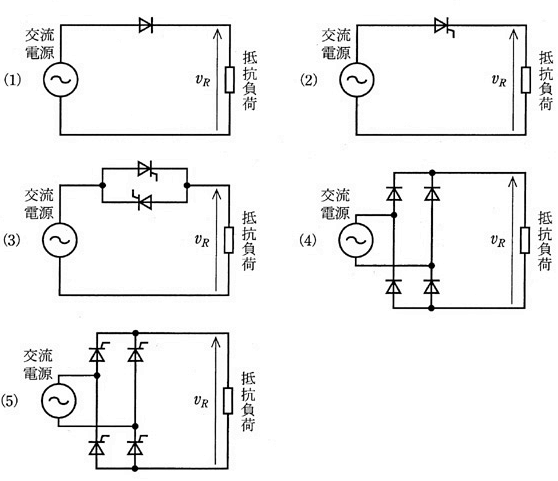
図に示す出力電圧波形 $V_R$ を得ることができる電力変換回路として、正しいのはつぎのうちどれか。
ただし、回路中の交流電源は正弦波交流電圧源とする。
2006年(平成18年)問9 過去問解説
題意の波形図はサイリスタを用いた出力です。全波整流ではないので、(3)が該当します。

答え (3)
2007年(平成19年)問9
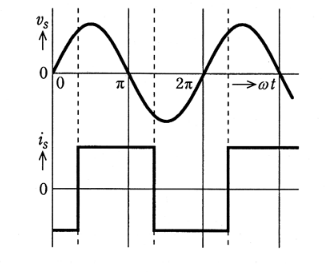
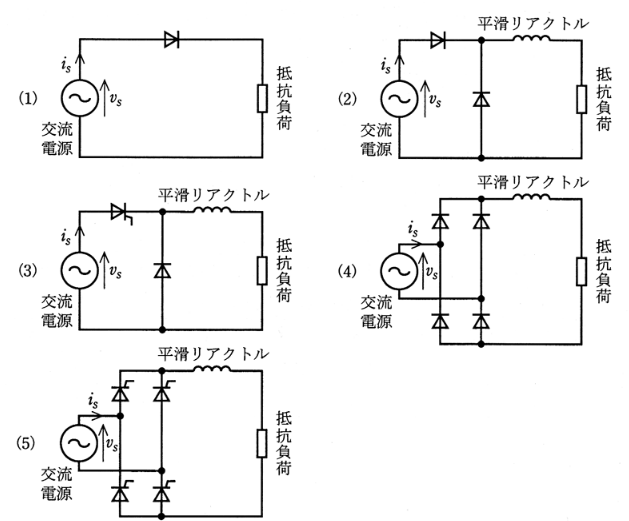
入力交流電圧波 $V_s$ に対し、図のような入力電流波形 $I_s$ となる電力変換回路として、正しいのは次のうちどれか。
ただし、交流電源のインピーダンスは無視できるものとし、電力変換回路における平滑リアクトルは十分に大きなインダクタンスを持っているものとする。
2007年(平成19年)問9 過去問解説
交流電源 $v_s$ に対してずれた位相で電流が上下に流れているので、全波整流のサイリスタタイプとなります。(1)の回路は抵抗のみによる半波整流回路です。残りの4つは平滑リアクトル回路を持っているので電流は一定に保たれます。しかし,(2),(3)の回路は半波整流回路なので一方向のみの電流しか出力されません。(4),(5)はブリッジ整流回路で正負交互に電流は流れますが、出力波形は位相制御がされているますので、サイリスタ素子を使ったものが正解となります。
答え (5)
2007年(平成19年)問16
図は、2個のサイリスタを逆並列に接続し、位相制御により負荷電力を制御する回路を示す。次の(a)及び(b)に答えよ。
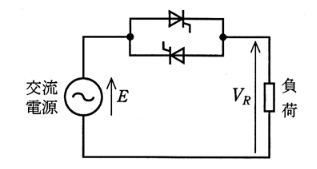
(a) 負荷が抵抗負荷であるとき、制御角 $α$ が 90[°]のときの発熱量は、30[°]のときの発熱量の何倍か。最も近い値は次のうちどれか。
ただし、負荷の抵抗値は一定とする。また、制御角 $α$[rad]のときの負荷電圧の実効値 $V_R$ は、電源電圧の実効値を $E$ とすると、$V_R=E・\sqrt{1-\displaystyle\frac{α}{π}+\displaystyle\frac{sin2α}{2π}}$ で与えられるものとする。
(1) 0.515 (2) 0.717 (3) 0.866 (4) 0.912 (5)0.986
(b) 負荷が抵抗値 $R$[Ω],インダクタンス $L$[H]との直列回路からなる誘導性負荷である場合の記述として、誤っているのは次のうちどれか。ただし、電源の角周波数を $ω$[rad/s]とし、負荷の基本波力率角を $φ=tan^{-1} \displaystyle\frac{ωL}{R}$ とする。
- 定常運転時に $α< φ$ としたとき、サイリスタにオン指令を与えてもサイリスタを毎サイクルターンオン制御できない。
- 負荷が純インダクタンスとみなされる場合は、サイリスタ制御リアクトル方式無効電力補償装置(TCR)と呼ばれ、図の回路を一相分として、無効電力補償装置に使用される。
- 電流の通流幅は、制御角 $α$ と基本波力率角 $φ$ の関数になる。
- 負荷の基本波力率角(遅れ)が大きくなるほどターンオフ直後のサイリスタに印加される電圧の絶対値は小さくなる。
- 電流高調波成分は、第3次成分が最も大きい。
2007年(平成19年)問16 過去問解説
(a) 負荷が抵抗負荷であるとき、制御角 $α$ が 90[°]のときの負荷電圧の実効値 $V_{90}$、30[°]のときの負荷電圧の実効値 $V_{30}$ とすると、
$\begin{eqnarray}V_{90}&=&E・\displaystyle\sqrt{1-\displaystyle\frac{α}{π}+\displaystyle\frac{sin2α}{2π}}\\\\&=&E・\displaystyle\sqrt{1-\displaystyle\frac{\displaystyle\frac{π}{2}}{π}+\displaystyle\frac{sinπ}{2π}}\\\\&=&\displaystyle\frac{E}{\sqrt{2}}\end{eqnarray}$
$\begin{eqnarray}V_{30}&=&E・\displaystyle\sqrt{1-\displaystyle\frac{α}{π}+\displaystyle\frac{sin2α}{2π}}\\\\&=&E・\displaystyle\sqrt{1-\displaystyle\frac{\displaystyle\frac{π}{6}}{π}+\displaystyle\frac{sin\displaystyle\frac{π}{3}}{2π}}\\\\&=&E・\displaystyle\sqrt{\displaystyle\frac{5}{6}+\displaystyle\frac{\sqrt{3}}{4π}}\end{eqnarray}$
抵抗で発生する熱量は、$\displaystyle\frac{V^2}{R}$ ですので、電圧の実効値の2乗に比例します。したがって、
$\left(\displaystyle\frac{V_{90}}{V_{30}}\right)^2=\displaystyle\frac{\displaystyle\frac{1}{2}}{\displaystyle\frac{5}{6}+\displaystyle\frac{\sqrt{3}}{4π}}≒0.515$
答え (1)
(b) サイリスタを逆並列に接続し、位相制御を行うことにより負荷電力を制御できます。この回路を一つの素子にしたものがトライアックまたは双方向サイリスタです。電流の通流幅は、制御角 $α$ と基本波力率角 $φ$ の関数になります。基本波力率角は基本周波数(交流電源の周波数)における力率角です。負荷が純インダクタンスの場合は、サイリスタ制御リアクトル方式無効電力補償装置(TCR)となります。
- 正しい記述です。
- 正しい記述です。
- 正しい記述です。
- 誤:負荷の基本波力率角(遅れ)が大きくなるほどターンオフ直後のサイリスタに印加される電圧の絶対値は大きくなります。
- 正しい記述です。
答え (4)
2010年(平成22年)問16
図には、バルブデバイスとしてサイリスタを用いた単相全波整流回路を示す。交流電源電圧を $e=\sqrt{2}Esinωt$[V]、単相全波整流回路出力の直流電圧を $e_d$[V]、サイリスタの電流を $i_T$[A]として、次の(a)及び(b)に答えよ。
ただし、重なり角などは無視し、平滑リアクトルにより直流電流は一定とする。
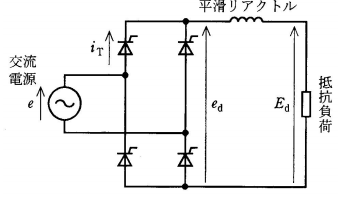
(a) サイリスタの制御遅れ角 $α$ が $\displaystyle\frac{π}{3}$[rad]のときに、$e$ に対する、$e_d$,$i_T$ の波形として、正しいのは次のうちどれか。
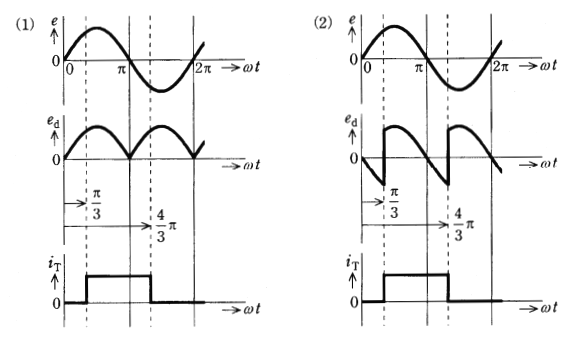
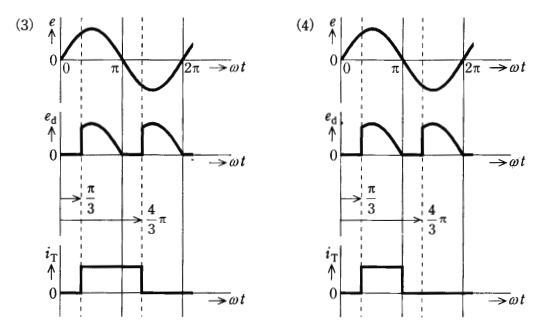
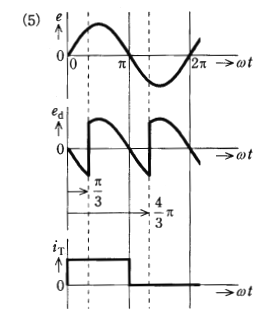
(b) 負荷抵抗にかかる出力の直流電圧 $E_d$[V]は上記(a)に示された瞬時値波形の平均値となる。制御遅れ角 $α$ を $\displaystyle\frac{π}{2}$[rad]としたときの電圧[V]の値として、正しいのは次のうちどれか。
(1) 0 (2) $\displaystyle\frac{\sqrt{2}}{π}E$ (3) $\displaystyle\frac{1}{2}E$ (4) $\displaystyle\frac{\sqrt{2}}{2}E$ (5) $\displaystyle\frac{2\sqrt{2}}{π}E$
2010年(平成22年)問16 過去問解説
(a) 設問の回路は、単相全波整流回路です。サイリスタの制御遅れ角が $α=\displaystyle\frac{π}{3}$[rad]のときの、電源電圧 $e$ に対する、負荷に加わる電圧 $e_d$,サイリスタに流れる電流 $i_T$ の波形を示します。平滑リアクトルが接続された負荷の場合、電圧が 0[V]でも電流は流れます。
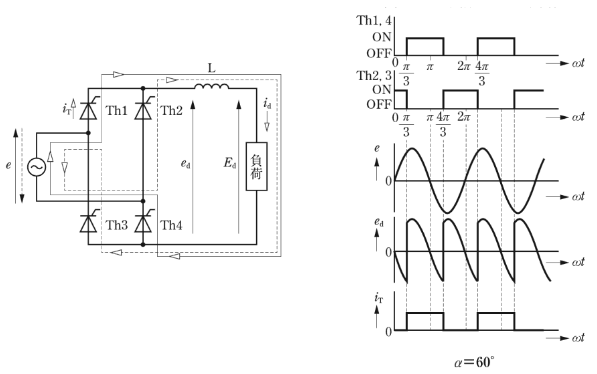
答え (2)
(b) 負荷が誘導性のときの直流平均電圧 $E_d$[V]は、
$E_d≒0.9Ecosα$
制御角 $α=\displaystyle\frac{π}{2}$[rad]で、$E_d=0$[V]となります。
答え (1)
2011年(平成23年)問9
次の文章は、単相双方向サイリスタスイッチに関する記述である。
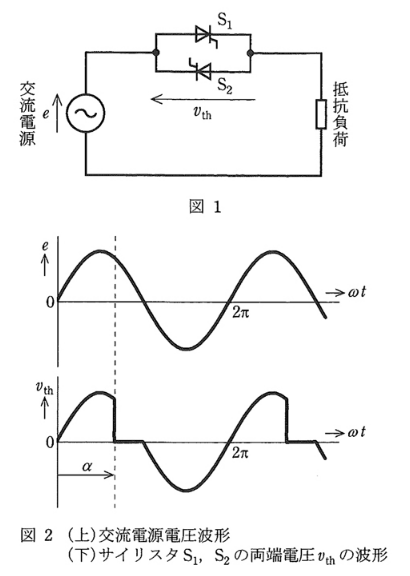
図1は、交流電源と抵抗負荷との間にサイリスタ $S_1$,$S_2$ で構成された単相双方向スイッチを挿入した回路を示す。図示する電圧の方向を正とし、サイリスタの両端にかかる電圧 $v_{th}$ が図 2(下)の波形であった。
サイリスタ $S_1$,$S_2$ の運転として、このような波形となりえるものを次の(1)~(5)のうちから一つ選べ。
- $S_1$,$S_2$ とも制御遅れ角 $α$ で運転
- $S_1$ は制御遅れ角 $α$,$S_2$ は制御角 0 で運転
- $S_1$ は制御遅れ角 $α$,$S_2$ はサイリスタをトリガ(点弧)しないで運転
- $S_1$ は制御遅れ角 0,$S_2$ は制御遅れ角 $α$ で運転
- $S_1$ はサイリスタをトリガ(点弧)しないで,$S_2$ は制御遅れ角 $α$ で運転
2011年(平成23年)問9 過去問解説
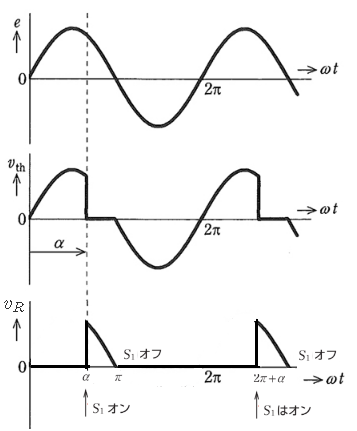
負荷の電圧を $v_R$ とすると、電源電圧 $e$ の波形は、サイリスタの電圧の波形 $v_{th}$ +負荷電圧の波形 $v_$ です。
負荷に正の電圧が加わる、$α$ と $2π+α$ で $S_1$ はオンします。制御遅れ角は、$α$ です。 サイリスタの電圧で、負側は常に印加されています。これは、負荷にマイナスの電圧が印加されない、つまりサイリスタ $S_2$ はオン(点弧)しないことを意味しています。
したがって、(3)が正解になります。
答え (3)
2011年(平成23年)問17
次の図は、バルブデバイスとしてダイオードを用いた三相整流装置の回路を示す。
平滑リアクトルのインダクタンス $L_d$[H]は十分に大きく、直流電流 $I_d $[A]は一定になっているものとする。
交流側にリアクタンス $X$[Ω]のリアクトルがあると転流時に重なり角が生じ、直流電圧が降下する。また、ダイオードの順電圧降下 $V_F$[V]によっても直流電圧が降下する。これら以外の電圧降下は無視する。入力交流電圧が $V_L$[V]のときのこの整流装置の出力電圧 $V_d$[V]は次式で求められる。
$V_d=\displaystyle\frac{3\sqrt{2}}{π}V_L-\displaystyle\frac{3}{π}X・I_d-2V_F$
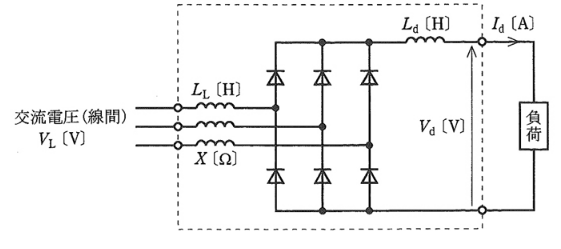
この整流装置の入力交流電圧は $V_L=200$[V],周波数は $f=50$[Hz]で、電機子電流は $I_d=36$[A]である。 交流側のリアクトルのインダクタンスは $L_L=5.56×10^{-4}$[H]で、その抵抗値は平滑リアクトルの抵抗値とともに無視できるものとする。また、各ダイオードの順電圧降下は $V_F=1.0$[V]で一定とする。次の(a)及び(b)の問に答えよ。
(a) ダイオードでは、電流の通電によって損失が発生する。一つのダイオードで発生する損失の平均値は、通電する期間が1サイクルの$\displaystyle\frac{1}{3}$であるとして計算できる。一つのダイオードで発生する損失[W]の平均値に最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 12 (2) 18 (3) 24 (4) 36 (5) 72
(b) 出力電圧 $V_d$[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 251 (2) 262 (3) 263 (4) 264 (5) 270
2011年(平成23年)問17 過去問解説
(a) 一つのダイオードの損失を $p$[W]とすると、
$p=V_FI_d$
一つのダイオードで発生する損失の平均値は、通電する期間が1サイクルの$\displaystyle\frac{1}{3}$であるとして計算できるとありますので、一つのダイオードで発生する損失の平均値 $p_a$[W]は、
$p_a=\displaystyle\frac{p}{3}=\displaystyle\frac{1.0×36}{3}=12$[W]
答え (1)
(b) $X=2πfL_L$ ですので、出力電圧 $V_d$[V]は、
$\begin{eqnarray}V_d&=&\displaystyle\frac{3\sqrt{2}}{π}V_L-\displaystyle\frac{3}{π}X・I_d-2V_F\\\\&=&\displaystyle\frac{3\sqrt{2}}{π}×200-\displaystyle\frac{3}{π}×2π×50×5.56×10^{-4}×36-2×1\\\\&=&262[V]\end{eqnarray}$
答え (2)
2012年(平成24年)問10
交流電圧 $v_a$[V]の実効値 $V_a$[V]が 100[V]で、抵抗負荷が接続された図1に示す半導体電力変換装置において、図2に示すようにラジアンで表した制御遅れ角 $α$[rad]を変えて出力直流電圧 $v_d$[V]の平均値 $V_d$[V]を制御する。
度数で表した制御遅れ角 $α$[°]に対する $V_d$[V]の関係として、適切なものを次の(1)~(5)のうちから一つ選べ。
ただし、サイリスタの電圧降下は、無視する。
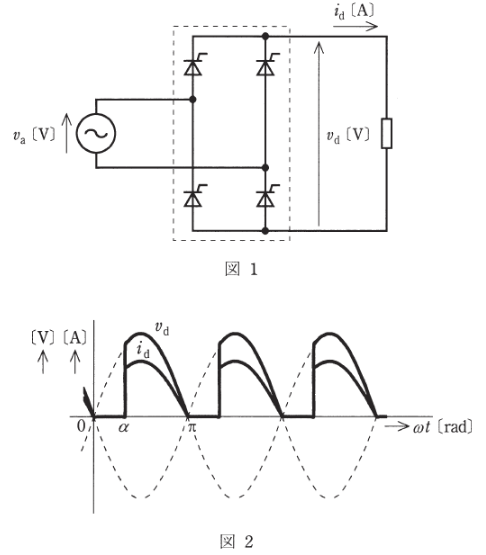
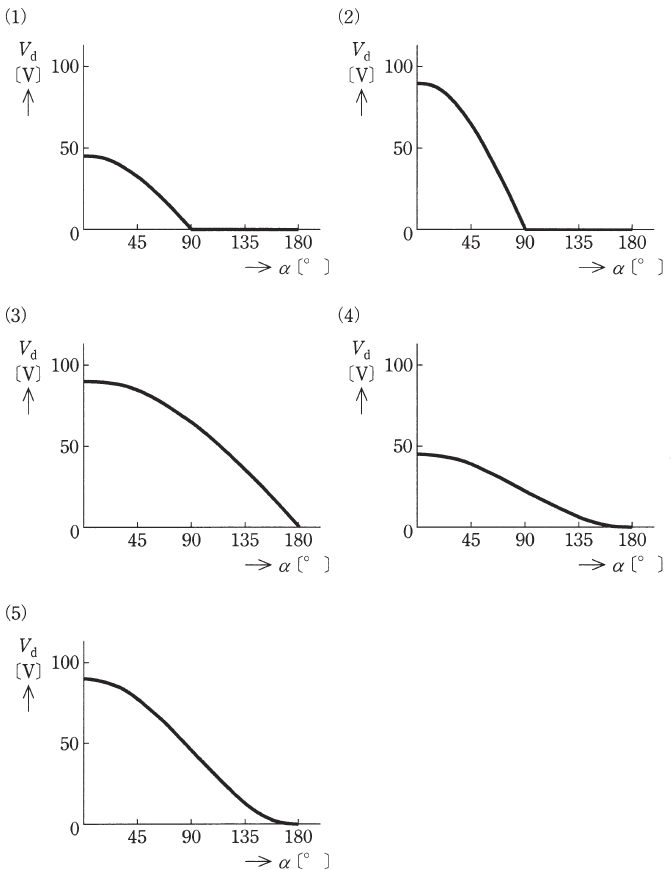
2012年(平成24年)問10 過去問解説
図1は、単相ブリッジ整流回路です。直流平均電圧 $V_d$[V]は、
$V_d≒0.9V_a\displaystyle\frac{1+cosα}{2}=90×\displaystyle\frac{1+cosα}{2}$
$α=0,90,180$[°]を代入すると、$V_d=90,45,0$[V]となります。したがって、(5)が正解となります。
答え (5)
2013年(平成25年)問9
次の文章は、下図に示すような平滑コンデンサをもつ単相ダイオードブリッジ整流回路に関する記述である。
図の回路において、平滑コンデンサの電流 $i_C$ は、交流電流 $i_s$ を整流した電流と負荷に供給する電流 $i_d$ との差となり、電圧 $v_d$ は( ア )波形となる。この平滑コンデンサをもつ整流回路は、負荷側からみると直流の( イ )として動作する。
交流電源は、負荷インピーダンスに比べ電源インピーダンスが非常に小さいことが一般的であるので、通常の用途では交流の( ウ )として扱われる。この回路の交流電流 $i_s$ は、正負の( エ )波形となる。これに対して、図には示していないが、リアクトルを交流電源と整流回路との間に挿入するなどして、波形を改善することが多い。
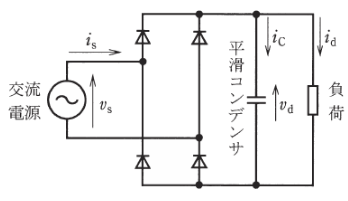
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 脈動する | 電圧源 | 電圧源 | パルス状の |
| (2) | 正負に反転する | 電流源 | 電圧源 | パルス状の |
| (3) | 脈動する | 電圧源 | 電圧源 | ほぼ方形波の |
| (4) | 正負に反転する | 電圧源 | 電流源 | パルス状の |
| (5) | 正負に反転する | 電流源 | 電流源 | ほぼ方形波の |
2013年(平成25年)問9 過去問解説
図の回路において、平滑コンデンサの電流 $i_C$ は、交流電流 $i_s$ を整流した電流と負荷に供給する電流 $i_d$ との差となり、電圧 $v_d$ は( 脈動する )波形となる。この平滑コンデンサをもつ整流回路は、負荷側からみると直流の( 電圧源 )として動作する。
交流電源は、負荷インピーダンスに比べ電源インピーダンスが非常に小さいことが一般的であるので、通常の用途では交流の( 電圧源 )として扱われる。この回路の交流電流 $i_s$ は、正負の( パルス状の )波形となる。これに対して、図には示していないが、リアクトルを交流電源と整流回路との間に挿入するなどして、波形を改善することが多い。
ダイオードを用いた単相ブリッジ整流回路の出力電圧は、抵抗負荷の場合は、半周期ごとに 0[V]が現れる脈動する波形となります。この直流電圧の脈動を吸収するために、負荷と並列にコンデンサを接続します。このコンデンサを平滑コンデンサといいます。
供給される交流電流は平滑コンデンサを充電するときに正負のパルス状の波形となり、高調波を生じまので、低減するためにリアクトルなどを挿入します。
答え (1)
2014年(平成26年)問10
次の文章は、単相半波ダイオード整流回路に関する記述である。
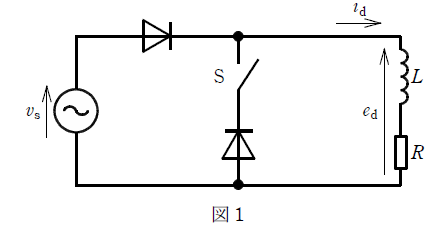
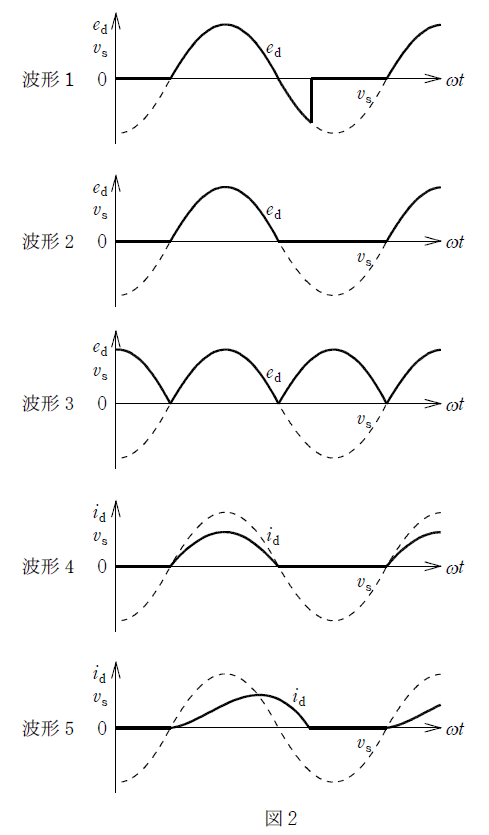
抵抗とリアクトルとを直列接続した負荷に電力を供給する単相半波ダイオード整流回路を図1に示す。スイッチSを開いて運転したときに、負荷力率に応じて負荷電圧 $e_d$ の波形は図2の( ア )となり、負荷電流 $i_d$ の波形は図2の( イ )となった。次にスイッチSを閉じ、環流ダイオードを接続して運転したときには、負荷電圧 $e_d$ の波形は図2の( ウ )となり、負荷電流の流れる期間は、スイッチSを開いて運転したときよりも( エ )。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 波形2 | 波形4 | 波形3 | 長くなる |
| (2) | 波形1 | 波形5 | 波形2 | 長くなる |
| (3) | 波形1 | 波形5 | 波形3 | 短くなる |
| (4) | 波形1 | 波形4 | 波形2 | 長くなる |
| (5) | 波形2 | 波形5 | 波形3 | 短くなる |
2014年(平成26年)問10 過去問解説
抵抗とリアクトルとを直列接続した負荷に電力を供給する単相半波ダイオード整流回路を図1に示す。スイッチSを開いて運転したときに、負荷力率に応じて負荷電圧 $e_d$ の波形は図2の( 波形1 )となり、負荷電流 $i_d$ の波形は図2の( 波形5 )となった。次にスイッチSを閉じ、環流ダイオードを接続して運転したときには、負荷電圧 $e_d$ の波形は図2の( 波形2 )となり、負荷電流の流れる期間は、スイッチSを開いて運転したときよりも( 長くなる )。
負荷にあるリアクトルは、負荷電圧 $e_d$ が0になっても、蓄えたエネルギーで電流を流します。そのため負荷電流 $i_d$ はすぐに 0 にはなりません。
Sの下にあるダイオードは、フリーホイーリングダイオードとして働きます。これは、インダクタンスに蓄えられるエネルギーを電流として環流させ、出力電流の脈動を少なくしたり、インダクタンスの悪影響を除去するために使われています。Sを閉じることによって、負荷電流の流れる期間は、長くなります
答え (2)
2016年(平成28年)問16
純抵抗を負荷とした単相サイリスタ全波整流回路の動作について、次の(a)及び(b)の問に答えよ。
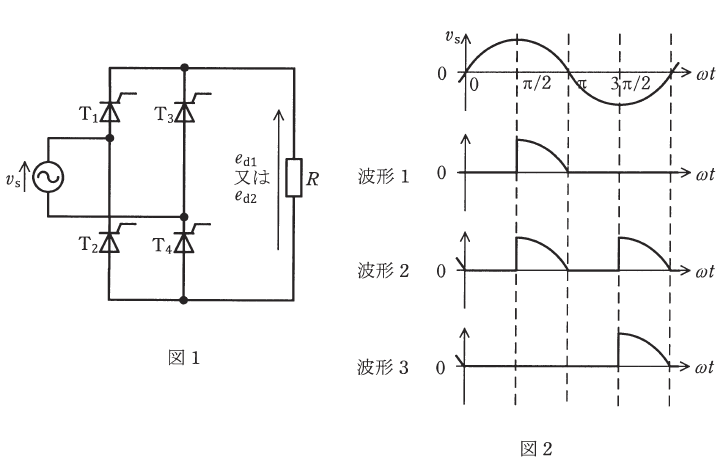
(a) 図1に単相サイリスタ全波整流回路を示す。サイリスタ $T_1~T_4$ に制御遅れ角 $α=\displaystyle\frac{π}{2}$[rad]で、ゲート信号を与えて運転しようとしている。$T_2$及び$T_3$のゲート信号は正しく与えられたが、$T_1$及び$T_4$のゲート信号が全く与えられなかった場合の出力電圧波形を$e_{d1}$とし、正しく$T_1~T_4$にゲート信号が与えられた場合の出力電圧波形を$e_{d2}$とする。図2の波形1~波形3から、$e_{d1}$と$e_{d2}$の組合せとして正しいものを次の(1)~(5)のうちから一つ選べ。
| 電圧波形 $e_{d1}$ | 電圧波形 $e_{d2}$ | |
| (1) | 波形1 | 波形2 |
| (2) | 波形2 | 波形1 |
| (3) | 波形2 | 波形3 |
| (4) | 波形3 | 波形1 |
| (5) | 波形3 | 波形2 |
(b) 単相交流電源電圧vsの実効値を $V$[V]とする。ゲート信号が正しく与えられた場合の出力電圧波形 $e_{d2}$ について、制御遅れ角 $α$[rad]と出力電圧の平均値 $E_d$[V]との関係を表す式として、正しいものに最も近いものを次の(1)~(5)のうちから一つ選べ。
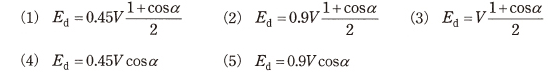
2016年(平成28年)問16 過去問解説
(a) サイリスタは、ゲート信号が与えられる前は電流が流れず、交流電力の位相角 $α$ でゲート信号を加えてターンオンして電流を流します。ここで、$T_1$及び$T_4$のゲート信号が与えられないということは、$T_1$と$T_4$は取り去って考えることができます。
$T_1$と$T_4$を取り去った回路では、電源から負荷に対してサイリスタが2個入った回路になります。このとき、サイリスタの向きを考えると、電源電圧 $v_s$ が+の時はサイリスタが逆方向になりますので、電流は流れません。$v_s$ が‐の時はサイリスタは電流を流します。サイリスタにゲート信号が与えられるのは、制御遅れ角 $α=\displaystyle\frac{π}{2}$[rad]ですので、波形は3になります。
サイリスタ $T_1~T_4$ が正しくゲート信号が与えられた場合は、全てのサイリスタが動作しますので、電源電圧 $v_s$ が+の時は、$T_1$と$T_4$にゲート信号が与えられ、$v_s$ が-の時は、$T_2$と$T_3$にゲート信号が与えられます。制御遅れ角 $α=\displaystyle\frac{π}{2}$[rad]ですので、波形は2になります。
答え (5)
(b) 単相ブリッジ整流回路の出力電圧の平均値 $E_d$[V]は、
$E_d≒0.9V\displaystyle\frac{1+cosα}{2}$
答え (2)
2017年(平成29年)問11
図1は、平滑コンデンサをもつ単相ダイオードブリッジ整流器の基本回路である。なお、この回路のままでは電流波形に高調波が多く含まれるので、実用化に当たっては注意が必要である。
図1の基本回路において、一定の角周波数ωの交流電源電圧をvs、電源電流を $i_1$、図中のダイオードの電流を $i_2$,$i_3$,$i_4$,$i_5$ とする。平滑コンデンサの静電容量は、負荷抵抗の値とで決まる時定数が電源の1周期に対して十分に大きくなるように選ばれている。図2は交流電源電圧vsに対する各部の電流波形の候補を示している。図1の電流 $i_1$,$i_2$,$i_3$,$i_4$,$i_5$ の波形として正しい組合せを次の(1)~(5)のうちから一つ選べ。
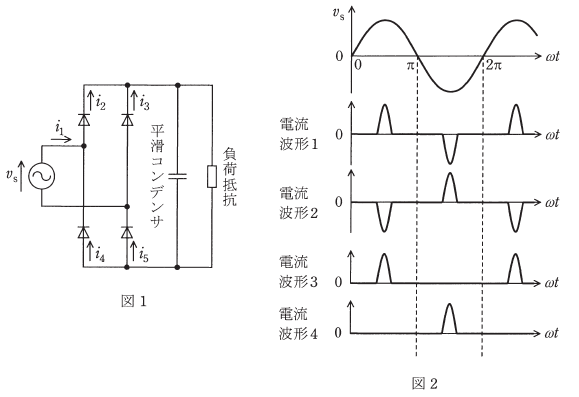
| $i_1$ | $i_2$ | $i_3$ | $i_4$ | $i_5$ | |
| (1) | 電流波形1 | 電流波形4 | 電流波形3 | 電流波形3 | 電流波形4 |
| (2) | 電流波形2 | 電流波形3 | 電流波形4 | 電流波形4 | 電流波形3 |
| (3) | 電流波形1 | 電流波形4 | 電流波形3 | 電流波形4 | 電流波形3 |
| (4) | 電流波形2 | 電流波形4 | 電流波形3 | 電流波形3 | 電流波形4 |
| (5) | 電流波形1 | 電流波形3 | 電流波形4 | 電流波形4 | 電流波形3 |
2017年(平成29年)問11 過去問解説
ダイオードは、順方向は電流を流し、逆方向は電流を流しません。交流電源電圧 vs が正のときの電流 $ i_1$ は、
ダイオード $i_2$ →平滑コンデンサ→ダイオード $i_5$
の順に流れます。つまり、$i_2$ と $i_5$ は同じ波形で正の波形となります。該当するのは3です。
電源電圧 vs が負のときの電流 $-i_1$ は、
ダイオード $i_3$ → 平滑コンデンサ → ダイオード $i_4$
の順に流れます。つまり、$i_3$ と $i_4$ は同じ波形で電圧と逆方向の波形となります。該当するのは4です。このときの、$i_1$ は、4を反転させた波形になります。
したがって、 $i_1$ 全体としては、波形1が該当します。
答え (5)
2017年(平成29年)問16
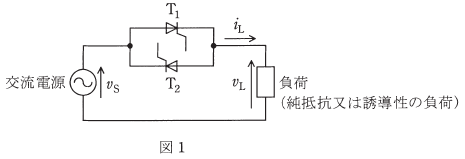
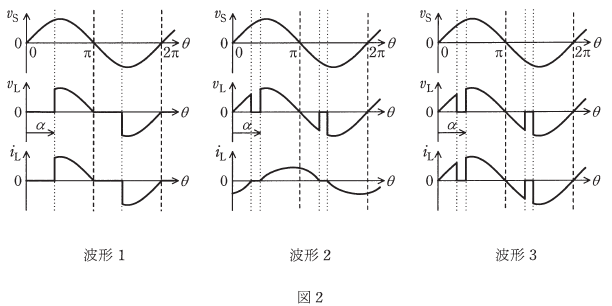
図1に示す単相交流電力調整回路が制御遅れ角 $α$[rad]で運転しているときの動作を考える。
正弦波の交流電源電圧は $v_S$、負荷は純抵抗負荷又は誘導性負荷であり、負荷電圧を $v_L$、負荷電流を $i_L$ とする。次の(a)及び(b)の問に答えよ。
(a) 図2の波形1~3のうち、純抵抗負荷の場合と誘導性負荷の場合とで発生する波形の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| 純抵抗負荷 | 誘導性負荷 | |
| (1) | 波形1 | 波形2 |
| (2) | 波形1 | 波形3 |
| (3) | 波形2 | 波形1 |
| (4) | 波形2 | 波形3 |
| (5) | 波形3 | 波形2 |
(b) 交流電源電圧 $v_S$ の実効値を $V_S$ として、純抵抗負荷の場合の負荷電圧 $v_L$ の実効値 $V_L$は、 $V_L=V_S\displaystyle\sqrt{1-\displaystyle\frac{α}{π}+\displaystyle\frac{sin2α}{2π}}$ で表される。制御遅れ角を $α_1=\displaystyle\frac{π}{2}$[rad]から $α_2=\displaystyle\frac{π}{4}$[rad]に変えたときに、負荷の抵抗で消費される交流電力は何倍となるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.550 (2) 0.742 (3) 1.35 (4) 1.82 (5) 2.00
2017年(平成29年)問16 過去問解説
(a) 純抵抗負荷の場合を考えます。純抵抗負荷とは、抵抗のみの負荷のことで位相の遅れはありません。制御遅れ角 $α$ でゲート信号を加えてターンオンさせると、
0≦θ≦α ではターンオンしていないので、 vL=0
α≦θ≦π では vL=vS(αでターンオン、πでターンオフ)
π≦θ≦π+α ではターンオンしていないので vL=0()
π+α≦θ≦2π vL=vS(π+αでターンオン、2πでターンオフ)
また、iL は vL に追従しますので、波形1が当てはまります。
誘導性負荷の場合を考えます。制御遅れ角 $α$ でゲート信号を加えてターンオンさせると、電圧が印加され、インダクタンスにエネルギーが蓄積され、電流値は徐々に上昇します。また、ターンオフさせると、インダクタンスに蓄積されたエネルギーを放出し、電流値は徐々に0に近づきます。つまり、波形2が当てはまります。
答え (1)
(b) 負荷で諸費される電力は、$P=\displaystyle\frac{V^2}{R}$ ですので、制御遅れ角 $α_1=\displaystyle\frac{π}{2}$[rad] のときの消費電力を $P_1$、制御遅れ角 $α_2=\displaystyle\frac{π}{4}$[rad]のときの消費電力を $P_2$ とすると、
$\displaystyle\frac{P_2}{P_1}=\displaystyle\frac{\displaystyle\frac{{V_{L2}}^2}{R}}{\displaystyle\frac{{V_{L1}}^2}{R}}=\displaystyle\frac{{V_{L2}}^2}{{V_{L1}}^2}$
$=\displaystyle\frac{V_S^2×\displaystyle\left(1-\displaystyle\frac{α_2}{π}+\displaystyle\frac{sin2α_2}{2π}\right)}{V_S^2×\displaystyle\left(1-\displaystyle\frac{α_1}{π}+\displaystyle\frac{sin2α_1}{2π}\right)}$
$=\displaystyle\frac{\displaystyle\left(1-\displaystyle\frac{\frac{π}{4}}{π}+\displaystyle\frac{sin2×\frac{π}{4}}{2π}\right)}{\displaystyle\left(1-\displaystyle\frac{\frac{π}{2}}{π}+\displaystyle\frac{sin2×\frac{π}{2}}{2π}\right)}$
$=\displaystyle\frac{1-\frac{1}{4}+\frac{1}{2π}}{1-\frac{1}{2}+\frac{0}{2π}}≒1.82$
答え (4)
電験三種の機械科目に出題される「パワーエレクトロ二クス」のページ
- パワーエレクトロニクスと半導体デバイス
- 整流回路の原理(整流ダイオードとサイリスタ)
- 直流チョッパとその応用
- インバータの動作原理とその応用






