第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「電気分解とファラデーの法則」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「電気分解とファラデーの法則」の過去問題も解説しています。
電解質と電気分解
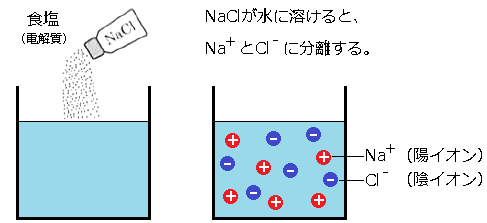
電荷を帯びた原子を「イオン」といいます。たとえば食塩(NaCl)を水に溶かすとプラスの電荷をもったナトリウムイオン(Na+)と、マイナスの電荷をもった塩素イオン(Cl–)に分離します。
このように水に溶かすとイオンに分離する物質を「電解質」といい、電解質の溶液を「電解液」といいます。また、プラスの電荷をもつイオンを「陽イオン」、マイナスの電荷をもつイオンを「陰イオン」といいます。塩化ナトリウム(NaCl)や塩酸(HCl),水酸化ナトリウム(NaOH)などは、陽イオンと陰イオンが静電気力で結合してできている物質です。このような物質を、「イオン結合性物質」といいます。
電解液のなかに電極を入れて電極をつなぐと陽イオンは陰極(-)へ、陰イオンは陽極(+)へ引き寄せられ、電流が流れます。
食塩水は電気を通しますが、砂糖水やアルコール水は電気を通しません。これは、砂糖やアルコールは水に溶かしてもイオンに分離しないためです。このような物質を非電解物質といいます。
- 電解質:食塩(塩化ナトリウム)、硫酸、塩酸など
- 非電解質:砂糖、アルコール、水銀など
電気分解
電気分解とは、電解質の溶液に電極を差し込み電流を流すと、電極と溶液の間で酸化還元反応が起きて、電解質が分解される現象です。
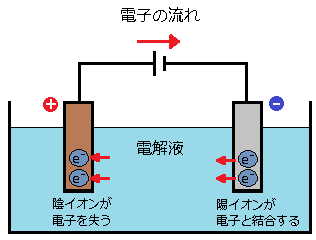
イオンは原子から電子が抜き取られたり、余分にくっついたりしてできたものです。そのため電解液のなかに電極を入れて電流を流すと、陽極と陰極の周囲で次のような化学反応が起こります。
- 陽極:引き寄せられた陰イオンが電子を放出する
- 陰極:引き寄せられた陽イオンが電子と結合する
この結果電極の周囲には何らかの物質が析出します。この一連の操作を「電気分解」といいます。
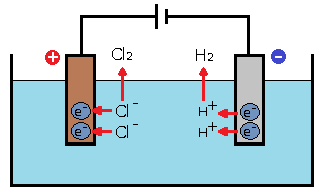
たとえば塩酸(HCl)溶液を電気分解すると両極ではそれぞれ次のような反応が起こります。
陽極:塩素イオン(Cl– )が電子を失って塩素原子になり、2個結合して塩素分子(Cl2 )を析出。
2Cl–(塩素イオン)→ Cl2(塩素)+ 2e–(電子)
陰極:水素イオン(H+)が電子と結合して水素原子になり、2個結合して水素分子(H2)を析出。
2H+(水素イオン)+ 2e–(電子)→ H2(水素)
電気分解は次のような工業分野で利用されています。
- 化学物質の製造
苛性ソーダ(NaOH)、塩素(Cl)などを電気分解で析出する。
- 金属の電解精錬
不純物を含む金属を水溶液から電気分解によって析出する(銅、亜鉛、ニッケルなど)。
- 溶融塩電解
金属化合物を高温で溶かして電気分解し金属だけを取り出す(アルミニウム、マグネシウムなど)。
- 電気めっき
下地にする金属を陰極にしてめっきする金属(金、銀、クロムなど)を析出させる。
化学の基礎
元素記号 (原子)と化学式
代表的な元素記号 (原子)
- O ― 酸素
- H ― 水素
- C ― 炭素
- S ― 硫黄
- K ― カリウム
- Na ― ナトリウム
- Cl ― 塩素
- Pb ― 鉛
- Cu ― 銅
- Ni ― ニッケル
代表的な化学式
- O2 ― 酸素
- H2 ― 水素
- H2O ― 水
- CO2 ― 二酸化炭素
- Cl2 ― 塩素
- NaCl ― 塩化ナトリウム
- NaOH ― ⽔酸化ナトリウム
- H2SO4 ― 希硫酸
化学式を使って、化学反応の様子を表したものを「化学反応式」といいます。
2NaCl + 2H2O → Cl 2 + 2NaOH + H2
2H2O → 2H2 + O2
原子量
すべての物質は、非常に小さい粒子が集まってできています。物質を構成する元になる粒子を「原子」といいます。原子は正の電荷を持つ原子核と、負の電荷を持つ電子から出来ています。さらに、原子核は正の電荷を持つ陽子と、電荷を持たない中性子から出来ています。原子核のもつ陽子の数を原子番号といい、陽子と中性子の数の合計を「質量数」といいます。
原子1個の質量は非常に小さいので、数値で扱うのは不便です。そのため、原子の質量は「相対質量」が使われます。原子量の基準は、質量数 12 の炭素原子(12C)です。炭素原子(12C)の質量を基準として、その数値を 12 としています。尚、単位はありません。
| 原子 | 原子1個の質量[g] | 相対質量 |
|---|---|---|
| 炭素(12C) | 19.927×10-24 | 12 |
| 水素(1H) | 1.6736×10-24 | 1 |
| 酸素(16O) | 26.561×10-24 | 16 |
分子量
分子の相対質量を分子量といいます。つまり、分子を構成している原子の原子量の総和のことです。例えば、水の分子量は、
| 水素の原子量(H2) | 酸素の原子量(O) | 水(H2O)の分子量 |
| 1×2個 | 16 | 2+16=18 |
アボガドロ定数
原子や分子,イオンは、一定の個数集団で扱います。この数を「アボガドロ定数」といいます。アボガドロ定数は 6.02×1023 個で、質量数が12の炭素原子中に含まれる原子の数です。
質量数が 12 の炭素原子(12C)が、6.02×1023 個集まると 12[g]になります。また、水(H2O)の分子量が、6.02×1023 個集まると 18[g]になります。
物質量
6.02×1023 個の粒子(原子や分子,イオン)の集団を 1[mol]と定め、mol単位で表した物質の量を、「物質量」といいます。1[mol]は、6.02×1023 個の粒子の集団で、その質量は、[g]量になります。
ファラデー定数
電子1モル(原子数=6.02×1023個)の電気量を「ファラデー定数」といいます。電子1個の電荷量は、1.603×10-19[C]ですので、
ファラデー定数
6.02×1023[個]×1.603×10-19[C/個]=96500[C]
また、1[A]の電流を流すには、1 秒間に 1[C]の電荷が移動します。ファラデー定数を、電流と時間の積算値で表すと、1時間は 3600[s]ですので、
96500/3600 ≒ 27[A・h/mol]
A・hは1時間あたりに流した電流量のことで、電気メッキや電池の容量など電気化学に関連した測定において多用される単位です。
原子価
ある原子が水素原子(H)と何個結合することが出来るかを示した数を「原子価」といいます。酸素原子(O)は水素原子(H)と 2 個結合して、水分子(H2O)になりますので、酸素の原子価は 2 です。
化学当量と電気化学当量
化学当量とは、化学反応における量的な比例関係を表す概念です。化学の領域において単に当量といえば化学当量を表します。化学当量は、「原子量/原子価」です。これにグラム[g]を付け加えたものを、「グラム当量」といいます。化学当量をファラデー定数(クーロン)で割ったものを、「電気化学当量」といいます。
ファラデーの法則
電気分解のとき、流れた電気量と生成または消費された物質の量との関係を示した法則をファラデーの法則といい、次の関係があります。
ファラデーの法則
第一法則:電極に析出される物質の量は、電解液中を通過した総「電気量」に比例する。
第二法則:電気量が同一の場合、析出される物質の量は、その物質の「電気化学当量」に比例する。
溶液などの液体に電気を流すと、金属が液体から分かれて電極に付着します。このように液体から個体が生成されることを「析出」といいます。
ファラデーの第一法則と第二法則には、次の公式があります。析出量を $w$[g]とすれば、次のようになります。
ファラデーの法則の公式
$w=\displaystyle\frac{1}{F}・\displaystyle\frac{m}{n}・I・t・η=\displaystyle\frac{1}{F}・\displaystyle\frac{m}{n}・Q$
$w$[g]:析出量
$F$:ファラデー定数($F=9.65×10^4$)
$m$[g/mol]:原子量
$n$:原子価
$I$[A]:電極間に流す電流量
$t$[hまたはs]:電流の流れた時間
$η$:電流効率
$Q$[A・h]:電気量
ファラデー定数は、$F=9.65×10^4$[C/mol]または $F=27$[Ah/mol]になります。$F=9.65×10^4$[C/mol]のときは、電流の流れた時間 $t$ は秒[s]で計算し、$F=27$[Ah/mol]のときは、電流の流れた時間 $t$ は時間[h]で計算します。
電験三種-機械の過去問解説:電気分解とファラデーの法則
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問8
ニッケル・カドミウム蓄電池の放電反応は、次の式で表される。
Cd+2NiOOH+2H2O→Cd(OH)2+2Ni(OH)2
いま、この電池のカドミウムが 11.2[g]放電したとき、得られる電気量[A・h]として、正しいのは次のうちどれか。ただし、カドミウムの原子量は 112、ファラデー定数は 26.8[A・h/mol]とする。
(1) 1.19 (2) 2.68 (3) 5.36 (4) 10.4 (5) 26.8
1997年(平成9年)問8 過去問解説
1モル 112[g]が放電すると 2[F]の電気量が得られますので、11.2[g]の放電で得られる電気量は、
2×26.8×11.2/112=5.36[A・h]
答え (3)
1998年(平成10年)問8
硝酸銀の溶液に直流電流 25[A]を1時間流したとき、析出する銀の量[g]の値として、正しいのは次のうちどれか。ただし、銀の原子量を 108、原子価を 1 とし、ファラデー定数は 27[A・h/mol]とする。
(1) 25 (2) 50 (3) 57 (4) 100 (5) 113
1998年(平成10年)問8 過去問解説
1モル108[g]析出するために 27[A・h]必要ですので、25[A・h]で析出できるのは、
108×25/27=100[g]
となります。
答え (4)
2000年(平成12年)問10
水の電気分解は次の反応により進行する。
2H2O → 2H2 + O2
このとき、アルカリ水溶液中では陽極(アノード)において、次の反応により酸素が発生する。
4OH– → O2 + 2H2O + 4e–
いま、2.7[kA・h]の電気量が流れたとき、論理的に得られる酸素の質量[kg]の値として、正しいのは次のうちどれか。ただし、酸素の原子量は 16、ファラデー定数は 27[A・h/mol]とする。
(1) 0.4 (2) 0.8 (3) 6.4 (4) 13 (5) 32
2000年(平成12年)問10 過去問解説
電子1モル(原子数=6.022×1023個)の電気量は、96500[C]で、この値をファラデー定数といいます。また、これをA・h単位では、96500[C]/ 3600[s]≒27[A・h/mol]となります。
4OH– → O2 + 2H2O + 4e–
の反応式から、2個の酸素原子に対して、4個の電子が関与し、この電子が電流となります。題意では、電子4個の電気量が 2.7[kA・h]なので、電子のモル数は、
2.7[kA・h]÷4個÷27[A・h/mol]=25[mol]
となります。25[mol]時の酸素の質量は、
25[mol]×16[g]×2[個]=800[g]=0.8[kg]
となります。ちなみに、気体1[mol]は、22.4[㍑]ですので、O2 の容量は、25×22.4=560[㍑]となります。
答え (2)
2001年(平成13年)問13
燃料電池は、水素と酸素の化学反応を利用したものである。燃料電池の電圧が 0.8[V]、電流効率が 90[%]であるとき、次の(a)及び(b)に答えよ。
ただし、水素の原子量は 1.0、ファラデー定数は 27[A・h/mol]とする。
(a) 反応によって 30[kg]の水素が消費されたとき、燃料電池から得られた電気量[kA・h]の値として、最も近いのは次のうちどれか。
(1) 360 (2) 410 (3) 580 (4) 730 (5) 900
(b) このとき得られた電気エネルギー[kW・h]の値として、最も近いのは次のうちどれか。
(1) 290 (2) 520 (3) 580 (4) 720 (5) 910
2001年(平成13年)問13 過去問解説
(a) 電子1モル(原子数=6.022×1023個)の電気量は、96500[C]で、この値をファラデー定数といいます。また、これをA・h単位では、96500[C]/ 3600[s]≒27[A・h/mol]となります。
水素の原子量は 1[g]、原子価は 1 で、グラム当量=(原子量)/(原子価)=1[g]です。 つまり、水素 1[g]で、27[A・h]の電気量が得られます。
水素 30[kg]で得られる電気量は、題意より、電流効率が 90[%]なので、
27×30×103×0.9×10-3≒730[kA・h]
答え (4)
(b) 燃料電池の電圧が 0.8[V]、電流効率 90[%]のときに得られた電気エネルギー P[kW・h]は、
P=730×0.8≒580[kW・h]
答え (3)
2004年(平成16年)問12
鉛蓄電池の放電反応は次の通りである。
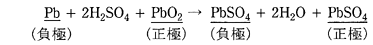
この電池を一定の電流で 2時間放電したところ、鉛の消費量は 42[g]であった。このとき流した電流[A]の値として、最も近いのは次のうちどれか。
ただし、鉛の原子量は 210、ファラデー定数は 27[A・h/mol]とする。
(1) 1.8 (2) 2.7 (3) 5.4 (4) 11 (5) 16
2004年(平成16年)問12 過去問解説
鉛蓄電池の負極,正極での反応を示します。
負極:Pb + SO42- → PbSO4 + 2e–
正極:PbO2 + SO42- + 4H+ + 2e- → PbSO4 + 2H2O
題意より、2時間の放電で 42/210[mol]の鉛が消費されたので、電流を $I$[A]とすると、鉛の原子価は 2 ですので、ファラデーの第二法則の公式より、
$w=\displaystyle\frac{1}{27}・\displaystyle\frac{m}{n}・I・T$
$42=\displaystyle\frac{1}{27}・\displaystyle\frac{210}{2}・I・2$
$I=\displaystyle\frac{42×27×2}{210×2}=5.4$[A]
答え (3)
2007年(平成19年)問13
硫酸亜鉛(ZnSO4)/硫酸系の電解液の中で陽極に亜鉛を、陰極に鋼帯の原板を用いた電気めっき法はトタンの製造法として広く知られている。今、両電極間に 2[A]の電流 5[h]通じたとき、原板に析出する亜鉛の量[g]の値として、最も近いのは次のうちどれか。
ただし、亜鉛の原子価(反応電子数)は 2 、原子量は 65.4 、電流効率は 65[%]、ファラデー定数 F=9.65×104 [C/mol]とする。
(1) 0.0022 (2) 0.13 (3) 0.31 (4) 7.9 (5) 16
2007年(平成19年)問13 過去問解説
ファラデーの第一法則の公式より、
$w=\displaystyle\frac{1}{96500}・\displaystyle\frac{m}{n}・I・t$
$=\displaystyle\frac{1}{96500}・\displaystyle\frac{65.4}{2}・2・5×3600×0.65$
$≒7.9$[g]
答え (4)
電験三種の機械科目に出題される「照明」のページ
電験三種の機械科目に出題される「電熱」のページ
電験三種の機械科目に出題される「電気化学(電池)」のページ
- 電気分解とファラデーの法則
- 電気化学(電池)と電気加工






