計測と測定誤差

このページでは、計測と測定誤差について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された計測と測定誤差の過去問題の解き方も解説しています。

計測の種類
測定誤差
電験三種－理論（電気・電子計測）過去問題

計測の種類

ある量を測定するとき、前の状態からの変化を見る「偏位法」と、ある基準値と等しいかを見る「零位法」があります。

偏位法の例としては電圧計・電流計などがあります。指示値は0にセットされた量からの偏位です。零位法の例としては電位差計やブリッジ回路などがあり、一方の量を基準の電位に合わせることにより零位に持っていきます。

測定誤差

測定値 $M$ から真の値 $T$ を引いた値を誤差 $ϵ$ といいます。誤差は次の式で求めることができます。

$ϵ=M-T$

誤差 $ϵ$ と真の値 $T$ との比を相対誤差または誤差率[%]といい、測定の精度を表します。

$％ϵ=\displaystyle\frac{ϵ}{T}×100=\displaystyle\frac{M−T}{T}×100$[%]

真の値は、測定される量の正しい値ですが、実際には求めることができませんので、真の値とみなせる値をいいます。また誤差には、読取り誤差、測定方法や測定器の不備、環境による誤差などがあります。

電験三種－理論（電気・電子計測）過去問題

1997年（平成9年）問10

図のような回路において、電圧計を用いて端子ab間の電圧を測定したい。そのとき、電圧計の内部抵抗 $R$ が無限大でないことによって生じる測定誤差を 2 [%]以内とするためには、内部抵抗 $R$ [kΩ] の最小値をいくらにすればよいか。正しい値を次のうちから選べ。

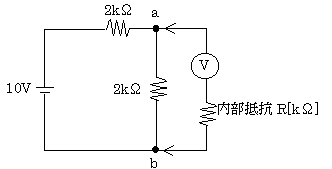
(1) 38　(2) 49　(3) 52　(4) 65　(5) 70

1997年（平成9年）問10　過去問解説

電圧計の内部抵抗Rが無限大で理想的な場合は、真値となります。真値を $V_T$ [V]とすると、

$V_T=\displaystyle\frac{10}{2+2}×2=5$ [V]

電圧計の内部抵抗が $R$ [kΩ] のときの測定値を $V_M$ [V] とすると、

$V_M=\displaystyle\frac{10}{2+\displaystyle\frac{2R}{2+R}}×\displaystyle\frac{2R}{2+R}=\displaystyle\frac{5R}{1+R}$ [V]

測定値を $V_M$ [V]は、真値を $V_T$ [V]より小さくなりますので、誤差 $ϵ$ はマイナスの値になります。つまり誤差率 $％ϵ$ は $-2$ [％] となります。

$％ϵ≦\displaystyle\frac{M−T}{T}×100$ [%]

$-2≦\displaystyle\frac{\displaystyle\frac{5R}{1+R}−5}{5}×100$

この式を解くと $R≧49$ [kΩ] となります。

答え (2)

1999年（平成11年）問10

電圧計(Ｖ)及び電流計(Ａ)を用いて負荷抵抗 $R$ [Ω] で消費される直流電力を測定するとき、計器の接続を図１又は図２とした場合のそれぞれの測定値の誤差 $ε_1$ 及び $ε_2$ を表す式として、正しいものを組み合わせたのは次のうちどれか。
ただし、電圧計の内部抵抗を $r_v$ [Ω]、電流計の内部抵抗を $r_i$ [Ω]、負荷電圧を $V_o$ [V]、負荷電流を$I_o$ [A] とする。

1999年（平成11年）問10　過去問解説

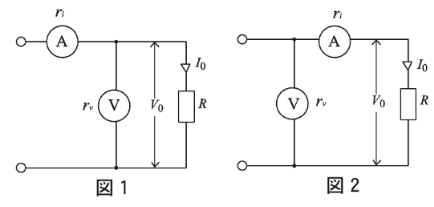
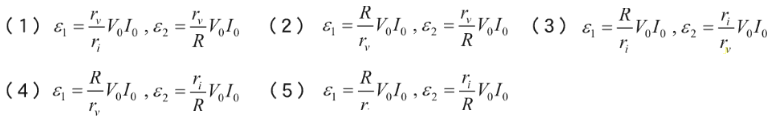
電圧計(Ｖ)の指示値を $V$ [V]、電流計(Ａ)の指示値を $I$ [A] とすると、図１では

$V=V_o$

$I=I_o+\displaystyle\frac{V_o}{r_v}$

図１の電力の測定値を $P_1$ [W] とすると、

$P_1=VI=V_o\left(I_o+\displaystyle\frac{V_o}{r_v}\right)$

電力の真値を $P_o$ [W] とすると、$P_o=V_oI_o$ [W] ですので、測定値の誤差 $ε_1$ は、

$ε_1=V_o\left(I_o+\displaystyle\frac{V_o}{r_v}\right)-V_oI_o=\displaystyle\frac{V_o^2}{r_v}$

$V_o=I_oR$ より

$ε_1=\displaystyle\frac{V_o^2}{r_v}=\displaystyle\frac{R}{r_v}V_oI_o$

図２では

$V=V_o+I_or_i$

$I=I_o$

図２の電力の測定値を $P_2$ [W] とすると、

$P_2=VI=(V_o+I_or_i)I_o$

測定値の誤差 $ε_2$ は、

$ε_2=(V_o+I_or_i)I_o-V_oI_o=I_o^2r_i$

$I_o=\displaystyle\frac{V_o}{R}$ より

$ε_2=I_o^2r_i=\displaystyle\frac{r_i}{R}V_oI_o$

答え (4)

2008年（平成20年）問14

最大目盛 100 [ｍA] 、階級1.0級（JIS)の単一レンジの電流計がある。この電流計で 40 [ｍA] を測定するときに、この電流計に許されている誤差 [ｍA] の大きさの最大値として、正しいのは次のうちどれか。

(1) 0.2　(2) 0.4　(3) 1.0　(4) 2.0　(5) 4.0

2008年（平成20年）問14　過去問解説

指示計器は、測定値上限に対する許容誤差の値の割合を階級として表します。例えば、最大目盛 100 [A] の電流計の許容誤差が 1.0[A] であれば、精度階級は 1.0 級となります。

最大目盛 100 [ｍA] で階級が 1.0 級の誤差 [ｍA] の大きさの最大値は、1.0 [ｍA] になります。

答え (3)

2010年（平成22年）問16

電力量計について、次の(a)及び(b)の問に答えよ。

(a) 次の文章は、交流の電力量計の原理について述べたものである。
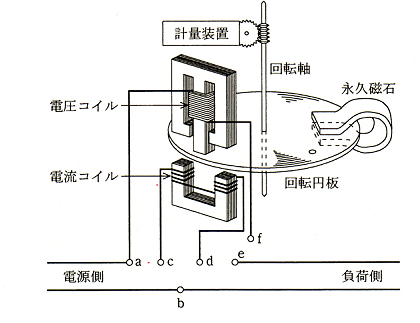
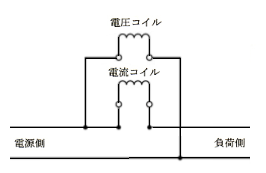
計器の指針等を駆動するトルクを発生する動作原理により計器を分類すると、図に示した構造の電力量計の場合は、（　ア　）に分類される。
この計器の回転円板が負荷の電力に比例するトルクで回転するように、図中の端子 a から f を（　イ　）のように接続して、負荷電圧を電圧コイルに加え、負荷電流を電流コイルに流す。その結果、コイルに生じる磁束による移動磁界と、回転円板上に生じる渦電流との電磁力の作用で回転円板は回転する。
一方、永久磁石により回転円板には速度に比例する（　ウ　）が生じ、負荷の電力に比例する速度で回転円板は回転を続ける。したがって、計量装置でその回転数をある時間計量すると、その値は同時間中に消費された電力量を示す。

上記の記述中の空白個所(ア)，(イ)及び(ウ)に当てはまる語句又は記号として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）
（１）	誘導形	ａｃ，ｄｅ，ｂｆ	駆動トルク
（２）	電流力計形	ａｄ，ｂｃ，ｅｆ	制動トルク
（３）	誘導形	ａｃ，ｄｅ，ｂｆ	制動トルク
（４）	電流力計形	ａｄ，ｂｃ，ｅｆ	駆動トルク
（５）	電力計形	ａｃ，ｄｅ，ｂｆ	駆動トルク

(b) 上記(a)の原理の電力量計の使用の可否を検討するために、電力量計の計量の誤差率を求める実験を行った。実験では、3 [kW] の電力を消費している抵抗負荷の交流回路に、この電力量計を接続した。このとき、電力量計はこの抵抗負荷の消費電力量を計量しているので、計器の回転円板の回転数を測定することから計量の誤差率を計算できる。
電力量計の回転円板の回転数を測定したところ、回転数は1分間に61であった。この場合、電力量計の計量の誤差率 [％] の大きさとして、最も近いのは次のうちのどれか。
ただし、電力量計の計器定数（ 1 [kW・h] 当たりの回転円板の回転数）は、1200 [rev/kW・h] であり、回転円板の回転数と計量装置の計量値の関係は正しいものとし、電力損失は無視できるものとする。

(1) 0.2　(2) 0.4　(3) 1.0　(4) 1.7　(5) 2.1

2010年（平成22年）問16　過去問解説

(a) 負荷電圧を電圧コイルに加えるためには、負荷と並列に電圧コイルを接続します。電圧コイルは a-f 間に電圧を印加する必要がありますので、端子bとfを接続します。
負荷電流を電流コイルに流すためには、回路に直列に電流コイルを接続します。電流コイルには、a→c→d→eの経路で電流を流す必要がありますので、図中の端子aとc，dとeを接続します。
その結果、コイルに生じる磁束による移動磁界と回転円板上に生じる渦電流との電磁力の作用で駆動トルクが発生し、回転円板は回転します。

答え (3)

(b) 電力量計の計器定数を $K$ とすると、１分間の回転数 $T$ は、

$T=\displaystyle\frac{K×3×60}{60×60}=\displaystyle\frac{1200×3×60}{60×60}=60$

百分率誤差（誤差率） [%] は、 $％ϵ=\displaystyle\frac{ϵ}{真の値}×100$ [%] ですので、

$％ϵ=\displaystyle\frac{ϵ}{真の値}×100=\displaystyle\frac{61-60}{60}×100≒1.7$ [%]

答え (4)

2016年（平成28年）問16

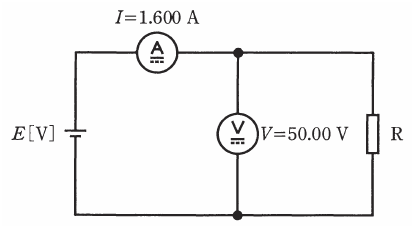
図のような回路において、抵抗 $R$ の値 [Ω] を電圧降下法によって測定した。この測定で得られた値は、電流計 $I=1.600A$、電圧計 $V=50.00V$ であった。次の(a)及び(b)の問に答えよ。
ただし、抵抗 $R$ の真の値は $31.21Ω$ とし、直流電源、電圧計及び電流計の内部抵抗の影響は無視できるものである。また、抵抗 $R$ の測定値は有効数字4桁で計算せよ。