第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「抵抗の測定(電圧降下法・ダブルブリッジ法)」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「抵抗の測定(電圧降下法・ダブルブリッジ法)」などの過去問題も解説しています。
抵抗の測定
電圧降下法
電圧降下法は、抵抗に電流を流してそのときの抵抗の電圧降下と電流を測定し、オームの法則で抵抗値を求める方法です。電圧計と電流計には内部抵抗が含まれているので、正確な電圧計と電流計の内部抵抗を知っておく必要があります。測定値は、電圧計と電流計の内部抵抗を考慮して補正します。
電圧降下法の接続方法には2通りあり、接続方法を使い分けることで誤差が小さくなります。
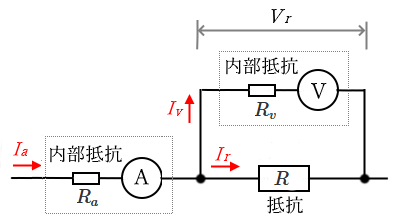
① 電圧計の内部抵抗 $R_v$ が測定したい抵抗 $R$ より十分に大きい場合($R_v≫R$)
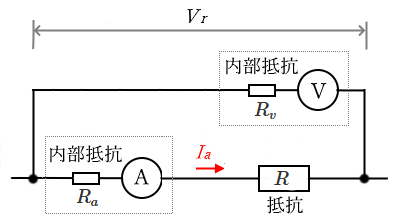
② 電流計の内部抵抗 $R_a$ が測定したい抵抗 $R$ より十分に小さい場合($R_a≪R$)
電圧降下法①:
電圧計の内部抵抗 $R_v$ が測定したい抵抗 $R$ より十分に大きい場合($R_v≫R$)の接続方法
$R=\displaystyle\frac{V_r}{I_a-\displaystyle\frac{V_r}{R_v}}$
$R$[Ω]:抵抗
$R_v$[Ω]:電圧計の内部抵抗
$I_a$[A]:測定電流
$V_r$[V]:測定電圧
電圧降下法②:
電流計の内部抵抗 $R_a$ が測定したい抵抗 $R$ より十分に小さい場合($R_a≪R$)の接続方法
$R=\displaystyle\frac{V_r}{I_a}-R_a$
$R$[Ω]:抵抗
$R_a$[Ω]:電流計の内部抵抗
$I_a$[A]:測定電流
$V_r$[V]:測定電圧
ブリッジ法
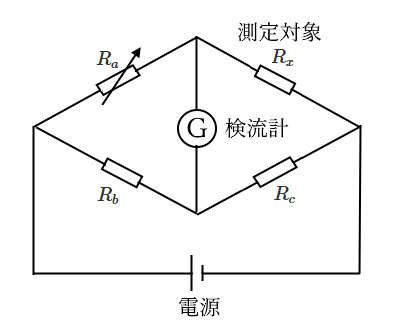
ブリッジ回路から、未知の抵抗 $R_x$ を求める方法です。ホイートストンブリッジの平衡条件 $R_xR_b=R_aR_c$ より、可変抵抗 $R_a$ の値を変化させて、 $R_x$ の値を求めます。
ブリッジ法:
可変抵抗 $R_a$ を調整して、検流計 G がゼロを指したときにブリッジが平衡
ブリッジの平衡条件
$R_x=\displaystyle\frac{R_c}{R_b}R_a$
$R_x$[Ω]:測定抵抗
$R_a$[Ω]:可変抵抗
$R_b$[Ω]:抵抗
$R_c$[Ω]:抵抗
ケルビンダブルブリッジ法
ケルビンダブルブリッジ法は、ブリッジ回路を2重化したもので、数mΩの抵抗を測定する際に利用されます。
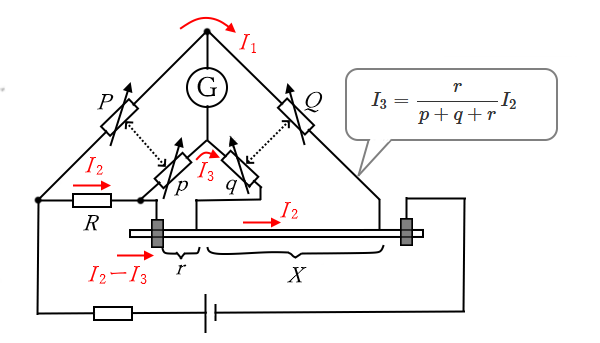
図の回路のブリッジの平衡条件は、
$PI_1=RI_2+pI_3$ … (1)
$QI_1=XI_2+qI_3$ … (2)
$I_2$ と $I_3$ の関係は、
$I_3(p+q)=(I_2-I_3)r$
$I_3=\displaystyle\frac{r}{p+q+r}I_2$ … (3)
(1),(2),(3)式より
$PI_1=\left(R+\displaystyle\frac{pr}{p+q+r}\right)I_2$
$QI_1=\left(X+\displaystyle\frac{qr}{p+q+r}\right)I_2$
したがって、
$\displaystyle\frac{P}{Q}=\displaystyle\frac{R+\displaystyle\frac{pr}{p+q+r}}{X+\displaystyle\frac{qr}{p+q+r}}$
$X=\displaystyle\frac{QR}{P}+\displaystyle\frac{pr}{p+q+r}\left(\displaystyle\frac{Q}{P}-\displaystyle\frac{q}{p}\right)$
ここで、
$\displaystyle\frac{Q}{P}=\displaystyle\frac{q}{p}$
の条件が常に満たされていると、
$X=\displaystyle\frac{QR}{P}$
が成り立ち、ホイートストンブリッジと同じ関係式になります。
接地抵抗の測定
接地抵抗計を使用した接地抵抗の測定原理を図に示します。
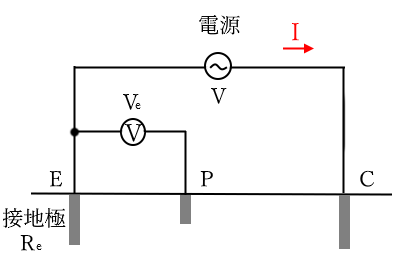
接地極 $E$と補助極 $C$ の間に交流電圧 $V$ をかけて電流 $I$ を流し、接地極 $E$ と補助極 $P$ の間の電圧 $V_e$ を測定します。これより、極地極 $E$ の接地抵抗 $R_e$ が次式により求めることができます。
$Re=\displaystyle\frac{Ve}{I}$
電験三種-理論の過去問解説:抵抗の測定
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2001年(平成13年)問9【電験理論の過去問題】
図のような抵抗測定回路を内蔵する回路計(テスタ)を用いて、抵抗 Rx の値を測定したい。この回路計の零オーム調整を行った後に、抵抗 Rx の値を測定したところ、電流計の指針は最大目盛の 1/5 を示した。測定した抵抗 Rx [kΩ] の値として、正しいのはどれか。
ただし、電池の電圧 E=3 [V]、電流計の最大目盛は 500 [μA] とし、Rs は零オーム調整用抵抗を含めた回路の等価抵抗である。
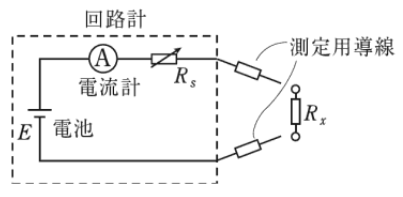
(1) 21 (2) 24 (3) 27 (4) 30 (5) 33
回路計(テスタ)の零オーム調整とは、測定用導線(プローブ)を短絡させて、指針がゼロになるように調整することです。したがってこのときは、回路の抵抗は $R_S$ だけになりますので、
$R_S=\displaystyle\frac{3}{500×10^{-6}}=6×10^3$ [Ω]
抵抗 Rx の値を測定したときに、回路に流れる電流を $I$ [A]とすると
$I=\displaystyle\frac{E}{R_S+R_X}=\displaystyle\frac{3}{6×10^3+R_X}$
一方で、抵抗 Rx の値を測定したところ、電流計の指針は最大目盛の 1/5 になりますので、
$I=500×10_{-6}×\displaystyle\frac{1}{5}=100×10^{-6}$ [A]
したがって、
$\displaystyle\frac{3}{6×10^3+R_X}=100×10^{-6}$
$R_X=24$ [kΩ]
答え (2)
2002年(平成14年)問11【電験理論の過去問題】
図のように、それぞれ十分離れた3点A、B、Cの地中に接地極が埋設されている。次の(a)及び(b)に答よ。
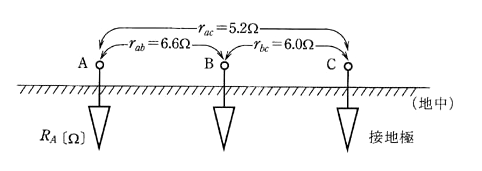
(a) AB間、BC間、AC間の抵抗を測定したところ、それぞれ $r_{ab}=6.6$ [Ω]、 $r_{bc}=6.0$ [Ω]、 $r_{ac}=5.2$ [Ω]であった。このときのA点の接地抵抗 $R_A$ [Ω] の値として、正しいのはどれか。
(1) 2.2 (2) 2.9 (3) 3.6 (4) 5.8 (5) 7.2
(b) B点とC点を導線で短絡したときのAB間の抵抗 $r’_{ab}$ [Ω] の値として、最も近いのはどれか。
ただし、導線の抵抗は無視できるものとする。
(1) 1.9 (2) 3.8 (3) 4.3 (4) 5.2 (5) 6.6
(a) B点の接地抵抗 $R_B$ [Ω]、C点の接地抵抗 $R_C$ [Ω]とすると、題意より
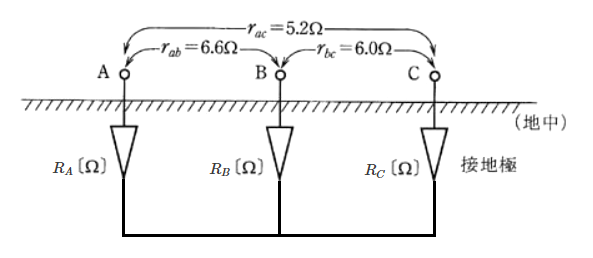
$R_A+R_B=r_{ab}=6.6$[Ω] … (1)
$R_A+R_C=r_{ac}=5.2$[Ω] … (2)
$R_B+R_C=r_{bc}=6.0$[Ω] … (3)
(1),(2),(3)式を解くと
$R_A=2.9$[Ω] ,$R_B=3.7$[Ω],$R_C=2.3$[Ω]
答え (2)
(b) 問題を等価回路で示します。
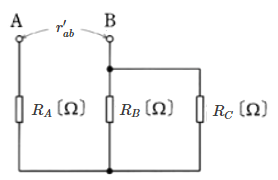
図より合成抵抗は、
$r’_{ab}=R_A+\displaystyle\frac{R_BR_C}{R_B+R_C}=2.9+\displaystyle\frac{3.7×2.3}{3.7+2.3}≒4.3$[Ω]
答え (3)
2004年(平成16年)問17【電験理論の過去問題】
図は抵抗 Rab [kΩ]のすべり抵抗器、抵抗 Rd [kΩ]、抵抗 Re [kΩ]と直流電圧 Es=12 [V]の電源を用いて、端子H、G 間に接続した未知の直流電圧[V]を測るための回路である。次の(a)及び(b)に答よ。
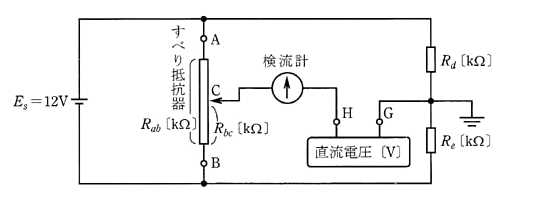
(a) 抵抗 Rd=5 [kΩ]、抵抗 Re=5 [kΩ] として、直流電圧 3 [V] の電源の正極を端子Hに、負極を端子Gに接続した。すべり抵抗器の接触子Cの位置を調整して検流計の電流を零にしたところ、すべり抵抗器の端子Bと接触子C間の抵抗 Rbc=18 [kΩ] となった。すべり抵抗器の抵抗 Rab [kΩ] の値として、正しいものは次のうちどれか。
(1) 18 (2) 24 (3) 36 (4) 42 (5) 50
(b) 次に、直流電圧 3 [V] の電源を取り外し、未知の直流電圧 Ex [V] の電源を端子 H、G 間に接続した。抵抗 Rd=2 [kΩ]、抵抗 Re=22 [kΩ] としてすべり抵抗器の接触子Cの位置を調整し、すべり抵抗器の端子Bと接触子C 間の抵抗 Rbc=12 [kΩ]としたときに、検流計の電流が零となった。このときの Ex [V] の値として、正しいものは次のうちどれか。
ただし、端子Gを電位の基準(0[V])とする。
(1) -5 (2) -3 (3) 0 (4) 3 (5) 5
(a) 次の図に示すように、直流電圧を開放した場合のCD間の電位差 $V_{cd}$ は、
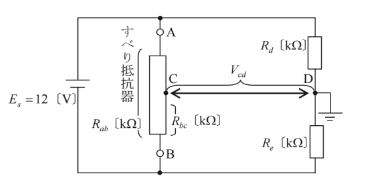
$V_{cd}=\displaystyle\frac{E_s}{R_{ab}}×R_{bc}-\displaystyle\frac{E_s}{R_d+R_e}×R_e$
直流電源を接続すると、検流計は零になりますので、電位差 $V_{cd}$ は3 [V] になります。
$3=\displaystyle\frac{12}{R_{ab}}×18-\displaystyle\frac{12}{5+5}×5$
$R_{ab}=24$ [kΩ]
答え (2)
(b) 直流電圧 $E_x$ [V]は、
$\begin{eqnarray}E_x&=&\displaystyle\frac{E_s}{R_{ab}}×R_{bc}-\displaystyle\frac{E_s}{R_d+R_e}×R_e\\\\&=&\displaystyle\frac{12}{24}×12-\displaystyle\frac{12}{2+22}×22\\\\&=&-5 [V]\end{eqnarray}$
答え (1)
2006年(平成18年)問16【電験理論の過去問題】
図のブリッジ回路を用いて、未知抵抗 RX を測定したい。抵抗 R1=3 [kΩ]、R2=2 [kΩ]、R4=3 [kΩ] とし、R3=6 [kΩ] の滑り抵抗器り接触子の接点Cをちょうど中央に調整したとき( Rac=Rbc=3 [kΩ])ブリッジが平衡したという。次の(a)及び(b)に答えよ。
ただし、直流電圧電源は 6 [V] とし、電流計の内部抵抗は無視できるものとする。
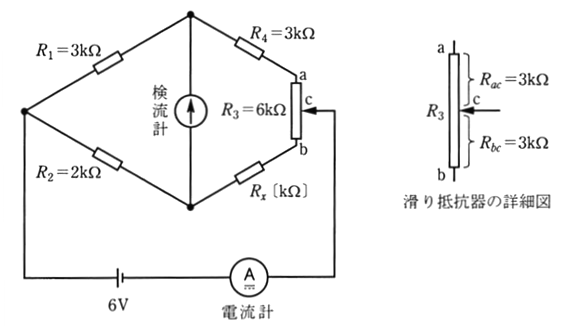
(a) 未知抵抗 RX [kΩ] の値として、正しいのは次のうちどれか。
(1) 0.1 (2) 0.5 (3) 1.0 (4) 1.5 (5) 2.0
(b) 平衡時の電流計の指示値 [mA] として、最も近いのは次のうちどれか。
(1) 0 (2) 0.4 (3) 1.5 (4) 1.7 (5) 2.0
(a) ブリッジ回路の平衡条件より
$3(R_x+3)=2(3+3)$
$R_x=1$[kΩ]
答え (3)
(b) 電源側からみた回路の合成抵抗を $R$ [Ω] とすると、
$R=\displaystyle\frac{(2+4)×10^3×(3+6)×10^3}{(2+4)×10^3+(3+6)×10^3}=\displaystyle\frac{18}{5}×10^3$ [Ω]
電流計の指示値 $I$ [mA] は、
$I=\displaystyle\frac{6}{\displaystyle\frac{18}{5}×10^3}=1.7$ [mA]
答え (4)
2009年(平成21年)問15【電験理論の過去問題】
電気計測に関する記述について、次の(a)及び(b)に答えよ。
(a) ある量の測定に用いる方法には各種あるが、指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法を( ア )法という。これに比較して精密な測定を行う場合に用いられている( イ )法は、測定量と同種類で大きさを調整できる既知量を別に用意し、既知量を測定量に平衡させて、そのときの既知量の大きさから測定量を知る方法である。( イ )法を用いた測定器の例としては、ブリッジや( ウ )がある。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 偏位 | 零位 | 直流電位差法 |
| (2) | 偏位 | 差動 | 誘導形電力量計 |
| (3) | 間接 | 零位 | 直流電位差法 |
| (4) | 間接 | 差動 | 誘導形電力量計 |
| (5) | 偏位 | 零位 | 誘導形電力量計 |
(b) 図は、ケルビンダブルブリッジの原理図である。図において $R_x$ [Ω] が未知の抵抗、 $R_s$ [Ω] は可変抵抗、 $P$ [Ω]、$Q$ [Ω]、$p$ [Ω]、$q$ [Ω] は固定抵抗である。このブリッジは、抵抗 $R_x$ [Ω] のリード線の抵抗が、固定抵抗 $r$ [Ω] 及び直流電源側の接続線に含まれる回路構成となっており、低い抵抗の測定に適している。
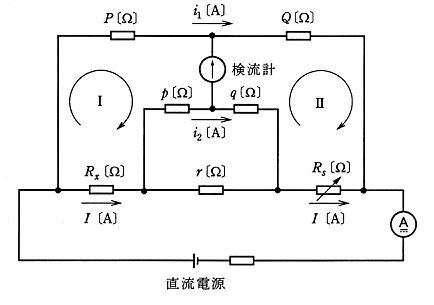
図の回路において、固定抵抗 $P$ [Ω]、 $Q$ [Ω]、 $p$ [Ω]、 $q$ [Ω] の抵抗値が( ア )= 0 の条件を満たしていて、可変抵抗 $R_s$ [Ω]、固定抵抗 $r$ [Ω] においてブリッジが平衡している。この場合は、次式から抵抗 $R_x$ [Ω] が求まる。
$R_x=(( イ ))R_s$
この式が求まることを次の手順で証明してみよう。

上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる式として、正しいものを組み合わせたには次のうちどれか。

(a) ある量の測定に用いる方法には各種あるが、指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法を( 偏位 )法という。これに比較して精密な測定を行う場合に用いられている( 零位 )法は、測定量と同種類で大きさを調整できる既知量を別に用意し、既知量を測定量に平衡させて、そのときの既知量の大きさから測定量を知る方法である。( 零位 )法を用いた測定器の例としては、ブリッジや( 直流電位差計 )がある。
答え (1)
(b) (ウ)に入るのは、$(p+q)i_2=r(I-i_2)$ より、
$(p+q+r)i_2=rI$
$\displaystyle\frac{i_2}{I}=\displaystyle\frac{r}{p+q+r}$ … ④
$\displaystyle\frac{i_2}{I}=K$ として整理していくと、
$\displaystyle\frac{P}{Q}=\displaystyle\frac{R_x+pK}{R_s+qK}$
$Q(R_x+pK)=P(R_s+qK)$
$R_x=\displaystyle\frac{P}{Q}R_s+(\displaystyle\frac{P}{Q}-\displaystyle\frac{p}{q})qK$ … ⑤
答え (1)
電験三種の理論科目に出題される「電気・電子計測分野」のページ
1.指示計器の種類と特徴
2.計測と測定誤差
3.電圧と電流の測定(倍率器と分流器)
4.抵抗の測定(電圧降下法・ダブルブリッジ法)
5.電力計の原理と二電力計法
6.オシロスコープの周波数測定






