電験三種の法規で出題される力率の計算について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の試験で、実際に出題された過去問題も解説しています。
交流電力の力率補正
交流回路で実際に消費される電気エネルギーを有効電力といい、負荷と電源間で一時的に電磁エネルギーや静電エネルギーの形で蓄えられ、エネルギーが往復するだけで消費されない電力を無効電力といいます。また、有効電力と無効電力のベクトル和を、皮相電力といいます。
皮相電力に対する有効電力の割合を力率といいます。力率は cosθ で表し、θ を力率角といいます。
負荷にかかる電圧を V[V]、流れる電流を I[A]、力率を cosθ とすると、有効電力 P[W]、無効電力 Q[var]、皮相電力 S[V⋅A]は次の式で表わすことができます。
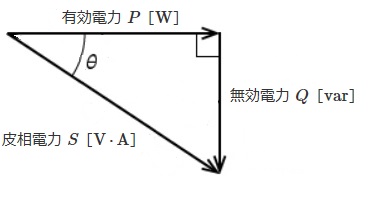
有効電力 $P=VIcosθ[W]$
無効電力 $Q=VIsinθ[var]$
皮相電力 $S=VI[V⋅A]$
力率改善
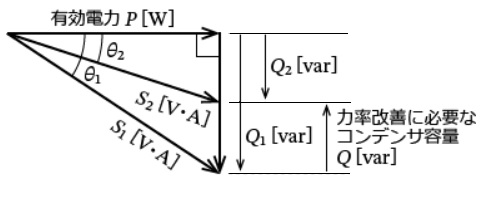
力率改善の計算は、有効電力 P[W]、無効電力 Q[var]、皮相電力 S[V⋅A]のベクトル図で示し、三平方の定理や三角関数を用いて計算します。
よく使う三角関数の公式です。
$sinθ=\sqrt{ 1-cos^2 θ}$
$tanθ=\displaystyle \frac{ sinθ }{ cosθ }=\displaystyle \frac{ \sqrt{ 1-cos^2 θ} }{ cosθ }$
電験三種-法規(施設管理)過去問題
1997年(平成9年)問12
定格容量 1000[kVA]の変圧器から 680[kW]、遅れ力率0.8の負荷に電力を供給している。いま、120[kW]、遅れ力率 0.6 の負荷を増設する必要を生じた。変圧器を増設しないで、力率改善により対処する場合、設置すべきコンデンサの最小の容量[kvar]はいくらか。正しい値を次のうちから選べ。
(1) 50 (2) 70 (3) 160 (4) 200 (5) 510
1997年(平成9年)問12 過去問解説
設問を図に示します。
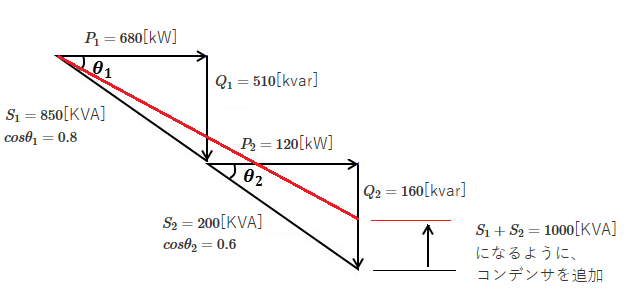
接続されている負荷の皮相電力を $S_1$[kVA]、無効電力を $Q_1$[kvar]とすると、
$S_1=\displaystyle \frac{ P_1}{cosθ_1 }=\displaystyle \frac{ 680 }{0.8 }=850[kVA]$
$Q_1=S_1sinθ=850×0.6=510[kvar]$
接続する負荷の皮相電力を $S_2$[kVA]、無効電力を $Q_2$[kvar]とすると、
$S_2=\displaystyle \frac{ P_2}{cosθ_2 }=\displaystyle \frac{ 120 }{0.6 }=200[kVA]$
$Q_2=S_2sinθ=200×0.8=160[kvar]$
設置すべきコンデンサの容量を $Q_3$[kvar]とすると、
$1000=\sqrt{(680+120)^2+(510+160-Q_3)^2}$
$=\sqrt{(800)^2+(670-Q_3)^2}$
これを計算すると、$Q_3=70[kvar]$
答え (2)
1999年(平成11年)問12
使用電力 600[kW]、遅れ力率 80[%]の三相負荷に電力を供給している配電線路がある。負荷と並列に電力用コンデンサを接続して線路損失を最小とするために必要なコンデンサの容量[kvar]はいくらか。正しい値を次のうちから選べ。
(1) 350 (2) 400 (3) 450 (4) 500 (5) 550
1999年(平成11年)問12 過去問解説
線路損失を最小にするには、負荷の無効電力をすべて打ち消す容量のコンデンサを接続します。接続されている負荷の皮相電力を $S$[kVA]、有効電力を $P$[kW]、無効電力を $Q$ [kvar] とすると、
$S=\displaystyle \frac{ P}{cosθ }=\displaystyle \frac{ 600 }{0.8 }=750[kVA]$
$Q=Ssinθ=750×0.6=450[kvar]$
答え (3)
2001年(平成13年)問11
10,000[kVA]、遅れ力率 80[%]の負荷に電力を供給している変電所がある。負荷と並列に 2,000[kvar]のコンデンサを設置した場合、次の(a)及び(b)に答えよ。
(a) コンデンサ設置後の無効電力[kvar]の値として、正しいのは次のうちどれか。
(1) 1000 (2) 2000 (3) 3000 (4) 4000 (5) 5000
(b) 変圧器にかかる負荷の力率[%]の値として、正しいのは次のうちどれか。
(1) 86.8 (2) 89.4 (3) 93.0 (4) 95.2 (5) 97.5
2001年(平成13年)問11 過去問解説
(a) 接続されている負荷の皮相電力を $S$[kVA]、有効電力を $P$[kW]、無効電力を $Q$[kvar]とすると、
$P=Scosθ=10000×0.8=8000[kW]$
$Q=Ssinθ=10000×0.6=6000[kvar]$
コンデンサ設置後の無効電力[kvar]は、
$6000-2000=4000$[kvar]
答え (4)
(b) コンデンサを設置した後の皮相電力を $S_2$[kVA]、無効電力を $Q_2$[kvar]とすると、
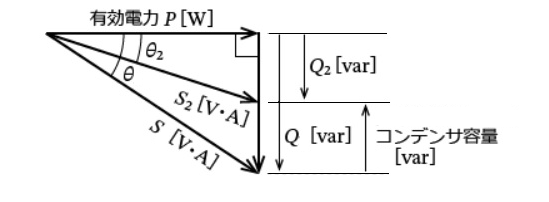
$\begin{eqnarray}S_2&=&\sqrt{P^2+Q_2^2}\\\\&=&\sqrt{8000^2+4000^2}\\\\&=&1000\sqrt{80}[kVA]\end{eqnarray}$
変圧器にかかる負荷の力率[%]は、
$\begin{eqnarray}力率&=&\displaystyle \frac{ P}{S_2 }×100\\\\&=&\displaystyle \frac{ 8000}{1000\sqrt{80} }×100\\\\&=&89.4[%]\end{eqnarray}$
答え (2)
2002年(平成14年)問9
使用電力 50[kW]、遅れ力率 0.8 の平衡三相負荷がある。この負荷と並列に電力用コンデンサを接続して、力率を 1.0 にするために必要なコンデンサの容量[kvar]の値として、正しいのは次のうちどれか。
(1) 24.5 (2) 30.0 (3) 37.5 (4) 40.0 (5) 62.5
2002年(平成14年)問9 過去問解説
接続されている負荷の皮相電力を $S$[kVA]、有効電力を $P$[kW]、無効電力を $Q$[kvar]とすると、
$S=\displaystyle \frac{ P}{cosθ }=\displaystyle \frac{ 50 }{0.8 }=62.5[kVA]$
$Q=Ssinθ=62.5×0.6=37.5[kvar]$
この無効分をコンデンサで打ち消すと、力率は1になります。
答え (3)
2006年(平成18年)問12
定格容量 500[kVA]の三相変圧器に 400[kW](遅れ力率 0.8 )平衡三相負荷が接続されている。これに新たに 60[kW](遅れ力率 0.6 )の平衡三相負荷を追加接続する場合について、次の(a)及び(b)の答えよ。
(a) コンデンサを設置していない状態で、新たに負荷を追加した場合の合成負荷の力率として、最も近いのは次のうちどれか。
(1) 0.65 (2) 0.71 (3) 0.73 (4) 0.75 (5) 0.77
(b) 新たに負荷を追加した場合、変圧器が過負荷運転とならないために設置するコンデンサ設備の必要最小の定格設備容量[kvar]の値として、最も適切なのは次のうちどれか。
(1) 50 (2) 100 (3) 150 (4) 200 (5) 300
2006年(平成18年)問12 過去問解説
(a) 接続されている負荷の皮相電力を $S_1$[kVA]、有効電力を $P_1$[kW]、無効電力を $Q_1$[kvar]とすると、
$S_1=\displaystyle \frac{ P_1}{cosθ_1 }=\displaystyle \frac{ 400 }{0.8 }=500[kVA]$
$Q_1=S_1sinθ=320×0.6=300[kvar]$
接続する負荷の皮相電力を $S_2$[kVA]、有効電力を $P_2$[kW]、無効電力を $Q_2$[kvar]とすると、
$S_2=\displaystyle \frac{ P_2}{cosθ_2 }=\displaystyle \frac{ 60 }{0.6 }=100[kVA]$
$Q_2=S_2sinθ=100×0.8=80[kvar]$
合成有効電力は $400+60=460$[kW]、合成無効電力は $300+80=380$[kvar]になります。合成負荷の力率は、
$合成負荷の力率=\displaystyle \frac{ 460}{\sqrt{460^2+380^2} }=0.77$
答え (5)
(b) 設問を図に示します。
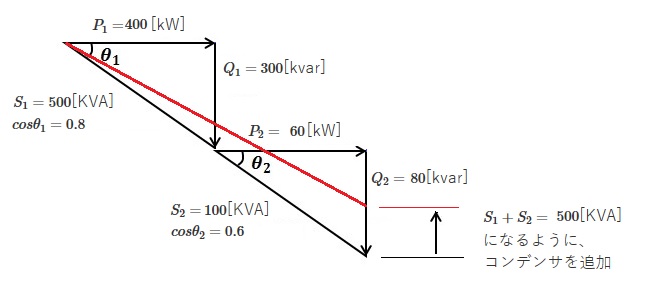
設置すべきコンデンサの容量を $Q_3$[kvar]とすると、
$500=\sqrt{(460)^2+(380-Q_3)^2}$
これを計算すると、$Q_3=184$[kvar]となります。この容量より大きなコンデンサを必要とします。直近上位の、200が正解になります。
答え (4)
2012年(平成24年)問12
電気事業者から供給を受ける、ある需要家の自家用変電所を送電端とし、高圧三相3線式1回線の専用配電線路で受電している第2工場がある。 第2工場の負荷は 2000[kW]、受電電圧は 6000[V]であるとき、第2工場の力率改善及び受電端電圧の調整を図るため、第2工場に電力用コンデンサを設置する場合、次の(a)及び(b)の問に答えよ。
ただし、第2工場の負荷の消費電力及び負荷力率(遅れ)は、受電端電圧によらないものとする。
(a) 第2工場の力率改善のために電力用コンデンサを設置したときの受電端のベクトル図として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、ベクトル図の文字記号と用語との関係は次のとおりである。
P:有効電力[kW]
Q:電力用コンデンサ設置前の無効電力[kvar]
Qc:電力用コンデンサの容量[kvar]
θ:電力用コンデンサ設置前の力率角[°]
θ’:電力用コンデンサ設置後の力率角[°]
(b) 第2工場の受電端電圧を 6300[V]にするために設置する電力用コンデンサ容量[kvar]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、自家用変電所の送電端電圧は 6600[V]、専用配電線路の電線1線当たりの抵抗は 0.5[Ω]及びリアクタンスは 1[Ω]とする。
また、電力用コンデンサ設置前の負荷力率は 0.6(遅れ) とする。なお、配電線の電圧降下式は、簡略式を用いて計算するものとする。
(1) 700 (2) 900 (3) 1500 (4) 1800 (5) 2000
2012年(平成24年)問12 過去問解説
(a) コンデンサを設置すると、力率角は小さくなります。したがって、(2)が正解です。
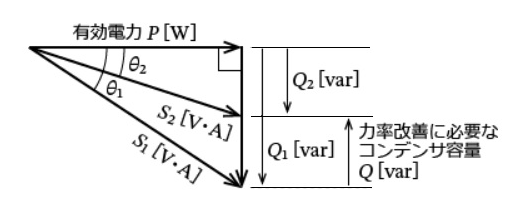
答え (2)
(b) コンデンサ設置前の皮相電力を $S_1$[kVA]、有効電力を $P_1$[kW]、無効電力を $Q_1$[kvar]とすると、
$S_1=\displaystyle \frac{ P_1}{cosθ_1 }=\displaystyle \frac{ 2000 }{0.6 }=3333.3[kVA]$
$Q_1=S_2sinθ=3333.3×0.8=2666.7[kvar]$
コンデンサ設置後の皮相電力を $S_2$[kVA]、有効電力を $P_2$[kW]、無効電力を $Q_2$[kvar]とすると、
$P_2=\sqrt{3}VrIcosθ$…(1)
$Q_2=\sqrt{3}VrIsinθ$…(2)
また、電圧降下の近似式より、
$Vs−Vr=\sqrt{3}I(rcosθ+xsinθ)$…(3)
(1),(2),(3)式より
$Vs−Vr=\displaystyle \frac{ P_2r}{Vr }+\displaystyle \frac{ Q_2x}{Vr }$
$6600−6300=\displaystyle \frac{ 2000×10^3×0.5}{6300 }+\displaystyle \frac{ Q_2×1}{6300 }$
これを計算すると、$ Q_2=890[kvar]$
求めるコンデンサ容量 $Q$[kvar]は、
$Q=Q_1-Q_2=2666.7-890≒1800[kvar]$
答え (4)
2015年(平成27年)問13
定格容量が 50kV・Aの単相変圧器3台をΔ‐Δ結線にし、一つのバンクとして、三相平衡負荷(遅れ力率 0.90 )に電力を供給する場合について、次の(a)及び(b)の問に答えよ。
(a) 図1のように消費電力 90kW(遅れ力率 0.90 )の三相平衡負荷を接続し使用していたところ、3台の単相変圧器のうちの1台が故障した。負荷はそのままで、残りの2台の単相変圧器をV‐V結線として使用するとき、このバンクはその定格容量より何[kV・A]過負荷となっているか。最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0 (2) 3.4 (3) 10.0 (4) 13.4 (5) 18.4
(b) 上記(a)において、故障した変圧器を同等のものと交換して 50kV・Aの単相変圧器3台をΔ‐Δ結線で復旧した後、力率改善のために、進相コンデンサを接続し、バンクの定格容量を超えない範囲で最大限まで三相平衡負荷(遅れ力率 0.90 )を増加し使用したところ、力率が 0.96(遅れ)となった。このときに接続されている三相平衡負荷の消費電力の値 [kW] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 135 (2) 144 (3) 150 (4) 156 (5) 167
2015年(平成27年)問13 過去問解説
(a)皮相電力を $S$[kVA]、有効電力を $P$[kW]とすると、
$S=\displaystyle \frac{ P}{cosθ }=\displaystyle \frac{ 90 }{0.9 }=100[kVA]$
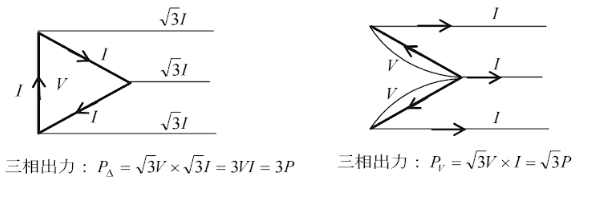
V結線の変圧器容量を $S_v$[kVA]とすると、変圧器1台の $\sqrt{3}$倍になりますので、
$S_v=\sqrt{3}×50=86.6[kVA]$
したがって、過負荷容量は
$100-86.6$=13.4[kVA]
答え (4)
(b) 3台のΔ結線で、進相コンデンサ挿入後の力率が 0.96 なので、有効電力 $P$[kW]は、
$P=3×50×0.96=144[kW]$
答え (2)





