このページでは、河川の流量と流況曲線について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された、河川の流量と流況曲線の過去問題も解説しています。
河川の流量と流況曲線
河川の流量
ある河川の流域全体に降った雨量のうち、どの程度が河川流量となって流出するのかを、降水量に対する河川流量の割合として流出係数で表しています。河川の年平均流量を Q［m3/s］は、以下の式で求めることができます。
$Q=\displaystyle \frac{ 年間流出水量 }{ 365日を秒単位に換算 }$
$=\displaystyle \frac{ kpA×10^3 }{ 365×24×60×60 }$［m3/s］
Q：河川の年平均流量［m3/s］
k：流出係数［％］
p：年間降水量［mm］
A：流域面積［km2］
流況曲線
水力発電所を設計する際、河川の流量と、どれだけの日数分その流量が利用できるのかを知っておく必要があります。そのため、流量の種別が定められており、この区分に従って河川流量が調査されます。
河川で利用することができる流量を縦軸に、期間ごとの日数を横軸にとり、流量の大きいものから順に並べたグラフを流況曲線といいます。
水力発電所で利用する流量と比較して、運転可能日数の算出や常時使用水量の決定、発電電力量や利用率の算定、必要な調整機能と日数の検討など、発電所の計画の際に利用されます。
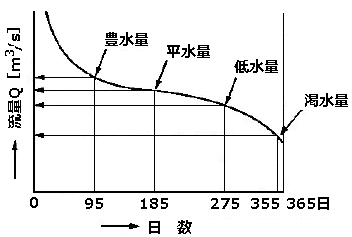
年間を通じて一定の日数以上、河川から得られる毎秒当たりの水量［m$^3$/s］の区分
(a) 渇水量：1年のうち 355日はこれより下らない流量
(b) 低水量：1年のうち 275日はこれより下らない流量
(c) 平水量：1年のうち 185日はこれより下らない流量
(d) 豊水量：1年のうち 95日はこれより下らない流量
河川の流量と流況曲線（例題）
例題１
流域面積 1000［km2］の水力発電所予定地点がある。年降水量を 2200［mm］、流出係数を 70［％］とすると、年間平均の流量［m3/ｓ］はいくらか。正しい値を次のうちから選べ。
(1) 5 (2) 16 (3) 28 (4) 49 (5) 60
例題１の解説
年間平均の流量 Q は
$\begin{eqnarray}Q&=&\displaystyle \frac{ 年間流出水量 }{ 365日を秒単位に換算 }\\\\&=&\displaystyle \frac{ kpA×10^3 }{ 365×24×60×60 }\\\\&=&\displaystyle \frac{ 0.7×2200×1000×10^3 }{ 31536000 }\\\\&=&\displaystyle \frac{15.4×10^8 }{ 31536000 }\\\\&≒&49［m^3/s］\end{eqnarray}$
答え (4)
例題２
河川流量の種別のうち、平水量とは1年のうち（ ア ）日これより下がらない流量をいい、豊水量とは１年のうち（ イ ）日これより下がらない流量をいう。
上記記述中の空白箇所（ア）,（イ）に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
(1) （ア）200 （イ）100
(2) （ア）200 （イ）95
(3) （ア）185 （イ）95
(4) （ア）185 （イ）75
(5) （ア）165 （イ）75
例題２の解説
河川流量の種別のうち、平水量とは1年のうち（ 185 ）日これより下がらない流量をいい、豊水量とは１年のうち（ 95 ）日これより下がらない流量をいう。
答え (3)
例題３
流域面積 250［km2］、年降水量を 1500［ｍｍ］、流出係数を 70［％］の水力地点がある。有効落差 40ｍとすれば、何kWの流込式発電所ができるか。最も近いのは次のうちどれか。
ただし、水車と発電機の総合効率は90％とし、流量は年間平均しているものとする。
(1) 2940 (2) 3150 (3) 8320 (4) 12000 (5) 29000
ヒント：発電機の出力 P ［kW］は
$P=9.8×流量(Q)×有効落差(H)×総合効率(η)［kW］$
例題３の解説
年間平均の流量 Q は
$\begin{eqnarray}Q&=&\displaystyle \frac{ 年間流出水量 }{ 365日を秒単位に換算 }\\\\&=&\displaystyle \frac{ kpA×10^3 }{ 365×24×60×60 }\\\\&=&\displaystyle \frac{ 0.7×1500×250×10^3 }{ 365×24×60×60 }\\\\&≒&8.32［m^3/s］\end{eqnarray}$
発電機の出力 P は
$\begin{eqnarray}P&=&9.8×流量(Q)×有効落差(H)×総合効率(η)\\\\&=&9.8×8.32×40×0.9\\\\&≒&2940［kW］\end{eqnarray}$
答え (1)
電験三種－電力（水力発電）過去問題
2008年（平成20年）問2
水力発電に関する記述として、誤っているのは次のうちどれか。
- 水管を流れる水の物理的性質を示す式として知られるベルヌーイの定理は、力学的エネルギー保存の法則に基づく定理である。
- 水力発電所には、一般的に短時間で起動・停止ができる、耐用年数が長い、エネルギー変換効率が高いなどの特徴がある。
- 水力発電は昭和30年代前半までわが国の発電の主力であった。現在では、国産エネルギー活用の意義があるが、発電電力量の比率が小さいため、水力発電の電力供給面における役割は失われている。
- 河川の1日の流量を年間を通して流量の多いものから順番に配列して描いた流況曲線は、発電電力量の計画において重要な情報となる。
- 水力発電所は落差を得るための土木設備の構造により、水路式、ダム式、ダム水路式に分類される。
2008年（平成20年）問2 過去問解説
- 正しい
- 正しい
- 誤り：水力発電は減少傾向にあるが、役割を失われるほどではない。
- 正しい
- 正しい
答え (3)
