第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「三相誘導電動機の理論と等価回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「三相誘導電動機の理論と等価回路」の過去問題も解説しています。
- 三相誘導電動機の理論
- 三相誘動電動機の等価回路
- 電験三種-機械の過去問解説:三相誘導電動機の理論と等価回路
- 1997年(平成9年)問12
- 1997年(平成9年)問12 過去問解説
- 1999年(平成11年)問3
- 1999年(平成11年)問3 過去問解説
- 2001年(平成13年)問2
- 2001年(平成13年)問2 過去問解説
- 2001年(平成13年)問3
- 2001年(平成13年)問3 過去問解説
- 2002年(平成14年)問3
- 2002年(平成14年)問3 過去問解説
- 2003年(平成15年)問3
- 2003年(平成15年)問3 過去問解説
- 2004年(平成16年)問15
- 2004年(平成16年)問15 過去問解説
- 2005年(平成17年)問3
- 2005年(平成17年)問3 過去問解説
- 2006年(平成18年)問16
- 2006年(平成18年)問16 過去問解説
- 2007年(平成19年)問4
- 2007年(平成19年)問4 過去問解説
- 2011年(平成23年)問3
- 2011年(平成23年)問3 過去問解説
- 2012年(平成24年)問4
- 2012年(平成24年)問4 過去問解説
- 2013年(平成25年)問4
- 2013年(平成25年)問4 過去問解説
- 2014年(平成26年)問4
- 2014年(平成26年)問4 過去問解説
- 2014年(平成26年)問6
- 2014年(平成26年)問6 過去問解説
- 2016年(平成28年)問3
- 2016年(平成28年)問3 過去問解説
- 2017年(平成29年)問3
- 2017年(平成29年)問3 過去問解説
三相誘導電動機の理論
同期速度
誘導電動機の固定子巻線に三相交流を流すと回転磁界が発生しますが、この回転磁界の回転速度のことを「同期速度」といいます。この同期速度は 周波数 $f$ や、固定子の極数 $p$ によって変わります。
同期速度を求める式
$n_s=\displaystyle\frac{120f}{p}$
$n_s$[min-1]:同期速度
$f$[Hz]:周波数
$p$:固定子の極数
三相誘導電動機の滑り
停止している3相の誘導電動機に三相交流電圧を加えると、回転子導体には大きな誘導電流 $I$[A]が流れ、トルク $T$ が生じて、回転子は回転します。その回転速度が増して、同期速度 $n_s$[min-1]に近づくと、回転子導体の電流は減少し、トルク $T$ は小さくなります。回転子の回転速度 $n$[min-1]は、同期速度 $n_s$ より小さく、$n_s$ に対する $n_s$ と $n$ の差を「滑り」 $s$ といいます。したがって、滑り $s$ は次の式で表すことができます。
滑りを求める式
$s=\displaystyle\frac{n_s-n}{n_s}$
$s$:滑り
$n_s$[min-1]:同期速度
$n$[min-1]:回転子の回転速度
滑り $s$ は、回転子が停止しているとき($π=0$)を 100% として、パーセントで表すことが多いです。全負荷(定格出力に相当する負荷)における $s$ の値は、小容量の電動機では 5~6% 程度、中・大容量の電動機では 6~10% 程度です。大容量の電動機は、機械的な負荷の変動に対する回転速度の変化が小さくなります。
回転速度を求める式①
$n=n_s(1-s)$
$n$[min-1]:回転子の回転速度
$n_s$[min-1]:同期速度
$s$:滑り
滑りを求める式 $s=\displaystyle\frac{n_s-n}{n_s}$ を変形させたものです。
回転速度を求める式②
$n=\displaystyle\frac{120f}{p}(1-s)$
$n$[min-1]:回転子の回転速度
$s$:滑り
$f$[Hz]:周波数
$p$:固定子の極数
回転速度を求める式① $n=n_s(1-s)$ に、同期速度を求める式 $n_s=\displaystyle\frac{120f}{p}$ を代入したものです。
誘導起電力
誘導電動機では、固定子巻線に励磁電流が流れると、回転磁界が生じ、これが回転子巻線を切るので、回転子巻線に起電力が誘導されます。それによって、回転子巻線に電流が流れます。その電流によって生じる起磁力を打ち消すように、固定子巻線に電流が流れ、固定子と回転子の間のエアギャップの磁束を一定に保ちます。ここで、固定子巻線を一次巻線、回転子巻線を二次巻線と考えると、変圧器と同じように電圧・電流の関係を取り扱うことができます。
なお、変圧器は電力を一次巻線から二次巻線に伝達するだけです。それに対して誘導電動機は、電力を機械的な出力に変換する働きをもっています。また、変圧器では、一次電流と二次電流の周波数は同じですが、誘導電動機では、それぞれの周波数が異なります。
- 回転子が停止しているとき
一次巻線に流れる励磁電流によって生じる回転磁界は、一次巻線を切るのと同じ速さで二次巻線を切るから、変圧器と同じように、一次巻線・二次巻線の各相には、一次誘導起電力 $E_1$ および二次誘導起電力 $E_2$ を生じます。
- 回転子が $n$[min-1]の速度で回転しているとき
回転磁界と回転子の相対速度は $n_s-n=sn_s$ で、回転子が停止しているときの $s$ 倍となります。したがって、運転中の二次誘導起電力 $E_2’$[V]および周波数 $f_2$[Hz]とも、停止時の $s$ 倍となります。
$E_2’=sE_2$
$f_2=sf_1$
ただし、$f_1$ は一次巻線に加えた電源の周波数で、 $f_2$ すなわち $sf_1$ は回転子巻線に流れる電流の周波数であり、「滑り周波数」といいます。

二次電流
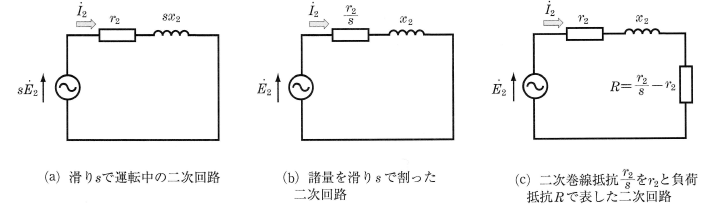
回転子巻線(二次巻線)の1相分の抵抗を $r_2$[Ω]、 1相分の漏れリアクタンスを $x_2$[Ω]とすると、滑り $s$ で運転している誘導電動機の二次誘導起電力は $sE_2$[V]、リアクタンスは $sx_2$[Ω]となるから、その回路は図2(a)のようになります。したがって、二次電流 $I_2$[A]は、次の式で表すことができます。
$I_2=\displaystyle\frac{sE_2}{\sqrt{{r_2}^2+(sx_2)^2}}$
上式を変形すると次のようになります。
$I_2=\displaystyle\frac{E_2}{\sqrt{\left(\displaystyle\frac{r_2}{s}\right)^2+{x_2}^2}}$
上式に基づく回路は、図2(b)のようになります。
誘導電動機の回転子巻線抵抗は、静止状態では $r_2$ ですが、回転速度により、$\displaystyle\frac{r_2}{s}$ に変化します。この増加した抵抗分 $R=\displaystyle\frac{r_2}{s}-r_2$ は誘導電動機の負荷抵抗分と考えられます。この関係を表した回路が図2(c)です。
誘導電動機の負荷抵抗 $R=\displaystyle\frac{r_2}{s}-r_2$ は、変圧器の負荷抵抗に相当すると考えれば、誘導電動機も変圧器と同様に取り扱うことができます。
コイルに電流を流すとコイルの中に磁束が発生します。この時コイルの外にも磁束は発生しています。このコイルの外に発生する磁束を漏れ磁束といいます。このとき、漏れ磁束によりコイルに誘導性リアクタンスが発生します。この誘導性リアクタンスのことを「漏れリアクタンス」といいます。
一次電流
二次電流 $I_2$[A]が流れると、$I_2$[A]によって生じる回転磁界が一次側の回転磁界を打ち消すように作用します。そのため、一次側に生じる電圧が減少し、一次負荷電流 ${I_1}’$[A]が流れます。そこで、一次巻線と二次巻線の巻数比を $α$ とすると、$I_2$[A]と ${I_1}’$[A]との間には、次の関係がなりたちます。
${I_1}’=\displaystyle\frac{1}{α}I_2$
また、一次電流 $\dot {I}_1$[A]は、一次巻線に流れる励磁電流 $\dot{I}_o$[A]と、一次負荷電流 $\dot {I}_1’$[A]とのベクトルの和になります。つまり、$\dot {I}_1=\dot{I}_o+\dot {I}_1’$ です。
三相誘動電動機の等価回路
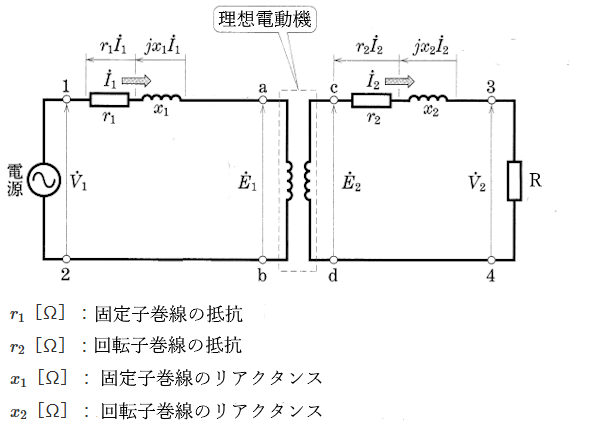
理想的な三相誘動電動機
巻線に発生する抵抗損や漏れ磁束による漏れリアクタンスなどが全く無く、一次巻線の電圧電流を全て二次巻線に伝えることのできる三相誘導電動機のことを「理想的な三相誘動電動機」といいます。
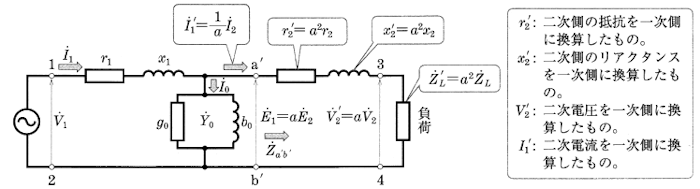
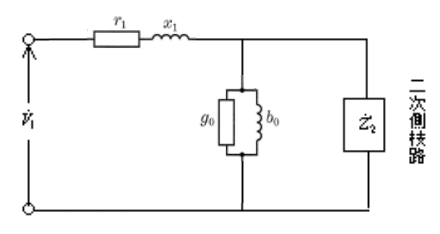
実際の電動機には、巻線に発生する抵抗損や漏れ磁束による漏れリアクタンスがあります。それらの損失を電動機から切り離して、理想的な三相誘動電動機の外部に、固定子・回転子巻線の抵抗 $r_1$[Ω],$r_2$[Ω]、固定子・回転子巻線の漏れリアクタンス $x_1$[Ω],$x_2$[Ω]を接続した等価回路は、図3のように考えることができます。
励磁回路
三相誘動電動機の滑りによる抵抗 $R$ をゼロにして、一次側に電圧を加えたときに流れる電流を励磁電流 $\dot{I}_o$ といいます。励磁電流は、磁束を作る磁化電流と鉄損を発生させる鉄損電流からできています。この励磁回路を図4で表すと次のようになります。
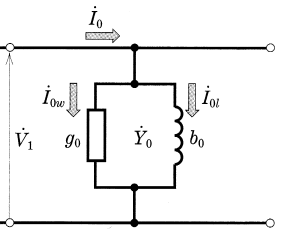
$\dot{I}_o$[A]:励磁電流
$g_o$[S]:励磁コンダクタンス
$b_o$[S]:励磁サセプタンス
$\dot{Y}_o$[S]:励磁アドミタンス
コンダクタンス $G$
抵抗 $R$ の逆数です。電流の流れやすさを表しています。単位は[S](読み:ジーメンス)を用います。
サセプタンス $B$
リアクタンス $X$ の逆数です。電流の流れやすさを表しています。単位は[S]を用います。
アドミタンス $Y$
インピーダンス $Z$ の逆数です。電流の流れやすさを表しています。単位は[S]を用います。アドミタンス $Y$ はコンダクタンス $G$ とサセプタンス $B$ を合わせたもので、式は $Y=G+jB$ と表します。アドミタンスの実数部がコンダクタンス $G$ で、虚数部がサセプタンス $B$ となります。
誘導電動機の等価回路
図4の励磁回路を、図3の理想等価回路に組み込んだ回路を等価回路(図5)といいます。図は誘導電動機の1相分を表しています。
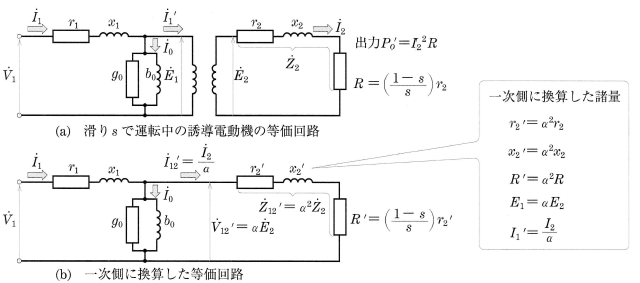
図5(a)の回路の電圧・電流およびインピーダンスなどを計算する場合、誘動電動機の部分を取り外し、単一電気回路として考えると便利です。この目的のために図5(b)の回路に置き換え、電気的に等価になる条件を考えます。
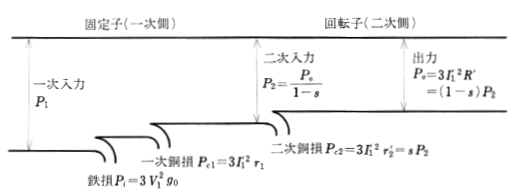
図5で、1相分の二次入力を ${P_2}’$[W]、二次銅損を ${P_{c_2}}’$[W]、出力を ${P_o} ‘$[W]とすると、次の式がなりたちます。
${P_2}’={I_2}^2\displaystyle\frac{r_2}{s}=\displaystyle\frac{ {P_{c2}}’ }{s}$
$\begin{eqnarray}{P_o}’&=&{P_2}’-{I_2}^2r_2\\\\&=&{P_2}’-{P_{c_2}}’\\\\&=&{P_2}’-s{P_2}’\\\\&=&(1-S){P_2}’\end{eqnarray}$
また、出力 ${P_o} ‘$[W]は、次の式のようにも表わすことができます。
$\begin{eqnarray}{P_o} ‘&=&{I_2}^2\displaystyle\frac{r_2}{s}-{I_2}^2r_2\\\\&=&{I_2}^2r_2\left(\displaystyle\frac{1-s}{s}\right)\\\\&=&{I_2}^2R\end{eqnarray}$
ここで、$R$[Ω]は機械的な負荷を表す等価抵抗で、$\displaystyle\frac{r_2}{s}$[Ω]は二次抵抗 $r_2$[Ω]と $R$[Ω]の和です。それで、$R$[Ω]を用いて等価回路を図示すると、図5(a)のように表すことができます。図5(a)の二次側の諸量を一次側に換算すると、次のようになります。
${V_{12}}’=E_1=αE_2$
${I_{12}}’={I_1}’=\displaystyle\frac{I_2}{α}$
${Z_{12}}’=\displaystyle\frac{{V_{12}}’}{{I_{12}}’}=\displaystyle\frac{αE_2}{\displaystyle\frac{I_2}{α}}=α^2Z_2$
以上のことから、図5(a)は図5(b)の回路で表すことができます。
二次側の諸量を一次側に換算する方法
- 電圧:$a$倍
- 電流:$\displaystyle\frac{1}{a}$倍
- インピーダンス:$a^2$倍
簡易等価回路における諸量の計算
図6は、図5の励磁回路を電源側に移したものですが、計算誤差は小さく、しかも計算が簡単になるので、ふつうこの簡易等価回路が用いられます。
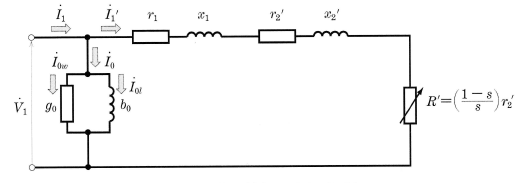
図6の簡易等価回路は1相分を表していますが、三相回路は単相回路を三つ組み合わせたものですので、鉄損・一次銅損・一次入力・二次入力・二次銅損・出力などの値は、それぞれ1相分の値の3倍になります。
図6において、三相誘導電動機の3相分の諸量を求めると、次のようになります。ただし、$V_1$ は一次相電圧、$θ_1$ は $\dot{V}_1$ と $\dot{I}_1$ の位相差です。
一次負荷電流
${I_1}’=\displaystyle\frac{V_1}{\sqrt{\left(r_1+\displaystyle\frac{{r_2}’ }{s}\right)^2 +(x_1+{x_2}’)^2}}$[A]
励磁電流
$I_o=V_1\sqrt{{g_o}^2+{b_o}^2}$[A]
一次電流
$\dot{I}_1=\dot{I}_o+{\dot{I}_1}’$[A]
一次入力を求める式
$\begin{eqnarray}P_1&=&P_i+P_{c1}+P_{c2}+P_o\\\\&=&3V_1I_1cosθ_1\\\\&=&\sqrt{3}V_nI_lcosθ_1\end{eqnarray}$
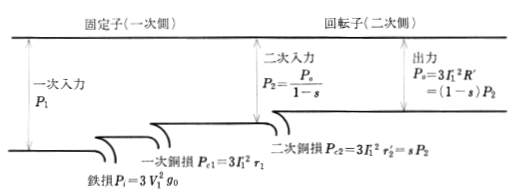
$P_1$[W]:一次入力
$P_i$[W]:鉄損
$P_{c1}$[W]:一次銅損
$P_{c2}$[W]:二次銅損
$P_o$[W]:出力
$V_1$[V]:一次相電圧
$I_1$[A]:一次電流
$V_n$[V]:定格電流
$I_l$[A]:線電流
二次入力を求める式
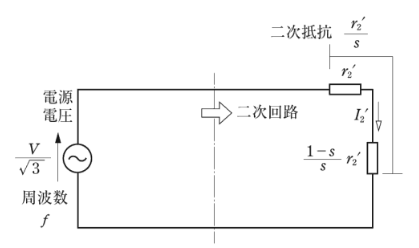
$\begin{eqnarray}P_2&=&P_{c2}+P_o=\displaystyle\frac{P_o}{1-s}\\&=&3{{I_1}’}^2\displaystyle\frac{{r_2}’}{s}\end{eqnarray}$
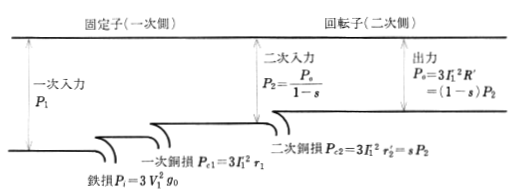
$P_2$[W]:二次入力
$P_{c2}$[W]:二次銅損
$P_o$[W]:出力
$s$:滑り
${I_1}’$[A]:一次換算負荷電流
${r_2}’$[Ω]:一次換算二次抵抗
二次入力、二次銅損、二次出力の比の関係式
$P_2:P_{c2}:P_o=1:s:(1-s)$
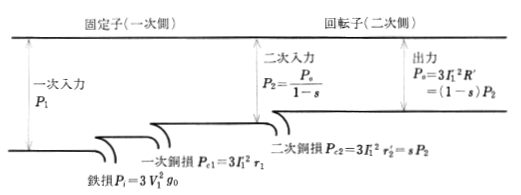
$P_2$[W]:二次入力
$P_{c2}$[W]:二次銅損
$P_o$[W]:出力
$s$:滑り
鉄損を求める式
$P_i=3V_1I_{ow}=3{V_1}^2g_o$
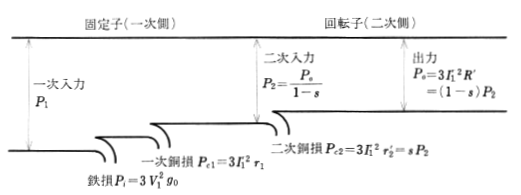
$P_i$[W]:鉄損
$I_{ow}$[A]:励磁コンダクタンス電流
$V_1$[V]:一次相電圧
$g_o$[S]:励磁コンダクタンス
一次銅損・二次銅損を求める式
一次銅損:$P_{c1}=3{{I_1}’}^2r_1$[W]
二次銅損:$P_{c2}=3{{I_1}’}^2{r_2}’=sP_2$

$P_{c1}$[W]:一次銅損
$P_{c2}$[W]:二次銅損
${I_1}’$[A]:一次換算負荷電流
$r_1$[Ω]:一次抵抗
${r_2}’$[Ω]:一次換算二次抵抗
$s$:滑り
$P_2$[W]:二次入力
出力を求める式
$\begin{eqnarray}P_o&=&3{{I_1}’}^2R’\\\\&=&3{{I_1}’}^2\left(\displaystyle\frac{1-s}{s}\right){r_2}’\\\\&=&(1-s)P_2\\\\&=&ωT\end{eqnarray}$
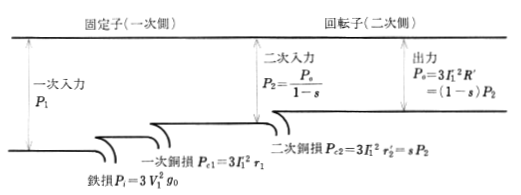
$P_o$[W]:出力
${I_1}’$[A]:一次換算負荷電流
$R’$[Ω]:一次換算負荷抵抗
$s$:滑り
$ω=\displaystyle\frac{2πn}{60}$[rsd/s]:角速度
$T$[N・m]:トルク
同期ワットを求める式
$P_2=\displaystyle\frac{2πn_sT}{60}$
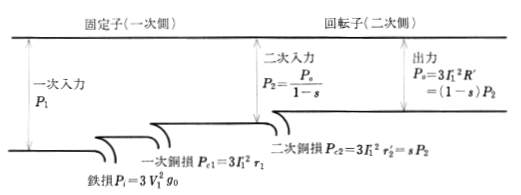
$P_2$[W]:二次入力
$n_s$[min-1]:同期速度
$T$[N・m]:トルク
誘導電動機の二次入力のことを「同期ワット」といいます。同期ワットの式は、分子が回転速度 $n$ ではなく同期速度 $n_s$ になります。
二次効率を求める式
$η_o=\displaystyle\frac{P_o}{P_2}=\displaystyle\frac{(1-s)P_2}{P_2}=1-s$
$η_o$:二次効率
$P_o$[W]:出力
$P_2$[W]:二次入力
$s$:滑り
電動機の効率を求める式
$η=\displaystyle\frac{P_o}{P_1}$
$η$:電動機効率
$P_o$[W]:出力
$P_1$[W]:一次入力
電験三種-機械の過去問解説:三相誘導電動機の理論と等価回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問12
定格出力 200[kW]、定格電圧 3000[V]、周波数 50[Hz]、8極のかご形三相誘導電動機がある。全負荷時の二次銅損は 6[kW]、機械損は 4[kW]である。この電動機の全負荷時の回転速度[rpm]として、正しいのは次のうちどれか。ただし、定格出力は定格負荷時の機械出力(発生動力)から機械損を引いたものに等しいものとする。
(1) 714 (2) 721 (3) 729 (4) 736 (5) 750
1997年(平成9年)問12 過去問解説
定格出力を $P$[kW]、機械損を $P_m$[kW]、全負荷時の二次銅損を $P_{c2}$[kW]とすると、二次入力 $P_2$[W]は、
$P_2=P+P_m+P_{c2}=200+4+6=210$[kW]
すべりを $s$ とすると、二次銅損は、$P_{c2}=3{{I_1}’}^2{r_2}’=sP_2$[W]より、
$6=s×210$
$s=\displaystyle\frac{6}{210}$
同期速度を $n_s$[rpm]とすると、
$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×50}{8}=750$[rpm]
回転速度は、$s=\displaystyle\frac{同期速度-回転速度}{同期速度}=\displaystyle\frac{n_s-n}{n_s}$ なので、
$\displaystyle\frac{6}{210}=\displaystyle\frac{750-n}{750}$
$n=750×(1-\displaystyle\frac{6}{210})=729$[rpm]
答え (3)
1999年(平成11年)問3
三相誘導電動機が滑り 3[%]で運転している。このとき、電動機の二次銅損が 147[W]であるとすると、電動機出力[kW]の値として、正しいのは次のうちどれか。ただし、機械損は無視するものとする
(1) 4.2 (2) 4.5 (3) 4.8 (4) 5.1 (5) 5.4
1999年(平成11年)問3 過去問解説
出力を $P_o$[W]、二次銅損を $P_{c2}$[W]、二次入力を $P_2$[W]、すべりを $s$ とすると、
$P_{c2}=sP_2$
$P_o=(1-s)P_2$
$P_o=\displaystyle\frac{1-s}{s}×P_{c2}=\displaystyle\frac{1-0.03}{0.03}×147=4.8$[kW]
答え (3)
2001年(平成13年)問2
定格電圧 200[V]、定格電流 9[A]の三相かご形誘導電動機があり、端子電圧が 200[V]のときに始動電流は定格電流の 600[%]である。この電動機をある電源に接続して始動したところ、その電源の内部インピーダンスにより、電動機の端子電圧が 180[V]になった。このときの電動機の始動電流[A]の値として、最も近いのは次のうちどれか。
(1) 44 (2) 49 (3) 54 (4) 60 (5) 67
2001年(平成13年)問2 過去問解説
端子電圧が 200[V]の時の相電圧は $\displaystyle\frac{200}{\sqrt{3}}$[V]で、このときの始動電流を $I$ [A]は、定格電流の600[%]ですので、インピーダンスを $Z$[Ω]とすると、
$E=IZ$
$\displaystyle\frac{200}{\sqrt{3}}=9×6×Z$
$Z=2.14$[Ω]
端子電圧が180[V]のときの始動電流を $I_a$[A]とすると、
$180=I_a×2.14$
$I_a≒49$[A]
答え (2)
2001年(平成13年)問3
三相かご形誘導電動機があり、滑りsで回転している。このとき、かご形回転子の導体中に発生する誘導起電力の大きさは停止時の( ア )倍であり、この誘導起電力の周波数は停止時の( イ )倍である。このことから、図のような誘導電動機の星形一次換算1相分の等価回路において、二次側枝路のインピーダンス ${Z_2}’$ は( ウ )になる。
ただし、${r_2}’$ は一次換算1相分の二次抵抗、${x_2}’$ は一次換算1相分の二次漏れリアクタンスとする。
上記の記述中の空白の(ア),(イ)及び(ウ)に記入する記号又は式として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | s | s | ${r_2}’+j\displaystyle\frac{ {x_2}’ }{s}$ |
| (2) | $\displaystyle\frac{1}{s}$ | s | $\displaystyle\frac{{r_2}’ }{s}+js{x_2}’$ |
| (3) | $\displaystyle\frac{1}{s}$ | $\displaystyle\frac{1}{s}$ | ${r_2}’+j\displaystyle\frac{ {x_2}’ }{s}$ |
| (4) | s | $\displaystyle\frac{1}{s}$ | ${r_2}’+j\displaystyle\frac{ {x_2}’ }{s}$ |
| (5) | s | s | $\displaystyle\frac{{r_2}’ }{s}+j{x_2}’$ |
2001年(平成13年)問3 過去問解説
三相かご形誘導電動機があり、滑りsで回転している。このとき、かご形回転子の導体中に発生する誘導起電力の大きさは停止時の( s )倍であり、この誘導起電力の周波数は停止時の( s )倍である。このことから、図のような誘導電動機の星形一次換算1相分の等価回路において、二次側枝路のインピーダンス ${Z_2}’$ は( $\displaystyle\frac{{r_2}’ }{s}+j{x_2}’$ )になる。
回転子が停止しているとき
一次巻線に流れる励磁電流によって生じる回転磁界は、一次巻線を切るのと同じ速さで二次巻線を切るから、変圧器と同じように、一次巻線・二次巻線の各相には、一次誘導起電力 $E_1$ および二次誘導起電力 $E_2$ を生じます。
回転子が n[min-1]の速度で回転しているとき
回転磁界と回転子の相対速度は $n_s-n=sn_s$ で、回転子が停止しているときの $s$ 倍となります。したがって、運転中の二次誘導起電力 $E_2’$[V]および周波数 $f_2$[Hz]とも、次の式に示すように、停止時の $s$ 倍となります。
$E_2’=sE_2$
$f_2=sf_1$
停止時の回転体導体の起電力を ${E_2}’$ とすると、回転子電流 ${I_2}’$ は、
${I_2}’=\displaystyle\frac{s {E_2}’ }{{r_2}’+js{x_2}’}=\displaystyle\frac{s {E_2}’ }{\displaystyle\frac{{r_2}’}{s}+j{x_2}’}$
したがって、一次側に変換した等価回路における二次側枝路のインピーダンス ${Z_2}’$ は、
${Z_2}’=\displaystyle\frac{{r_2}’}{s}+j{x_2}’$
となります。
答え (5)
2002年(平成14年)問3
三相誘導電動機があり、回転子の巻線抵抗 $r_2= 0.14$[Ω]である。この電動機が滑りs=4[%]、回転子の電流 $I_2=12$[A]で運転しているとき、1相当たりの回転子入力 $P_2$[W]の値として、正しいのは次のうちどれか。 ただし、$r_2$ 及び $I_2$ は星形一次換算した1相分の値である。
(1) 20 (2) 42 (3) 465 (4) 484 (5) 504
2002年(平成14年)問3 過去問解説
回転子入力 $P_2$[W]は、
${P_2}={I_2}^2\displaystyle\frac{r_2}{s}={12}^2×\displaystyle\frac{0.14}{0.04}=504$[W]
答え (5)
2003年(平成15年)問3
三相誘導電動機があり、負荷を負って滑り 5[%]で運転している。1相当たりの二次電流が 12[A]のとき、1相当たりの電動機一次入力[W]の値として、最も近いのは次のうちどれか。ただし、この電動機の1相当たりの二次抵抗は 0.08[Ω]、1相当たりの鉄損は 10[W]であり、一次銅損は二次銅損の2倍とする。
(1) 208 (2) 219 (3) 230 (4) 240 (5) 263
2003年(平成15年)問3 過去問解説
1相当たりの一次入力を $P_1$[W]、一次銅損を $P_{c1}$[W]、鉄損を $P_i$[W]、二次銅損を $P_{c2}$[W]とすると、
$P_1=P_{c1}+P_i+P_{c2}$
1相当たりの二次入力を $P_2$[W]、すべりを $s$、1相当たりの二次抵抗を $r_2$[Ω]、二次電流を $I_2$[A]とすると、
$P_2={I_2}^2×\displaystyle\frac{r}{s}=12^2×\displaystyle\frac{0.08}{0.05}=230.4$[W]
$P_{c2}=sP_2=0.05×230.4=11.5$[W]
$P_{c1}=2P_{c2}=23$[W]
したがって、
$P_1=P_{c1}+P_i+P_{c2}=23+10+230.4=263.4$[kW]
答え (5)
2004年(平成16年)問15
定格出力 15[kW]、定格周波数 60[Hz]、4極の三相誘導電動機があり、トルク一定の負荷を負って運転している。この電動機について、次の(a)及び(b)に答えよ。
(a) 定格回転速度 1746[min-1]で運転しているときの滑り周波数[Hz]の値として、正しいのは次のうちどれか。
(1) 1.50 (2) 1.80 (3) 1.86 (4) 2.10 (5) 2.17
(b) インバータにより一次周波数制御を行って、一次周波数を 40[Hz]としたときの回転速度[min-1]として、正しいのは次のうちどれか。ただし、滑り周波数は一次周波数にかかわらず常に一定とする。
(1) 1146 (2) 1164 (3) 1433 (4) 1455 (5) 1719
2004年(平成16年)問15 過去問解説
(a) 同期速度を $n_s$[min-1]とすると、
$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×60}{4}=1800$[min-1]
回転速度を $n$[min-1]とすると、すべり $s$ は、
$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{1800-1746}{1800}=0.03$
滑り周波数は、$f_2=sf_1$[Hz]ですので、
$sf_1=0.03×60=1.80$[Hz]
答え (2)
(b) 回転子は 40-1.8=38.2[Hz]の同期速度で回転することになりますので、
$n_s=\displaystyle\frac{120×38.2}{4}=1146$[min-1]
答え (1)
2005年(平成17年)問3
誘導電動機が滑り $s$ で運転しているとき、二次銅損 $P_{c2}$[W]の値は二次入力 $P_2$[W]の( ア )倍となり、機械出力 $P_m$[W]の値は二次入力 $P_2$[W]の( イ )倍となる。また、滑り $s$ が1のとき、この誘導電動機は( ウ )の状態にあり、このときの機械出力の値は $P_m=$( エ )[W]となる。
上記の記述中の空白の(ア),(イ),(ウ)及び(エ)に記入する語句、式又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | $s$ | $1-s$ | 同期速度 | $P_2-P_{c2}$ |
| (2) | $1-s$ | $s$ | 同期速度 | $P_2$ |
| (3) | $\displaystyle\frac{1}{s}$ | $\displaystyle\frac{1}{1-s}$ | 停止 | $P_2-P_{c2}$ |
| (4) | $\displaystyle\frac{1}{s}$ | $\displaystyle\frac{s-1}{s}$ | 停止 | 0 |
| (5) | $s$ | $1-s$ | 停止 | 0 |
2005年(平成17年)問3 過去問解説
誘導電動機が滑り $s$ で運転しているとき、二次銅損 $P_{c2}$[W]の値は二次入力 $P_2$[W]の( $s$ )倍となり、機械出力 $P_m$[W]の値は二次入力 $P_2$[W]の( $1-s$ )倍となる。また、滑り $s$ が1のとき、この誘導電動機は( 停止 )の状態にあり、このときの機械出力の値は $P_m=$( 0 )[W]となる。
滑り $s$ が1と言うことは「停止」の状態を示しています。したがって、$s=1$ なら、機械出力が 0 となります。ただし、銅損は電圧が加わっているので 0 にはななりません。
二次銅損、二次入力、機械出力を式で表わすと、
二次銅損 $P_{c2}=3{{I_1}’}^2{r_2}’=sP_2$[W]
二次入力 $P_2=3{{I_1}’}^2\displaystyle\frac{{r_2}’}{s}=P_{c2}+P_o=\displaystyle\frac{P_o}{1-s}$[W]
出力 $P_o=3{{I_1}’}^2R’=3{{I_1}’}^2\left(\displaystyle\frac{1-s}{s}\right){r_2}’=(1-s)P_2$[W]
したがって、二次入力:二次銅損:機械出力=1:s:(1-s) の関係にあります。
答え (5)
2006年(平成18年)問16
三相かご形誘導電動機を周波数 60[Hz]の電源に接続して運転したとき、機械出力は 34.8[kW]、滑りは 3[%]、固定子の銅損(一次銅損)は 3.8[kW]、鉄損は 1.4[kW]であった、この電動機について、次の(a)及び(b)に答えよ。
ただし、機械損は無視できるものとする。
(a) この運転時の回転子の銅損(二次銅損)[kW]の値として、最も近いのは次のうちどれか。
(1) 0.89 (2) 0.93 (3) 1.08 (4) 1.16 (5) 1.20
(b) この運転時の一次入力[kW]の値として、最も近いものはどれか。
(1) 40.2 (2) 41.1 (3) 42.2 (4) 43.5 (5) 44.8
2006年(平成18年)問16 過去問解説
(a) 二次入力を $P_2$[kW]、機械出力を $P_o$[kW]とすると、二次銅損 $P_{c2}$[kW]は、
$P_o=(1-s)P_2$
$P_{c2}=sP_2=\displaystyle\frac{s}{1-s}P_o=\displaystyle\frac{0.03}{1-0.03}×34.8=1.08$[kW]
答え (3)
(2) 鉄損を $P_i$[kW]、一次銅損を $P_{c1}$[kW]とすると、一次入力 $P_1$[kW]は、
$P_1=P_i+P_{c1}+P_{c2}+P_o$
$=1.4+3.8+1.08+34.8≒41.1$[kW]
答え (2)
2007年(平成19年)問4
$V/f$ 一定制御インバータで駆動されている6極の誘導電動機がある。この電動機は、端子電圧を $V$[V]、周波数を $f$[Hz]として、$V/f$比=4 一定制御インバータによって 66[Hz]で駆動されている。
このときの滑りは 5[%]であった。この誘導電動機の回転速度[min-1]として、正しいのは次のうちどれか。
(1) 1140 (2) 1200 (3) 1254 (4) 1320 (5) 1710
2007年(平成19年)問4 過去問解説
同期速度を $n_s$[min-1]とすると、
$n_s=\displaystyle\frac{120f}{p}=\displaystyle\frac{120×66}{6}=1320$[min-1]
回転速度を $n$[min-1]とすると、滑り $s$ は 5[%]ですので、
$s=\displaystyle\frac{n_s-n}{n_s}$
$\displaystyle\frac{5}{100}=\displaystyle\frac{1320-n}{1320}$
$n=(1-0.05)×1320=1254$[min-1]
答え (3)
2011年(平成23年)問3
次の文章は, 巻線形誘導電動機に関する記述である。
三相巻線形誘導電動機の二次側に外部抵抗を接続して、 誘導電動機を運転することを考える。 ただし、外部抵抗は誘導電動機内の二次回路にある抵抗に比べて十分大きく、誘導電動機内部の鉄損、銅損及び一次、二次のインダクタンスなどは無視できるものとする。
いま、回転子を拘束して、一次電圧 $V_1$ として 200[V]を印加したときに二次側の外部抵抗を接続した端子に現れる電圧 $V_{2s}$ は 140[V]であった。拘束を外して始動した後に回転速度が上昇し、同期速 1500[min-1]に対して 1200[min-1]に到達して、負荷と釣り合ったとする。
このときの一次電圧 $V_1$ は 200[V]のままであると、二次側の端子に現れる電圧 $V_2$ は( ア )[V]となる。
また、機械負荷に $P_m$[W]が伝達されるとすると、一次側から供給する電力 $P_1$[W]、外部抵抗で消費される電力 $P_{2c}$[W]との関係は次式となる。
$P_1=P_m+$( イ )$×P_{2c}$
$P_{2c}=$( ウ )$×P_1$
したがって、$P_{2c}$ と $P_m$ の関係は次式となる。
$P_{2c}=$( エ )$×P_m$
接続する外部抵抗には、このような運転に使える電圧・容量の抵抗器を選択しなければならない。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 112 | 0.8 | 0.8 | 0.25 |
| (2) | 28 | 1 | 0.2 | 4 |
| (3) | 28 | 1 | 0.2 | 0.25 |
| (4) | 112 | 0.8 | 0.8 | 4 |
| (5) | 112 | 1 | 0.2 | 0.25 |
2011年(平成23年)問3 過去問解説
回転速度を $n$[min-1]、同期速度を $n_s$[min-1]とすると、滑り $s$ は 、
$s=\displaystyle\frac{n_s-n}{n_s}=\displaystyle\frac{1500-1200}{1500}=0.2$
二次側の端子に現れる電圧 $V_2$[V]は、
$V_2=sV_{2s}=0.2×140=28$[V]… (ア)
一次側から供給する電力(一次入力) $P_1$[W]、二次入力 $P_2$[W]、外部抵抗で消費される電力(二次銅損) $P_{2c}$ [W]、機械負荷(出力)に $P_m$[W]との関係は
$P_1=P_2=P_{2c}+P_m$
$P_1=P_{2c}+1×P_m$ … (イ)
$P_{2c}=sP_2=0.2P_2=0.2×P_1$ … (ウ)
$P_{2c}=0.2×P_1=0.2(P_{2c}+P_m)$
$P_{2c}=0.25P_m$ … (エ)
答え (3)
2012年(平成24年)問4
三相誘導電動機があり、一次巻線抵抗が 15[Ω]、一次側に換算した二次巻線抵抗が 9[Ω]、滑りが 0.1 のとき、効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、励磁電流は無視できるものとし、損失は、一次巻線による銅損と二次巻線による銅損しか存在しないものとする。
(1) 75 (2) 77 (3) 79 (4) 82 (5) 85
2012年(平成24年)問4 過去問解説
効率 $η$[%]は、$\displaystyle\frac{出力}{入力}×100$で、求めることができます。一次入力を $P_1$[W]、機械出力を $P_o$[W]とし、一次銅損 $P_{c1}$[W]、二次銅損 $P_{c2}$[W]すると、
$P_1=P_{c1}+P_{c2}+P_o$
$η=\displaystyle\frac{P_o}{P_1}×100=\displaystyle\frac{P_o}{P_{c1}+P_{c2}+P_o}×100$
と表わすことができます。二次入力を $P_2$[W]、滑りが 0.1ですので、
$P_{c2}=sP_2=0.1P_2$[W]
$P_o=(1-s)P_2=(1-0.1)P_2=0.9P_2$
$P_o=0.9×\displaystyle\frac{P_{c2}}{0.1}$
$P_{c2}=\displaystyle\frac{1}{9}P_o$
一次負荷電流を ${I_1}’$、一次巻線抵抗を $r_1$[Ω]、一次側に換算した二次巻線抵抗を ${r_2}’$[Ω]とすると、
一次銅損
$P_{c1}=3{{I_1}’}^2r_1=3{{I_1}’}^2×15$[W]
二次銅損
$P_{c2}=3{{I_1}’}^2{r_2}’=3{{I_1}’}^2×9$[W]
したがって、
$\displaystyle\frac{15}{P_{c1}}=\displaystyle\frac{9}{P_{c2}}$
$P_{c1} =\displaystyle\frac{15}{9}P_{c2}=\displaystyle\frac{15}{9}×\displaystyle\frac{1}{9}P_o=\displaystyle\frac{5}{27}P_o$
効率 $η$[%]は、
$η=\displaystyle\frac{P_o}{P_{c1}+P_{c2}+P_o}×100$
$=\displaystyle\frac{P_o}{\displaystyle\frac{5}{27}P_o+\displaystyle\frac{1}{9}P_o+P_o}×100≒77$[%]
答え (2)
2013年(平成25年)問4
二次電流一定(トルクがほぼ一定の負荷条件)で運転している三相巻線形誘導電動機がある。滑り 0.01 で定格運転しているときに、二次回路の抵抗を大きくしたところ、二次回路の損失は 30 倍に増加した。電動機の出力は定格出力の何[%]になったか、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 10 (2) 30 (3) 50 (4) 70 (5) 90
2013年(平成25年)問4 過去問解説
滑り 0.01 で定格運転しているときの二次銅損を $P_{2c}$[W]、出力を $P_o$[W]とすると、
$P_{2c}=sP_2=0.01P_2$[W]
$P_o=(1-s)P_2=(1-0.01)P_2=0.99P_2$[W]
二次回路の損失が 30 倍に増加したときは、すべりも 30 倍になります。二次銅損を ${P_{2c}}’$[W]、出力を ${P_o}’$[W]とすると、
${P_{2c}}’=30P_{2c}=0.3P_2$[W]
${P_o}’=(1-0.3)P_2=0.7P_2$[W]
したがって、求める答えは
$\displaystyle\frac{{P_o}’}{P_o}=\displaystyle\frac{0.7P_2}{0.99P_2}≒0.7$(70%)
答え (4)
2014年(平成26年)問4
一般的な三相かご形誘導電動機がある。
出力が大きい定格運転条件では、誘導機の等価回路の電流は、「二次電流≫励磁電流」であるから、励磁回路を省略しても特性をほぼ表現できる。さらに、「二次抵抗による電圧降下≫その他の電圧降下」となるので、一次抵抗と漏れリアクタンスを省略しても、おおよその特性を検討できる。
このような電動機でトルク一定負荷の場合に、電流 100A の定格運転から電源電圧と周波数を共に10%下げて回転速度を少し下げた。このときの電動機の電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 80 (2) 90 (3) 100 (4) 110 (5) 120
2014年(平成26年)問4 過去問解説
励磁回路、一次抵抗、漏れリアクタンスを省略した1相分の一次換算等価回路を示します。
二次入力を $P_2$[W]、電源の角速度を $ω$[rad/s]、トルクを $T$[N・m]とし、3相分で考えると、
$P_2=ωT$[W]
$3×\displaystyle\frac{V}{\sqrt{3}}{I_2}’=ωT$[W]
$3×\displaystyle\frac{V}{\sqrt{3}}×100=ωT$[W] … (1)
電源電圧と周波数を共に10%下げたときの、電流を ${I_2}”$ とすると、
$3×\displaystyle\frac{V}{\sqrt{3}}×0.9×{I_2}”=0.9ωT$[W]
$3×\displaystyle\frac{V}{\sqrt{3}}×0.9×{I_2}”=0.9ωT$[W]
$3×\displaystyle\frac{V}{\sqrt{3}}×{I_2}”=ωT$[W]… (2)
トルクは一定ですので、式(1)=式(2)となります。したがって、
${I_2}”=100$[A]
答え (3)
2014年(平成26年)問6
次の文章は、三相誘導電動機の等価回路に関する記述である。
三相誘導電動機の1相当たりの等価回路は、( ア )と同様に表すことができ、その等価回路を使用することによって電圧 V 及び周波数 f を同時に変化させるインバータで運転したときの磁束、トルクの特性を検討することができる。
図の( イ )等価回路において、誘導電動機を例えば定格周波数、定格電圧の数パーセント程度の周波数、電圧で始動するときの特性を考える。この場合、もし始動電流が定格電流と同じだけ流れると、( ウ )による電圧降下の一次電圧に対する比率が定格時よりも大きくなるので、磁束が減少し、発生トルクが( エ )することが理解できる。また、誘導電動機を例えば定格周波数、定格電圧で運転するときは、上記電圧降下による計算誤差が小さく、計算が簡単になるので、励磁回路を図の( オ )側に移した簡易等価回路を使うことも有効である。この運転では、もしインバータが出力する電圧 V が減少したとしても、V/f 比を一定に保つように周波数fを減少させれば、負荷変動に影響されずに励磁電流がほぼ一定となることが分かる。
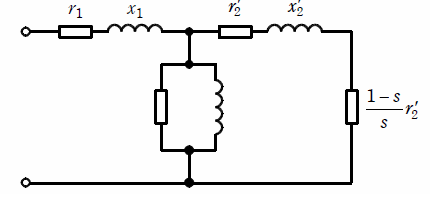
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 同期電動機 | L形 | 一次抵抗 | 増加 | 右端の負荷抵抗 |
| (2) | 変圧器 | T形 | 一次抵抗 | 減少 | 左端の端子 |
| (3) | 同期電動機 | T形 | 二次漏れリアクタンス | 減少 | 右端の負荷抵抗 |
| (4) | 変圧器 | L形 | 一次抵抗 | 増加 | 右端の負荷抵抗 |
| (5) | 変圧器 | T形 | 二次漏れリアクタンス | 減少 | 左端の端子 |
2014年(平成26年)問6 過去問解説
三相誘導電動機の1相当たりの等価回路は、( 変圧器 )と同様に表すことができ、その等価回路を使用することによって電圧 V 及び周波数 f を同時に変化させるインバータで運転したときの磁束、トルクの特性を検討することができる。
図の( T形 )等価回路において、誘導電動機を例えば定格周波数、定格電圧の数パーセント程度の周波数、電圧で始動するときの特性を考える。この場合、もし始動電流が定格電流と同じだけ流れると、( 一次抵抗 )による電圧降下の一次電圧に対する比率が定格時よりも大きくなるので、磁束が減少し、発生トルクが( 減少 )することが理解できる。また、誘導電動機を例えば定格周波数、定格電圧で運転するときは、上記電圧降下による計算誤差が小さく、計算が簡単になるので、励磁回路を図の( 左端の端子 )側に移した簡易等価回路を使うことも有効である。この運転では、もしインバータが出力する電圧 V が減少したとしても、V/f 比を一定に保つように周波数fを減少させれば、負荷変動に影響されずに励磁電流がほぼ一定となることが分かる。
答え (2)
2016年(平成28年)問3
次の文章は、三相誘導電動機の誘導起電力に関する記述である。
三相誘導電動機で固定子巻線に電流が流れると( ア )が生じ、これが回転子巻線を切るので回転子巻線に起電力が誘導され、この起電力によって回転子巻線に電流が流れることでトルクが生じる。この回転子巻線の電流によって生じる起磁力を( イ )ように固定子巻線に電流が流れる。
回転子が停止しているときは、固定子巻線に流れる電流によって生じる( ア )は、固定子巻線を切るのと同じ速さで回転子巻線を切る。このことは原理的に変圧器と同じであり、固定子巻線は変圧器の( ウ )巻線に相当し、回転子巻線は( エ )巻線に相当する。回転子巻線の各相には変圧器と同様に( エ )誘導起電力を生じる。
回転子が n[min-1]の速度で回転しているときは、( ア )の速度を $n_s$[min-1]とすると、滑り s は $s=\displaystyle\frac{n_s-n}{n_s}$ で表される。このときの( エ )誘導起電力の大きさは、回転子が停止しているときの( オ )倍となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 交番磁界 | 打ち消す | 二次 | 一次 | 1-s |
| (2) | 回転磁界 | 打ち消す | 一次 | 二次 | 1/s |
| (3) | 回転磁界 | 増加させる | 一次 | 二次 | s |
| (4) | 交番磁界 | 増加させる | 二次 | 一次 | 1/s |
| (5) | 回転磁界 | 打ち消す | 一次 | 二次 | s |
2016年(平成28年)問3 過去問解説
三相誘導電動機で固定子巻線に電流が流れると( 回転磁界 )が生じ、これが回転子巻線を切るので回転子巻線に起電力が誘導され、この起電力によって回転子巻線に電流が流れることでトルクが生じる。この回転子巻線の電流によって生じる起磁力を( 打ち消す )ように固定子巻線に電流が流れる。
回転子が停止しているときは、固定子巻線に流れる電流によって生じる( 回転磁界 )は、固定子巻線を切るのと同じ速さで回転子巻線を切る。このことは原理的に変圧器と同じであり、固定子巻線は変圧器の( 一次 )巻線に相当し、回転子巻線は( 二次 )巻線に相当する。回転子巻線の各相には変圧器と同様に( 二次 )誘導起電力を生じる。
回転子が n[min-1]の速度で回転しているときは、( 回転磁界 )の速度を $n_s$[min-1]とすると、滑り s は $s=\displaystyle\frac{n_s-n}{n_s}$ で表される。このときの( 二次 )誘導起電力の大きさは、回転子が停止しているときの( s )倍となる。
答え (5)
2017年(平成29年)問3
次の文章は、誘導機に関する記述である。
誘導機の二次入力は( ア )とも呼ばれ、トルクに比例する。二次入力における機械出力と二次銅損の比は、誘導機の滑りをsとして( イ )の関係にある。この関係を用いると、二次銅損は常に正であることから、s が-1から0の間の値をとるとき機械出力は( ウ )となり、誘導機は( エ )として運転される。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 同期ワット | (1-s):s | 負 | 発電機 |
| (2) | 同期ワット | (1+s):s | 負 | 発電機 |
| (3) | トルクワット | (1+s):s | 正 | 電動機 |
| (4) | 同期ワット | (1-s):s | 負 | 電動機 |
| (5) | トルクワット | (1-s):s | 正 | 電動機 |
2017年(平成29年)問3 過去問解説
誘導機の二次入力は( 同期ワット )とも呼ばれ、トルクに比例する。二次入力における機械出力と二次銅損の比は、誘導機の滑りを s として( (1-s):s )の関係にある。この関係を用いると、二次銅損は常に正であることから、s が-1から0の間の値をとるとき機械出力は( 負 )となり、誘導機は( 発電機 )として運転される。
答え (1)
電験三種の機械科目に出題される「誘導機」のページ
- 三相誘導電動機の原理と構造
- 三相誘導電動機の理論と等価回路
- 三相誘導電動機の特性
- 三相誘導電動機の運転






