第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「直流電動機の種類と特性」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「直流電動機の種類と特性」の過去問題も解説しています。
- 直流電動機のトルクと出力
- 逆起電力と回転速度
- 直流電動機の種類と特徴
- 電験三種-機械の過去問解説:直流電動機の種類と特性
- 1997年(平成9年)問10
- 1997年(平成9年)問10 過去問解説
- 1998年(平成10年)問12
- 1998年(平成10年)問12 過去問解説
- 2001年(平成13年)問12
- 2001年(平成13年)問12 過去問解説
- 2003年(平成15年)問1
- 2003年(平成15年)問1 過去問解説
- 2003年(平成15年)問15
- 2003年(平成15年)問15 過去問解説
- 2005年(平成17年)問1
- 2005年(平成17年)問1 過去問解説
- 2005年(平成17年)問2
- 2005年(平成17年)問2 過去問解説
- 2007年(平成19年)問1
- 2007年(平成19年)問1 過去問解説
- 2007年(平成19年)問2
- 2007年(平成19年)問2 過去問解説
- 2008年(平成20年)問2
- 2008年(平成20年)問2 過去問解説
- 2009年(平成21年)問2
- 2009年(平成21年)問2 過去問解説
- 2010年(平成22年)問1
- 2010年(平成22年)問1 過去問解説
- 2011年(平成23年)問16
- 2011年(平成23年)問16 過去問解説
- 2012年(平成24年)問2
- 2012年(平成24年)問2 過去問解説
- 2013年(平成25年)問1
- 2013年(平成25年)問1 過去問解説
- 2014年(平成26年)問1
- 2014年(平成26年)問1 過去問解説
- 2014年(平成26年)問2
- 2014年(平成26年)問2 過去問解説
- 2016年(平成28年)問1
- 2016年(平成28年)問1 過去問解説
直流電動機のトルクと出力
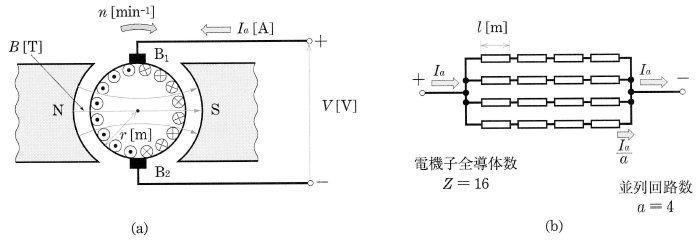
図に示すように、磁界中の電機子巻線に電流が流れると、各電機子巻線には電磁力が生じます。図において、電機子の半径を $r$[m]、磁極と電機子の間のエアギャップにおける平均磁束密度を $B$[T]、電機子巻線1本の長さを $l$[m]、並列回路数を $a$、電機子電流を $I_a$[A]とすると、導体1本に働く力 $F’$[N]およびトルク $T’$[N・m]は、それぞれ次式で表すことができます。
$F’=Bl×\displaystyle\frac{I_a}{a}$
$T’=F’r=\displaystyle\frac{BrlI_a}{a}$ … (1)
1極当たりの磁束を $ϕ$[Wb]、極数を $p$ とすると、エアギャップの平均磁束密度 $B$[T]は、次の式で表すことができます。
$B=\displaystyle\frac{ϕ}{A}=\displaystyle\frac{ϕ}{\displaystyle\frac{2πrl}{p}}=\displaystyle\frac{pϕ}{2πrl}$ … (2)
電機子の全導体数を $Z$[本]とすれば、電機子を回転させるトルク $T$[N・m]は、導体1本に働くトルク $T’$[N・m]のZ倍ですので、(1)式と(2)式より
$\begin{eqnarray}T&=&T’×Z=\displaystyle\frac{pϕ}{2πrl}×\displaystyle\frac{rlI_a}{a}×Z\\\\&=&\displaystyle\frac{pZ}{2πa}×ϕI_a=K_2ϕI_a… (4)\end{eqnarray}$
ただし、$K_2=\displaystyle\frac{pZ}{2πa}$ はトルク定数
トルク定数 $K_2$ は、電機子の構造から決まる定数です。直流電動機のトルクは、1極当たりの磁束 $ϕ$[Wb]と電機子電流 $I_a$[A]との積に比例することがわかります。
また,電機子全体には $F$[N]の力が働いているので、電機子が1回転する間にする仕事 $W$[J]は、次の式で表すことができます。
$W=2πrF=2πT$
直流電動機の回転速度を $n$[min-1]とすると、電機子が1秒間にする仕事、つまり出力 $P_o$[W]は、次の式で表すことができます。
$P_o=2π\displaystyle\frac{n}{60}T$ … (3)
このように、出力 $P_o$[W]は回転速度 $n$[min-1]とトルク $T$[N・m]の積に比例します。ここで、角周波数 $ω$[rsd/s]は、
$ω=\displaystyle\frac{2πn}{60}$[rsd/s] … (4)
ですので、(3)式は(4)式より、次のように表すことができます。
$P_o=2π\displaystyle\frac{n}{60}T=ωT$[W]
直流電動機のトルクを求める式①
$T=\displaystyle\frac{pZ}{2πa}ϕI_a$
$T$[N・m]:回転子に発生するトルク
$Z$:全導体数 (全コイル数)
$a$:並列回路数
$p$:磁極数
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$I_a$[A]:電機子電流
並列回路数 $a$ は、重ね巻では $a=p$、波巻では $a=2$ となります。
直流電動機のトルクを求める式②
$T=K_2ϕI_a$[N・m]
$T$[N・m]:回転子に発生するトルク
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$I_a$[A]:電機子電流
$K_2=\displaystyle\frac{pZ}{2πa}$ :トルク定数(比例定数)
回転速度 $n$ で回転する回転子が、1 秒間に回転する角度を求める式
$ω=\displaystyle\frac{2πn}{60}$
$ω$[rsd/s]:角速度
$n$[min-1]:回転速度
角速度 $ω$、トルク $T$ のときの出力を求める式
$P_o=ωT$
$P_o$[W]:直流電動機の機械的出力
$ω$[rsd/s]:角速度
$T$[N・m]:回転子に発生するトルク
逆起電力と回転速度
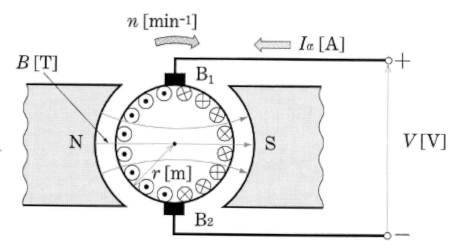
図において、外部から直流電圧 $V$[V]を加えると、電機子電流 $I_a$[A]が流れ、電機子が回転します。この場合、電機子巻線は磁束を切って回転しますので、フレミングの右手の法則により電機子巻線には、外部からの直流電圧と逆向きに、つまり電機子電流を減少させる向きに誘導起電力が生じます。この逆向きの誘導起電力を「逆起電力」といいます。また、この場合、電機子電流により、「電機子反作用」が生じています。
したがって、ブラシ接触電圧降下や電機子反作用を無視すると、直流電動機の電機子の回路は、次の等価回路で表すことができます。
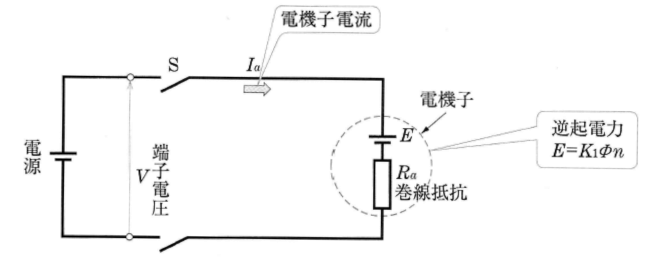
電機子電流 $I_a$[A]は、外部からの直流電圧、つまり電源の端子電圧 $V$[V]と逆起電力 $E$[V]の差の電圧に比例し、電機子巻線抵抗 $R_a$[Ω]に反比例し、次の式で表すことができます。
$I_a=\displaystyle\frac{V-E}{R_a}$ … (5)
電機子の回転速度を $n$[min-1]とすると、逆起電力 $E$[V]は、次の式で示すことが出来ます。
$E=\displaystyle\frac{Z}{a}pϕ\displaystyle\frac{n}{60}=K_1ϕn$ … (6)
ただし、$K_1=\displaystyle\frac{pZ}{60a}$ は電圧定数
(5)式を変形すると $E=V-R_aI_a$ となりますので、(6)式に代入して 、回転速度を $n$[min-1]について解くと、
$n=\displaystyle\frac{V-R_aI_a}{K_1ϕ}$ [min-1]
ただし、$K_1=\displaystyle\frac{pZ}{60a}$ は電圧定数
一般的に、電機子巻線抵抗 $R_a$[Ω]は、非常に小さい値ですので、$V>>R_aI_a$ となります。つまり、回転速度 $n$[min-1]は、端子電圧 $V$[V]に比例します。また、(5)式を変形すると $E=V-R_aI_a$ となりますので、両辺に $I_a$ を掛けると、
$EI_a=VI_a-R_a{I_a}^2$
となります。ここで、右辺の $VI_a$[W]は電機子の回路の入力、$R_aI_a^2$[W]は電機子巻線の回路の抵抗損ですので、$EI_a$[W]は、電動機において機械動力に変換される電力、つまり電動機の出力となります。したがって、電動機の出力 $P_o$[W]は、次の式で表すことができます。
$P_o=EI_a=VI_a-R_a{I_a}^2$
もし、直流電動機に課せられる機械的な負荷が増加し、回転速度 $n$[min-1]が低下すると、逆起電力 $E$[V]は、回転速度 $n$[min-1]に比例して減少します。また、端子電圧 $V$[V]が一定で逆起電力 $E$[V]が減少すると、電機子電流 $I_a$[A]は増加します。そうすると、直流電動機に供給される電力 $P_i$[W]は、$P_i=VI_a$ ですから、電動機の入力 $P_i$ が増えて電動機は回転し続けます。
直流電動機に発生する逆起電力を求める式
$E=e\displaystyle\frac{Z}{a}$
$E=\displaystyle\frac{pZ}{60a}ϕn$
$E=K_1ϕn$
$E$[V]:電機子巻線に発生する逆起電力
$e$[V]:1巻きのコイルに発生する誘導起電力
$Z$:全導体数 (全コイル数)
$a$:並列回路数
$p$:磁極数
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$n$[min-1]:電機子の回転速度
$K_1=\displaystyle\frac{pZ}{60a}$ :電圧定数(比例定数)
直流発電機の起電力を求める式と同じです。
直流電動機の端子電圧を求める式
$V=E+I_aR_a$
$V$[V]:端子電圧(電機子巻線に供給される電圧)
$E$[V]:逆電機子巻線に発生する逆起電力
$I_a$[A]:電機子電流
$R_a$[Ω]:電機子巻線抵抗
直流モーターの回転速度を求める式①
$n=\displaystyle\frac{E}{K_1ϕ}$
$n$[min-1]:電機子の回転速度
$E$[V]:電機子巻線に発生する逆起電力
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$K_1=\displaystyle\frac{pZ}{60a}$ :電圧定数(比例定数)
直流モーターに発生する逆起電力を求める式 $E=K_1ϕn$ を $n=$ の形にしたものです。
直流モーターの回転速度を求める式②
$n=\displaystyle\frac{V-I_aR_a}{K_1ϕ}$
$n$[min-1]:電機子の回転速度
$V$[V]:端子電圧(電機子巻線に供給される電圧)
$I_a$[A]:電機子電流
$R_a$[Ω]:電機子巻線抵抗
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$K_1=\displaystyle\frac{pZ}{60a}$ :電圧定数(比例定数)
直流モーターの回転速度を求める式① $n=\displaystyle\frac{E}{K_1ϕ}$ に 直流電動機の端子電圧を求める式 $V=E+I_aR_a$ を代入したものです。
直流電動機の出力を求める式②
$P_o=EI_a$
$P_o$[W]:直流電動機の機械的出力
$E$[V]:電機子巻線に発生する逆起電力
$I_a$[A]:電機子電流
角速度 $ω$、トルク $T$ のときの出力を求める式 $P_o=ωT$ とイコールで結ぶことができます。$P_o=ωT=EI_a$
電機子反作用と対策
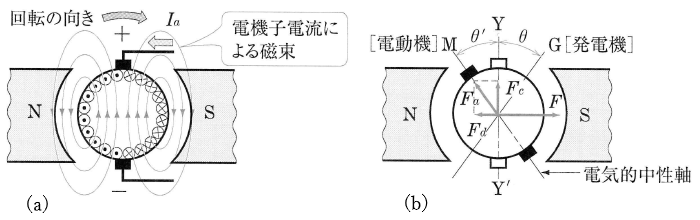
直流電動機の場合にも、電機子電流が流れることによって電機子反作用が生じます。このとき、電機子電流の向きは、直流発電機の場合と逆向きであるため、電機子電流 $I_a$[A]による磁界が、図の(a)に示す向きに生じます。この磁界の磁束と界磁磁束が合成された電気的中性軸は、回転の向きと逆向きに角 θ′[rad]だけかたよります。そこで電動機の場合も、起磁力をベクトルで表すと、図の(b)に示すようになります。そのため、整流子とブラシの間に火花などが発生しないようにするために、発電機の場合と逆向きにブラシを移動させなければなりません。
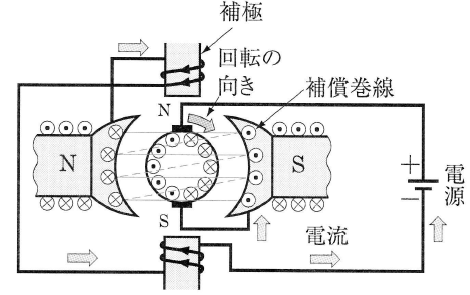
しかし、図(c)に示す補償巻線や補極を設けることによって、電機子反作用を防止することができます。この場合、電機子反作用や整流作用の向きが直流発電機の場合とは反対になりますので、補償巻線や補極の極性は、直流発電機の場合と反対でなければなりませんが、電機子電流の向きが反対であるので、それらの接続は直流発電機の場合と同じでよいことになります。
電機子反作用による影響
- 電気的中性軸が移動する
- 電気的中性軸が移動することにより、電機子巻線がブラシで短絡されブラシと整流子の間に火花が発生する
電機子反作用の対策
- 補償巻線を設ける
- 補極を設ける
直流電動機の種類と特徴
直流整流子電動機には、他励、分巻、直巻、複巻などの種類があり、それぞれの特徴により用途が分かれています。
他励電動機
直流他励電動機の等価回路図を示します。
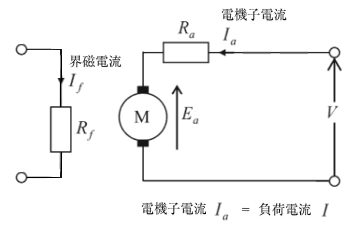
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]とすると、端子電圧 $V$[V]は次の式で表すことができます。
$V=E+R_aI_a$[V]
他励電動機の速度特性とトルク特性
直流他励電動機は、端子電圧(電源電圧)とは独立して界磁電流 $I_f$[A]を調整できるようになっています。界磁用の電源電圧を $V_f$[V]とすると、
$I_f=\displaystyle\frac{V_f}{R_f}$[A]
界磁磁束 $ϕ$[Wb]は、界磁電流 $I_f$[A]に比例します。また、一般的に電機子巻線抵抗 $R_a$[Ω]は、非常に小さい値ですので、$V>>R_aI_a$ となります。尚、他励電動機では、電機子電流 $I_a$[A]が、負荷電流 $I$[A]になります。
界磁用の電源電圧 $V_f$[V]と界磁抵抗 $R_f$[Ω]を一定として、回転速度 $n$ とトルク $T$ を見てみます。
回転速度:$n=\displaystyle\frac{V-R_aI}{K_1ϕ}$[min-1]
トルク:$T=\displaystyle\frac{pZ}{2πa}×ϕI_a=K_2ϕI$[N・m]
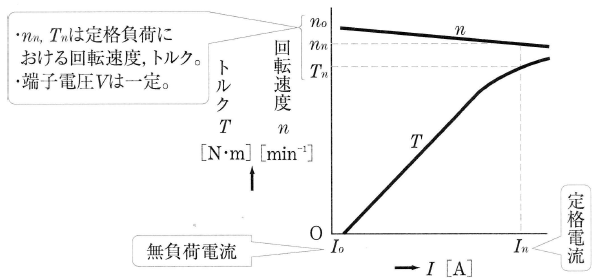
機械的な負荷が増加すると、負荷電流 $I$[A]が増加し、回転速度 $n$[min-1]の値はわずかに減少しますが、$R_aI$[V]は端子電圧 $V$[V]に比べてかなり小さいので、特性曲線に示すように、ほぼ一定となります。
他励電動機の界磁磁束は、ほぼ一定と考えてよいので、トルク $T$[N・m]は、負荷電流 $I$[A]にほぼ比例します。このように、負荷の変化に関係なく、回転速度が一定な電動機は、「定速度電動機」とよばれます。
他励電動機の主な用途としては、大型圧延機・クレーン・エレベーターなどに使われています。
他励電動機の各値
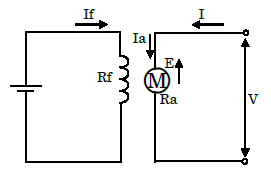
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力(逆起電力)
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$I_aR_a$:電機子抵抗による電圧降下
電流の関係式
$I=I_a$
他励電動機における各種公式
回転速度:$n=\displaystyle\frac{V-R_aI}{K_1ϕ}$[min-1]
トルク:$T=\displaystyle\frac{pZ}{2πa}×ϕI_a=K_2ϕI$[N・m]
分巻電動機
分巻電動機の等価回路図を示します。
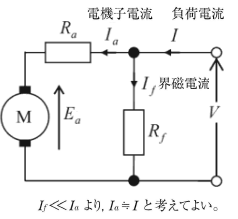
電機子電流を $I_a$[A]、電機子抵抗を $R_a$ [Ω] 、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]とすると、端子電圧を $V$[V]は次の式で表すことができます。
$V=E+R_aI_a$[V]
分巻電動機の速度特性とトルク特性
等価回路図において、端子電圧 $V$[V]、界磁抵抗 $R_f$[Ω]を一定にすれば、界磁磁束 $ϕ$[Wb]は一定です。また、界磁電流 $I_f$[A]は、電機子電流 $I_a$[A]に比べて非常に小さい値ですので、電機子電流 $I_a$≒負荷電流 $I$ となります。界磁用の電源電圧 $V_f$[V]と界磁抵抗 $R_f$[Ω]を一定として、回転速度 $n$ とトルク $T$ を見てみます。
回転速度:$n=\displaystyle\frac{V-R_aI_a}{K_1ϕ}$[min-1]
トルク:$T=\displaystyle\frac{pZ}{2πa}×ϕI_a=K_2ϕI_a$[N・m]

機械的な負荷が増加すると、負荷電流 $I$[A]が増加し、回転速度 $n$[min-1]の値はわずかに減少しますが、$R_aI$[V]は端子電圧 $V$[V]に比べてかなり小さいので、特性曲線に示すように、ほぼ一定となります。
分巻電動機の界磁磁束は、ほぼ一定と考えてよいので、トルク $T$[N・m]は、負荷電流 $I$[A]にほぼ比例します。
以上のように、分巻電動機の速度特性とトルク特性は、他励電動機と同じような曲線となります。尚、分巻電動機のトルクは $K_2ϕI$ で表されますが、実際に使用できる有効なトルク $T$[N・m]は、 $K_2ϕI$[N・m]から無負荷電流 $I_o$[A]によるトルク $K_2ϕI_o$[N・m]を減じたものです。つまり、実際に使用できる有効なトルク $T$[N・m]は、
$T=K_2ϕ(I-I_o)$[N・m]
で、表すことができます。
分巻電動機も他励電動機と同様に、負荷トルクが増加しても速度はほぼ一定になるため、「定速度電動機」といえます。分巻電動機の主な用途としては、圧延機・ポンプなどに使われています。
分巻電動機の各値
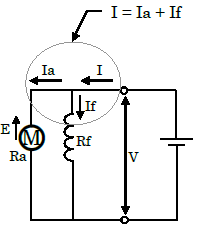
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力(逆起電力)
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$I_aR_a$:電機子抵抗による電圧降下
電流の関係式
$I=I_a+I_f$,$I_f=\displaystyle\frac{V}{R_f}$
分巻電動機における各種公式
回転速度:$n=\displaystyle\frac{V-R_aI_a}{K_1ϕ}$[min-1]
トルク:$T=\displaystyle\frac{pZ}{2πa}×ϕI_a=K_2ϕI_a$[N・m]
直巻電動機
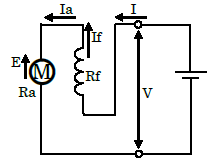
直巻電動機の等価回路図を示します。
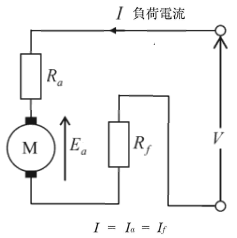
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]とすると、端子電圧 $V$[V]は次の式で表すことができます。
$V=E+(R_a+R_f)I$[V]
直巻電動機の速度特性とトルク特性
直巻電動機は、電機子コイルと界磁コイルが直列に結ばれています。これは、電機子電流 $I_a$[A]と界磁電流 $I_f$[A]が等しく、また負荷電流 $I$[A]も等しくなります。
$I_a=I_f=I$[A]
界磁磁束 $ϕ$[Wb]は界磁電流 $I_f$[A]によってつくられます。つまり、界磁磁束が磁気飽和しない場合は、界磁磁束 $ϕ$[Wb]は、負荷電流 $I$[A]に比例します。これらを考慮して、回転速度 $n$ とトルク $T$ を見てみます。
回転速度:$n=\displaystyle\frac{V-R_aI}{K_1ϕ}∝\displaystyle\frac{V-R_aI}{K_1I}$[min-1]
トルク:$T=K_2ϕI∝{K_2}I^2$[N・m]
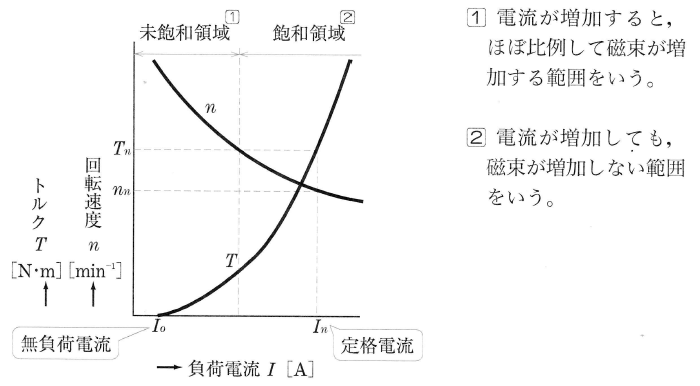
界磁磁束の未飽和領域では、回転速度 $n$[min-1]は、負荷電流 $I$[A]の増加に反比例して減少します。トルク $T$[N・m]は、負荷電流の2乗に比例します。飽和領域になると、回転速度 はほぼ一定に、トルクは、負荷電流にほぼ比例します。
このように、直巻電動機は、負荷電流の増減によって回転速度が大きく変わるので、「変速度電動機」とよばれます。直巻電動機は、無負荷に近づくと回転速度が異常に高速になるので、無負荷では絶対に運転してはいけません。
巻電動機の主な用途としては、電車・クレーン・巻上機などに使われています。
直巻電動機の各値
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力(逆起電力)
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$I_aR_a$:電機子抵抗による電圧降下
電流の関係式
$I_a=I_f=I$
直巻電動機における各種公式
回転速度:$n=\displaystyle\frac{V-R_aI}{K_1ϕ}∝\displaystyle\frac{V-R_aI}{K_1I}$[min-1]
トルク:$T=K_2ϕI∝{K_2}I^2$[N・m]
複巻電動機の特性
複巻電動機は、回路図に示すように、直巻界磁巻線と分巻界磁巻線が施され、合成界磁磁束が直巻界磁磁束と分巻界磁磁束の和になっている構造のものを「和動複巻電動機」といい、差になっている構造のものを「差動複巻電動機」といいます。
一般には、和動複巻電動機が用いられ、特性は、特性曲線に示すようになり、分巻の場合に比べると、負荷電流の増加に従って、回転速度 $n$[min-1]減少の割合が大きく、トルク $T$[N・m]は増加の割合が大きくなります。
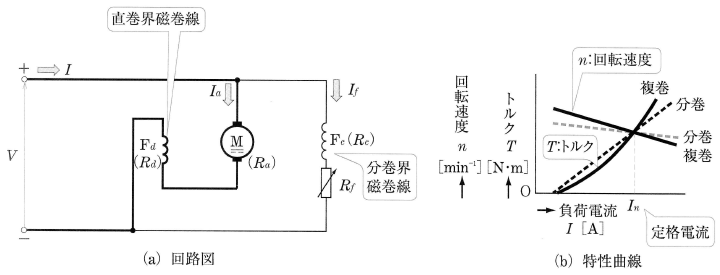
複巻電動機は、直巻界磁巻線と分巻界磁巻線の2つの界磁巻線を巻いていますので、直巻電動機と分巻電動機の中間の特性が得られます。特性曲線も、直巻電動機と分巻電動機の中間の形になります。
電験三種-機械の過去問解説:直流電動機の種類と特性
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問10
直流直巻電動機の負荷電流が 40[A]、負荷トルク 500[N・m]で全負荷運転している。負荷電流が 20[A]に減少したときの負荷トルク[N・m]の値として、正しいのは次のうちどれか。ただし、電機子電流が 40[A]以下の範囲では、この電動機の磁気回路の飽和は、無視してよいものとする。
(1) 100 (2) 125 (3) 250 (4) 354 (5) 1000
1997年(平成9年)問10 過去問解説
直巻電動機のトルク $T$[N・m]は、界磁磁束の未飽和領域を考えると、次の式で示されます。
$T=K_2ϕI={K_2}I^2$
全負荷のトルクを $T$[N・m]、軽負荷時のトルクを $T’$[N・m]とすると、
$500={K_2}×40^2$ … (1)
$T’={K_2}×20^2$ … (2)
(1),(2)式を解くと
$T’=500×\displaystyle\frac{20^2}{40^2}=125$[N・m]
答え (2)
1998年(平成10年)問12
直流分巻電動機が入力電圧 100[V]、入力電流 21[A]、回転速度 1200[r/min]で運転されている。この場合の発生トルク[N・m]の値として、正しいのは次のうちどれか。ただし、界磁回路の抵抗は 100[Ω]、電機子回路の抵抗は 0.2[Ω]とする。
(1) 1.5 (2) 1.6 (3) 15 (4) 17 (5) 19
1998年(平成10年)問12 過去問解説
発生トルク $T$、出力 $P$、角速度 $ω$ の関係は、
$T=\displaystyle\frac{P}{ω}$[N・m]
界磁電流を $I_f$[A] 、電機子電流を $I_a$[A]とすると、
$I_f=100V/100Ω=1$[A]
$I_a=21-1=20$[A]
電機子抵抗 $R_a=0.2$Ω なので、電機子電圧 $E_a$[V]、出力 $P$[W]は、
$E_a=100-0.2×20=96$[V]
$P=E_a×I_a=96×20=1920$[W]
角速度 $ω$ は 1200[min-1]より
$ω=2π×\displaystyle\frac{1200}{60}=40π$
したがって
$T=\displaystyle\frac{P}{ω}=\displaystyle\frac{1920}{40π}≒15$[N・m]
答え (3)
2001年(平成13年)問12
電機子回路の抵抗が 0.1[Ω]である直流分巻電動機が、電源電圧 110[V]、電機子電流 20[A]、回転速度 1,200[min-1]で運転されている。この電動機について、次の(a)及び(b)に答えよ。
(a) このときのトルク T[N・m]の値として、最も近いのは次のうちどれか。
(1) 0.29 (2) 1.8 (3) 17 (4) 54 (5) 110
(b) 界磁抵抗を調整して界磁磁束を 5[%]増加させたところ、電機子電流が 50[A]となった。このときの電動機の回転速度[min-1]の値として、最も近いのは次のうちどれか。
(1) 1060 (2) 1110 (3) 1170 (4) 1230 (5) 1260
2001年(平成13年)問12 過去問解説
(a) 発生トルク $T$、出力 $P$、角速度 $ω$ の関係は、
$T=\displaystyle\frac{P}{ω}$[N・m]
電機子電圧を $E_a$[A]、電機子電流を $I_a$[A]とすると、
$E_a=110-0.2×20=108$[V]
$P=E_a×I_a=108×20=2160$[W]
角速度 $ω$ は、1200rpmより
$ω=2π×\displaystyle\frac{1200}{60}=40π$
したがって
$T=\displaystyle\frac{P}{ω}=\displaystyle\frac{2160}{40π}≒17$[N・m]
答え (3)
(b) 端子電圧を $V$[V]、電機子電流を $I_a$[A] 、電機子抵抗を$R_a$[Ω]、磁束を $ϕ$[Wb]、電圧定数を $K_1$ とすると、回転速度 $n$[min-1]は、
$n=\displaystyle\frac{V-R_aI}{K_1ϕ}$
回転速度 1,200[min-1]のとき、
$1200=\displaystyle\frac{110-0.1×20}{K_1ϕ}$
$ K_1ϕ=\displaystyle\frac{108}{1200}=\displaystyle\frac{9}{100}$
界磁磁束を 5[%]増加させたとき、
$n=\displaystyle\frac{110-0.1×50}{\displaystyle\frac{9}{100}×1.05}=\displaystyle\frac{105×100}{9×1.05}≒1110$[min-1]
答え (2)
2003年(平成15年)問1
次の文章は、直流電動機のトルク特性に関する記述である。
- 分巻電動機のトルクは、負荷が小さい範囲では( ア )に比例して変化するが、その値がある程度以上になると、( イ )が増して磁束が減少するので、トルク曲線の傾きが穏やかになる。
- 直巻電動機のトルクは、界磁磁束の未飽和領域では界磁磁束が負荷電流に比例するので、負荷電流の( ウ )に比例して変化するが、負荷電流がある値以上になると磁気飽和のため界磁磁束はほぼ一定となるので、トルク曲線は負荷電流に比例して変化するようになる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 電機子電流 | 電機子反作用 | 2乗 |
| (2) | 電機子電流 | 機械的損失 | 2乗 |
| (3) | 電機子電圧 | 電機子反作用 | 1乗 |
| (4) | 電機子電圧 | 機械的損失 | 1乗 |
| (5) | 電機子電圧 | 電機子反作用 | 2乗 |
2003年(平成15年)問1 過去問解説
分巻電動機のトルク特性
$T=K_2ϕ(I_a-I_o)$[N・m]
直巻電動機のトルク特性
$T=K_2ϕI={K_2}’I^2$[N・m]
- 分巻電動機のトルクは、負荷が小さい範囲では( 電機子電流 )に比例して変化するが、その値がある程度以上になると、( 電機子反作用 )が増して磁束が減少するので、トルク曲線の傾きが穏やかになる。
- 直巻電動機のトルクは、界磁磁束の未飽和領域では界磁磁束が負荷電流に比例するので、負荷電流の( 2乗 )に比例して変化するが、負荷電流がある値以上になると磁気飽和のため界磁磁束はほぼ一定となるので、トルク曲線は負荷電流に比例して変化するようになる。
答え (1)
2003年(平成15年)問15
電機子巻線の抵抗 0.05[Ω]、分巻巻線の抵抗 10[Ω]の直流分巻発電機がある。この発電機について、次の(a)及び(b)に答えよ。
ただし、この発電機のブラシの全電圧降下は 2[V]とし、電機子反作用による電圧降下は無視できるものとする。
(a) この発電機を端子電圧 200[V]、出力電流 500[A]、回転速度 1,500[min-1]で運転しているとき、電機子誘導起電力[V]の値として、正しいのは次のうちどれか。
(1) 224 (2) 225 (3) 226 (4) 227 (5) 228
(b) この発電機を入力端子電圧 200[V]、入力電流 500[A]で電動機として運転した場合の回転速度[min-1]の値として、最も近いのは次のうちどれか。
(1) 1145 (2) 1158 (3) 1316 (4) 1327 (5) 1500
2003年(平成15年)問15 過去問解説
(a) 直流分巻発電機を図に示します。
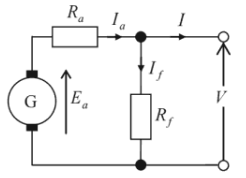
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とすると、
$I_f=\displaystyle\frac{V}{R_f}=\displaystyle\frac{200}{10}=20$[A]
$I_a=I+I_f=500+20=520$[A]
したがって、電機子誘導起電力を $E_a$[V]は、
$E_a=V+R_aI_a+2=200+0.05×520+2=228$[V]
答え (5)
(b) 直流分巻電動機を図に示します。
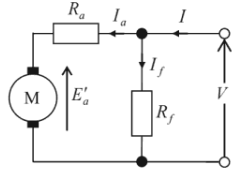
$I_f=\displaystyle\frac{V}{R_f}=\displaystyle\frac{200}{10}=20$[A]
$I_a=I-I_f=500-20=480$[A]
したがって、電機子誘導起電力を ${E_a}’$[V]は、
${E_a}’=V-R_aI_a-2=200-0.05×480-2=174$[V]
回転数は起電力に比例しますので、
$N=1500×\displaystyle\frac{{E_a}’}{E_a}=1500×\displaystyle\frac{174}{228}≒1145$[min-1]
答え (1)
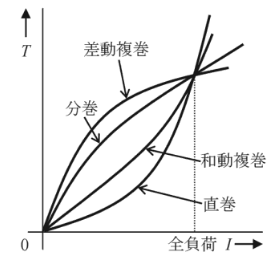
2005年(平成17年)問1
次の図は直流電動機の特性を示したものである。横軸を負荷電流 I[A]、 縦軸をトルク T[N・m]と回転速度 n[min-1]としたとき、特性を正しく表示している図は次のうちどれか。
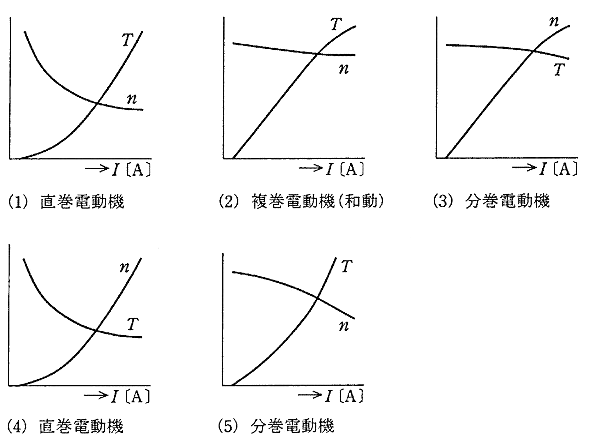
2005年(平成17年)問1 過去問解説
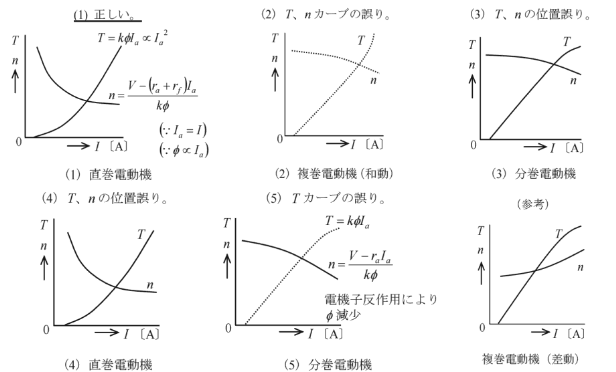
答え (1)
2005年(平成17年)問2
直流分巻電動機が電源電圧 100[V]、電機子電流 25[A]、回転速度 1,500[min-1]で運転されている。このときのトルク T[N・m]の値として、最も近いのは次のうちどれか。
ただし、電機子回路の抵抗は 0.2[Ω]とし、ブラシの電圧降下及び電機子反作用の影響は無視できるものとする。
(1) 0.252 (2) 15.1 (3) 15.9 (4) 16.7 (5) 95.0
2005年(平成17年)問2 過去問解説
発生トルク $T$、出力 $P$、角速度 $ω$ の関係は、
$T=\displaystyle\frac{P}{ω}$[N・m]
電機子電圧を $E_a$[A]、電機子電流を $I_a$[A]とすると、
$E_a=100-0.2×25=95$[V]
$P=E_a×I_a=95×25=2375$[W]
角速度 $ω$ は、1500[min-1]より
$ω=2π×\displaystyle\frac{1500}{60}=50π$
したがって、
$T=\displaystyle\frac{P}{ω}=\displaystyle\frac{2375}{50π}≒15.1$[N・m]
答え (2)
2007年(平成19年)問1
直流直巻電動機は、供給電圧が一定の場合、無負荷や非常に小さい負荷では使用することができない。この理由として、正しいのは次のうちどれか。
- 界磁電流と電機子電流がともに大きくなるので、界磁巻線や電機子巻線を焼損する危険性がある。
- 界磁電流が大きくなりトルクが非常に増大するので、駆動軸や電機子巻線を破損する危険性がある。
- 電機子電流が小さくなるので回転速度が減少し、回転が停止する。
- 界磁磁束が増大して回転速度が減少し、回転が停止する。
- 界磁磁束が小さくなって回転速度が非常に上昇するので、電機子巻線を破損する危険性がある。
2007年(平成19年)問1 過去問解説
直流直巻電動機の回路図を示します。

直巻電動機は、電機子コイルと界磁コイルが直列に結ばれています。これは、電機子電流 $I_a$[A]と界磁電流 $I_f$[A]が等しく、また負荷電流 $I$[A]も等しくなります。
界磁磁束 $ϕ$[Wb]は界磁電流 $I_f$[A]によってつくられます。つまり、界磁磁束が磁気飽和しない場合は、界磁磁束 $ϕ$[Wb]は、負荷電流 $I$[A]に比例します。回転速度は次の式で示すことができます。
$n=\displaystyle\frac{V-R_aI}{K_1ϕ}$[min-1]
$ϕ$ と$ I_a$ は、比例関係にありますので、無負荷や小さな負荷の場合は、回転速度が上がりすぎて危険です。
したがって、「界磁磁束が小さくなって回転速度が非常に上昇するので、電機子巻線を破損する危険性がある。」が正しい記述です。
答え (5)
2007年(平成19年)問2
直流分巻電動機があり、電機子回路の全抵抗(ブラシの接触抵抗を含む。)は、0.098[Ω]である。この電動機を端子電圧 220[V]の電源に接続して、ある負荷で運転すると、回転速度は 1480[min-1]、電機子電流は 120[A]であった。同一端子電圧でこの電動機を無負荷運転したときの回転速度[min-1]の値として、最も近いのは次のうちどれか。
ただし、無負荷運転では、電機子電流は非常に小さく、電機子回路の全抵抗による電圧降下は無視できるものとする。
(1) 1518 (2) 1532 (3) 1546 (4) 1559 (5) 1564
2007年(平成19年)問2 過去問解説
直流分巻電動機を図に示します。
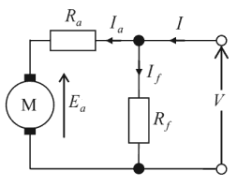
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とすると、
$E_a=V-R_aI_a=220-0.098×120=208.24$[V]
無負荷運転では、電機子電流は非常に小さくなりますので、電機子回路の電圧降下は無視できます。この時の、電機子誘導起電力を ${E_a}’$[V]は、
${E_a}’=V=220$[V]
回転数は起電力に比例しますので、
$n=1480×\displaystyle\frac{{E_a}’}{E_a}=1480×\displaystyle\frac{220}{208.24}≒1564$[min-1]
答え (5)
2008年(平成20年)問2
定格出力 5[kW]、定格電圧 220[V]の直流分巻電動機がある。この電動機を定格電圧で運転したとき、電機子電流が 23.6[A]で定格出力を得た。この電動機をある負荷に対して定格電圧で運転したとき、電機子電流が 20[A]になった。このときの逆起電力(誘導起電力)[V]の値として、最も近いのは次のうちどれか。
ただし、電機子反作用はなく、ブラシの抵抗は無視できるものとする。
(1) 201 (2) 206 (3) 213 (4) 218 (5) 227
2008年(平成20年)問2 過去問解説
直流分巻電動機を図に示します。

電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とすると、定格出力 $P_n$[W]は、
$P_n=E_aI_a$[W]
電動機を定格電圧で運転したとき、電機子電流が 23.6[A]で定格出力を得たので、
$5000=E_a×23.6$
$E_a≒211.9$[V]
したがって、電機子抵抗を $R_a$[Ω]は、
$V=E_a+R_aI_a$
$220=211.9+R_a×23.6$
$R_a≒0.343$[Ω]
電機子電流が 20[A]のときの逆起電力(誘導起電力)を ${E_a}’$[V]とすると、
${E_a}’=V-R_aI_a=220-0.343×20≒213$[V]
答え (3)
2009年(平成21年)問2
電機子回路の抵抗が 0.20[Ω]の直流他励電動機がある。励磁電流、電機子電流とも一定になるように制御されており、電機子電流は 50[A]である。回転速度が 1200[min-1]のとき、電機子回路への入力電圧は 110[V]であった。励磁電流、電機子電流を一定に保ったまま電動機の負荷を変化させたところ、入力電圧が 80[V]となった。このときの回転速度[min-1]の値として、最も近いのは次のうちどれか。
ただし、電機子反作用はなく、ブラシの抵抗は無視できるものとする。
(1) 764 (2) 840 (3) 873 (4) 900 (5) 960
2009年(平成21年)問2 過去問解説
直流他励電動機を図に示します。
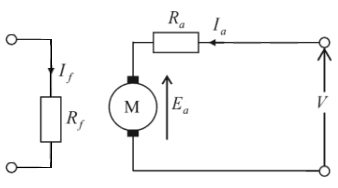
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とします。
入力電圧 110[V] 、電機子電流を 50[A]のときの、電機子誘導起電力を $E_a$[V]は、
$E_a=V-R_aI_a=110-0.2×50=100$[V]
入力電圧 80[V]、電機子電流を 50[A]のときの、電機子誘導起電力を ${E_a}’$[V]は、
${E_a}’=V-R_aI_a=80-0.2×50=70$[V]
回転数は起電力に比例しますので、
$n=1200×\displaystyle\frac{{E_a}’}{E_a}=1200×\displaystyle\frac{70}{100}=840$[min-1]
答え (2)
2010年(平成22年)問1
直流電動機の速度とトルクを次のように制御することを考える。
損失と電機子反作用を無視した場合、直流電動機では電機子巻線に発生する起電力は、界磁磁束と電機子巻線との相対速度に比例するので、( ア )では、界磁電流一定、すなわち磁束一定条件下で電機子電圧を増減し、電機子電圧に回転速度が( イ )するように回転速度を制御する。この電動機では界磁磁束一定条件下で電機子電流を増減し、電機子電流とトルクとが( ウ )するようにトルクを制御する。 この電動機の高速運転では電機子電圧一定の条件下で界磁電流を増減し、界磁磁束に回転速度が( エ )するように回転速度を制御する。 このように広い速度範囲で速度とトルクを制御できるので、( ア )は圧延機の駆動などに広く使われてきた。
上記の記述中の空自箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 直巻電動機 | 反比例 | 比例 | 比例 |
| (2) | 直巻電動機 | 比例 | 比例 | 反比例 |
| (3) | 他励電動機 | 反比例 | 反比例 | 比例 |
| (4) | 他励電動機 | 比例 | 比例 | 反比例 |
| (5) | 他励電動機 | 比例 | 反比例 | 比例 |
2010年(平成22年)問1 過去問解説
直流電動機の自励直巻と他励のうち、負荷電流に関係なく、界磁電流を一定にすることが出来るのは、他励電動機です。したがって(ア)は他励になります。直流他励電動機を図に示します。

電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とします。1極当たりの磁束を $ϕ$[Wb]、極数を $p$ 、並列回路数を $a$、電機子の全導体数を $Z$[本]、回転数を $n$、トルクを $T$[N・m]とすると、
$E_a=\displaystyle\frac{Z}{a}pϕ\displaystyle\frac{n}{60}=K_2ϕn$
$n=\displaystyle\frac{V-R_aI_a}{K_1ϕ}=\displaystyle\frac{E_a$}{K_2ϕ}$
$T=K_2ϕI_a$[N・m]
したがって、
(イ) 電気子電圧 $E_a$ と回転速度 $n$ は比例します。
(ウ) 電機子電流 $I_a$ とトルク $T$ は比例します。
(エ) 界磁電流 $I_f$[A]と磁束を $ϕ$[Wb]は比例するので、界磁電流 $I_f$[A]と回転速度 $n$ は反比例します。
答え (4)
2011年(平成23年)問16
負荷に直結された他励直流電動機を、電機子電圧を変化させることによって速度制御することを考える。
電機子抵抗が 0.4[Ω]、界磁磁束は界磁電流に比例するものとして、次の(a)及び(b)の問に答えよ。
(a) 界磁電流を $I_{f1}$[A]とし、電動機が 600[min-1]で回転しているときの誘導起電力は 200[V]であった。このとき電機子電流が 20[A]一定で負荷と釣り合った状態にするには, 電機子電圧を何[V]に制御しなければならないか、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 8 (2) 80 (3) 192 (4) 200 (5) 208
(b) 負荷は、トルクが一定で回転速度に対して機械出力が比例して上昇する特性であるとして、磁気飽和、電機子反作用、機械系の損失などは無視できるものとする。
電動機の回転速度を 1320[min-1]にしたときに,界磁電流を $I_{f1}$[A]の 1/2にして、電機子電流がある一定の値で負荷と釣り合った状態にするには、電機子電圧を何[V]に制御しなければならないか、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 216 (2) 228 (3) 236 (4) 448 (5) 456
2011年(平成23年)問16 過去問解説
(a) 直流他励電動機を図に示します。

電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とします。
$V=E+R_aI_a=200+0.4×20=208$[V]
答え (5)
(b) 1極当たりの磁束を $ϕ$[Wb]、極数を $p$ 、並列回路数を $a$、電機子の全導体数を $Z$[本]、回転数を $n$、トルクを $T$[N・m]とすると、
$E_a=\displaystyle\frac{Z}{a}pϕ\displaystyle\frac{n}{60}=K_2ϕn$
界磁電流を $I_f$[A]と磁束を $ϕ$[Wb]は、比例しますので、600[min-1]で回転しているときは、
$200=K_2ϕ×600$… (1)
1320[min-1]回転にしたときの、機子誘導起電力を ${E_a}’$[V]とすると、
${E_a}’=K_2ϕ×0.5×1320=K_2ϕ×660$… (2)
(1),(2)を解くと、
${E_a}’=220$[V]
トルクは、$T=K_2ϕI_a$[N・m]より、一定のトルク下では、磁束 $ϕ$[Wb]が 1/2になると、電機子電流 $I_a$[A]は2倍になりますので、
$V’={E_a}’+R_aI_a×2=220+0.4×20×2=236$[V]
答え (3)
2012年(平成24年)問2
直流他励電動機の電機子回路に直列抵抗 0.8[Ω]を接続して電圧 120[V]の直流電源で始動したところ、始動直後の電機子電流は 120[A]であった。電機子電流が 40[A]になったところで直列抵抗を 0.3[Ω]に切り換えた。インダクタンスが無視でき、電流が瞬時に変化するものとして、切換え直後の電機子電流[A]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、切換え時に電動機の回転速度は変化しないものとする。また、ブラシによる電圧降下及び電機子反作用はないものとし、電源電圧及び界磁電流は一定とする。
(1) 60 (2) 80 (3) 107 (4) 133 (5) 240
2012年(平成24年)問2 過去問解説
直流他励電動機を図に示します。

電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とします。
電機子抵抗を $R_a$[Ω]に、直列抵抗 0.8[Ω]を接続して電圧 120[V]の直流電源で始動したところ、始動直後の電機子電流は 120[A]であったので、
$V=(R_a+0.8)I_a $
$120=(R_a+0.8)×120 $
$R_a=0.2$[Ω]
電機子電流が 40[A]になったときの、電機子誘導起電力を ${E_a}’$[V]は、
${E_a}’=V-(R_a+0.8){I_a}’$
${E_a}’=120-(0.2+0.8)×40=80$[V]
直列抵抗を 0.3[Ω]に切り換えたときの、電機子電流 ${I_a}”$[A]は、
${E_a}’=V-(R_a+0.3){I_a}”$
$80=120-(0.2+0.3){I_a}”$
${I_a}”=80$[A]
答え (2)
2013年(平成25年)問1
直流電動機に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 分巻電動機は、端子電圧を一定として機械的な負荷を増加したとき、電機子電流が増加し、回転速度は、わずかに減少するがほぼ一定である。このため、定速度電動機と呼ばれる。
- 分巻電動機の速度制御の方法の一つとして界磁制御法がある。これは、界磁巻線に直列に接続した界磁抵抗器によって界磁電流を調整して界磁磁束の大きさを変え、速度を制御する方法である。
- 直巻電動機は、界磁電流が負荷電流(電動機に流れる電流)と同じである。このため、未飽和領域では界磁磁束が負荷電流に比例し、トルクも負荷電流に比例する。
- (直巻電動機は、負荷電流の増減によって回転速度が大きく変わる。トルクは、回転速度が小さいときに大きくなるので、始動時のトルクが大きいという特徴があり、クレーン、巻上機などの電動機として適している。
- 複巻電動機には、直巻界磁巻線及び分巻界磁巻線が施され、合成界磁磁束が直巻界磁磁束と分巻界磁磁束との和になっている構造の和動複巻電動機と、差になっている構造の差動複巻電動機とがある。
2013年(平成25年)問1 過去問解説
分巻電動機、直巻電動機、複巻電動機の回路図を示します。
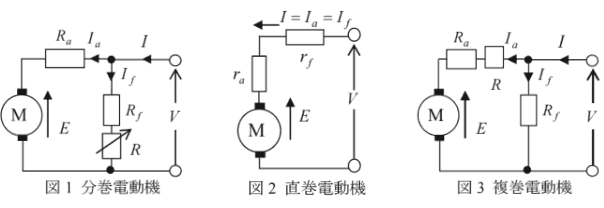
- 図1より、端子電圧 $V$ を一定として機械的な負荷を増加したときは、電機子誘導起電力を $E$[V]が減少し、電機子電流 $I_a$[A]は、増加しますが、電機子抵抗 $R_a$[Ω]は、小さいので、回転速度は、わずかに減少しますがほぼ一定となります。
$n=\displaystyle\frac{V-R_aI_a}{K_1ϕ}≒\displaystyle\frac{V}{K_1ϕ}$ - 図1の界磁抵抗器 $R$ の大きさを変えて、速度を制御する方法が界磁制御法です。
- 図2の直巻きのトルクは、$T=K_2ϕI_a$ で、未飽和領域では $T={K_2}’I^2$ となり、トルクは負荷電流の2乗に比例します。
- 回転速度は、 $n=\displaystyle\frac{V-R_aI}{K_1ϕ}=\displaystyle\frac{V-R_aI}{K_1I}$ で、大きく変わります。
- 図3のような複巻電動機には、直巻界磁巻線と分巻界磁巻線が施され、合成界磁磁束が直巻界磁磁束と分巻界磁磁束の和になっている構造のものを和動複巻電動機といい、差になっている構造のものを差動複巻電動機といいます。
したがって(3)の記述が誤りです。
答え (3)
2014年(平成26年)問1
次の文章は、直流電動機に関する記述である。
直流分巻電動機は界磁回路と電機子回路とが並列に接続されており、端子電圧及び界磁抵抗を一定にすれば、界磁磁束は一定である。このとき、機械的な負荷が( ア )すると、電機子電流が( イ )し回転速度はわずかに( ウ )するが、ほぼ一定である。このように負荷の変化に関係なく、回転速度がほぼ一定な電動機は定速度電動機と呼ばれる。
上記のように直流分巻電動機の界磁磁束を一定にして運転した場合、電機子反作用等を無視すると、トルクは電機子電流にほぼ( エ )する。
一方、直流直巻電動機は界磁回路と電機子回路とが直列に接続されており、界磁磁束は負荷電流によって作られる。界磁磁束が磁気飽和しない領域では、界磁磁束は負荷電流にほぼ( エ )し、トルクは負荷電流の( オ )にほぼ比例する。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 減少 | 減少 | 増加 | 反比例 | 1/2乗 |
| (2) | 増加 | 増加 | 増加 | 比例 | 2乗 |
| (3) | 減少 | 増加 | 減少 | 反比例 | 1/2乗 |
| (4) | 増加 | 増加 | 減少 | 比例 | 2乗 |
| (5) | 減少 | 減少 | 減少 | 比例 | 1/2乗 |
2014年(平成26年)問1 過去問解説
直流分巻電動機は界磁回路と電機子回路とが並列に接続されており、端子電圧及び界磁抵抗を一定にすれば、界磁磁束は一定である。このとき、機械的な負荷が( 増加 )すると、電機子電流が( 増加 )し回転速度はわずかに( 減少 )するが、ほぼ一定である。このように負荷の変化に関係なく、回転速度がほぼ一定な電動機は定速度電動機と呼ばれる。
上記のように直流分巻電動機の界磁磁束を一定にして運転した場合、電機子反作用等を無視すると、トルクは電機子電流にほぼ( 比例 )する。
一方、直流直巻電動機は界磁回路と電機子回路とが直列に接続されており、界磁磁束は負荷電流によって作られる。界磁磁束が磁気飽和しない領域では、界磁磁束は負荷電流にほぼ( 比例 )し、トルクは負荷電流の( 2乗 )にほぼ比例する。
答え (4)
2014年(平成26年)問2
出力 20kW、端子電圧 100V、回転速度 1500min-1で運転していた直流他励発電機があり、その電機子回路の抵抗は0.05Ωであった。この発電機を電圧 100Vの直流電源に接続して、そのまま直流他励電動機として使用したとき、ある負荷で回転速度は 1200min-1となり安定した。
このときの運転状態における電動機の負荷電流(電機子電流)の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、発電機での運転と電動機での運転とで、界磁電圧は変わらないものとし、ブラシの接触による電圧降下及び電機子反作用は無視できるものとする。
(1) 180 (2) 200 (3) 220 (4) 240 (5) 260
2014年(平成26年)問2 過去問解説
直流他励発電機を図に示します。
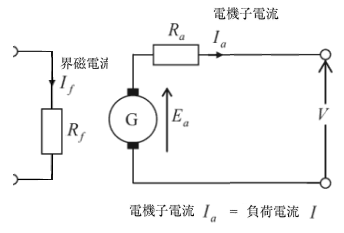
電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]、出力を $P$[W]とすると、
$I_a=\displaystyle\frac{P}{V}=\displaystyle\frac{20×10^3}{100}=200$[A]
$E_a=V+R_aI_a=100+200×0.05=110$[V]
発電機として運転しているときの、電機子誘導起電力を $E_a$[V]は、
$E_a=K_1ϕn$
$110=K_1ϕ×1500$ … (1)
電動機として運転しているときの、電機子誘導起電力を ${E_a}’$[V]とすると、
${E_a}’=K_1ϕn$
${E_a}’=K_1ϕ×1200$ … (2)
(1),(2)より、
${E_a}’=110×\displaystyle\frac{1200}{1500}=88$[V]
電動機の負荷電流(電機子電流)を ${I_a}’$[A]とすると、
${I_a}’=\displaystyle\frac{V-{E_a}’}{R_a}=\displaystyle\frac{100-88}{0.05}=240$[A]
答え (4)
2016年(平成28年)問1
電機子巻線抵抗が 0.2Ω である直流分巻電動機がある。この電動機では界磁抵抗器が界磁巻線に直列に接続されており界磁電流を調整することができる。また、この電動機には定トルク負荷が接続されており、その負荷が要求するトルクは定常状態においては回転速度によらない一定値となる。
この電動機を、負荷を接続した状態で端子電圧を 100V として運転したところ、回転速度は 1500min-1 であり、電機子電流は 50A であった。この状態から、端子電圧を 115V に変化させ、界磁電流を端子電圧が 100V のときと同じ値に調整したところ、回転速度が変化し最終的にある値で一定となった。この電動機の最終的な回転速度の値[min-1]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、電機子電流の最終的な値は端子電圧が 100V のときと同じである。また、電機子反作用及びブラシによる電圧降下は無視できるものとする。
(1) 1290 (2) 1700 (3) 1730 (4) 1750 (5) 1950
2016年(平成28年)問1 過去問解説
直流分巻電動機を図に示します。

電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]、負荷電流を $I$[A]、電機子誘導起電力を $E_a$[V]、端子電圧を $V$[V]とします。
端子電圧を 100V の時の誘導起電力を $E_{a}$[V]、115V の時の誘導起電力を ${E_a}’$[V]とすると、
$E_{a}=V-R_aI_a=100-50×0.2=90$[V]
${E_a}’=V’-R_aI_a=115-50×0.2=105$[V]
回転数は起電力に比例しますので、
$n=1500×\displaystyle\frac{{E_a}’}{E_a}=1500×\displaystyle\frac{105}{90}=1750$[min-1]
答え (4)
電験三種の機械科目に出題される「直流機」のページ
- 直流機の原理と構造
- 直流機の電機子反作用
- 直流発電機の種類と特性
- 直流電動機の種類と特性
- 直流電動機の始動と速度制御
- 直流機の定格






