電気の測定するときの目的には、非常に精度の高い測定を必要とすることもあれば、単に電圧が加わっているかどうかを確認すればよいといった場合もあります。どのような測定が必要かは、その目的を正しく理解し、その目的に適した方法のうちから、もっとも経済的な方法を選ばなければなりません。このページでは、初心者の方でもわかりやすいように、電気測定と誤差についてやさしく解説しています。
測定と誤差
三相交流の欠相検出のように、どの線に電圧が加わっているのかがわかればよい場合に、何百万円もする大形の電圧計を遠くから運んできて、長い時間をかけて測定する必要はなく、安価なテスタや相順計で十分です。しかし、高い精度を必要とする機器の出荷前検査では、その機器が保証している性能を有しているかどうかを確認する必要があります。
測定誤差は避けることができません。測定する前には、その目的を理解してどの程度の誤差が許されるのかを知った上で測定をする必要があります。
真の値と測定値
「測定量の正しい値」が真の値です。しかし、測定によって得られる値は真の値とは違ってきます。「測定によって求めた値」が測定値、「測定値から真の値を引いた値」が誤差です。
たとえば、電気回路の電流を測定する場合を想定してみます。電流は連続した値ですから、真の値は無限大の桁数をもった数値になってしまいます。長さを測定する場合も連続量ですから同様です。
「測定結果などを表す数字の内で、位取りを示すだけの0を除いた意味のある数字」を有効数字といいます。どのような計測器を使っても読み取りできる測定値の有効数字には限界がありますから、この点だけを考えても測定値と真の値は一致しません。
測定機器や方法を改善することによって、より真の値に近い測定値を得ることができるようになりますが、そのためには、高級な測定機器や測定法が要求されます。
JIS Z 8103計測用語の定義を引用しますと、正確さは「かたよりの小さい程度」、精密さは「ばらつきの小さい程度」、精度は「計測器が表す値または測定結果の正確さと精密さを含めた総合的な良さ」を意味しています。
実際の測定では、その目的から、 どのような精度が要求されているのか、いいかえれば、どの程度真の値に近い値を要求されているのかを考えて、どのような測定が要求を満たしていて、かつ、経済的であるかを決めていきます。
有効数字
次の表は、ある回路の電圧を測定したときにのデータシートを示します。
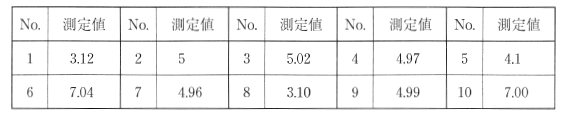
このデータシートは、№2と№5に誤りがあります。これ以外の測定値は小数点以下2桁まで数値が記入されているますが、№2の測定値は小数点以下の数値がありません。また、№5の測定値は小数点以下の1桁しか数値がありません。
№2は有効数字が1桁、№5は有効数字が2桁で、その他の値の3桁とは異なっています。№2の測定値がジヤスト5であれば5.00、№5も測定値がジヤスト4.1であれば、4.10と記載しなければなりません。5.00も5も同じように思うかも知れませんが、5という数値は、ジヤスト5を示しているのではなく、下の表のような 範囲を示していると考えることができます。

つまり、5、5.0、5.00は、それぞれ異なった意味合いをもっていることになります。たとえば、4.90という値は、5には含まれますが、5.0には含まれません。
ただし、値を表示するときに小数点以下の桁数を単に増やせばよいというものでもありません。測定値が、その数値が持つ範囲内に入っているという保証が必要です。± 5%の誤差がある可能性があるような測定では、± 0.1%の範囲を示す5.00という表し方は裏付けがないことになります。
誤差とばらつき
同じ条件で測定しても、測定にはある程度の不確かさがありますから、すべての測定値が一致するとは限りません。
真の値を知ることができませんので、誤差の正しい値も知ることはできません。誤差を一つの値ではなく範囲として考えればわかりやすいと思います。範囲とは、真の値は測定値に対して、この範囲内に入っていると考えられる数値です。
測定値は限りなく真の値に近づくことはできますが、真の値からはある量の開きをもっています。この開きは誤差と呼ばれています。
誤差は、絶対値あるいは誤差率で表されます。いま、測定値を$M$、真の値を$T$とすると、誤差量$ε$は、$ε=M-T$、誤差率(相対誤差)は$ε/T$で表されます。
一方で、測定値は測定のたびに異なります。これは「ばらつき」と呼ばれています。 この、ばらつきは統計処理により標準偏差で表すことができます。ばらつきの標準偏差は精密さの程度である精密度を表しており、ばらつきの母平均値に対する比は精密率と呼ばれます。
測定値から推定される母平均値から真の値を引くと、かたよりが求められます。かたよりの最大値は正確さの程度である正確度を表しており、その真の値に対する比は正確率と呼ばれます。精度とはこれらの精密さと正確さを総合したもので、誤差(かたよりとばらつきの両方を含んだ、真の値からの開き量)の母標準偏差に倍率を掛けた値の、 真の値に対する比で表されます。
標準偏差の倍率は明確に定められていません。いま、この値を3とすると、統計的に1000回の測定のうち約3回の測定値がこの範囲をはずれることを意味し、このように定めた精度は、ほとんどすべての指示値を含む範囲となります。
測定精度
精度とは、誤差の大きさを表す意味を持ちます。精度は「良い・悪い」で判定します。精度が良いというのは誤差が小さいことを意味し、精度が悪いというのは誤差が大きいということを意味しています。 測定値にはいろいろな原因で誤差が発生します。したがって、同じ条件の下で測定しても、測定値は必ずしも同じではなく、通常の場合、測定値の分布は正規分布になります。
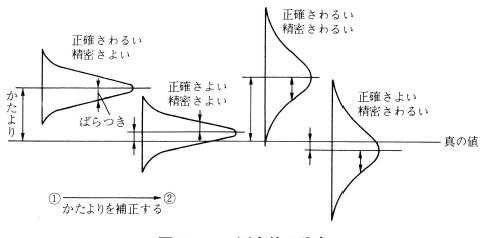
精密さというのは、ばらつきの程度を表す言葉で、精密さが良いというのは、ばらつきが小さい(測定値の分布の山がとがっている)ことを意味し、精密さが悪いというのは、ばらつきが大きい(山がなだらか)ことを意味しています。
また、測定器のゼロ点がずれていたり、アナログ計器(指針計器)で指針の読取り方向に誤ったくせがありますと、測定値が真の値に対してかたよりを生じることがあります。このかたよりの程度が正確さですから、正確さが良いとはかたよりが小さいことを、正確さが悪いとはかたよりが大きいことを意味しています。
誤差の分類
誤差はいろいろな原因によって発生しますが、誤差を原因別に分類すると次のようになります。
- 測定装置の誤差
- 測定環境による誤差
- 測定者による誤差
- 偶発的な誤差
測定装置の誤差
測定装置自体がもっている誤差です。これには、装置自体の精度から発生する誤差と測定方式による誤差とがあります。
装置自体の精度は、一般的なアナログ電圧計を例にとると、コイル、抵抗、磁石などの部品の精度や指針の支持部、バネの精度、日盛りの位置誤差などの影響を受けます。マイクロメータで長さを計測する場合を例に取ると、ねじのビッチ誤差、表面のあらさ、その他機械部品の精度や組立精度などの影響を受けます。
測定方式による誤差としては、連続量をディジタル計器で計測する場合は、ディジタル量として表示されている桁以下の値は読み取ることができません。アナログ方式では、目盛りの1/10まで読み取るのが一般的ですが、目盛りを100等分して読み取ることは事実上できません。したがって、それ以下の値は読み取れず、誤差の原因となります。これらの誤差は、測定者の注意によって誤差を軽減することができない性質のものです。
測定環境による誤差
測定環境については、計測器のマニュアルには、計測器の電源電圧、測定時や保管時の温度0湿度の条件などが示されています。正しい測定のためには機器の使用や保管が許容される環境条件の理解も重要なことです。
また、半導体素子のように温度により特性が大きく変化するものの測定では被測定物の温度についても注意を要します。半導体素子に比べて温度の影響が比較的少ない抵抗やコンデンサなどでも、正確な測定をする必要があるときには温度の影響を受けることを認識しておいてください。湿度の影響を受けやすいのは、高い抵抗値の測定です。湿度が高くなりますと絶縁物の抵抗が低下しますから、正しい抵抗値を測定ができているのか、抵抗を保持している絶縁物の抵抗なのか、湿度により低下している表面抵抗なのか、測定値はどれなのかが判らなくなってしまいます。
外部電界・磁界の影響を受けると電圧、電流などの測定に影響を受けます。磁界の強さを測定しているときは、地磁気や外部磁界の影響は誤差の原因になります。
測定者による誤差
測定者による誤差というのは、測定者の不注意、過失、思い込みや個人の読取り能力の限界などによって生じる誤差です。この誤差の例としては、読み違え、記録の間違い、測定方法の誤りなどがあり、測定者によって誤差の大きさが異なるのが特徴です。
この誤差は、測定者が測定機器、方法などを理解することや訓練することで、ある程度減らすことが可能ですが、完全になくすことはできません。
偶発的な誤差
偶発的な誤差とは、特定の原因ではなく、いろいろな要因によって偶発的に発生する誤差を意味しています。この誤差は、不規則に発生するもので、測定装置をより良いものに交換し、環境を改善し、測定者の教育訓練をしても避けることができません。
ただし、通常の測定ではこの誤差による影響はあまり大きくありませんから、他が原因の誤差を減らすことを考えるべきです。
誤差の補正
測定環境による誤差と測定者による誤差は、補正をすることで除去できる場合があります。補正量$α$は、$α=T-M$で求めることができます。補正率は$α/M$で表され、誤差率と同値となります。
偶発的な誤差は原因究明や補正処理できない確率的な現象ですので、統計法によって処理されます。
これらのように測定器が指示する値を標準器や基準と比較し、指示値との差を補正や統計処理して、測定器が真の値に近い値を示すようにすることを校正(calibration)といいます。また、校正法がより高位の標準によつて国家標準につながる経路が確立されている程度をトレーサビリティといいいます。



