このページでは、電気加熱の基礎について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された電気加熱の基礎の過去問題の解き方も解説しています。
電熱計算に用いられる単位
電熱計算に用いられる単位は、電気伝導に用いられる単位と相似性があります。
| 熱 系 | 電気系 |
|---|---|
| 温度：θ［℃］，t［K］ | 電位：E［V］ |
| 温度差：Δθ［℃］，Δt［K］ | 電位差：E［V］ |
| 熱量：Q［J］ | 電気量：Q［C］ |
| 熱流：I，Φ［W］ | 電流：I［A］ |
| 熱流密度：q［W/m2］ | 電流密度：J［A/m2］ |
| 熱伝導率：λ=1/ρ［W/m⋅K］ | 導電率：σ=1/ρ［S/m］ |
| 熱伝達率：α［W/m2⋅K］ | 表面抵抗率の逆数 |
| 熱抵抗：R［K/W］ | 電気抵抗：R［Ω］ |
| 熱容量：C［J/K］ | 静電容量：C［F］ |
熱量と熱容量
熱は高い温度から低い温度に移動する性質があります。例えば、水が入った鍋をコンロで加熱すると水の温度が上昇します。これはコンロの熱が鍋を通って移動したからです。このように、物体間で熱として移動するエネルギー量のことを熱量 Q といい、熱量の単位はジュール [J] が使われます。
例えば、10℃の水を50℃まで熱した場合を考えると、水という液体の状態は変らず温度だけが変わり、その温度変化は温度計で見ることができます。このように温度変化のみを行う熱量を顕熱といいます。
また、水を０℃に冷やした場合や、100℃まで熱した場合は、水から氷や水蒸気に状態が変化します。このような状態変化時に使われる熱を潜熱といいます。
質量 m［kg］、比熱 c［kJ/kg⋅K］の物体を t1［K］から t2［K］に上昇させるのに必要な熱量（エネルギー量） Q1 は、次の式で求めることができます。比熱とは、1kg の物質の温度を 1K（1℃）上げるのに必要な熱量(エネルギー量)のことで、水の比熱は 4.186［kJ/kg・K］です。
Q1=cm(t2-t1)=C(t2-t1)［kJ］
C［J/K］は、熱容量で物質の温度を 1K（1℃）上昇させるのに必要な熱量(エネルギー量)をいいます。
質量 m［kg］、潜熱β［kJ/kg］の物体を溶解，蒸発，凝固させるのに要する熱量 Q2 は、
Q2=βm［kJ］
熱エネルギーの伝わり方
熱は高い温度から低い温度へ伝わります。両者の温度が等しくなると、熱は移動（伝熱）しなくなります。このときを、熱平衡といいます。熱エネルギーの伝わり方（エネルギーの流れ）には、熱移動の3原則といわれる熱伝導，対流，熱放射の3種類があります。
熱移動の3原則の違いは、熱が何によって運ばれるかによる違いです。熱伝導は「物質」、対流は「流体や気体」、熱放射は「電磁波」が熱を運びます。
熱伝導（伝導）
熱伝導は、熱が物質よって運ばれる現象のことです。物体内部に温度差があると、高温部から低温部へと熱の流れが生じて、一方から他方に移動する現象です。
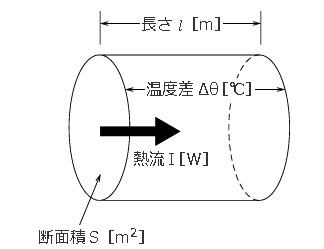
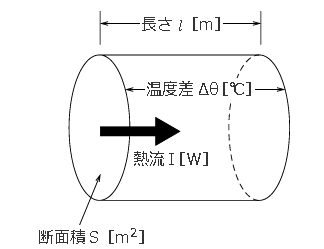
物体の熱伝導の能力を示す係数を熱伝導率 λ［W/m⋅K］といいます。この値が大きいほど熱を良く伝えます。図に示すような断面積 S［m2］、長さ $l$［m］の物体において両端面の温度差をΔθ［℃］、この物体内を熱が移動する場合の熱流を I［W］とすると、次の関係式が成り立ちます。
$I=λ\displaystyle\frac{S}{l}Δθ$［W］
上式は次のように変形できます。
熱回路のオームの法則
$Δθ=I\displaystyle\frac{l}{λS}=IR$［℃］
R［K/W］は、熱抵抗で物体の熱の伝わりにくさを表しています。
対流
対流は、液体や気体が温度差によって移動し、移動した液体や気体が熱を運ぶ現象です。液体や気体は、温度が上昇すると膨張し密度が小さくなり軽くなるため上昇します。そこへ、周囲の低温の密度が大きく重い部分が流れ込むことで循環が生じます。
物体から対流によって熱流が伝達されるときの伝達しやすさを示す係数を熱伝達率 α［W/m2⋅K］といいます。物体の表面積を S［m2］、周囲との温度差を Δt［K］としたとき、物体から対流によって伝達される熱流を I［W］とすると、次の関係式が成り立ちます。
$I=αS(t_2-t_1)=αSΔt=\displaystyle\frac{Δt}{R_S}$［W］
熱伝達率 $αS$ の逆数 $R_S=\displaystyle\frac{1}{αS}$［K/W］は表面熱抵抗と呼ばれています。
ふく射（放射）
一般に、熱せられた物体が放射熱を出して他の物体に熱を与えることをふく射（放射）という。太陽光やストーブ、焚き火などにあたると暖かく感じるのは熱放射によるものです。
入射するすべての放射を完全に吸収する仮想物体を黒体といいます。このような、黒体から単位面積当たりに発散されるエネルギー（放射発散度）はその絶対温度の4乗に比例します。この法則をステファン・ボルツマンの法則といいます。
放射発散度を Me［W/m2］ 、絶対温度をT［K］とすると、
Me=σT4
σはステファン・ボルツマン定数で、σ=5.670×10−8［W/m2⋅K4］
電験三種－機械（電熱）過去問
1997年（平成9年）問7
1気圧で 20［℃］の水 5.6［l］を一定の割合で加熱し、4時間ですべての水を蒸発させるには、何キロワットの電熱装置を必要とするか。正しい値を次のうちから選べ。ただし、水の蒸発熱を 540［kcal/kg］とし、また、電熱装置の効率を 70［%］とする。
(1) 0.19 (2) 1.2 (3) 1.4 (4) 1.8 (5) 2.1
1997年（平成9年）問7 過去問解説
20［℃］の水 5.6［l］を 100［℃］まで加熱するのに必要な熱量 Q1 は、水の比熱は、4.186［kJ/kg・K］ですので、
Q1＝4.186×5.6×(100-20)＝1875.3［kJ］
100［℃］の水 5.6［l］を全て蒸発させるのに必要な熱量 Q2 は、
Q2＝2260×5.6＝12656[kJ]
よって、20［℃］の水 5.6［l］を全て蒸発させるのに必要な熱量 Q は、
Q＝Q1＋Q2＝1875.3＋12656＝14531.3[kJ]
電熱装置の効率が 70［%］ですので、電熱装置に必要な入力電力 W1 は、
W1＝14531.3/0.7＝20759［kW］
4時間は、60×60×4＝14400［秒］ですので、必要な電熱装置のキロワット数 P は、
P＝20759/14400≒1.4［kW］
答え (3)
1998年（平成10年）問7
面積 25［m2］、厚さ 10［cm］、熱伝導率 0.4［W/(m・k)］の壁がある。この壁の内外面の温度差が 4［K］に保たれているとき、熱伝導によってこの壁を伝わる熱流［W］の値として、正しいのは次のうちどれか。
(1) 16 (2) 40 (3) 250 (4) 400 (5) 2500
1998年（平成10年）問7 過去問解説
面積を $S$［m2］、厚さを $l$［m］、熱伝導率を $λ$［W/m⋅K］、温度差を$Δθ$［℃］、熱流を $I$［W］とすると、
$I=λ\displaystyle\frac{S}{l}Δθ=0.4×\displaystyle\frac{25}{0.1}×4=400$［W］
答え (4)
1999年（平成11年）問7
電気炉の外壁に垂直に小穴をあけ、温度計を挿入して壁の外面から 10［cm］と 30［cm］の箇所で壁の内部温度を測定したところ、それぞれ 72［℃］と142［℃］の値が得られた。炉壁の熱伝導率を 0.94［W/(m・k)］とすれば、この炉壁からの単位面積当たりの熱損失［W/m2］の値として、正しいのは次のうちどれか。
(1) 3.29 (2) 14.9 (3) 165 (4) 329 (5) 1490
1999年（平成11年）問7 過去問解説
面積を $S$［m2］、厚さを $l$［m］、熱伝導率を $λ$［W/m⋅K］、温度差を$Δθ$［℃］、熱流を $I$［W］とすると、
$I=λ\displaystyle\frac{S}{l}Δθ$
単位面積当たりの熱損失［W/m2］は、$\displaystyle\frac{I}{S}$ ですので、
$\displaystyle\frac{I}{S}=λ\displaystyle\frac{1}{l}Δθ$
$=0.94×\displaystyle\frac{1}{0.3-0.1}×(142-72)$
$=329$［W/m2］
答え (4)
2003年（平成15年）問11
電気炉により、質量 500［kg］の鋳鋼を加熱し、時間 20［min］で完全に溶解させるのに必要な電力［kW］の値として、最も近いのは次のうちどれか。
ただし、鋳鋼の加熱前の温度は 15［℃］、溶解の潜熱は 314［kJ/kg］、比熱は 0.67［kJ/(kgK)］及び融点は 1,535［℃］であり、電気炉の効率は 80［%］とする。
(1) 444 (2) 530 (3) 555 (4) 694 (5) 2,900
2003年（平成15年）問11 過去問解説
融点まで加熱するのに必要な熱量 Q1 は
Q1=0.67×500×(1535－15)＝509200［kJ］
融点から溶けるまでに必要な熱量 Q2 は
Q2=314×500＝157000［kJ］
よって、15［℃］の鋳鋼 500［kg］を全て溶解させるのに必要な熱量 Q は、
Q＝Q1＋Q2＝509200＋157000＝666200[kJ]
電気炉の効率は 80［%］ですので、電気炉に必要な入力電力 W1 は、
W1＝666200/0.8＝832750［kW］
20［分]＝1200［秒]で、必要な電熱装置のキロワット数 P は、
P＝832750/1200≒694［kW］
答え (4)
2005年（平成17年）問17
20［℃］において含水量 70［kg］を含んだ木材 100［kg］がある。これを 100［℃］に設定した乾燥器によって含水量が 5［kg］となるまで乾燥したい。次の(a)及び(b)に答えよ。
ただし、木材の完全乾燥状態での比熱を 1.25［kJ/kg･K］、水の比熱と蒸発潜熱をそれぞれ 4.19［kJ/kg･K］，2.26×103[kJ/kg]とする。
(a) この乾燥に要する全熱量［kJ］の値として、最も近いのは次のうちどれか。
(1) 1.43×103 (2) 23.0×103 (3) 147×103 (4) 161×103 (5) 173×103
(b) 乾燥器の容量(消費電力)を 22［kW］、総合効率を 55［%］とするとき、乾燥に要する時間［h］の値として、最も近いのは次のうちどれか。
(1) 1.2 (2) 4.0 (3) 5.0 (4)14.0 (5) 17.0
2005年（平成17年）問17 過去問解説
(a) 20［℃］の木材 30［kg］を 100［℃］まで加熱するのに必要な熱量を Q1 、20［℃］の水 70［kg］を 100［℃］まで加熱するのに必要な熱量を Q1‘ とすると、
Q1=1.25×30×(100－20)＝3000［kJ］
Q1‘=4.19×70×(100－20)＝23469［kJ］
100［℃］の水 70［kg］を 5［kg］まで、蒸発させるのに必要な熱量 Q2 は、
Q2=2.26×103×(70-5)＝146900［kJ］
よって、乾燥に要する必要な熱量 Q は、
Q=Q1+Q2+Q3=3000+23469+146900≒173×103［kJ］
答え (5)
(b) 乾燥器の効率は 55［%］ですので、乾燥器に必要な入力電力 W1 は、
W1＝173×103/0.55≒314.5×103［kW］
消費電力 22［kW］の乾燥器を、1［h］運転したときの消費電力は、22×60×60=79.2×103［kW/h］ですので、乾燥に要する時間 T［h］は、
T=314.5×103/79.2×103≒4［h］
答え (2)
2006年（平成18年）問11
物体とその周辺の外気(気体又は液体)との間の熱の移動は、対流と( ア )によって行われる。そのうち、表面と周囲の温度差が比較的小さいときは対流が主となる。
いま、物体の表面積をS［m2］、周囲の温度差を t［K］とすると、物体から対流によって伝達される熱流 I［W］は次式となる。
I=αSt［W］
この式で、αは( イ )と呼ばれ、単位は［W/m2・K］で表される。この値は主として、物体の周囲の流体の流速によって大きくかわる。また、αの逆数1/αは( ウ )と呼ばれる。
上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 放射 | 熱伝達係数 | 表面熱抵抗率 |
| (2) | 伝導 | 熱伝達係数 | 表面熱抵抗率 |
| (3) | 伝導 | 熱伝導率 | 体積熱抵抗率 |
| (4) | 放射 | 熱伝達係数 | 体積熱抵抗率 |
| (5) | 放射 | 熱伝導率 | 表面熱抵抗率 |
2006年（平成18年）問11 過去問解説
物体とその周辺の外気(気体又は液体)との間の熱の移動は、対流と( 放射 )によって行われる。そのうち、表面と周囲の温度差が比較的小さいときは対流が主となる。
いま、物体の表面積をS［m2］、周囲の温度差を t［K］とすると、物体から対流によって伝達される熱流 I［W］は次式となる。
I=αSt［W］
この式で、αは( 熱伝達係数 )と呼ばれ、単位は［W/m2・K］で表される。この値は主として、物体の周囲の流体の流速によって大きくかわる。また、αの逆数1/αは( 表面熱抵抗率 )と呼ばれる。
答え (1)
2007年（平成19年）問12
電気的に温度を測定する方法には、熱電温度計、抵抗温度計など接触式のものと、放射温度計(全放射温度計、赤外線温度計)や光高温計など放射を利用した非接触式のものがある。
熱電温度計は、( ア )の熱起電力が熱接点と冷接点間の温度差に応じて生じるという（ イ ）効果を利用したものである。普通、温度差と熱起電力が直線的関係にある範囲で使用される。
抵抗温度計は、白金や銅，ニッケルなどの純粋な金属や（ ウ ）のような半導体の抵抗率が温度によって規則的に変化する特性を利用したものである。
全放射温度計は、「放射体から単位時間に放射される全放射エネルギーは放射体の絶対温度の（ エ ）に比例する」というステファン･ボルツマンの法則を応用したもので、光学系を使用して被測温体からの全放射エネルギーを受熱板に集めて、その温度上昇を熱電温度計などによって測定するものである。
赤外線温度計は，波長 700～20000［nm］程度の赤外放射を利用したもので、検出素子としては（ ウ ）などを使ったものと、HgCdTe，lnGaAs，PbSなどの（ オ ）を使ったものがある。
上記の記連中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 熱電対 | ゼーベック | サーミスタ | 4乗 | 光電素子 |
| (2) | サーミスタ | ペルチェ | バイメタル | 3乗 | 光電素子 |
| (3) | 熱電対 | ゼーベック | サーミスタ | 3乗 | 熱電素子 |
| (4) | 熱電対 | ペルチェ | バイメタル | 4乗 | 光電素子 |
| (5) | サーミスタ | ゼーベック | バイメタル | 4乗 | 熱電素子 |
2007年（平成19年）問12 過去問解説
電気的に温度を測定する方法には、熱電温度計、抵抗温度計など接触式のものと、放射温度計(全放射温度計、赤外線温度計)や光高温計など放射を利用した非接触式のものがある。
熱電温度計は、( 熱電対 )の熱起電力が熱接点と冷接点間の温度差に応じて生じるという（ ゼーベック ）効果を利用したものである。普通、温度差と熱起電力が直線的関係にある範囲で使用される。
抵抗温度計は、白金や銅，ニッケルなどの純粋な金属や（ サーミスタ ）のような半導体の抵抗率が温度によって規則的に変化する特性を利用したものである。
全放射温度計は、「放射体から単位時間に放射される全放射エネルギーは放射体の絶対温度の（ 4乗 ）に比例する」というステファン･ボルツマンの法則を応用したもので、光学系を使用して被測温体からの全放射エネルギーを受熱板に集めて、その温度上昇を熱電温度計などによって測定するものである。
赤外線温度計は，波長 700～20000［nm］程度の赤外放射を利用したもので、検出素子としては（ サーミスタ ）などを使ったものと、HgCdTe，lnGaAs，PbSなどの（ 光電素子 ）を使ったものがある。
答え (1)
2013年（平成25年）問17
伝熱に関する次の(a)及び(b)の問に答えよ。
(a) 直径 1［m］、高さ 0.5［m］の円柱がある。円柱の下面温度が 600［K］、上面温度が 330 ［K］ に保たれているとき、伝導によって円柱の高さ方向に流れる熱流[W]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、円柱の熱伝導率は 0.26［W/(m・K)］とする。また、円柱側面からの放射及び対流による熱損失はないものとする。
(1) 45 (2) 110 (3) 441 (4) 661 (5) 1630
(b) 次の文章は、放射伝熱に関する記述である。
すべての物体はその物体の温度に応じた強さのエネルギーを( ア )として放出している。その量は物体表面の温度と放射率とから求めることができる。
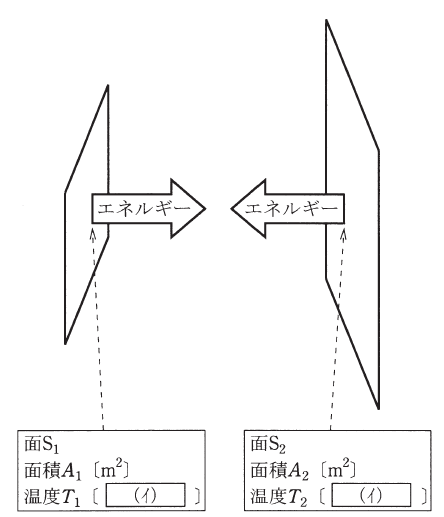
いま、図に示すように、面積 A1［m2］、温度 T1［( イ )］の面 S1と、面積 A2［m2］、温度 T2［( イ )］の面 S2とが向き合っている。両面の温度に T1＞T2 の関係があるとき、エネルギーは面 S1 から面 S2 に放射によって伝わる。そのエネルギー流量(1秒当たりに面 S1 から面 S2 に伝わるエネルギー)Φ［W］はΦ=εσA1F12×( ウ )で与えられる。
ここで、εは放射率、σは( エ )、及び F12 は形態係数である。ただし、εに波長依存性はなく、両面において等しいとする。また、F12 は面 S1、面 S2 の大きさ、形状、相対位置などの幾何学的な関係で決まる値である。
上記の記述中の空白箇所(ア)，(イ)，(ウ)，及び(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 電磁波 | K | (T1-T2) | プランク定数 |
| (2) | 熱 | K | (T14-T24) | ステファン・ボルツマン定数 |
| (3) | 電磁波 | K | (T14-T24) | ステファン・ボルツマン定数 |
| (4) | 熱 | ℃ | (T1-T2) | ステファン・ボルツマン定数 |
| (5) | 電磁波 | ℃ | (T14-T24) | プランク定数 |
2013年（平成25年）問17 過去問解説
(a) 面積を $S$［m2］、長さを $l$［m］、熱伝導率を $λ$［W/m⋅K］、温度差を$Δθ$［℃］、熱流を $I$［W］とすると、
$I=λ\displaystyle\frac{S}{l}Δθ$
$=0.26×\displaystyle\frac{0.25π}{0.5}×(600-330)$
$≒110$［W］
答え (2)
(b) すべての物体はその物体の温度に応じた強さのエネルギーを( 電磁波 )として放出している。その量は物体表面の温度と放射率とから求めることができる。
いま、図に示すように、面積 A1［m2］、温度 T1［( K )］の面 S1と、面積 A2［m2］、温度 T2［( K )］の面 S2とが向き合っている。両面の温度に T1＞T2 の関係があるとき、エネルギーは面 S1 から面 S2 に放射によって伝わる。そのエネルギー流量(1秒当たりに面 S1 から面 S2 に伝わるエネルギー)Φ［W］はΦ=εσA1F12×( (T14-T24) )で与えられる。
ここで、εは放射率、σは( ステファン・ボルツマン定数 )、及び F12 は形態係数である。ただし、εに波長依存性はなく、両面において等しいとする。また、F12 は面 S1、面 S2 の大きさ、形状、相対位置などの幾何学的な関係で決まる値である。
答え (3)
