第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「直流機の原理と構造」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「直流機の原理と構造」の過去問題も解説しています。
直流機の構造
直流機の構造は、「固定子(ステーター)」は界磁や継鉄などによって、「回転子(ローター)」には、電機子や整流子などによって構成されています。
- 固定子(ステーター):固定されている部品(界磁、継鉄など)
- 回転子(ローター):回転する部品(電機子、整流子など)
固定子
- 界磁
磁界を発生させる固定子または回転子のことを「界磁」といいます。界磁には永久磁石や電磁石が使用されます。直流機の場合は、固定子側が界磁になります。
- 継鉄
直流機の外枠を構成します。磁気回路としての役目もあります。
- 磁極片
界磁鉄心から出た磁束を、電機子表面に平等に分布させます。
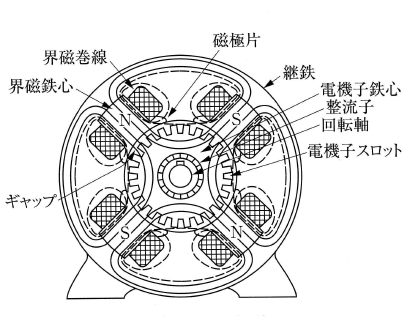
回転子
回転子は、「電機子・整流子・軸」で構成され、一体となっています。電機子は、常に一定方向だけの電流を流しても回転力が発生しないため、回転角度によって機械的に接点が入れ替わり、それによって電流の流れる方向も切り替わるようにします。そのために用意される固定側の端子をブラシ、回転側の端子を整流子と呼び、このような仕組みにより連続して回転することができます。
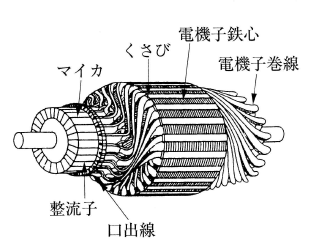
実際の直流機では磁束を通りやすくするため磁極間に円筒形の鉄心が置かれます。また、コイルは鉄心の表面にある「スロット(切り込み)」のなかに収納され、鉄心ごと回転するようになっています。鉄心とコイルを組み合わせた装置を「電機子」といい、円筒形の鉄心を「電機子鉄心」、コイルを「電機子巻線」といいます。
直流発電機の電機子巻線と誘導起電力
図3のように、磁極間に置いた方形コイルの両端を二つの銅片 $C_1 , C_2$ に接続します。コイルをXX′を軸として時計方向に回転させると、コイルには誘導起電力が発生します。
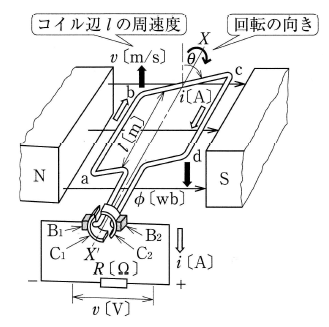
この誘導起電力 $e$[V]は、フレミングの右手の法則より、コイルの半回転ごとに向きが変わる図4(a)に示すような正弦波交流が発生します。
しかし、コイルの両端に「整流子」と呼ばれる半円形の銅片 $C_1 , C_2$ とこれに接触する「ブラシ」とよばれる端子 $B1 , B2$ の働きによって、コイルに生じた起電力は図4(b)に示すような脈動電圧になり、負荷には常に一定の向きの電流が得られます。
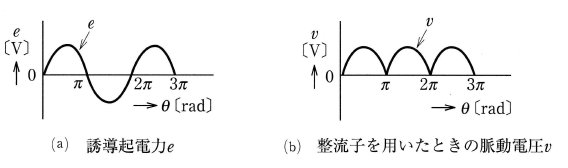
整流子はコイルと一緒に回転します。コイルが半回転して電流の向きが変わるとブラシに接触した整流子も入れ替わるため、ブラシには常に同じ方向の電流が流れるしくみになっています。ただし、コイルが2辺しかないと脈動の激しい電気になってしまいますので、実際の発電機ではコイル辺をたくさん設けて、より直流に近い電気をつくります。
この誘導起電力 $e$[V]は、磁束密度を $B$[T]、導体の長さを $l$[m]、コイル辺の周速度を $v$[m/s]とすると、次の式で表すことができます。
$e=Blv$[V]… (1)
また、コイル辺の周速度を $v$[m/s]は、コイルの直径を $D$[m]、コイルの回転速度を $n$[min-1]とすると、つぎの式で表すことができます。
$v=ωr=\displaystyle\frac{2πn}{60}×\displaystyle\frac{D}{2}=\displaystyle\frac{πDn}{60}$[m/s]… (2)
ただし、$ω$は角速度、$r$ は半径
平均磁束密度が $B$[T]は、合計磁束をそれに垂直な面積 $S$[m2]で割ったものですので、毎極の磁束を $ϕ$[Wb]、磁極数を $p$ とすると、
$B=\displaystyle\frac{pϕ}{S}=\displaystyle\frac{pϕ}{πDl}$[T]… (3)
(1)式に(2),(3)式を代入すると、
$e=Blv=\displaystyle\frac{pϕ}{πDl}×l×πD\displaystyle\frac{n}{60}=\displaystyle\frac{pϕn}{60}$[V]
ただし、コイルは一巻き
磁石のN極とS極を磁極といい、磁極数とは「磁極がいくつあるか」を表わしています。磁極数のことを極数ともいいます。また、N極とS極が対になったものを極対数といい、極数の1/2になります。
電機子巻線の巻線方法
電機子巻線の巻き方には重ね巻と波巻の2種類があります。巻線方式は、電動機ではトルクに、発電機の場合は誘導起電力に影響を与えます。両者の違いは隣どうしのコイルのつなぎ方です。
重ね巻
重ね巻はコイル辺を1本ずつずらしながらスロットに収めていく巻き方です。重ね巻は、電機子コイル一巻きで、隣の整流子片に接続します。極数と並列回路数が等しくなりますので、多極機では並列回路数が多くなります。誘導起電力に微妙な差があると、循環電流が流れて巻線を過熱します。これを防ぐために、等電位となるべきコイルを結線し、均圧環を設けます。
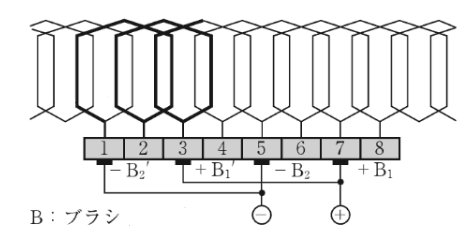
重ね巻の特徴
- 磁極と同数の回路を並列に接続
- 磁極と同数のブラシがある
- 並列回路が多くなる場合は、均圧環が必要
- 定電圧、大電流機に適する
波巻
波巻は1回路のコイル辺が全スロットに収まるように、波巻に巻いていく巻き方です。電機子コイル一往復で、整流子片に接続します。ブラシからみると、コイルが2つに枝分かれしているので、並列回路数は2になります。
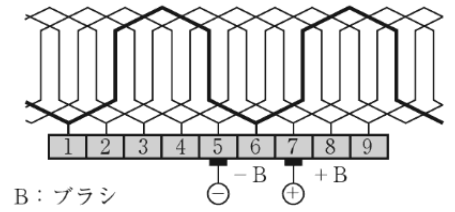
波巻の特徴
- 並列回路は磁極数にかかわらず2
- ブラシの数は磁極数にかかわらず2(正負の1対)
- 均圧環は不要
- 高電圧、小電流機に適する
電機子巻線の並列回路と誘導起電力
電機子巻線を延ばしてみるとコイル辺を直列につないだ回路が図のように並列に接続されていることがわかります。
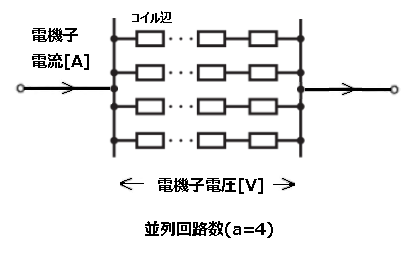
つまり、電機子全体の誘導起電力は次のように計算することができます。
電機子全体の誘導起電力=コイル1辺の誘導起電力×$\displaystyle\frac{コイル総数}{並列回路数}$[V]
コイル1辺の誘導起電力を $e$、電機子の導体数(コイル辺の総数)を $Z$、電機子の並列回路数を $a$ とすると、電機子全体の誘導起電力 $E$[V]は次の式になります。
$E=e×\displaystyle\frac{Z}{a}=\displaystyle\frac{pϕn}{60}×\displaystyle\frac{Z}{a}=\displaystyle\frac{pZ}{60a}ϕn=K_1ϕn$[V]
ただし、$K_1=\displaystyle\frac{pZ}{60a}$ は電圧定数
電圧定数 $K_1=\displaystyle\frac{pZ}{60a}$ は、発電機の構造から決まる定数で、直流発電機の起電力は1極当たりの磁束と回転速度の積に比例することを意味しています。
また、電機子電流は次のように計算することができます。
電機子電流=コイル電流×並列回路数[A]
並列回路の数は重ね巻の場合は磁極数と等しく波巻の場合は磁極数にかかわらず2本です。そのため一般に電機子全体の誘導起電力は波巻のほうが大きく、電機子電流は重ね巻の方が大きくなります。
直流発電機の起電力を求める公式①
$E=e\displaystyle\frac{Z}{a}$
$E$[V]:直流発電機に発生する誘導起電力
$e$[V]:1巻きの巻線(コイル)に発生する誘導起電力
$Z$:全導体数 (全コイル数)
$a$:並列回路数
全導体数 $Z$ とは、電機子に巻かれている巻線の数のことです。並列回路数 $a$ は、重ね巻では $a=p$、波巻では $a=2$ となります。($p$:磁極数)
直流発電機の起電力を求める公式②
$E=\displaystyle\frac{pZ}{60a}ϕn$
$E$[V]:直流発電機に発生する誘導起電力
$Z$:全導体数 (全コイル数)
$a$:並列回路数
$p$:磁極数
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$n$[min-1]:電機子の回転速度
並列回路数 $a$ は、重ね巻では $a=p$、波巻では $a=2$ となります。
直流発電機の起電力を求める公式③
$E=K_1ϕn$
$E$[V]:直流発電機に発生する誘導起電力
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$n$[min-1]:電機子の回転速度
$K_1=\displaystyle\frac{pZ}{60a}$ :電圧定数(比例定数)
直流電動機のトルクと機械的出力
直流発電機に外部から直流電圧を加えると、電機子に電流が流れ、電流と界磁磁束との間に電磁力が働き、電機子は回転します。このことは、直流発電機はそのまま直流電動機として用いることができることを示します。つまり、構造上は全く同じです。
図8のように、XX′を回転軸とする方形コイルを置くとします。このコイルに電流を流すと、各コイル辺(ab,cd)には、それぞれフレミングの左手の法則によって定まる向きに電磁力 $f$[N]が働きます。したがって、コイルは時計方向に回転します。
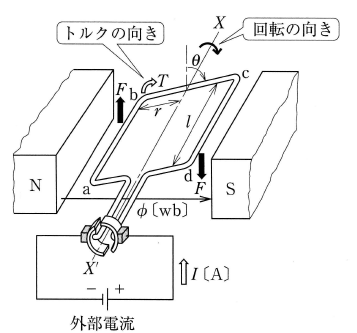
電磁力 $f$[N]は、磁束密度を $B$[T]、導体の長さを $l$[m]、コイル電流を $I$[A]とすると、つぎの式で表すことができます。
$f=BIl$[N]… (4)
(4)式に(3)式を代入すると、
$f=BIl=\displaystyle\frac{pϕ}{πDl}×I×l=\displaystyle\frac{pϕ}{πD}I$[N]… (5)
電機子の導体数(コイル辺の総数)を $Z$、電機子の並列回路数を $a$ 、電機子電流を $I_a$とすると、電機子電流=コイル電流×並列回路数[A]なので、
$I=\displaystyle\frac{I_a}{a}[A]$… (6)
全電機子導体に加わる力 $F$[N]は、$F=fZ$[N]ですので、(5),(6)式より
$F=fZ=\displaystyle\frac{pϕZ}{πD}・\displaystyle\frac{I_a}{a}$[N]
電機子に働くトルクを $T$[N・m]とすると、 $T=F×\displaystyle\frac{D}{2}$[N・m]で表すことができますので、
$T=F×\displaystyle\frac{D}{2}=\displaystyle\frac{pZ}{2πa}ϕI_a=K_2ϕI_a$[N・m]… (7)
ただし、$K_2=\displaystyle\frac{pZ}{2πa}$ はトルク定数
直流電動機の機械的出力を $P_o$[W]とすると、$P_o=EI_a$[W]で表すことができますので、
$P_o=EI_a=\displaystyle\frac{pϕNZ}{60a}I_a=\displaystyle\frac{2πN}{60}×\displaystyle\frac{pZϕI_a}{2πa}$[W]… (8)
ここで、角周波数 $ω$[rsd/s]は、
$ω=\displaystyle\frac{2πN}{60}$[rsd/s]… (9)
ですので、 (8)式は(7),(9)式より、次のように表すことができます。
$P_o=\displaystyle\frac{2πN}{60}×\displaystyle\frac{pZϕI_a}{2πa}=ωT$[W]
直流電動機のトルクを求める式①
$T=\displaystyle\frac{pZ}{2πa}ϕI_a$
$T$[N・m]:回転子に発生するトルク
$Z$:全導体数 (全コイル数)
$a$:並列回路数
$p$:磁極数
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$I_a$[A]:電機子電流
並列回路数 $a$ は、重ね巻では $a=p$、波巻では $a=2$ となります。
直流電動機のトルクを求める式②
$T=K_2ϕI_a$[N・m]
$T$[N・m]:回転子に発生するトルク
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$I_a$[A]:電機子電流
$K_2=\displaystyle\frac{pZ}{2πa}$ :トルク定数(比例定数)
回転速度 $n$ で回転する回転子が、1 秒間に回転する角度を求める式
$ω=\displaystyle\frac{2πn}{60}$
$ω$[rsd/s]:角速度
$n$[min-1]:回転速度
角速度 $ω$、トルク $T$ のときの出力を求める式
$P_o=ωT$[W]
$P_o$[W]:直流電動機の機械的出力
$ω$[rsd/s]:角速度
$T$[N・m]:回転子に発生するトルク
電験三種-機械の過去問解説:直流機の原理と構造
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問1
磁極数 4、電機子導体数 480の直流分巻発電機がある。各磁極の磁束が 0.01[Wb]で、発電機の回転速度が 900[rpm]であったとすれば、この発電機の誘起起電力[V]として、正しいのは次のうちどれか。ただし、電機子巻線は波巻とする。
(1) 72 (2) 134 (3) 144 (4) 246 (5) 288
1997年(平成9年)問1 過去問解説
磁極数を $p$、電機子導体数を $Z$、磁極の磁束を $ϕ$[Wb]、回転数を $n$[rpm]、電機子の並列回路数を $a$ とすると、電機子全体の誘導起電力 $E$[V]は、
$E=\displaystyle\frac{pZϕn}{60a}$[V]
波巻なので、並列回路数は、$a=2$ となり、各数値を公式に代入すると、
$E=\displaystyle\frac{4×480×0.01×900}{60×2}=144$[V]
答え (3)
2006年(平成18年)問1
電機子巻線が重ね巻である 4極の直流発電機がある。電機子の全導対数は 576で、磁極の断面積は 0.025[m2]である。この発電機を回転数 600[min-1]で無負荷運転しているとき、端子電圧は 110[V]である。このときの磁極平均磁束密度[T]の値として、最も近いのは次のうちどれか。
ただし、漏れ磁束は無いものとする。
(1) 0.38 (2) 0.52 (3) 0.64 (4) 0.76 (5) 0.88
2006年(平成18年)問1 過去問解説
磁極数を $p$、電機子導体数を $Z$、磁極の磁束を $ϕ$[Wb]、回転数を $n$[min-1]、電機子の並列回路数を $a$ とすると、電機子全体の誘導起電力 $E$[V]は、
$E=\displaystyle\frac{pZϕn}{60a}$[V]
重ね巻なので、並列回路数は、$a=p=4$ となり、各数値を公式に代入すると、
$110=\displaystyle\frac{4×576×ϕ×600}{60×4}$
$ϕ≒0.019$[Wb]
磁極平均磁束密度 $B$[T]は、磁極の断面積を $S$[m2]とすると、
$B=\displaystyle\frac{ϕ}{S}=\displaystyle\frac{0.019}{0.025}=0.76$[T]
答え (4)
2008年(平成20年)問1
長さ l[m]の導体を磁束密度 B[T]の磁束の方向と直角に置き、速度 v[m/s]で導体及び磁束に直角な方向に移動すると、導体にはフレミングの( ア )の法則によって、 e =( イ )[V]の誘導起電力が発生する。
1極あたりの磁束がφ[Wb]、磁極数が p、電機子導体数が Z、巻線の並列回路数が a,電機子の直径が D[m]なる直流機が速度 n[min-1]で回転しているとき、周辺速度は $v=πD\displaystyle\frac{n}{60}$[m/s]となり、直流機の正負のブラシ間には( ウ ) 本の導体が( エ )に接続されるので、電機子の誘導起電力は、E=( オ )[V]となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる語句又は式として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 右手 | $Blv$ | $\displaystyle\frac{Z}{a}$ | 直列 | $\displaystyle\frac{pZ}{60a}ϕn$ |
| (2) | 左手 | $Blv$ | $Za$ | 直列 | $\displaystyle\frac{pZa}{60}ϕn$ |
| (3) | 右手 | $\displaystyle\frac{Bv}{l}$ | $Za$ | 並列 | $\displaystyle\frac{pZa}{60}ϕn$ |
| (4) | 右手 | $Blv$ | $\displaystyle\frac{a}{Z}$ | 並列 | $\displaystyle\frac{pZ}{60a}ϕn$ |
| (5) | 左手 | $\displaystyle\frac{Bv}{l}$ | $\displaystyle\frac{Z}{a}$ | 直列 | $\displaystyle\frac{Z}{60pa}ϕn$ |
2008年(平成20年)問1 過去問解説
長さ l[m]の導体を磁束密度 B[T]の磁束の方向と直角に置き、速度 v[m/s]で導体及び磁束に直角な方向に移動すると、導体にはフレミングの( 右手 )の法則によって、 e =( $Blv$ )[V]の誘導起電力が発生する。
1極あたりの磁束がφ[Wb]、磁極数が p、電機子導体数が Z、巻線の並列回路数が a,電機子の直径が D[m]なる直流機が速度 n[min-1]で回転しているとき、周辺速度は $v=πD\displaystyle\frac{n}{60}$[m/s]となり、直流機の正負のブラシ間には( $\displaystyle\frac{Z}{a}$ ) 本の導体が( 直列 )に接続されるので、電機子の誘導起電力は、E=( $\displaystyle\frac{pZ}{60a}ϕn$ )[V]となる。
答え (1)
2012年(平成24年)問1
次の文章は、直流機の構造に関する記述である。
直流機の構造は、固定子と回転子とからなる。固定子は、( ア )、継鉄などによって、また、回転子は、( イ )、整流子などによって構成されている。
電機子鉄心は、( ウ )磁束が通るため、( エ )が用いられている。また、電機子巻線を収めるための多数のスロットが設けられている。
六角形(亀甲形)の形状の電機子巻線は、そのコイル辺を電機子鉄心のスロットに挿入する。各コイル相互のつなぎ方には、( オ )と波巻とがある。直流機では、同じスロットにコイル辺を上下に重ねて2個ずつ入れた二層巻としている。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 界磁 | 電機子 | 交番 | 積層鉄心 | 重ね巻 |
| (2) | 界磁 | 電機子 | 一定 | 積層鉄心 | 直列巻 |
| (3) | 界磁 | 電機子 | 一定 | 鋳 鉄 | 直列巻 |
| (4) | 電機子 | 界 磁 | 交番 | 鋳 鉄 | 重ね巻 |
| (5) | 電機子 | 界 磁 | 一定 | 積層鉄心 | 直列巻 |
2012年(平成24年)問1 過去問解説
直流機の構造は、固定子と回転子とからなる。固定子は、( 界磁 )、継鉄などによって、また、回転子は、( 電機子 )、整流子などによって構成されている。
電機子鉄心は、( 交番 )磁束が通るため、( 積層鉄心 )が用いられている。また、電機子巻線を収めるための多数のスロットが設けられている。
六角形(亀甲形)の形状の電機子巻線は、そのコイル辺を電機子鉄心のスロットに挿入する。各コイル相互のつなぎ方には、( 重ね巻 )と波巻とがある。直流機では、同じスロットにコイル辺を上下に重ねて2個ずつ入れた二層巻としている。
答え (1)
2013年(平成25年)問2
図は、磁極数が 2 の直流発電機を模式的に表したものである。電機子巻線については、1巻き分のコイルを示している。電機子の直径 D は 0.5[m]、電機子導体の有効長 l は 0.3[m]、ギャップの磁束密度 B は、図の状態のように電機子導体が磁極の中心付近にあるとき一定で 0.4[T]、回転速度 n は 1200[min-1]である。図の状態におけるこの1巻きのコイルに誘導される起電力 e[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
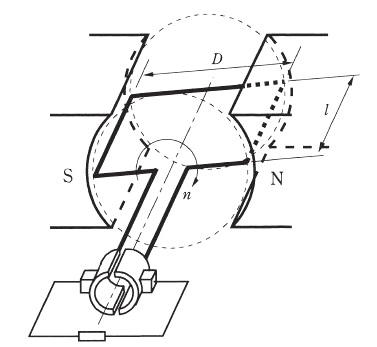
(1) 2.40 (2) 3.77 (3) 7.54 (4) 15.1 (5) 452
2013年(平成25年)問2 過去問解説
コイル辺の周速度を $v$[m/s]は、コイルの直径を $D$[m]、コイルの回転速度を $n$[min-1]とすると、
$v=ωr=\displaystyle\frac{2πn}{60}×\displaystyle\frac{D}{2}=\displaystyle\frac{πDN}{60}$
$=\displaystyle\frac{π×0.5×1200}{60}=10π$[m/s]… (2)
フレミング右手の法則よりコイルの誘導起電力は
$e_1=Blv$[V]
ただし、コイルは2辺あるので2倍になります。したがって求める起電力 $e$[V]は、
$e=2Blv=2×0.4×0.3×10π≒7.54$[V]
答え (3)
2015年(平成27年)問1
4極の直流電動機が電機子電流 250A、回転速度 1200min-1 で一定の出力で運転されている。電機子導体は波巻であり、全導体数が 258、1極当たりの磁束が 0.020 Wbであるとき、この電動機の出力の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、波巻の並列回路数は 2 である。また、ブラシによる電圧降下は無視できるものとする。
(1) 8.21 (2) 12.9 (3) 27.5 (4) 51.6 (5) 55.0
2015年(平成27年)問1 過去問解説
電機子電流を $I_a$[A]、回転速度を $n$[min-1 ]、全導体数を $Z$、1極当たりの磁束を $ϕ$[Wb]、極数を $p$、並列回路数を $a$ とすると、直流電動機の機械的出力を $P_o$[W]は、
$P_o=EI_a=\displaystyle\frac{pϕnZ}{60a}I_a$
$=\displaystyle\frac{4×0.020×1200×258}{60×2}×250=51.6$[kW]
答え (4)
電験三種の機械科目に出題される「直流機」のページ
- 直流機の原理と構造
- 直流機の電機子反作用
- 直流発電機の種類と特性
- 直流電動機の種類と特性
- 直流電動機の始動と速度制御
- 直流機の定格






