特殊変圧器と計器用変成器

このページでは、特殊変圧器と計器用変成器について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された特殊変圧器と計器用変成器の過去問題の解き方も解説しています。

単巻変圧器

単巻変圧器は、図1に示すように、巻線は一つしかなく、巻線の一部から端子が出ています。図において、巻線の共通部分abを分路巻線、共通でない部分bcを直列巻線といいます。

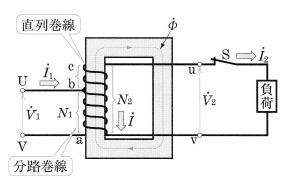
分路巻線の巻数を $N_1$、全体の巻数を $N_2$ とすると、分路巻線に加える電圧 $\dot{V}_1$［V］と、全体の巻線に誘導される電圧 $\dot{V}_2$［V］との間には、次の関係がなりたちます。

$\displaystyle\frac{\dot{V}_1}{\dot{V}_2}=\displaystyle\frac{N_1}{N_2}=a$ … (1)

次に、二次側端子u，v間に負荷を接続したとき、流れる負荷電流を $\dot{I}_2$［A］、一次側に流れる電流を $\dot{I}_1$［A］とし、巻線の励磁電流を無視すると、$\dot{I}_1$ と $\dot{I}_2$ の間には、次の関係がなりたちます。

$N_1(I_1-I_2)=(N_2-N_1)I_2$

$\displaystyle\frac{I_1}{I_2}=\displaystyle\frac{N_2}{N_1}=\displaystyle\frac{1}{a}$ … (2)

また、分路巻線に流れる電流 $\dot{I}$［A］は、次の式で表すことができます。

$I=I_1-I_2=(1-a)I_1$ … (3)

単巻変圧器は、分路巻線を一次巻線、直列巻線を二次巻線として、ふつうの変圧器のように動作しますので、その容量 $P_S$［V･A］は、次の式で表すことができます。

$P_S=(V_2-V_1)I_2=(1-a)V_2I_2$ … (4)

$P_S$ は、変圧器自身の容量ですので、自己容量とよばれていまる。図1において、二次端子u，vから取り出せる出力 $P_l$［V･A］は、次の式で表すことができます。

$P_l=V_2I_2$ … (5)

この $P_l$ を負荷容量といいます。単巻変圧器の定格容量は、自己容量や負荷容量で表されます。なお、単巻変圧器は、一次巻線・二次巻線が共通であるため、漏れ磁束が少なく、電圧変動率も小さいのが特徴です。したがって、効率がよいので、二相結線にして電力系統の電圧調整や、小容量の滑り電圧調整器などに広く使われています。しかし、一次巻線と二次巻線が共通であるため、変圧比が大きくなると危険です。

三巻線変圧器

図2(a)に示すように、三つの巻線をもつ変圧器を三巻線変圧器といい、それぞれの巻線を一次巻線・二次巻線・三次巻線といいます。図(b)は二次側を一次側に換算した等価回路です。

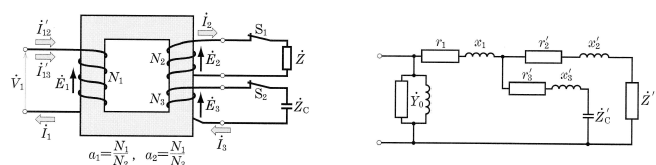
三巻線変圧器は、単相のまま用いるほか、三相結線されて次のような場合に用いらています。

一次・二次をY一Y結線にして、三次を△結線(安定巻線ともいう)として使用する。
送電線の終端に設置し、三次巻線に調相機や進相用コンデンサを接続し、一次回路の力率改善と電圧調整をして定電圧送電を行う。
二つの巻線を一次として電圧の異なった2系統から受電し、残りの巻線を二次として負荷に送電する。
一次で受電し、二次巻線および三次巻線の2系統で異なる電圧の電力を供給する。

磁気漏れ変圧器

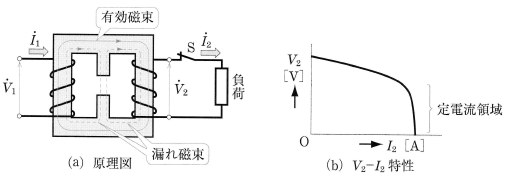
図3(a)に示すように、磁路の一部にギャップがある鉄心に、一次巻線・二次巻線を巻いた変圧器を磁気漏れ変圧器といいます。この変圧器では、図(b)に示すように、負荷電流 $I_2$［A］が増加すると、漏れ磁束が増加し、二次側端子電圧が急激に減少します。このような特性を示す領域では、電圧が変わっても負荷電流が一定に保たれます。したがって、この特性は定電流特性とよばれます。磁気漏れ変圧器は、定電流特性をもつため、蛍光灯安定器，ネオンを点灯するためのネオン管用変圧器，アーク溶接機用変圧器などに用いられます。

計器用変成器

送配電系統の高電圧・大電流を一般の指示計器を用いて直接測定することは危険です。このような場合には、高圧回路と絶縁し、低電圧・小電流に変成して測定します。このために用いる変圧器を計器用変成器といい、変流器と計器用変圧器があります。

変流器

図4に示すのは、一次巻線・二次巻線の巻線がそれぞれ $N_1$，$N_2$ の変圧器です。一次巻線に被測定電流 $I_2$［A］を流し、二次電流 $I_2$［A］を電流計Aで測定すると、$I_1$は、次の式から求めることができます。

$I_1=\displaystyle\frac{N_2}{N_1}I_2=\displaystyle\frac{1}{a}I_2=KI_2$ … (6)

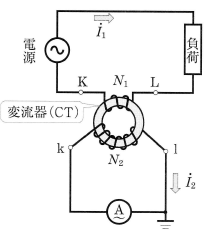
たとえば、$N_1=10$，$N_2=100$ とすれば、$I_1=10I_2$ となります。そこで、$I_2=2$A であれば、$I_1=20$A となります。つまり、電流計Aが 2A を示しているときには、$I_1$ は 20A であることがわかります。したがって、電流計Aの最大目盛が 5A であれば、50A まで測定できるようになります。このような目的で用いられる変圧器は、変流器(CT)とよばれ、$K$ の値は変流比といいます。

負担

変流器の負荷は電流計や電力計などです。変流器の二次定格電流は 1A または 5A に決められていますので、交流電流計を接続する場合、変流器の定格電流に合わせた最大目盛 1A または 5A の端子につなぐことになります。この場合、計器ならびに配線のインピーダンスを 1.6Ω とすれば、その皮相電力は 5× 5× 1.6=40VA となります。このように、変流器から負荷に供給される皮相電力を負担といいます。一般に変流器を使用するときには、この負担に注意しなければなりません。

なお、通電中にCTの二次側から計器を取り外す場合には、必ず二次側を短絡しておかなければなりません。二次側を開放のままで、一次側に被測定電流を流すと、被測定電流がすべて励磁電流となり、CTのコイルに高圧が発生し、焼損するおそれがあります。また、焼損しなくても人体に危険です。

計器用変圧器

図5に示すのは、一次巻線・二次巻線の巻線がそれぞれ $N_1$，$N_2$ の変圧器です。一次側に被測定電圧 $V_1$［V］を加え、二次電圧 $V_2$［V］を電圧計Vで測定すると、$V_1$は、次の式から求めることができます。

$V_1=\displaystyle\frac{N_1}{N_2}V_2=KV_2$ … (6)

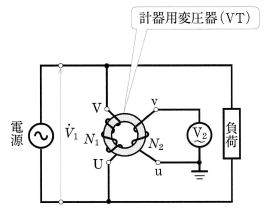
たとえば、$\displaystyle\frac{N_1}{N_2}=100$ であれば、電圧計Vが 100V を指示しているときには、被測定電圧 $V_1=10000$V であることがわかります。このような目的で用いられる変圧器は、計器用変圧器(VT)とよばれ、$K$ の値は変圧比といいます。

負担変流器の場合と同様に、計器用変圧器から負荷に供給される皮相電力［V･A］を負担といいます。計器用変圧器の二次定格電圧は 110V または、$\displaystyle\frac{110}{\sqrt{3}}$V に統一されており、電圧計には最大目盛が 150V と $\displaystyle\frac{150}{\sqrt{3}}$V のものが用いられています。電圧が 110V で、負担が 100V・A であれば、負荷インピーダンスは 121V となります。

CT，VTを用いる利点

CT，VTを用いると、電流・電圧の測定範囲を拡大することができます。CT，VTを用いる利点として、次のことがあげられます。

通常の計器の使用
大電流や高電圧をはかる必要がある場合でも、最大目盛が 5A，150V というような通常の電流計や電圧計を用いることができる。
測定の安全
大電流・高電圧の回路から絶縁された二次回路で、測定ができるので安全である。
遠隔測定
二次回路を長くすれば、実際の回路から離れた場所で測定ができるので、計測の集中管理などに便利である。

電験三種－機械（変圧器）過去問

1998年（平成10年）問4

定格一次電圧 200［V］、定格二次電圧 160［V］の単相単巻変圧器がある。この変圧器の一次側を 200［V］の交流電源に接続し、二次側に負荷を接続したところ、分路巻線には 5［A］の電流が流れた。このときの直列巻線の電流［A］の値として、正しいのは次のうちどれか。ただし、励磁電流は無視するものとする。

(1) 1.3　(2) 6.3　(3) 11　(4) 20　(5) 25

1998年（平成10年）問4　過去問解説

一次回路と二次回路の電圧の比および電流の比より、

$\displaystyle\frac{V_1}{V_2}=\displaystyle\frac{I_2}{I_1}$

分路巻線の電流の大きさを $I$［A］とすると、$I_1=I+I_2$ ですので、

$\displaystyle\frac{V_1}{V_2}=\displaystyle\frac{I_2}{I+I_2}$

$\displaystyle\frac{200}{160}=\displaystyle\frac{I_2}{I+I_2}$

$I_2=20$［A］

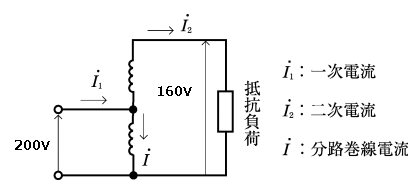
答え (4)

2000年（平成12年）問9

図のような定格一次電圧 100［V］、定格二次電圧 120［V］の単相単巻変圧器があり、無負荷で一次側に 100［V］の電圧を加えたときの励磁電流は 1［A］であった。この変圧器の二次側に抵抗負荷を接続し、一次側を 100［V］の電源に接続して二次側に大きさが 15［A］の電流が流れたとき、分路巻線電流の大きさの値として、正しいのは次のうちどれか。　
ただし、巻線の抵抗及び漏れリアクタンス並びに鉄損は無視できるものとする。

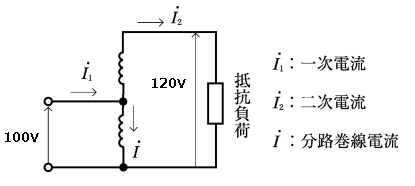
(1) 2　(2) 2$\sqrt{2}$　(3) $\sqrt{10}$　(4) 5　(5) $\sqrt{19}$

2000年（平成12年）問9　過去問解説

一次回路と二次回路の電圧の比および電流の比より、

$\displaystyle\frac{V_1}{V_2}=\displaystyle\frac{I_2}{I_1}$

$\displaystyle\frac{100}{120}=\displaystyle\frac{15}{I_1}$

$I_1=18$［A］

このときの、分路巻線電流 $\dot{I}$［A］の、電圧同相分の大きさを $I’$［A］とすると、

$I’=I_1-I_2=18-15=3$［A］

無負荷の励磁電流 $I_o$ は、電圧より90°位相が遅れますので、分路巻線電流の大きさ $I$［A］は、

$I=\sqrt{{I’}^2+{I_o}^2}=\sqrt{3^2+1^2}=\sqrt{10}$

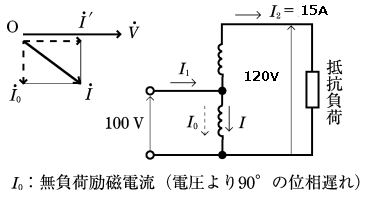
答え (3)

2005年（平成17年）問7

図のような単巻変圧器において、分路巻線の巻き数を $N_1$、直列巻線の巻数を $N_2$ とし、一次側に流れる電流を $I_1$、負荷側に流れる電流を $I_2$ としたときに、次の関係式のうち正しいものはどれか。
ただし、励磁電流、巻線内の損失及び電圧降下は無視するものとする。

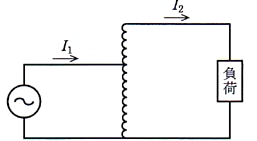
(1) $N_1I_1＝(N_1＋N_2)I_2$
(2) $N_1/N_2＝I_1/I_2$
(3) $(N_2−N_1)I_1＝N_2I_2$
(4) $N_1I_1＝N_2I_2$
(5) $N_1I_2＝(N_1＋N_2)I_1$

2005年（平成17年）問7　過去問解説

図を等価な二巻線変圧器と考えると、一次入力=二次出力なので、(1)の等式が正しくなります。

答え (1)

2007年（平成19年）問6

図に示すように、定格一次電圧 6000［V］、定格二次電圧 6600［V］の単相単巻変圧器がある。消費電力 100［kW］、力率 75［%］(遅れ)の単相負荷に定格電圧で電力を供給するために必要な単巻変圧器の自己容量［kV･A］として、最も近いのは次のうちどれか。
ただし、巻線の抵抗、漏れリアクタンス及び鉄損は無視できるものとする。

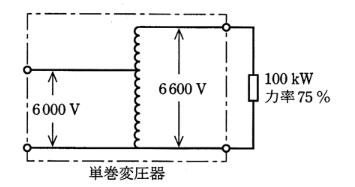
(1) 9.1　(2) 12.1　(3) 100　(4) 121　(5) 133

2007年（平成19年）問6　過去問解説

負荷電流を $I_2$［A］とすると、

$I_2=\displaystyle\frac{P}{Vcosθ}=\displaystyle\frac{100×10^3}{6600×0.75}≒20.2$［A］

自己容量 $P_S$［kV･A］は、

$P_S=(V_2-V_1)I_2=(6600-6000)×20.2≒12.1$［kV･A］

答え (2)

2010年（平成22年）問8

単相変圧器 3 台が図に示すように 6.6［kV］電路に接続されている。一次側は星形(Y)結線、二次側は開放三角結線とし、一次側中性点は大地に接続され、二次側開放端子には図のように抵抗 $R_o$ が負荷として接続されている。三相電圧が平衡している通常の状態では、各相が打ち消しあうため二次側開放端子には電圧は現れないが、電路のバランスが崩れ不平衡になった場合や電路に地絡事故などが発生した場合には、二次側開放端子に電圧が現れる。このとき、二次側の抵抗負荷 $R_o$ は各相が均等に負担することになる。

いま、各単相変圧器の定格一次電圧が $\displaystyle\frac{6.6}{\sqrt{3}}$［kV］、定格二次電圧が $\displaystyle\frac{110}{\sqrt{3}}$［V］で、二次接続抵抗点 $R_o=10$［Ω］の場合、一次側に換算した 1 相当たりの二次抵抗［kΩ］の値として、最も近いのは次のうちどれか。
ただし、変圧器は理想変圧器であり、一次巻線，二次巻線の抵抗及び損失は無視するものとする。

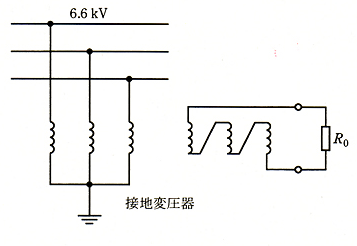
(1) 4.00　(2) 6.93　(3) 12.0　(4) 20.8　(5) 36.0

2010年（平成22年）問8　過去問解説

非接地式の 6.6KV 系の配電線路には、地絡事故を検出する目的で、変電所にGPT（接地形計器用変圧器）が設けられています。

GPTの二次側回路は、抵抗 $R_o$ により、$\displaystyle\frac{R_o}{3}$ の制限抵抗と地絡過電圧継電器から構成された回路になります。GPTの一次側・二次側の巻線比を $n:1$ とすると、二次側抵抗 $\displaystyle\frac{R_o}{3}$ を一次側に換算すると、$R_1=n^2\displaystyle\frac{R_o}{3}$ となります。

$n=\displaystyle\frac{\displaystyle\frac{60}{\sqrt{3}}}{\displaystyle\frac{110}{\sqrt{3}}}=60$

$R_1=n^2\displaystyle\frac{R_o}{3}=60^2×\displaystyle\frac{10}{3}=12.0$［kΩ］

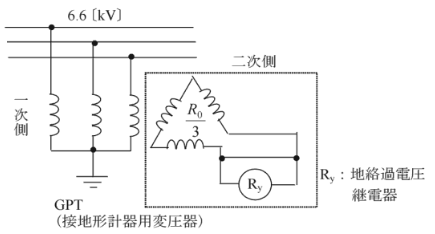
答え (3)

2013年（平成25年）問8

次の文章は、単相単巻変圧器に関する記述である。

巻線の一部が一次と二次との回路に共通になっている変圧器を単巻変圧器という。巻線の共通部分を（　ア　）、共通でない部分を（　イ　）という。単巻変圧器では、（　ア　）の端子を一次側に接続し、（　イ　）の端子を二次側に接続して使用すると通常の変圧器と同じように動作する。単巻変圧器の（　ウ　）は、二次端子電圧と二次電流との積である。単巻変圧器は、巻線の一部が共通であるため、漏れ磁束が（　エ　）、電圧変動率が（　オ　）。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

	（ア）	（イ）	（ウ）	（エ）	（オ）
(1)	分路巻線	直列巻線	負荷容量	多く	小さい
(2)	直列巻線	分路巻線	自己容量	少なく	小さい
(3)	分路巻線	直列巻線	定格容量	多く	大きい
(4)	分路巻線	直列巻線	負荷容量	少なく	小さい
(5)	直列巻線	分路巻線	定格容量	多く	大きい

2013年（平成25年）問8　過去問解説

巻線の一部が一次と二次との回路に共通になっている変圧器を単巻変圧器という。巻線の共通部分を（　分路巻線　）、共通でない部分を（　直列巻線　）という。単巻変圧器では、（　分路巻線　）の端子を一次側に接続し、（　直列巻線　）の端子を二次側に接続して使用すると通常の変圧器と同じように動作する。単巻変圧器の（　負荷容量　）は、二次端子電圧と二次電流との積である。単巻変圧器は、巻線の一部が共通であるため、漏れ磁束が（　少なく　）、電圧変動率が（　小さい　）。

答え (4)

2016年（平成28年）問7

各種変圧器に関する記述として、誤っているものを次の(1)～(5)のうちから一つ選べ。

単巻変圧器は、一次巻線と二次巻線とが一部分共通になっている。そのため、一次巻線と二次巻線との間が絶縁されていない。変圧器自身の自己容量は、負荷に供給する負荷容量に比べて小さい。
三巻線変圧器は、一つの変圧器に三組の巻線を設ける。これを3台用いて三相Y－Y結線を行う場合、一組目の巻線をY結線の一次、二組目の巻線をY結線の二次、三組目の巻線をΔ結線の第3調波回路とする。
磁気漏れ変圧器は、磁路の一部にギャップがある鉄心に、一次巻線及び二次巻線を巻く。負荷のインピーダンスが変化しても、変圧器内の漏れ磁束が変化することで、負荷電圧を一定に保つ作用がある。
計器用変成器には、変流器（CT）と計器用変圧器（VT）がある。これらを用いると、大電流又は高電圧の測定において、例えば最大目盛りが5A、150Vという通常の電流計又は電圧計を用いることができる。
変流器（CT）では、電流計が二次側の閉回路を構成し、そこに流れる電流が一次側に流れる被測定電流の起磁力を打ち消している。通電中に誤って二次側を開放すると、被測定電流が全て励磁電流となるので、鉄心の磁束密度が著しく大きくなり、焼損するおそれがある。