第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「三相同期発電機の等価回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「三相同期発電機の等価回路」の過去問題も解説しています。
電機子反作用
同期発電機が負荷に電力を供給して、発電機の電機子巻線に電機子電流が流れると、この電流により回転磁界が発生して主磁束を乱す作用を及ぼします。この作用によって誘導起電力が変化します。この現象を、同期発電機における電機子反作用といいます。直流発電機の場合と違って、負荷の力率によって、異なった電機子反作用が生じます。
交さ磁化作用
三相同期発電機に抵抗の負荷のみが接続されている場合は、力率が 1 で運転されています。この場合の電機子反作用を考えてみます。
図1のようにa相のみを考え、図(a)のa相の起電力 $e_a$[V]が最大値のとき、電機子電流 $i_a$[A]も最大になり、このときの電機子巻線と磁極との位置関係、および電機子巻線がつくる回転磁界の分布は図(b)のようになります。
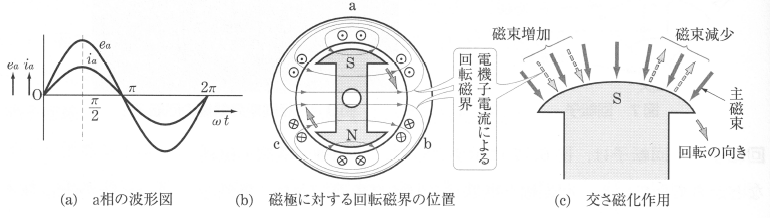
すなわち、電機子電流による回転磁界の軸は、図(b)に示すように、つねに主磁束の軸に垂直であり、これらの磁束は磁極面に対して図(c)のように、右側で磁束を減少させ、左側では磁束を増加させます。このような作用を「交さ磁化作用」といいます。
減磁作用
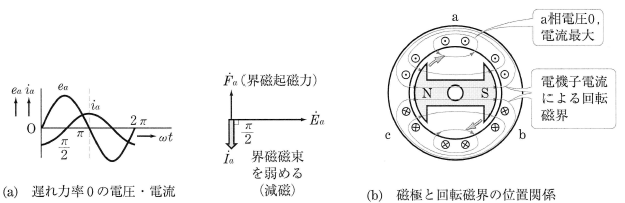
発電機にリアクトルの負荷のみが接続されている場合は、遅れ力率が 0 で運転されています。この場合は、図2(a)のようにa相の起電力($e_a$)が 0V のとき、電機子電流($i_a$[A])は正の最大になっています。このときの電機子巻線と磁極との位置関係、および回転磁界の分布は図(b)のようになり、回転磁界は主磁束の向きと逆になって主磁束を減少させてしまいます。このような現象を「減磁作用」といいます。
増磁作用
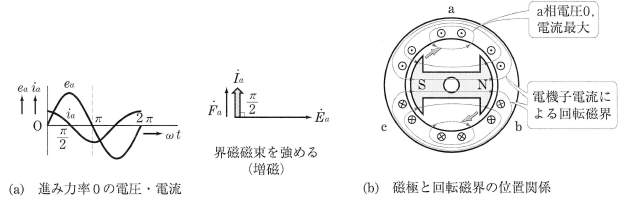
発電機にコンデンサの負荷のみが接続されている場合は、進み力率が 0 で運転されています。この場合は、図3(a)のようにa相の起電力が 0 のとき、電機子電流は負の最大になっています。このときの電機子巻線と磁極との位置関係、および回転磁界の分布は図(b)のようになり、回転磁界と主磁束は同一の向きで重なり合い、磁束を増加させる作用が生じます。このような現象を「増磁作用」といいます。
一般に、電機子電流 $\dot{I}$[A]の位相が、誘導起電力 $\dot{E}$[V]に対して、$θ$[rad]であるときの電機子反作用は、電流の有効分 $Icosθ$ によって交さ磁化作用が働き、無効分 $Isinθ$ によって、電流が遅れ電流であれば減磁作用、進み電流であれば増磁作用として働きます。
同期発電機の電機子反作用
- 電機子巻線に発生する磁束が界磁磁束に影響を与え、起電力を変化させる事
起電力 E と 負荷電流 I の位相差による電機子反作用の違い
- 起電力 E と 負荷電流 I が同相・・・交差磁化作用
- 負荷電流 I が90°遅れ・・・減磁作用 (起電力減少)
- 負荷電流 I が90°進み・・・増磁作用( 起電力増加)
自己励磁現象
同期発電機が無負荷の長距離高圧送電線路(容量負荷など)に接続されていると、静電容量のため無励磁で運転しても進みの無効電流が流れます。この電流による電機子反作用は増磁作用となり、端子電圧が上昇します。この場合の電機子電流と端子電圧の関係は、図6のようになります。
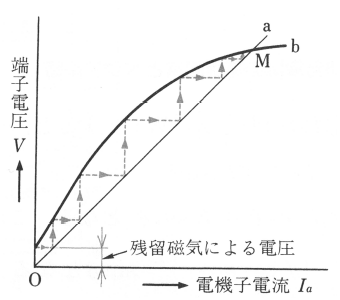
つまり、直線 oa は、静電容量の容量負荷に流れる電流と、負荷の端子電圧の関係を示し、曲線bは無負荷飽和曲線を示します。電流がゼロの場合でも発電機の残留磁気によってわずかな電圧が発生し、発電機に進み電流が流れます。そのため、電機子反作用(増磁作用)が発生し、電圧は上昇して、進み電流はいっそう増加し、さらに電圧は上昇します。このようなことを繰り返して、電圧はM点に落ちつきます。
このように無励磁の同期発電機に進み電流が流れ、電圧を上昇させる現象を同期発電機の「自己励磁現象」といいます。なお、点Mの電圧が発電機の定格より非常に大きければ、巻線の絶縁を破壊するおそれがあります。
発電機の等価回路
同期発電機の電機子反作用を回路要素に置き換えた等価回路を用いると、発電機の誘導起電力と端子電圧の関係を理解するうえでたいへん便利です。そこで、電機子反作用を考慮した発電機の等価回路について考えてみます。
電機子反作用によるリアクタンス
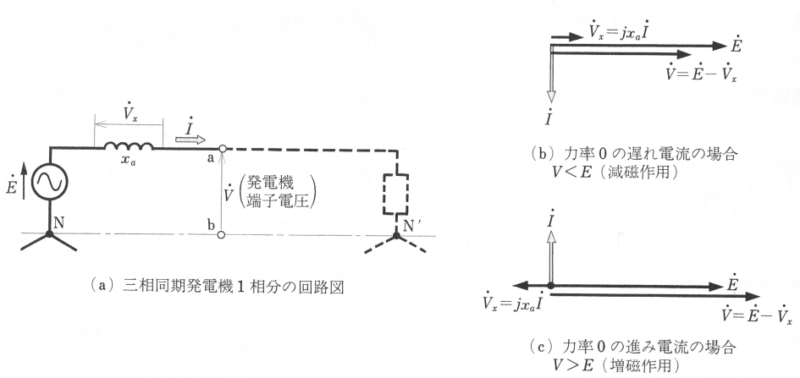
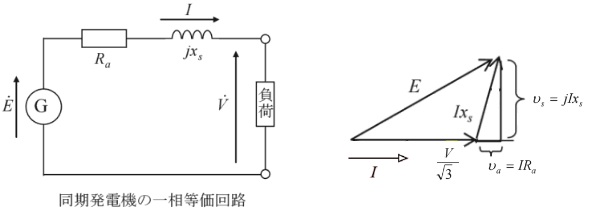
図4(a)は、三相同期発電機の誘導起電力 $\dot{E}$[V]に直列にリアクタンス $x_a$[Ω]を接続したもので、電機子電流 $\dot{I}$[A]が流れると、次の関係がなりたちます。
$\dot{V_x}=jx_a\dot{I}$
$\dot{V} =\dot{E}-\dot{V_x}$
いま、電機子電流 $\dot{I}$[A]が力率 0 の遅れ電流のとき、端子電圧 $\dot{V}$[V]はベクトル図(b)から求めることができます。また、電機子電流 $\dot{I}$[A]が力率 0 の進み電流のときは、図(c)から求めることができます。すなわち、$\dot{E}$[V]を主磁束による誘導起電力とすれば、電機子反作用としての減磁作用・増磁作用による起電力の増減は、リアクタンス $x_a$[Ω]に生じる電圧降下 $\dot{V_x}$[V]で表すことができます。そこで、$x_a$[Ω]は「電機子反作用によるリアクタンス」とよばれます。
同期リアクタンス
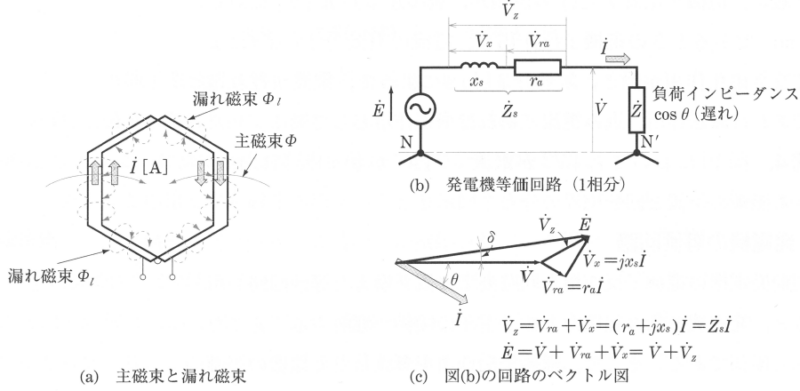
電機子電流がつくる磁束の中で、図5(a)に示すように、その磁路が主磁束の磁路を通らない漏れ磁束 $ϕ_l$[Wb]があります。この漏れ磁束によって生じる電圧降下は、リアクタンス $x_l$[Ω]に置き換えられ、漏れリアクタンスとよんでいます。
また、$x_a$[Ω]と $x_l$[Ω]の和 $x_s$[Ω]は「同期リアクタンス」とよばれ、$x_s=x_a+x_l$[Ω]で表されます。
同期リアクタンスの公式
$x_s=x_a+x_l$
$x_s$[Ω]:同期リアクタンス
$x_a$[Ω]:電機子反作用によるリアクタンス
$x_l$[Ω]:漏れリアクタンス
同期インピーダンス
$r_a$[Ω]を電機子巻線抵抗とすると、三相同期発電機1相分の等価回路は図5(b)のようになり、そのインピーダンス $\dot{Z_s}$[Ω]は、次の式で表すことができます。
$\dot{Z_s}=r_a+jx_s$[Ω]
$Z_s=\sqrt{{r_a}^2+{x_s}^2}$
この $\dot{Z_s}$[Ω]、$Z_s$[Ω]は同期インピーダンスとよばれています。図(c)は、ある負荷電流における同期発電機のベクトル図です。
同期インピーダンスの公式
$\dot{Z_s}=r_a+jx_s$
$Z_s=\sqrt{{r_a}^2+{x_s}^2}$
$\dot{Z_s}$[Ω]:同期インピーダンス
$r_a$[Ω]:巻線抵抗
$x_l$[Ω]:同期リアクタンス
電験三種-機械の過去問解説:三相同期発電機の等価回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1998年(平成10年)問3
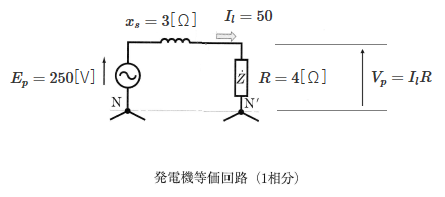
星形結線の非突極形三相同期発電機があり、各相の同期リアクタンスが 3[Ω]、無負荷時の出力端子と中性点間の電圧が 250[V]である。この発電機に純抵抗からなる三相平衡負荷を接続し、線電流 50[A]を流したときの端子電圧[V]の値として、正しいのは次のうちどれか。ただし、電機子巻線抵抗は無視するものとする。
(1) 173 (2) 200 (3) 283 (4) 346 (5) 433
1998年(平成10年)問3 過去問解説
発電機出力電圧を $E_p$[V]、線電流を $I_l$[A]とすると、1相のインピーダンス $Z$[Ω]は、
$Z=\displaystyle\frac{E_p}{I_l}=\displaystyle\frac{250}{50}=5$[Ω]
1相のリアクタンスを $x_s$[Ω]とすると、負荷抵抗を $R$[Ω]は、
$R=\sqrt{Z^2-{x_s}^2}=\sqrt{5^2-3^2}=4$[Ω]
負荷側の線間電圧を $V_l$[V]、相電圧を $V_p$[V]とすると、
$V_l=\sqrt{3}V_p=\sqrt{3}V_pI_lR=\sqrt{3}×50×4≒346$[V]
答え (4)
2005年(平成17年)問6
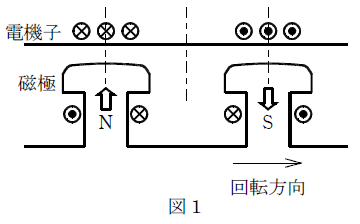
三相同期発電機に平衡負荷をかけ,電機子巻線に三相交流電流が流れると,同期速度で回転する回転磁界が発生し磁極がつくる界磁磁束との間に電機子反作用が生じる。図1は力率が 100[%]で誘導起電力の最大値と電機子電流の最大値が一致したときの磁極 N、S と、電機子電流が最大となる電機子巻線の位置との関係を示す。この図において、N、S 両磁極の右側では界磁磁束を( ア )させ、左側では( イ )させる交さ磁化作用の現象が起きる。図2は、( ウ )力率角がほぼ 1/2π[rad]の場合の磁極N、S と、電機子電流が最大となる電機子巻線の位置との関係を示す。磁極 N、S による磁束は、電機子電流によりいずれも( エ )を受ける。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する語句として、正しいものを組み合わせたのはつぎのうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 増加 | 減少 | 進み | 減磁作用 |
| (2) | 増加 | 減少 | 進み | 磁化作用 |
| (3) | 減少 | 増加 | 遅れ | 減磁作用 |
| (4) | 増加 | 減少 | 遅れ | 磁化作用 |
| (5) | 減少 | 増加 | 遅れ | 磁化作用 |
2005年(平成17年)問6 過去問解説
電機子反作用による磁束が主磁束に影響を及ぼすことを述べています。図1において、電機子反作用の磁束は下向きとなるため、N極の右側では主磁束を打ち消す方向となり、S極の左側では主磁束と同じ方向になって増加する方向になります。図2は、 遅れ力率が 1/2π[rad]で,図1の電機子コイルを 90°左へずらした形になっています。 電機子反作用の磁束は下向きとなるため、主磁束を打ち消す方向となり、減磁作用となります。
答え (3)
2008年(平成20年)問5
定格容量 3300[kV・A]、定格電圧 6600[V]、星形結線の三相同期発電機がある。この発電機の電機子巻線の一相当たりの抵抗は 0.15[Ω]、同期リアクタンスは 12.5[Ω]である。この発電機を負荷力率 100[%]で定格運転したとき、一相当たりの内部誘導起電力[V]の値として、最も近いのは次のうちどれか。
ただし、磁気飽和は無視できるものとする。
(1) 3050 (2) 4670 (3) 5280 (4) 7460 (5) 9150
2008年(平成20年)問5 過去問解説
一相等価回路図とベクトル図を示します。
三相同期発電機の定格容量を $P$[V・A]、定格電圧を $V$[V]とすれば、定格電流 $I$[A]は、
$P=\sqrt{3}VI$
$I=\displaystyle\frac{P}{\sqrt{3}V}==\displaystyle\frac{3300×10^3}{\sqrt{3}×6600}≒288.7$[A]
電機子巻線抵抗を $R_a$[Ω]、同期リアクタンスを $x_s$[Ω]とすると、一相分抵抗の電圧降下 $v_a$[V]と一相分リアクタンスの電圧降下 $v_s$[V]は、
$v_a=IR_a=288.7×0.15≒43.3$[V]
$v_s=jIx_s=j288.7×12.5≒j3609$[V]
定格電圧の相電圧は、
$\displaystyle\frac{V}{\sqrt{3}}=\displaystyle\frac{6600}{\sqrt{3}}≒3811$[V]
ベクトル図より、1相当たりの内部誘導起電力 $E$[V]は、
$E=\sqrt{(\displaystyle\frac{V}{\sqrt{3}}+v_a)^2+v_s^2}$
$=\sqrt{(3811+43.3)^2+3609^2}≒5280$[V]
答え (3)
2011年(平成23年)問4
Y結線の非突極形三相同期発電機があり、各相の同期リアクタンスが 3[Ω]、無負荷時の出力端子と中性点間の電圧が 424.2[V]である。この発電機に1 相当たり $R+ jX_L $[Ω]の三相平衡 Y 結線の負荷を接続したところ各相に 50[A]の電流が流れた。接続した負荷は誘導性でそのリアクタンス分は 3[Ω]である。ただし、励磁の強さは一定で変化しないものとし、電機子巻線抵抗は無視するものとする。
このときの発電機の出力端子間電圧[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)300 (2)335 (3)475 (4)581 (5)735
2011年(平成23年)問4 過去問解説
等価回路図と線電流 $I$ を基準とした、ベクトル図を示します。
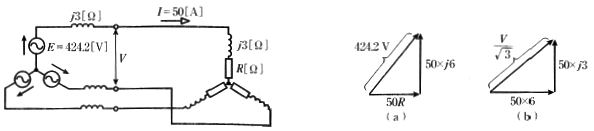
(a)のベクトル図より $R$[Ω]を求めます。
$(50R)^2+(50×6)^2=424.2^2$
$R=\displaystyle\frac{1}{50}\sqrt{424.2^2-(50×6)^2}≒6$[Ω]
発電機の出力端子間電圧 $V$[V]を、(b)のベクトル図より求めます。
$(50×6)^2+(50×3)^2=(\displaystyle\frac{V}{\sqrt{3}})^2$
$V=\sqrt{3}×\sqrt{(50×6)^2+(50×3)^2}≒581$[V]
答え (4)
2012年(平成24年)問6
次の文章は、同期発電機の自己励磁現象に関する記述である。
同期発電機は励磁電流が零の場合でも残留磁気によってわずかな電圧を発生し、発電機に( ア )力率の負荷をかけると、その( ア )電流による電機子反作用は( イ )作用をするので、発電機の端子電圧は( ウ )する。端子電圧が( ウ )すれば負荷電流は更に( エ )する。このような現象を繰り返すと、発電機の端子電圧は( オ )負荷に流れる電流と負荷の端子電圧との関係を示す直線と発電機の無負荷飽和曲線との交点まで( ウ )する。このように無励磁の同期発電機に( ア )電流が流れ、電圧が( ウ )する現象を同期発電機の自己励磁という。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 進み | 増磁 | 低下 | 増加 | 容量性 |
| (2) | 進み | 減磁 | 低下 | 減少 | 誘導性 |
| (3) | 遅れ | 減磁 | 低下 | 減少 | 誘導性 |
| (4) | 遅れ | 増磁 | 上昇 | 増加 | 誘導性 |
| (5) | 進み | 増磁 | 上昇 | 増加 | 容量性 |
2012年(平成24年)問6 過去問解説
同期発電機は励磁電流が零の場合でも残留磁気によってわずかな電圧を発生し、発電機に( 進み )力率の負荷をかけると、その( 進み )電流による電機子反作用は( 増磁 )作用をするので、発電機の端子電圧は( 上昇 )する。端子電圧が( 上昇 )すれば負荷電流は更に( 増加 )する。このような現象を繰り返すと、発電機の端子電圧は( 容量性 )負荷に流れる電流と負荷の端子電圧との関係を示す直線と発電機の無負荷飽和曲線との交点まで( 上昇 )する。このように無励磁の同期発電機に( 進み )電流が流れ、電圧が( 上昇 )する現象を同期発電機の自己励磁という。
答え (5)
2014年(平成26年)問5
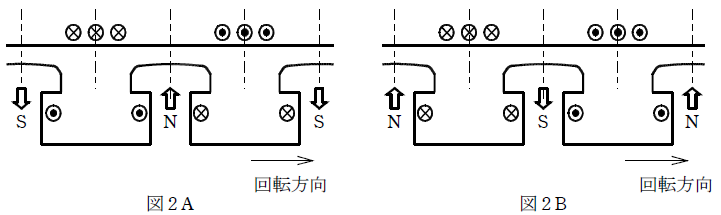
次の文章は、三相同期発電機の電機子反作用に関する記述である。
三相同期発電機の電機子巻線に電流が流れると、この電流によって電機子反作用が生じる。図1は、力率 1 の電機子電流が流れている場合の電機子反作用を説明する図である。電機子電流による磁束は、図の各磁極の( ア )側では界磁電流による磁束を減少させ、反対側では増加させる交差磁化作用を起こす。
次に遅れ力率 0 の電機子電流が流れた場合を考える。このときの磁極と電機子電流との関係は、図2( イ )となる。このとき、N及びS両磁極の磁束はいずれも( ウ )する。進み力率 0 の電機子電流のときには逆になる。
電機子反作用によるこれらの作用は、等価回路において電機子回路に直列に接続された( エ )として扱うことができる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 右 | A | 減少 | リアクタンス |
| (2) | 右 | B | 増加 | リアクタンス |
| (3) | 左 | A | 減少 | 抵抗 |
| (4) | 左 | B | 減少 | リアクタンス |
| (5) | 左 | A | 増加 | 抵抗 |
2014年(平成26年)問5 過去問解説
三相同期発電機の電機子巻線に電流が流れると、この電流によって電機子反作用が生じる。図1は、力率 1 の電機子電流が流れている場合の電機子反作用を説明する図である。電機子電流による磁束は、図の各磁極の( 右 )側では界磁電流による磁束を減少させ、反対側では増加させる交差磁化作用を起こす。
次に遅れ力率 0 の電機子電流が流れた場合を考える。このときの磁極と電機子電流との関係は、図2( A )となる。このとき、N及びS両磁極の磁束はいずれも( 減少 )する。進み力率 0 の電機子電流のときには逆になる。
電機子反作用によるこれらの作用は、等価回路において電機子回路に直列に接続された( リアクタンス )として扱うことができる。
答え (1)
2016年(平成28年)問15
定格出力 3300kV・A、定格電圧 6600V、定格力率 0.9(遅れ)の非突極形三相同期発電機があり、星形接続1相当たりの同期リアクタンスは 12.0Ω である。電機子の巻線抵抗及び磁気回路の飽和は無視できるものとして、次の(a)及び(b)の問に答えよ。
(a) 定格運転時における1相当たりの内部誘導起電力の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 3460 (2) 3810 (3) 6170 (4) 7090 (5) 8690
(b) 上記の発電機の励磁を定格状態に保ったまま運転し、星形結線1相当たりのインピーダンスが 13+j5Ω の平衡三相誘導性負荷を接続した。このときの発電機端子電圧の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 3810 (2) 4010 (3) 5990 (4) 6600 (5) 6950
2016年(平成28年)問15 過去問解説
(a) 一相等価回路図とベクトル図を示します。
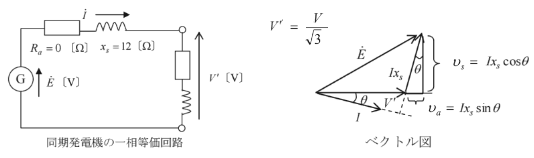
三相同期発電機の定格容量を $P$[V・A]、定格電圧を $V$[V]とすれば、定格電流 $I$[A]は、
$P=\sqrt{3}VI$
$I=\displaystyle\frac{P}{\sqrt{3}V}==\displaystyle\frac{3300×10^3}{\sqrt{3}×6600}≒288.7$[A]
電機子巻線抵抗を $R_a$[Ω]、同期リアクタンスを $x_s$[Ω]とすると、一相分抵抗の電圧降下 $v_a$[V]と一相分リアクタンスの電圧降下 $v_s$[V]は、
$v_a=IX_ssinθ=288.7×12×\sqrt{1-0.9^2}≒1510.5$[V]
$v_s=jIx_scosθ=j288.7×12×0.9≒j3118.0$[V]
定格電圧の相電圧は、
$\displaystyle\frac{V}{\sqrt{3}}=\displaystyle\frac{6600}{\sqrt{3}}≒3811$[V]
ベクトル図より、1相当たりの内部誘導起電力 $E$[V]は、
$E=\sqrt{(\displaystyle\frac{V}{\sqrt{3}}+v_a)^2+v_s^2}$
$=\sqrt{(3811+1510.5)^2+3118^2}≒6170$[V]
答え (3)
(b) 励磁は定格状態より、$E=6170$[V]の一定ですので、流れる電流を $I’$、回路の合成インピーダンスを $Z’$ 、発電機端子の相電圧 $V’$[V]とすると、
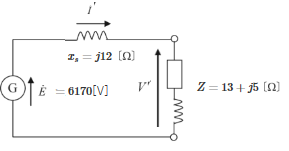
$Z’=x_s+Z=j12+13+j5=13+j17$
$I’=\displaystyle\frac{E}{Z’}=\displaystyle\frac{6170}{13+j17} $
$V’=I’Z’=\displaystyle\frac{6170}{13+j17}×(13+j5)=4015$
発電機端子の端子電圧 $V$[V]は、
$V=\sqrt{3}V’=\sqrt{3}×4015=6950$[V]
答え (5)
電験三種の機械科目に出題される「同期機」のページ
- 三相同期発電機の原理と構造
- 三相同期発電機の等価回路
- 三相同期発電機の特性
- 三相同期発電機の出力と並行運転
- 三相同期電動機の原理と特性
- 三相同期電動機の始動方法




