電力計の原理と二電力計法

第三種電気主任技術者（電験三種）試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「電力計の原理と二電力計法」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「電力計の原理と二電力計法」などの過去問題も解説しています。

電力計の原理と構造

電力を計算する式は、次の式で求めることができます。

直流電力：$P=VI$〔W〕
交流電力(瞬時値)：$P=VIcos θ$〔W〕

いずれにしても電圧と電流の積に比例します。したがって、電力を測定するためには、電圧と電流を同時に測定する必要があることがわかります。時間的に変化しない直流であれば、一つの計器で電圧と電流を別々に測定して、その積を計算することも可能ですが、時間的に変化する交流では、電圧と電流の位相関係が電力に影響を与えますので、電力計では同時に計測して各瞬間の電力を計算し、その平均値を求めますから、電圧と電流を同時に連続的に測定することが必要です。

図は、電流力計形電力計の構造を示しています。この計器では、固定コイルに負荷に流れる電流を通し、磁界を発生させます。この磁界の中にある可動コイル(指針と一緒に動くコイル)には、電源の電圧を加えて、電圧に比例する電流を流し、磁界を発生させます。この二つの磁界により指針が動くのですが、指針が振れる幅は電圧と電流の積に比例しますので、電力を測定できます。

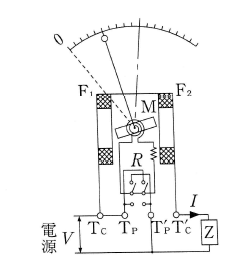
三相電力の測定（二電力計法）

三相交流回路における電力の測定は、平衡回路と不平衡回路で異なります。次の図は単相電力計を使って平衡三相回路の電力測定法です。スイッチを①側にして測定した値と②側に切り替えて測定した値の絶対値を加えて電力を求めます。絶対値を加えるという意味は、力率によって① もしくは②のいずれかが負の値(指針の逆振れ)になることがあるからです。

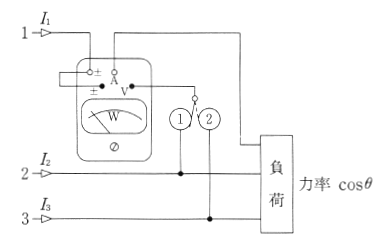
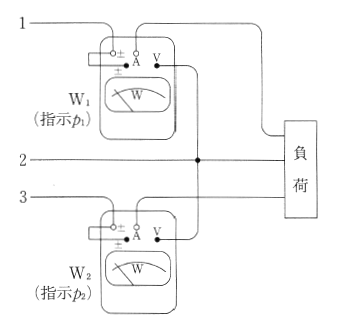
次の図は単相電力計2台を使って測定する方法で二電力計法といいます。この方法では、不平衡の三相交流回路でも電力を測定することが可能です。この方法でも、二つの電力計の指示値の絶対値を加えて電力を求めます。

　　

電験三種－理論の過去問解説：電力計の原理と二電力計法

(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。

2001年（平成13年）問13【電験理論の過去問題】

図は、単相交流 6,600[V]の電源に接続されている負荷の電力及び力率を発信装置付電力計及び電流計を用いて計測する回路である。この場合、次の(a)及び(b)に答えよ。

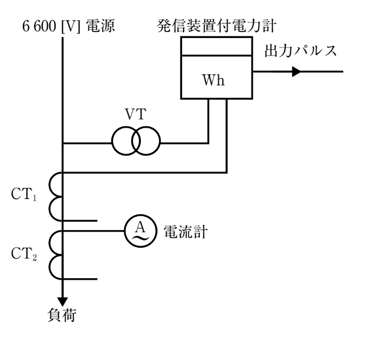
(a) 計器用変圧器VT及びCT₁の二次側に接続した電力量計の発信装置の出力パルスを、負荷が安定している 10分間測定したところ、そのパルス数は 130 であった。この負荷の1時間当たりの消費電力量 [kWh] の値として、正しいのは次のうちどれか。
ただし、この電力量計の発信装置の1[kWh]当たりの出力パルス数は 4,000 である。また、VT及びCT₁の一次定格/二次定格は、それぞれ 6,600V/110V 及び 100/5A である。

(1) 202　(2) 234　(3) 245　(4) 278　(5) 300

(b) この負荷に流れる電流を変流器CT₂の二次側に接続した電流計で測ったところ、電流計は 2.0 [A] を示した。この負荷の力率 [%] の値として正しいのは次のうちどれか。
ただし、変流器CT₂の一次側定格/二次側定格は、100/5A である。

(1) 76　(2) 82　(3) 85　(4) 89　(5) 92

2003年（平成15年）問13【電験理論の過去問題】

図のように、線間電圧 200 [V] の対称三相交流電流電源から三相平衡負荷に供給する電力を二電力計法で測定する。2台の電力計W₁及びW₂を正しく接続したところ、電力計W₂の指示が逆振れを起こした。
電力計W₂の電圧端子の極性を反転して接続した後、2台の電力計の指示値は、電力計W₁が 490 [W] 、電力計W₂が 25 [W] であった。このときの対称三相電源が三相平衡負荷に供給する電力 [W] の値として、正しいのはどれか。
ただし、三相交流電源の相回転は、a、b、cの順とし、電力計の電力損失は無視できるものとする。

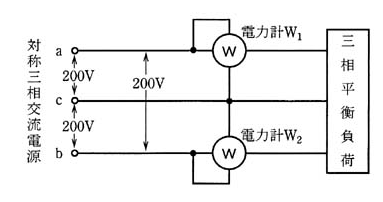
(1) 25　(2) 258　(3) 465　(4) 490　(5) 515

2011年（平成23年）問17 【電験理論の過去問題】

電力計について、次の(a)及び(b)の問に答えよ。

(a) 次の文章は電力計の原理に関する記述である。
図1に示す電力計は、固定コイルF1、F2に流れる負荷電流 $\dot{I}$ [A] による磁界の強さと、可動コイルMに流れる電流 $\dot{I}_M$ [A] の積に比例したトルクが可動コイルに生じる。したがって、指針の振れ角θは（　ア　）に比例する。
このような形の計器は、一般に（　イ　）計器と言われ、（　ウ　）の測定に使用される。
負荷$\dot{Z}$[Ω]が誘導性の場合、電圧$\dot{V}$ [V] のベクトルを基準に負荷電流 $\dot{I}$ [A] のベクトルを描くと、図2に示すベクトル①、②、③のうち（　エ　）のように表わされる。ただし、$φ$ [rad] は位相角である。
上記の記述中の空白個所(ア)，(イ)，(ウ)及び(エ)に当てはまる組み合わせとして、正しいものを次の(1)～(5)のうちから一つ選べ。

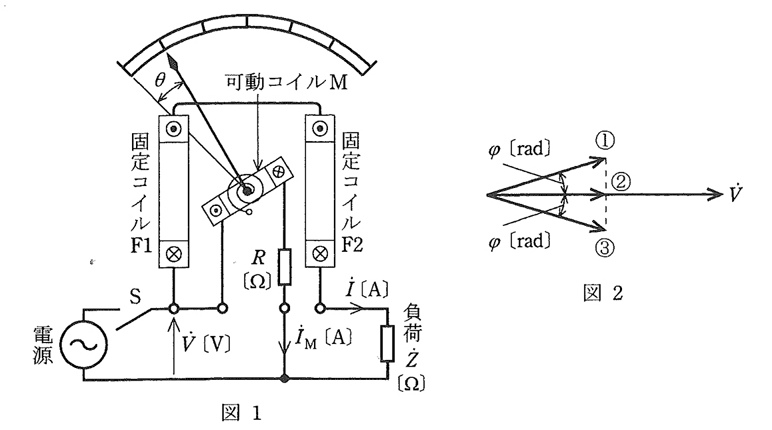
	（ア）	（イ）	（ウ）	（エ）
（1）	負荷電力	電流力計形	交　流	③
（２）	電力量	可動コイル形	直　流	②
（３）	負荷電力	誘導形	交流直流両方	①
（４）	電力量	可動コイル形	交流直流両方	②
（５）	負荷電力	電流力計形	交流直流両方	③

(b) 次の文章は、図1で示した単相電力計を 2 個使用し、三相電力を測定する 2 電力計法の理論に関する記述である。
図3のように、誘導性負荷 $\dot{Z}$ を 3 個接続した平衡三利囲負荷回路に対称三相交流電源が接続されている。ここで、線間電圧を $\dot{V}_{ab}$ [V]、$\dot{V}_{bc}$ [V]、$\dot{V}_{ca}$ [V]、負荷の相電圧を $\dot{V}_{a}$ [V]、$\dot{V}_{b}$ [V]、$\dot{V}_{c}$ [V]、線電流を $\dot{I}_{a}$ [A]、$\dot{I}_{b}$ [A]、$\dot{I}_{c}$ [A] で示す。

この回路で、図のように単相電力計 $W_1$ と $W_2$ を接続すれば、平衡三相負荷の電力が、2個の単相電力計の指示の和として求めることができる。
単相電力計 $W_1$ の電圧コイルに加わる電圧 $\dot{V}_{ac}$ は、図４のベクトル図から $\dot{V}_{ac}= \dot{V}_{a}- \dot{V}_{c}$ となる。また、単相電力計 $W_2$ の電圧コイルに加わる電圧 $\dot{V}_{bc}$ は、$\dot{V}_{bc}=$ （　オ　）となる。

それぞれの電流コイルに流れる電流 $\dot{I}_{a}$ 、$\dot{I}_{b}$ と電圧の関係は図４のようになる。図４における$φ$[rad] は相電圧と線電流の位相角である。
線間電圧の大きさを $V_{ab}=V_{bc}=V_{ca}=V$［V］、線電流の大きさを $I_a=I_b=I_c=I$［A］とおくと、単相電力計 $W_1$ 及び $W_2$ の指示をそれぞれ $P_1$［W］、$P_2$［W］とすれば、

$P_1=V_{ac}I_acos( (　カ　）)$ [W]
$P_2=V_{bc}I_bcos( (　キ　）)$ [W]

したがって、$P_1$と$P_2$の和$P$［W］は、

$P=P_1+P_2=VI(（　ク　）)cosφ=\sqrt{3}VIcosφ$ [W]

となるので、2 個の単相電力計の指示の和は三相電力に等しくなる。

上記の記述中の空白個所(オ)，(カ)，(キ)及び(ク)に当てはまる組み合わせとして、正しいものを次の(1)～(5)のうちから一つ選べ。

	(オ)	(カ）	(キ）	(ク）
（１）	$\dot{V}_b-\dot{V}_c$	$\displaystyle\frac{π}{6}-φ$	$\displaystyle\frac{π}{6}+φ$	$2cos\displaystyle\frac{π}{6}$
（２）	$\dot{V}_c-\dot{V}_b$	$ φ – \displaystyle\frac {π}{6}$	$ φ + \displaystyle\frac {π}{6}$	$2cos\displaystyle\frac{π}{6}$
（３）	$\dot{V}_b-\dot{V}_c$	$\displaystyle\frac{π}{6}-φ$	$\displaystyle\frac{π}{6}+φ$	$2cos\displaystyle\frac{π}{3}$
（４）	$\dot{V}_b-\dot{V}_c$	$\displaystyle\frac{π}{3}-φ$	$\displaystyle\frac{π}{3}+φ$	$2cos\displaystyle\frac{π}{6}$
（５）	$\dot{V}_c-\dot{V}_b$	$\displaystyle\frac{π}{3}-φ$	$\displaystyle\frac{π}{3}+φ$	$2cos\displaystyle\frac{π}{3}$