電験三種の法規で出題される発電電力と系統連系について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の試験で、実際に出題された過去問題も解説しています。
水力発電所の出力
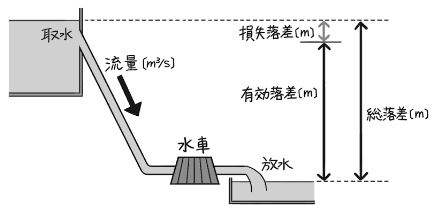
水力発電所の出力は、「落差」と「流量」に関係しています。落差は、水車が動力として利用する水位の差のことで、取水口から放水口までの水位差を「総落差」、総落差から損失分を差し引いた落差を「有効落差」といいます。
有効落差(H)=総落差(HG)-損失落差(h1)
水力発電所の理論出力
水力発電所の理論出力 P0[kW]は、使用水量を Q[m3/s]、有効落差を H[m]とすると、次の式で求めることができます。
P0=9.8QH[kW]
水車出力
水力発電所の理論出力から水車で生じる摩擦などの損失を差し引いた出力を水車出力 Pw[kW]といいます。水車効率を ηw[%](ηの読み:イータ)とすると、次の式で求めることができます。
Pw=9.8QHηw[kW]
発電機出力
発電機は水車と直結されていますので、水車の出力は発電機の入力となります。発電機効率を ηG[%]とすると、発電機出力 PG[kW]は次の式で求めることができます。
PG=9.8QHηwηG[kW]
尚、η=ηwηG を総合効率といいます。
揚水発電所
揚水発電所は夜間の軽負荷時や豊水期などに発生する余剰電力を利用して、ポンプで貯水池に揚水し、ピーク時に貯水を発電に利用する発電所です。
余剰電力を位置エネルギーに変換して蓄えておき、必要に応じて再び電気エネルギーに変換する蓄電設備の一種として考えることができます。
揚水発電所の総合効率
揚水のための必要な電力(揚水電力)に対する発電時の出力(発電機出力)の割合を求めると、揚水発電の総合効率が算出できます。
$総合効率=\displaystyle \frac{ 発電機出力P_G }{ 揚水電力P_P}×100$[%]
電験三種-法規(施設管理)過去問題
1998年(平成10年)問12
自家用水力発電所を有して一般電気事業者(電力会社)と常時系統連系している工場があり、この1日の負荷持続曲線は、次の式及び図で表される。
P=15000-400t
ただし、P は負荷[kW]、t は時間[h]とする。
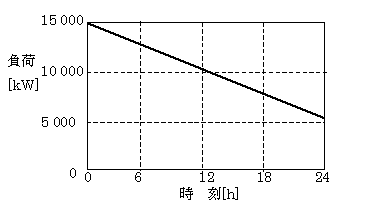
工場の需要電力に対し、発電電力に余剰を生ずるときは電力系統に送電している。いま、この水力発電所のある日の発生電力が 10000[kW]であったとすると、その日の電力系統への送電電力量[kWh]の値として、正しいのは次のうちどれか。
(1) 25000 (2) 25500 (3) 26000 (4) 26500 (5) 27000
1998年(平成10年)問12 過去問解説
送電開始時刻を求めます。P=15000-400t より、負荷が 10000[kW]になる時刻が送電開始時刻ですので、
10000=15000-400t
t=12.5[h]
したがって、送電時間は 24-12.5=11.5[h]になります。
t=24[h]の負荷電力は、
P=15000-400×24=5400[kW]
ですので、24時の送電電力は
10000-5400=4600[kW]
になります。送電電力量は図のAの面積に相当します。したがって、
$送電電力量=\displaystyle \frac{ 11.5×4600 }{ 2 }=26500$[kWh]
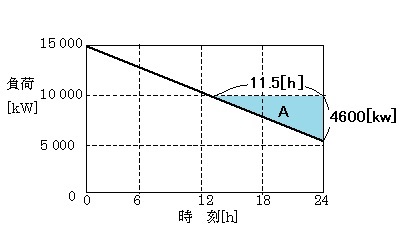
答え (4)
2003年(平成15年)問13
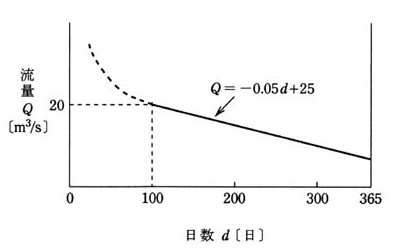
最大使用水量 15[m3/s]、有効落差 20[m]の流込式水力発電所がある。この発電所が利用している河川の流量 Q が図のような年間流況曲線(日数 d が 100日以上の部分は、Q=-0.05d+25[m3/s]で表される。)であるとき、次の(a)及び(b)に答よ。
ただし、水車及び発電機の効率はそれぞれ 90[%]及び 95[%]で、流量によって変化しないものとする。
(a) この発電所で年間に溢(いつ)水が発生する日数の合計として、最も近いのは次のうちどれか。
ただし、溢水とは河川流量を発電に利用しないで無効に放流することをいう。
(1) 180 (2) 190 (3) 200 (4) 210 (5) 220
(b) この発電所の年間可能発電電力量[GW・h]の値として、最も近いのは次のうちどれか。
(1) 19.3 (2) 20.3 (3) 21.4 (4) 22.0 (5) 22.5
2003年(平成15年)問13 過去問解説
(a) Q=-0.05d+25 の式に、最大使用水量 15[m3/s]を Q に代入して解くと、
15=-0.05d+25
d=200[日]
答え (3)
(b) (a)より0から 200日は、発電をするにあたって、最大使用水量 15[m3/s]を使います。発電電力量を $W_1$[GW・h]とすると、
$\begin{eqnarray} W_1 &=& 9.8QHη_tη_gh \\&=& 9.8×15×20×0.9×0.95×24×200 \\&=& 12.06[GW・h]\end{eqnarray}$
200日目の最大使用水量は 15[m3/s]で、365日目の最大使用水量は、$Q=-0.05d+25$より、
$Q_{365}=-0.05×365+25=6.75$[m3/s]
200日目から365日目までの平均使用水量 $Q_H$[m3/s]は、
$Q_H=\displaystyle \frac{ 15+6.75 }{ 2 }=10.875$[m3/s]
200日から365日までの、発電電力量を $W_2$[GW・h]とすると、
$\begin{eqnarray} W_2 &=& 9.8QHη_tη_gh \\&=& 9.8×10.875×20×0.9×0.95×24×(365-200) \\&=& 7.2[GW・h]\end{eqnarray}$
年間可能発電電力量[GW・h]は、
$年間可能発電電力量=W_1+W_2=19.3$[GW・h]
答え (1)
2005年(平成17年)問13
有効落差 80[m]の調整池式水力発電所がある。河川の流量が 12[m3/s]で一定で、図のように 1日のうち 18時間は発電せずに全流量を貯水し、6時間だけ自流分に加え貯水分を全量消費して発電を行うものとするとき、次の(a)及び(b)に答えよ。
ただし、水車及び発電機の総合効率は 85[%]、運転中の有効落差は一定とし、溢水はないものとする。
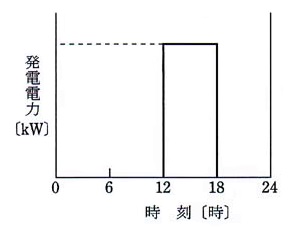
(a) 1日当たりの総流入量[m3]の値として、最も近いのは次のうちどれか。
(1) 288×103 (2) 780×103 (3) 860×103 (4) 1040×103 (5) 1730×103
(b) 発電電力[kW]の値として、最も近いのは次のうちどれか。
(1) 20000 (2) 27000 (3) 28000 (4) 32000 (5) 37000
2005年(平成17年)問13 過去問解説
(a) 流量に時間(60×60×24)をかければ、総流入量を求めることができます。 1日当たりの総流入量 $V$[m3]は、
$V =12×60×60×24 = 1040×10^3[m^3]$
答え (4)
(b) 24時間分を6時間で発電するので流量を4(=24/6)倍して、発電電力の公式に数値を代入します。発電電力 $P$[kW]は、
$\begin{eqnarray}P&=&9.8QHη\\\\&=&9.8×(12×4)×80×0.85\\\\&≒&32 000[kW]\end{eqnarray}$
答え (4)
2008年(平成20年)問13
自家用水力発電所を有し、電力系統(電力会社)と常時系統連系(逆潮流ができるものとする。)している工場がある。この工場のある1日の負荷は図のように変化した。
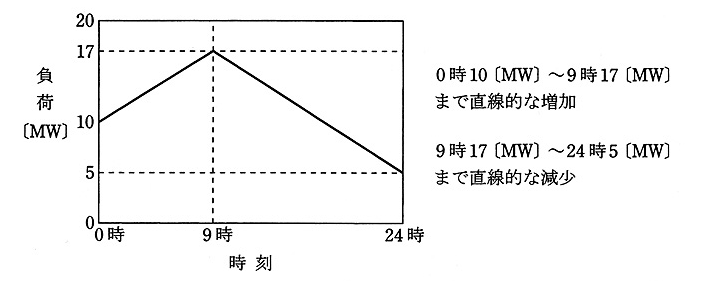
この日の水力発電所の出力は10[MW]一定であった。次の(a)及び(b)に答えよ。
ただし、水力発電所の所内電力は無視するものとする。
(a) この日の電力系統からの受電電力量[MW・h]の値として、最も近いのは次のうちどれか。
(1) 45.4 (2) 58.6 (3) 62.1 (4) 65.6 (5) 70.7
(b) この日の受電電力量[MW・h](A)に対して送電電力量[MW・h](B)の比率(B/A)として、最も近いのは次のうちどれか。
(1) 0.20 (2) 0.22 (3) 0.23 (4) 0.25 (5) 0.28
2008年(平成20年)問13 過去問解説
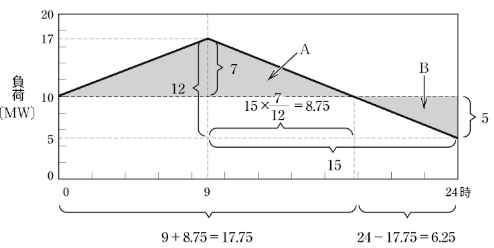
(a) 受電電力量は、図のAの面積に相当します。
Aの面積:$\displaystyle \frac{ 17.75×7 }{ 2 }≒62.1$[MW・h]
答え (3)
(b) 送電電力量は、図のBの面積に相当します。
Aの面積:$\displaystyle \frac{ 6.25×5 }{ 2 }≒15.6$[MW・h]
求める比率は、
$\displaystyle \frac{ B }{ A }=\displaystyle \frac{ 15.6 }{ 62.1 }≒0.25$
答え (4)
2012年(平成24年)問13
発電所の最大出力が 40000[kW]で最大使用水量が 20[m3/s]、有効容量 360000[m3]の調整池を有する水力発電所がある。河川流量が 10[m3/s]一定である時期に、河川の全流量を発電に利用して図のような発電を毎日行った。毎朝満水になる 8 時から発電を開始し、調整池の有効水量の水を使いきる $x$ 時まで発電を行い、その後は発電を停止して翌日に備えて貯水のみをする運転パターンである。次の (a) 及び (b) の問に答えよ。
(a) 運転を終了する時刻 x として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 19 時 (2) 20 時 (3) 21 時 (4) 22 時 (5) 23 時
(b) 図に示す出力 $P$[kW]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 20000 (2) 22000 (3) 24000 (4) 26000 (5) 28000
2012年(平成24年)問13 過去問解説
(a) 有効容量 360000[m3]の調整池に貯水を開始する時刻 $x$ を求めます。
(24-x) [時]×10[m3/s]×3600[s]+(8-0)[時]×10[m3/s]3600[s]=360000[m3]
$X=22$[時]
答え (4)
(b) 河川流量が 10[m3/s]一定なので、一日の全使用水量を $W$[m3]とすると
$W=10×24×3600=864000$[m3]
発電所出力と流量は比例しますので、
${4×\frac{ P }{ 40000 }×20+1×\frac{16000 }{ 40000 }×20+(22-13)×20}×3600=864000$
$(\frac{ P }{ 500}+8+180)=240$
$ P=26000$[kW]
答え (4)
2013年(平成25年)問12
出力 600[kW]の太陽電池発電所を設置したショッピングセンターがある。ある日の太陽電池発電所の発電の状況とこのショッピングセンターにおける電力消費は図に示すとおりであった。すなわち、発電所の出力は朝の 6 時から 12 時まで直線的に増大し、その後は夕方 18 時まで直線的に下降した。また、消費電力は深夜 0 時から朝の 10 時までは 100[kW]、 10 時から 17 時までは 300[kW]、17 時から 21 時までは 400[kW]、21 時から 24 時は 100[kW]であった。
このショッピングセンターは自然エネルギーの活用を推進しており太陽電池発電所の発電電力は自家消費しているが、その発電電力が消費電力を上回って余剰を生じたときは電力系統に送電している。次の (a) 及び (b) の問に答えよ。
(a) この日、太陽電池発電所から電力系統に送電した電力量[kW・h]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 900 (2) 1300 (3) 1500 (4) 2200 (5) 3600
(b)この日、ショッピングセンターで消費した電力量に対して太陽電池発電所が発電した電力量により自給した比率 [%] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 35 (2) 38 (3) 46 (4) 52 (5) 58
2013年(平成25年)問12 過去問解説
(a) 送電電力量は、図のAとBの面積に相当します。まず、発電電力と消費電力が交わる時間を考えます。
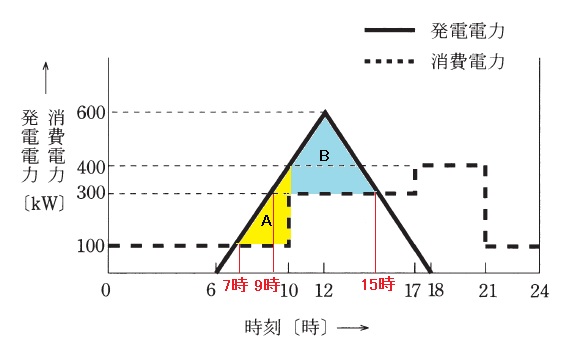
発電電力のグラフ
・6時~12時 傾き 100 (1時間ごとに100[kW]上がり)
・12時~18時 傾き-100 (1時間ごとに100[kW]下がり)
消費電力と発電電力が交わる時刻
・100[kW]ライン 7時
・100[kW]ライン 9時と15時
送電した電力量をA,Bの面積として計算します。
・Aの面積
(400-100)[kW]×3[h]×1/2=450[kW・h]
・Bの面積
(600-300)[kW]×6[h]×1/2 – (400-300[kW]×1[h]×1/2=850[kW・h]
したがって、A,Bの合計は、1300[kW・h]
答え (2)
(b) ショッピングセンターで消費された電力量を $W_1$[kW・h]とすると、
0時から10時:100[kW]×10[h]
10時から17時:300[kW]×7[h]
17時から21時:400[kW]×4[h]
21時から24時:100[kW]×3[h]
$W_1=1000+2100+1600+300=5000[kW・h]$
太陽電池発電所の発電電力量を $W_2$[kW ・ h]とすると、
$W_2=600×(18-6)×\displaystyle \frac{ 1 }{ 2 }=3600[kW・h]$
この 3600[kW ・ h]のうち 1300[kW ・ h]hは、送電した電力量です。自給した電力量を $W_2’$[kW・h]とすると、
$W_2’=3600-1300=2300[kW・h]$
自給した比率$α$は、
$α=\displaystyle \frac{ W_2’ }{ W_1 }×100=\displaystyle \frac{ 2300}{ 5000 }×100=46[%]$
答え (3)
2017年(平成29年)問13
自家用水力発電所をもつ工場があり、電力系統と常時系統連系している。
ここでは、自家用水力発電所の発電電力は工場内において消費させ、同電力が工場の消費電力よりも大きくなり余剰が発生した場合、その余剰分は電力系統に逆潮流(送電)させる運用をしている。
この工場のある日(0時~24時)の消費電力と自家用水力発電所の発電電力はそれぞれ図1及び図2のように推移した。次の(a)及び(b)の問に答えよ。
なお、自家用水力発電所の所内電力は無視できるものとする。
(a) この日の電力系統への送電電力量の値[MW・h]と電力系統からの受電電力量の値[MW・h]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
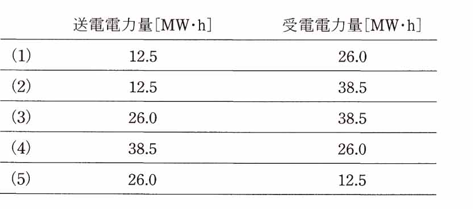
(b) この日、自家用水力発電所で発電した電力量のうち、工場内で消費された電力量の比率[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)18.3 (2)32.5 (3)81.7 (4)87.6 (5)93.2
2017年(平成29年)問13 過去問解説
(a) 設問の図1と2を重ね合わせます。
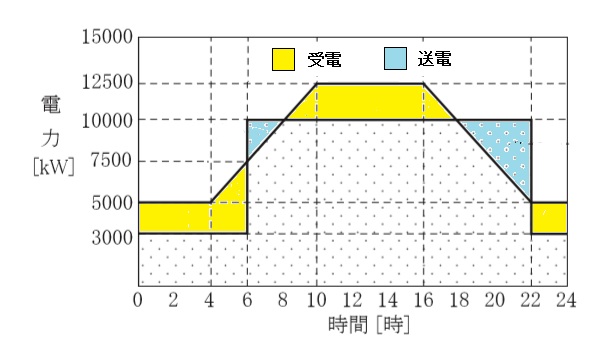
黄色部分は発電だけでは足りないので、受電が必要です。受電電力量は、図の黄色部分の面積に相当します。青部分は余分に発電しており、送電可能な電力です。送電電力量は、図の青色部分の面積に相当します。
計算すると、送電電力量は12.5[MW・h] 、受電電力量は38.5[MW・h]になります。
答え (2)
(b) 自家用水力発電所で発電した電力量の合計は、設問の図2の網掛け部分の面積に相当します。
計算すると、自家用水力発電所で発電した電力量は184[MW・h]になります。このうち、工場内で消費された電力量は、送電電力量は12.5[MW・h]を差し引いた電力量ですので、171.5[MW・h]になります。
工場内で消費された電力量の比率[%]は、
$α=\displaystyle \frac{ 171.5 }{ 184 }×100=93.2[%]$
答え (5)