照明工学の計算

このページでは、照明工学の計算について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された照明工学の計算の過去問題の解き方も解説しています。

光に関する量

光に関するいろいろな量について説明します。照明計算ではこれらが計算の基礎となります。

• 光束：光源から出る光の量（単位：ルーメン［lm］）
• 光度：ある方向へ向かう光の強さ（単位：カンデラ［cd］）
• 照度：光に照らされる面の明るさ（単位：ルクス［lx］）
• 輝度：発光面の輝きの度合い（単位：カンデラ毎平方メートル［cd/m²］）
• 光束発散度：発光面が発散する光束の度合い（単位：ルーメン毎平方メートル［lm/m²］）

光束と光度

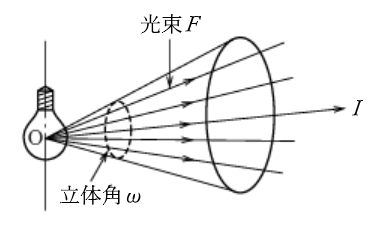
光源が発する目に見える光の量を光束 $ϕ$ といいます。ランプから出る光の量は光束で表し、単位はルーメン［lm］で表します。また、光源がある方向に向けて発する光の強さを光度 $I$ といい、単位はカンデラ［cd］で表します。光束と光度には、次のような関係があります。

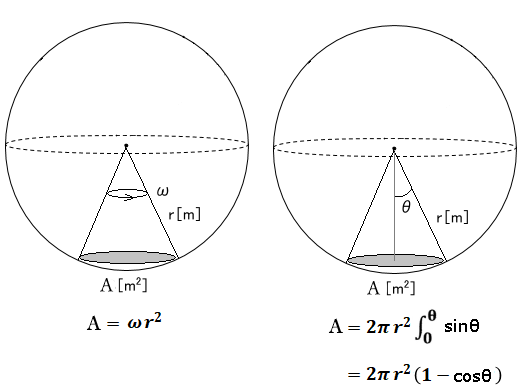
立体角とはある点から放射状に延びる空間の広がりを表すものです。立体角の単位はステラジアン［sr］で表します。下図のように点Ｏを中心とする半径 $r$［m］の球面から面積 $S$［m²］を切り取ったとき、点Ｏから面積Sに広がる空間の立体角 $ω$ は次の式で表すことができます。

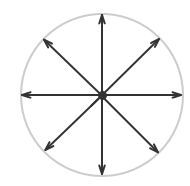
なお、光源から放射される全光束 $ϕ_o$ ［lm］の分布が均等（一様）な場合、あらゆる方向に対する光度 $I$［cd］は同じになります。

$I=\displaystyle\frac{ϕ_o$}{4π}$［cd］

このようなあらゆる方向の光度I［cd］が同じでる点光源を均等点光源といいます。

照度：面の明るさ

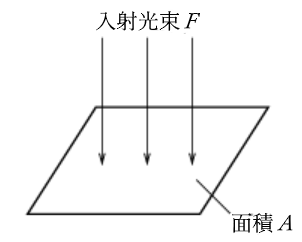
光源自体の明るさは光束で表せますが、光源に照らされた面の明るさのことを照度 $E$ といいます。照度は照らされた面の単位面積(1m²)に受ける光束の量のことで、単位はルクス［lx］で表します。

輝度：光源のまぶしさ

光源をある方向から見たときのまぶしさや輝きの度合いを輝度 $L$ といいます。輝度は光源の単位面積(1m²)から出る光度のことで、単位はカンデラ毎平方メートル［cd/m²］で表します。

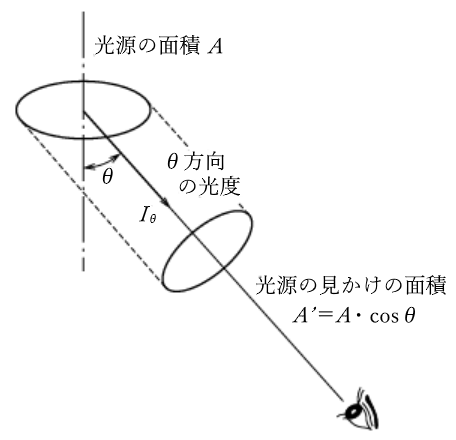
まぶしさの度合いは光源を見る角度によって異なる場合があります。そのため輝度の計算では光源の実際の面積ではなく、光源をある方向から見たときの見かけの面積が使われます。

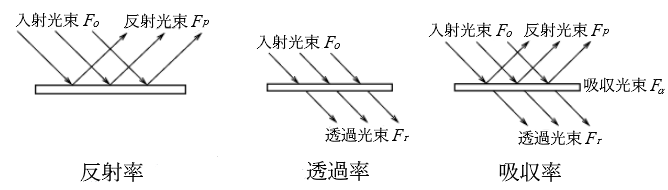
反射率・透過率・吸収率

ある物体への入射光束に対する反射光束の比を反射率 $ρ$ といいます。ある面に入射する光束を $ϕ_0$［lm］ 、この面より反射する光束を $ϕ_ρ$［lm］とすると、反射率 $ρ$ は、

$ρ=\displaystyle\frac{ϕ_ρ}{ϕ_0}$

半透明な物体に光が当たった場合、その物体への入射光束に対する透過光束の比を透過率 $τ$ といいます。ある面に反射する光束を $ϕ_0$［lm］ 、この物体を透過する光束を $ϕτ$［lm］ とすると、透過率 $τ$ は、

$τ=\displaystyle\frac{ϕτ}{ϕ_o}$

ある物体への入射光束に対する、その物体内で吸収された光束の比を吸収率 $α$ といいます。ある面に入射する光束を $ϕ_0$［lm］ 、この物体内で吸収された光束を $ϕ_α$［lm］とすると、吸収率 $α$ は、

$α=\displaystyle\frac{ϕ_α}{ϕ_o}$

物体に入射した光束のうち、反射も透過もしない分が吸収されますので、次の関係が成り立ちます。

$ϕ_α=ϕ_0–ϕ_ρ–ϕτ$
$ρ+τ+α=1$

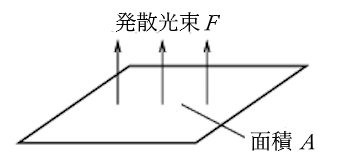
光束発散度

単位面積(1m²)の発光面から発散する光束の量を光束発散度 $M$ といいます。光束発散度は、人の眼に感じられる明るさを表す度合いです。単位はルーメン毎平方メートル［lm/m²］で表します。

光束発散度は反射面、透過面からも定義ですることができます。反射率を $ρ$、透過率を $τ$、その面の照度を $E$［lx］とすると、反射面，透過面に対する光束発散度 $M_ρ$，$Mτ$ は、

$M_ρ=ρ⋅E$
$Mτ=τ⋅E$

さらに、均等拡散面の場合は、光束発散度 $M$［lm/m²］と輝度 $L$［cd/m²］との間には次の関係があります。

$M=π⋅L$

点光源による照度計算

位置だけが定まり大きさを持たない光源を点光源といいます。点光源に対しては、照度の計算に距離の逆2乗の法則が適用できます。実際には点光源というものは存在しないので正確な計算は不可能ですが、光源の大きさの5倍以上の距離を隔てた被照点において適用するなら、誤差は1［%］以下が期待でき、実用上十分であるとされています。

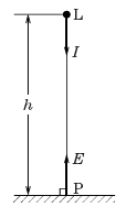
距離の逆2乗の法則

点光源 L の方向と垂直な面の照度を法線照度 $E$ といいます。光源から光を直角に受ける平面上のP点線の法線照度 $E$［lx］は、その方向の光度 $I$［cd］に比例し、点光源 L と P点との距離 $h$［m］の2乗に逆比例します。これを距離の逆2乗の法則といいます。

入射角の余弦法則

ある面上の照度は、光の入射角（入射光と面の法線とのなす角）の余弦（コサイン）に比例します。被照面Gに対する法線PNが光の方向LPと $θ$ の角度を持つとき、被照面G上P点の照度 $E$［lx］は、

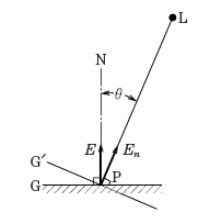
水平面照度と鉛直面照度

机上面や道路面など水平な面の照度を水平面照度 $E_h$ といい、黒板面や壁面など鉛直な面の照度を鉛直面照度 $E_v$ といいます。水平面照度 $E_h$［lx］と鉛直面照度 $E_v$［lx］は、距離の逆2乗の法則と入射角の余弦法則から求めることができます。

照明率と保守率

光源から出た光束に対する、作業面上の光束の割合を照明率 $U$ といいます。照明率は、光束法による照明設計計算に用いられます。光源から出た光は照明器具内で反射・吸収・透過されて器具外へ出ます。外へ出た光は直接作業面を照射する光と天井・壁・床で反射して作業面に達する光があります。したがって、照明率は照明器具の配光、器具効率、室指数（室の間口、奥行、天井高さで決まる）、室の反射率により定まってきます。

光源の光束を $ϕ_0$［lm］、照明器具から出る光束を $ϕ_l$［lm］、作業面上への入射光束を $ϕ_w$［lm］とすれば、照明率Uは、次の式で表わすことができます。

$U=\displaystyle\frac{ϕ_w}{ϕ_0}=\displaystyle\frac{ϕ_w}{ϕ_l}×\displaystyle\frac{ϕ_l}{ϕ_0}=U_0×η$
$U_0=\displaystyle\frac{ϕ_w}{ϕ_l}$ ：固有照明率
$η=\displaystyle\frac{ϕ_l}{ϕ_0}$：器具効率

照明器具を一定期間使用した後、ランプの光束の減少や器具の汚れなどにより低下した照度と初期照度の比を保守率といいます。保守率は、一般照明の場合0.7程度です。全般照明の照度計算を行うとき保守率が用いられます。必要な照明器具台数 $N$ とすれば、平均照度 $E$［lx］は次の式で表わすことができます。

$E=\displaystyle\frac{FNMU}{A}$
$E$：平均照度［lx］、$A$：室面積［m²］、$F$：照明器具1台当たりの光束［lm］、$N$：照明器具台数 、$U$：照明率（全光束のうちの有効光束の割合）、$M$：保守率

　　

電験三種－機械（照明）過去問

1997年（平成9年）問6

完全拡散性の直管蛍光ランプがあり、管の直径が 38［mm］、管の発光部分の長さが 600［mm］、その軸と直角方向の光度は 114［cd］で一定である。この蛍光ランプの輝度［cd/m²］として、正しいのは次のうちどれか。

(1) 795　(2) 1590　(3) 2500　(4) 2600　(5) 5000

1997年（平成9年）問6　過去問解説

直管蛍光ランプの直径を $D$［m］、長さを $L$［m］とすると、光源の垂直方向のみかけ面積（垂直投影面積） $S’$［m²］は、

$S’=D×L×cos0=D×L$［m²］

となります。ランプの光度を $I$［cd］とすると、輝度 $L$［cd/m²］は、

$L=\displaystyle\frac{I}{S’}=\displaystyle\frac{114}{38×10^{-3}×600×10^{-3}}=5000$［cd/m²］

答え (5)

1999年（平成11年）問13

図に示すような幅 6［m］、奥行き 8［m］の長方形の駐車場の四隅に柱を立て、各柱の地上から 5［m］の頂点に全光束 5000［lm］の水銀ランプを設置した。駐車場の中心Oの水平面照度［lx］の値として、正しいのは次のうちどれか。ただし、各水銀ランプは均等点光源とする。

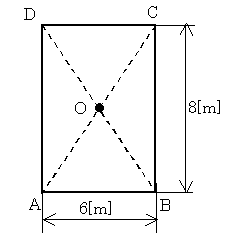
(1) 5.6　(2) 22.5　(3) 31.8　(4) 141　(5) 283

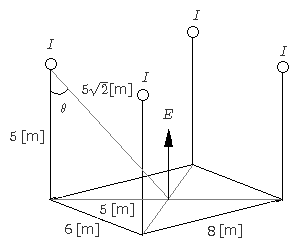
1999年（平成11年）問13　過去問解説

$AO=\sqrt{3^2+4^2}=5$［m］ですので、各水銀ランプからO点までの距離 $p$［m］は、

$p=\sqrt{5^2+5^2}=5\sqrt{2}$［m］

水銀ランプ1個の全光束を $ϕ_o$［lm］とすると、水銀ランプは均等点光源ですので、1個当たりの光度 $I$［cd］は、

$I=\displaystyle\frac{ϕ_o}{4π}=\displaystyle\frac{5000}{4π}≒398$［cd］

Ａ点の光源による水平面照度を $E_h$［lx］とすると、

$E_h=\displaystyle\frac{I⋅cosθ}{p^2}=\displaystyle\frac{398⋅\frac{5}{5\sqrt{2}}}{(\sqrt{5^2+5^2})^2}≒5.63$［lx］

同じように、水平面照度を $E_h$［lx］が合計4つの水銀ランプがありますので、

$E=5.63×4＝22.5$［lx］

答え (2)

2000年（平成12年）問6

間口 4［m］、奥行き 6［m］の室の天井に 40ワット蛍光ランプ２灯用照明器具(下面開放形)を４基取り付けた。床面の平均照度［lx］の値として、正しいのは次のうちどれか。
ただし、蛍光ランプの効率は 75[lm/Ｗ]、保守率は 0.7、床面に対する照明率は 0.4とする。

(1) 140　(2) 200　(3) 280　(4) 400　(5) 570

2000年（平成12年）問6　過去問解説

室面積を $A$［m²］、照明器具1台当たりの光束を $F$［lm］、照明器具台数を $N$ 、照明率を $U$、保守率を $M$ とすると、平均照度 $E$［lx］は、

$E=\displaystyle\frac{FNMU}{A}=\displaystyle\frac{3000×8×0.4×0.7}{24}=280$

A=4［m］×6［m］=24［m²］
F=40［W］×75［lm/Ｗ］＝3000［lm］
N=2［灯］×4［基］=8

答え (3)

2002年（平成14年）問13

光束 5,000［lm］の均等放射光源がある。その全光束の 60［%］で面積 4［m²］の完全拡散性白色紙の片方の面(Ａ面)を一様に照射して、透過率 0.4(40%)その透過光により照明を行った。これについて、次の(a)及び(b)に答えよ。

(a) 透過して白色紙の他の面(Ｂ面)から出る面積 1［m²］当たりの光束(光束発散度)［lm/m²］の値として、正しいのは次のうちどれか。

(1) 150　(2) 300　(3) 500　(4) 750　(5) 1200

(b) 白色紙のＢ面の輝度［cd/m²］の値として、正しいのは次のうちどれか。

(1) 23.9　(2) 47.8　(3) 95.5　(4) 190　(5) 942

2002年（平成14年）問13　過去問解説

(a) 照度を $E$［lx］，光束を $ϕ$［lm］，面積を $S$［m²］，透過率を $τ$ とすると、透過面に対する光束発散度 $Mτ$ は、

$Mτ=τ⋅E=τ⋅\displaystyle\frac{ϕ}{S}=0.4×\displaystyle\frac{5000×0.6}{4}=300$［lm/m²］

答え (2)

(b) 輝度 $L$［cd/m²］は、

$Mτ=π⋅L$
$300=π⋅L$
$L≒95.5$［cd/m²］

答え (3)

2003年（平成15年）問10

床面積 20［m］×60［m］の工場に、定格電力 400［W］、総合効率 55［lm/W］の高圧水銀ランプ 20個と、定格電力 220［W］、総合効率 120[lm/W]の高圧ナトリウムランプ 25個を取り付ける設計をした。照明率を 0.60、保守率を 0.70としたときの床面の平均照度［lx］の値として、正しいのはつぎのうちどれか。
ただし、総合効率は安定器の損失を含むものとする。

(1) 154　(2) 231　(3) 385　(4) 786　(5) 1069

2003年（平成15年）問10　過去問解説

室面積を $A$［m²］、照明器具1台当たりの光束を $F$［lm］、照明器具台数を $N$ 、照明率を $U$、保守率を $M$ とすると、平均照度 $E$［lx］は、

$E=\displaystyle\frac{FNMU}{A}$

高圧水銀ランプの平均照度 $E_1$［lx］は、

$E_1=\displaystyle\frac{400×55×0.7×0.6×20}{20×60}=154$［lx］

高圧ナトリウムランプの平均照度 $E_2$［lx］は、

$E_2=\displaystyle\frac{220×120×0.7×0.6×25}{20×60}=231$［lx］

したがって、両器具の平均照度の合計は、

$E_1+E_2=154+231=385$［lx］

答え (3)

2006年（平成18年）問17

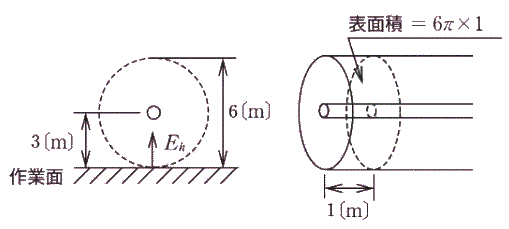
管径 36［mm］の完全拡散無限直線光源を床面上 3［m］の高さに床面と平行に配置した、光源からは単位長当たり 3,000［lm/m］の光束を一様に発散しているものとして、次の(a)及び(b)に答えよ。

(a) 直線光源の光束発散度 M［lm/m²］の値として、最も近いのは次のうちどれか。

(1) 4.2×10³　(2) 8.4×10³　(3) 26.5×10³　(4) 74.7×10³　(5) 83.3×10³

(b) 光源直下の床面の水平面照度 E_h［lx］の値として、最も近いのは次のうちどれか。

(1) 80　(2) 159　(3) 239　(4) 318　(5) 333

2006年（平成18年）問17　過去問解説

(a) 光束発散度 $M$［lm/m²］は、光源 1［m］の光束 $ϕ$［lm］を、光源 1［m］の表面積で割ったものですので、

M=\displaystyle\frac{3000}{36×10^{-3}×π×1}≒26.5×10^3$［lm/m²］

答え (3)

(b) 無限直線光源は、光源を中心とした円筒として考えます。円筒の長さが 1［m］当たりの光束を、円筒の長さ 1［m］当たりの表面積で割ります。

$E_h=\displaystyle\frac{3000}{3×2π×1}≒159$［lm］

答え (2)

2007年（平成19年）問11

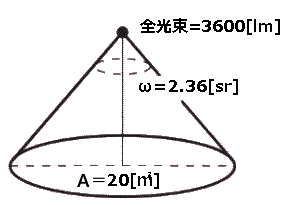
円形テーブルの中心点から真上に全光束 3600［lm］で均等放射する白熱電球を取り付けた。この円形テーブル面の平均照度［lx］の値として、最も近いのは次のうちどれか。
ただし、電球から円形テーブル面までの距離に比べ電球の大きさは無視できるものとし、電球から円形テーブル面を見た立体角は 2.36［sr］、円形テーブルの面積は 20［m²］とする。

(1) 14　(2) 34　(3) 68　(4) 76　(5) 135

2007年（平成19年）問11　過去問解説

円形テーブルに照射される光束 $ϕ$［lm］は、球全体に放射される全光束 3600［lm］に、テーブルの立体角2.36［sr］と球の全方向立体角 4π［sr］の比を掛けて求めます。

全方向の立体角は 4π［sr］
そのうちの 2.36［sr］分の光束がテーブルに向ってるということなので、テーブルに当たる全光束は

$ϕ=3600×\displaystyle\frac{2.36}{4π}≒676$［lm］

平均照度 $E$［lx］は、テーブルに当たる全光束をテーブルの面積で割ると、求めることができます。

$E=\displaystyle\frac{676}{20}≒34$［lx］

答え (2)

2010年（平成22年）問17

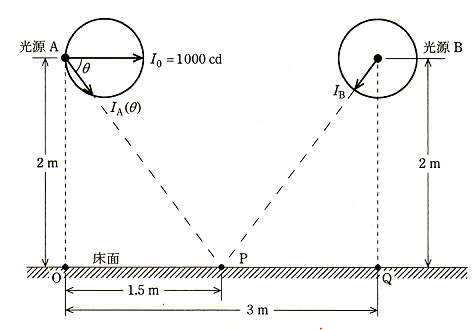
図に示すように、床面上の直線距離 3［m］離れた点 O 及び点 Q それぞれの真上 2［m］のところに、配光特性の異なる 2 個の光源 A，B をそれぞれ取り付けたとき、$\overline{ OQ }$ 線上の中点 P の水平面照度に関して、次の(a)及び(b)に答えよ。
ただし、光源 A は床面に対し平行な方向に最大光度 $I_0$［cd］で、この $I_0$ の方向と角 $θ$ をなす方向に $I_A(θ)＝1000cosθ$［cd］の配光をもつ。光源 B は全光束 5000［lm］で、どの方向にも光度が等しい均等放射光源である。

(a) まず、光源Aだけを点灯したとき、点Pの水平面照度［lx］の値として、最も近いのは次のうちどれか。

(1) 57.6　(2) 76.8　(3) 96.0　(4) 102　(5) 192

(b) 次に、光源Aと光源Bの両方を点灯したとき、点Pの水平面照度［lx］の値として、最も近いのは次のうちどれか。

(1) 128　(2) 141　(3) 160　(4) 172　(5)256

2010年（平成22年）問17　過去問解説

(a) 図に示します。

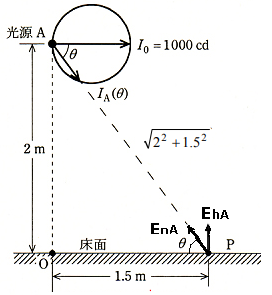
図より、水平面照度 $E_{hA}$［lx］は、

$E_{hA}=E_{nA}sinθ$［lx］

距離の逆2乗の法則より

$\begin{eqnarray}E_{hA}&=&\displaystyle\frac{I_A(θ)}{(\sqrt{2^2+1.5^2})^2}×sinθ\\\\&=&\displaystyle\frac{1000×\displaystyle\frac{1.5}{\sqrt{2^2+1.5^2}}}{6.25}×\displaystyle\frac{2}{\sqrt{2^2+1.5^2}}\\\\&=&76.8［lx］\end{eqnarray}$

答え (2)

(b) 点光源Bの光度 $I_B$［cd］は、球全体に放射される全光束 5000［lm］に、球の全方向立体角 4π［sr］を割ると求めることができます。

$I_B=\displaystyle\frac{5000}{4π}≒398.1$［cd］

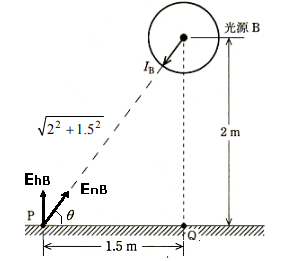
図より、水平面照度 $E_{hB}$［lx］は、

$E_{hB}=E_{nB}sinθ$［lx］

距離の逆2乗の法則より

$\begin{eqnarray}E_{hB}&=&\displaystyle\frac{I_B}{(\sqrt{2^2+1.5^2})^2}×sinθ\\\\&=&\displaystyle\frac{398.1}{6.25}×\displaystyle\frac{2}{\sqrt{2^2+1.5^2}}\\\\&≒&50.96［lx］\end{eqnarray}$

点Pの水平面照度 $E_h$［lx］は、

$E_h=E_{hA}+E_{hB}=76.8+50.96≒128$［lx］

答え (1)

2014年（平成26年）問17

均等放射の球形光源（球の直径は 30cm）がある。床からこの球形光源の中心までの高さは 3mである。また、球形光源から放射される全光束は 12000lmである。次の(a)及び(b)の問に答えよ。

(a) 球形光源直下の床の水平面照度の値［lx］として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、天井や壁など、周囲からの反射光の影響はないものとする。

(1) 35　(2) 106　(3) 142　(4) 212　(5) 425

(b) 球形光源の光度の値［cd］と輝度の値［cd/m²］との組合せとして、最も近いものを次の(1)～(5)のうちから一つ選べ。

　　 光度　　　 輝度
(1)　1910　　 1010
(2)　955　　　3380
(3)　955　　　13500
(4)　1910　　 27000
(5)　3820　　 13500

2014年（平成26年）問17　過去問解説

(a) 光度 $I$［cd］は、球全体に放射される全光束 12000［lm］に、球の全方向立体角 4π［sr］を割ると求めることができます。

$I=\displaystyle\frac{12000}{4π}≒955.4$［cd］

水平面照度 $E$［lx］とすると、距離の逆2乗の法則より

$E=\displaystyle\frac{955.4}{3^2}≒106$［lx］

答え (2)

(b) ランプの光度を $I≒955.4$［cd］とすると、輝度 $L$［cd/m²］は、

$L=\displaystyle\frac{I}{S’}=\displaystyle\frac{955.4}{\displaystyle\frac{π×0.3^2}{4}}≒13500$［cd/m²］

答え (3)

2015年（平成27年）問16

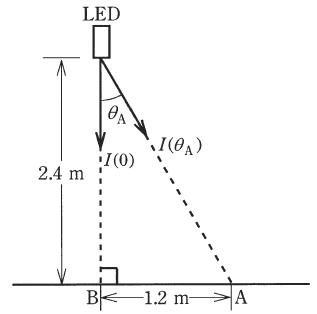
図に示すように、LED1個が、床面から高さ 2.4mの位置で下向きに取り付けられ、点灯している。このLEDの直下方向となす角（鉛直角）をθとすると、このLEDの配光特性（θ方向の光度I(θ)）は、LED直下方向光度I(0)を用いてI(θ)＝I(0)cosθで表されるものとする。次の(a)及び(b)の問に答えよ。

(a) 床面A点における照度が 20lx であるとき、A点がつくる鉛直角θ_Aの方向の光度I(θ_A)の値［cd］として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、このLED以外に光源はなく、天井や壁など、周囲からの反射光の影響もないものとする。

(1) 60　(2) 119　(3) 144　(4) 160　(5) 319

(b) このLED直下の床面B点の照度の値［lx］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 25　(2) 28　(3) 31　(4) 49　(5) 61

2015年（平成27年）問16　過去問解説

(a) 図より、床面A点の水平面照度 $E_{hA}$［lx］は、

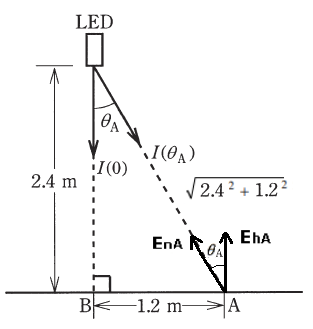
$E_{hA}=E_{nA}cosθ$［lx］

距離の逆2乗の法則より

$\begin{eqnarray}E_{hA}&=&\displaystyle\frac{I(θ_A)}{(\sqrt{2.4^2+1.2^2})^2}×cosθ\\\\&=&\displaystyle\frac{I(θ_A)}{7.2}×\displaystyle\frac{2.4}{\sqrt{2.4^2+1.2^2}}\\\\&=&\displaystyle\frac{I(θ_A)}{7.2}×\displaystyle\frac{2.4}{\sqrt{7.2}}\end{eqnarray}$

題意より $E_{hA}=20$［lx］ですので、

$\displaystyle\frac{I(θ_A)}{7.2}×\displaystyle\frac{2.4}{\sqrt{7.2}}=20$

$I(θ_A)≒160$［cd］

答え (4)

(b) $I(0)$ と $I(θ_A)$ の関係は、

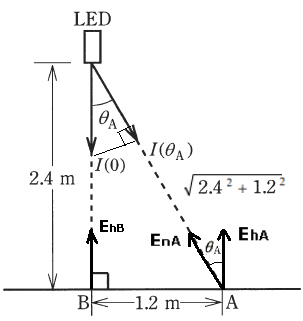
$cosθ_A=\displaystyle\frac{I(θ_A)}{I(0)}$

$\displaystyle\frac{2.4}{\sqrt{2.4^2+1.2^2}}=\displaystyle\frac{160}{I(0)}$

$I(0)≒180$［cd］

床面B点の照度 $E_{hB}$ は、距離の逆2乗の法則より、

$E_{hB}=\displaystyle\frac{I(0)}{2.4^2}=\displaystyle\frac{180)}{2.4^2}≒31$［lx］

答え (3)

2017年（平成29年）問17

均等拡散面とみなせる半径 0.3mの円板光源がある。円板光源の厚さは無視できるものとし、円板光源の片面のみが発光する。円板光源中心における法線方向の光度 $I_0$ は 2000cd であり、鉛直角$θ$方向の光度 $I_θ$ は $I_θ=I_0cosθ$ で与えられる。また、円板光源の全光束 $F$［lm］は $F=πI_0$で与えられるものとする。次の(a)及び(b)の問に答えよ。

(a) 図1に示すように、この円板光源を部屋の天井面に取り付け、床面を照らす方向で部屋の照明を行った。床面B点における水平面照度の値［lx］とB点から円板光源の中心を見たときの輝度の値［cd/m²］として、最も近い値の組合せを次の(1)～(5)のうちから一つ選べ。ただし、この部屋にはこの円板光源以外に光源はなく、天井、床、壁など、周囲からの反射光の影響はないものとする。

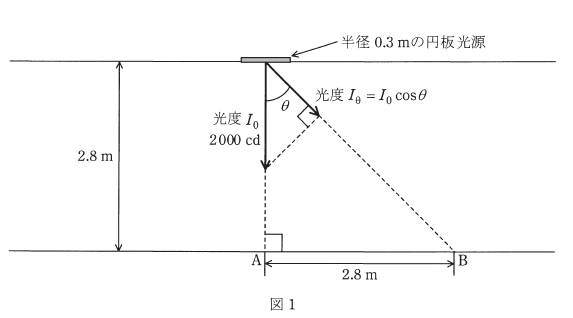
水平面照度［lx］　　輝度［cd/m²］
(1)　　　64　　　　　　　5000
(2)　　　64　　　　　　　7080
(3)　　　90　　　　　　　1060
(4)　　　90　　　　　　　1770
(5)　　 255　　　　　　　7080

(b) 次に、図2に示すように、建物内を真っすぐ長く延びる廊下を考える。この廊下の天井面には上記円板光源が等間隔で連続的に取り付けられ、照明に供されている。廊下の長さは円板光源の取り付け間隔に比して十分に大きいものとする。廊下の床面に対する照明率を 0.3、円板光源の保守率を 0.7としたとき、廊下床面の平均照度の値［lx］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

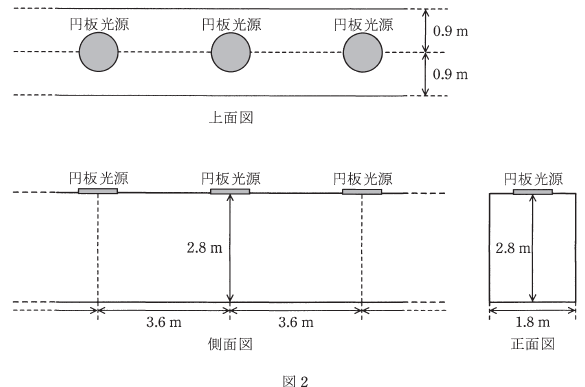
(1) 102　(2) 204　(3) 262　(4) 415　(5) 2261

2017年（平成29年）問17　過去問解説

(a) 図より、床面B点の水平面照度 $E_{hB}$［lx］は、

$E_{hB}=E_{nB}cosθ$［lx］

距離の逆2乗の法則より

$\begin{eqnarray}E_{hB}&=&\displaystyle\frac{I_0cosθ}{(\sqrt{2.8^2+2.8^2})^2}×cosθ\\\\&=&\displaystyle\frac{2000}{2.8^2+2.8^2}×cos^2θ\\\\&=&\displaystyle\frac{2000}{2.8^2+2.8^2}×\left(\displaystyle\frac{2.8}{\sqrt{2.8^2+2.8^2}}\right)^2\\\\&=&\displaystyle\frac{2000×2.8^2}{(2.8^2+2.8^2)^2}\\\\&≒&64［lx］\end{eqnarray}$

円形光源の見かけの面積を$S’$［m²］とすると、輝度 $L$［cd/m²］は、

$L=\displaystyle\frac{I_0cosθ}{S’}$
　$=\displaystyle\frac{I_0cosθ}{π×0.3^2×cosθ}$
　$=\displaystyle\frac{2000}{π×0.3^2}≒7080$［cd/m²］

答え (2)

(b) 1スパンの廊下床面積を $A$［m²］、照明器具1台当たりの光束を $F$［lm］、照明率を $U$、保守率を $M$ とすると、平均照度 $E$［lx］は、

$E=\displaystyle\frac{FMU}{A}=\displaystyle\frac{2000π×0.3×0.7}{3.6×1.8}=204$［lx］

答え (2)