このページでは、変圧器の損失と効率について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された変圧器の損失と効率の過去問題の解き方も解説しています。
- 変圧器の損失
- 無負荷損とその測定
- 負荷損とその測定
- 変圧器の効率
- 温度上昇と温度測定
- 電験三種-機械(変圧器)過去問
- 1999年(平成11年)問12
- 1999年(平成11年)問12 過去問解説
- 2001年(平成13年)問6
- 2001年(平成13年)問6 過去問解説
- 2002年(平成14年)問5
- 2002年(平成14年)問5 過去問解説
- 2003年(平成15年)問16
- 2003年(平成15年)問16 過去問解説
- 2004年(平成16年)問16
- 2004年(平成16年)問16 過去問解説
- 2007年(平成19年)問7
- 2007年(平成19年)問7 過去問解説
- 2008年(平成20年)問16
- 2008年(平成20年)問16 過去問解説
- 2011年(平成23年)問7
- 2011年(平成23年)問7 過去問解説
- 2013年(平成25年)問15
- 2013年(平成25年)問15 過去問解説
- 2016年(平成28年)問8
- 2016年(平成28年)問8 過去問解説
- 2017年(平成29年)問8
- 2017年(平成29年)問8 過去問解説
変圧器の損失
変圧器の効率は、一般に99%以上というようにきわめて良好ですが、それでも変圧器の内部には損失があります。変圧器の内部の損失は、図1に示します。
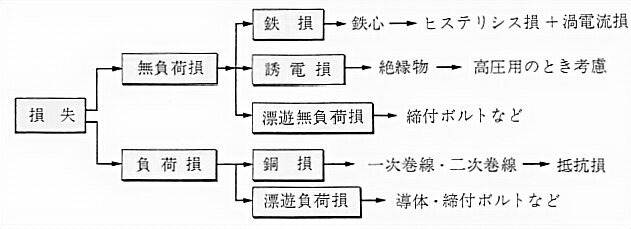
二次側に負荷が接続されていない無負荷のときも、一次側に電源が接続されているため電流が流れて発生する損失を「無負荷損」といい、二次側に負荷が接続されているときに発生する損失を「負荷損」といいます。
これらの損失のうちで大きなものは、「鉄損」と「銅損」です。鉄損は、鉄心中の損失で「ヒステリシス損」と「渦電流損」からなります。銅損は、一次巻線・二次巻線に流れる電流によるジュール熱で抵抗損ともよばれます。
なお、無負荷時に発生する損失は鉄損のみで、負荷時に発生する損失は鉄損と銅損になります。
変圧器の損失を求める式
$損失=P_i+P_c$
$P_i$[W]:鉄損
$P_c$[W]:銅損
銅損を求める式
$P_c=I^2R$
$P_c$[W]:銅損
$I$[A]:巻線に流れる電流
$R$[Ω]:巻線の抵抗
無負荷損とその測定
変圧器の巻線に定格電圧が加わっている場合、負荷が接続されていないときでも、励磁電流による損失分がつねに電力として供給されており、この損失は無負荷損とよばれます。大部分は鉄損ですが、そのほかに、わずかですが、一次巻線抵抗による銅損、絶縁物中の誘電損、締付ボルトなどの金属材料の中に誘導される渦電流による漂遊無負荷損などが含まれます。
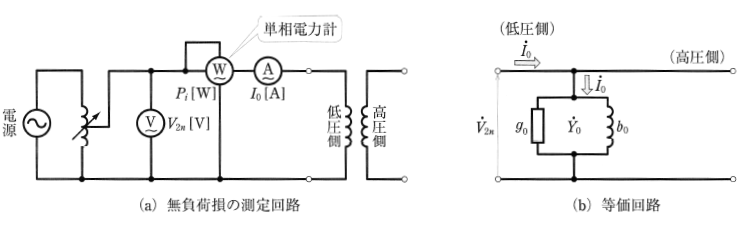
無負荷損を測定するには、図2(a)に示すように、高圧側の回路を無負荷にして低圧側の回路に定格電圧 $V_{2n}$[V]を加え、電力計Wの指示 $P_i$[W]を調べます。このように、変圧器に負荷をかけないで行う試験を無負荷試験といいます。無負荷試験を行うと次のことがわかります。図2(a)において、電圧計Vの指示 $V_{2n}$[V]、電流計Aの指示 $I_o$[A]、電力計Wの指示 $P_i$[W]がわかれば、次の式から、図(b)に示される等価回路の $g_o$[S],$b_o$[S]、および無負荷時の力率 $cosθ_o$ を求めることができます。
$g_o=\displaystyle\frac{P_i}{{V_{2n}}^2}$,$b_o=\sqrt{\left(\displaystyle\frac{I_o}{V_{2n}}\right)^2-\left(\displaystyle\frac{P_i}{{V_{2n}}^2}\right)^2}$
$cosθ_o=\displaystyle\frac{P_i}{V_{2n}I_o}$
負荷損とその測定
定格電圧が加わり、負荷電流が流れているときには、無負荷損とともに銅損が生じます。また、大きな負荷電流のため、漏れ磁束も多くなり、外箱や締付ボルトなどに生じる渦電流が増加します。この種の損失は漂遊負荷損とよばれ、銅損の10~25%です。
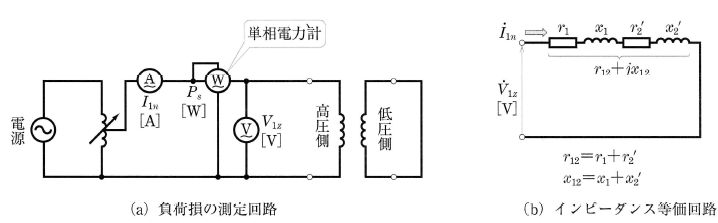
一般に、負荷電流が流れることによって生じる損失を負荷損といい、銅損と漂遊負荷損からなります。負荷損を測定するには、図3(a)に示すように、低圧側の回路を短絡して、インピーダンス電圧 $V_{1Z}$[V]を加え、一次定格電流 $I_{1n}$[A]の電流を流し、電力計Wの読み $P_s$[W]によって求めます。このときの $P_s$[W]はインピーダンスワットとよばれ、巻線の銅損に漂遊負荷損を含めたものです。このように、低圧側を短絡して行う試験を短絡試験といいます。
短絡試験を行うと、インピーダンスワット $P_s$[W]がわかるとともに、図(b)の等価回路で示される抵抗 $r_{12}$[Ω]、リアクタンス $x_{12}$[Ω]を求めることができます。抵抗 $r_{12}$[Ω]およびリアクタンス $x_{12}$[Ω]は次の式で表すことができます。
$r_{12}=\displaystyle\frac{P_s}{{I_{1n}} ^2 }$
$x_{12}=\sqrt{\left(\displaystyle\frac{V_{1Z}}{I_{1n}}\right)^2-\left(\displaystyle\frac{P_s}{{I_{1n}}^2}\right)^2}$
この式で示す $r_{12}$[Ω]は、一次・二次巻線の一次側換算抵抗だけではなく、漂遊負荷損を表す等価抵抗を含んだものです。
なお、一般に無負荷損は、ほとんどが鉄損であり、温度による変化は少ないですが、負荷損は、温度によってある程度変化します。電気機器の試験ではふつう75℃を基準温度としているから、短絡試験で得た $P_s$[W]や $r_{12}$[Ω]は温度補正を行う必要があります。すなわち、測定したときの温度における値を75℃の値に換算します。
変圧器の効率
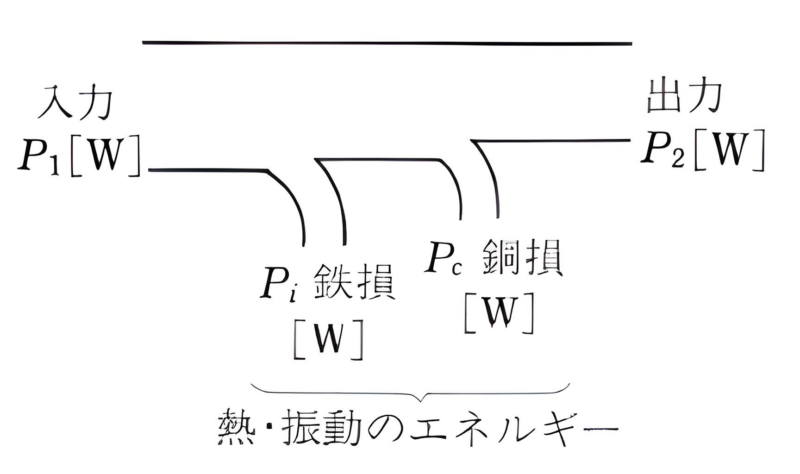
変圧器の出力と入力との比を変圧器の効率といいます。変圧器では、鉄損・銅損などの損失があるので、入力のすべてが出力にはなりません。損失が大きくなると変圧器の効率は小さくなります。入力から出力に至るエネルギーの出入りを図4に示します。
実測効率と規約効率
変圧器の効率には、出力と入力の測定値を用いて計算した「実測効率」と規格に定められた「規約効率」とがあります。
実測効率は、変圧器の容量が大きくなると、それに応じた電源設備を必要とするため、実現しにくいことが多いですが、規約効率は、無負荷試験や短絡試験を行い、内部の温度が75℃になった場合の抵抗値や負荷損に換算して効率を算出します。このことから、変圧器の場合、効率 $η$[%]の標準は規約効率によって表すことになっています。
実測効率を求める式
$η=\displaystyle\frac{出力}{入力}×100$
$η$[%]:効率
規約効率を求める式
$\begin{eqnarray}η&=&\displaystyle\frac{出力}{出力+無負荷損+負荷損}×100\\\\&=&\displaystyle\frac{P_2}{P_2+P_i+P_c}×100\\\\&=&\displaystyle\frac{V_{2n}I_{2n}cosθ}{V_{2n}I_{2n}cosθ+P_i+P_c}×100 \end{eqnarray}$
$η$[%]:効率
$P_i$[W]:鉄損
$P_c$[W]:銅損
$P_2$[W]:二次定格出力
$V_{2n}$[V]:二次定格電圧
$I_{2n}$[A]:二次定格電流
$cosθ$:負荷の力率
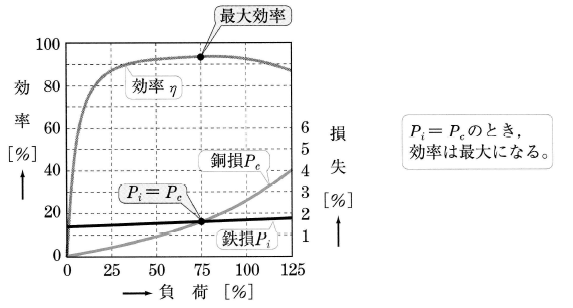
負荷の大きさと効率との関係を図5に示します。変圧器は、一般に負荷電流が定格電流の75%(3/4負荷)程度のとき最大効率を示すように設計されています。鉄損=銅損のとき、変圧器の効率 η[%]は最大効率を示します。
負荷比
負荷 $K$[VA]と変圧器定格容量 $P$[VA]との比を負荷比 $a=\displaystyle\frac{K}{P}$ とすると、二次定格出力 $P_2$[W]との関係は次のようになります。
$P_2=Kcosθ=aPcosθ$
負荷比 $a$ とは「全容量の何%で運転しているか」を表すもので、負荷比 $a$ で運転しているときの変圧器の効率を求める式は次のようになります。
負荷比 $a$ で運転しているときの変圧器の効率を求める式
$η=\displaystyle\frac{aPcosθ}{aPcosθ+P_i+a^2P_{cn}}×100$
$η$[%]:効率
$P$[VA]:変圧器の定格容量
$P_i$[W]:鉄損
$P_{cn}$[W]:全負荷時の銅損
$cosθ$:負荷の力率
$a$:負荷比
全日効率
変圧器の二次側の負荷は時間とともに変動しますが、一次側ではつねに電圧が加わってぃるので、負荷の大小に関係なく、鉄損が生じています。このことから、変圧器の効率のよい利用のされ方を表すために「全日効率」が使われます。全日効率 $ηd$[%]は、 1日を通しての出力電力量と入力電力量との比であり、次の式で表すことができます。
$ηd=\displaystyle\frac{1日の出力電力量[kW・h]}{1日の入力電力量[kW・h]}×100$
1日のうち、全負荷出力 $P$[kW]で $t$ 時間変圧器が運転されたときの全日効率 $ηd$[%]は、次の式で表すことができます。
全日効率を求める式
$ηd=\displaystyle\frac{Pt}{Pt+24P_i+P_ct}×100$
$ηd$[%]:全日効率
$P$[VA]:変圧器の定格容量
$P_i$[W]:鉄損
$P_{c}$[W]:銅損
$cosθ$:負荷の力率
$t$:変圧器を運転した時間
$24P_i$ と $P_ct$ の関係から、両者が等しい場合に、全日効率は最大となります。したがって、1日中無負荷運転に近い変圧器は、鉄損の小さい巻鉄心形が適しています。また、1日中全負荷運転に近い変圧器は、銅損を少なくした設計のものが用いられます。
また、負荷比 $a$ で運転しているときの変圧器の全日効率 $ηd$[%]は、次の式で表すことができます。
負荷比 $a$ で運転している変圧器の全日効率を求める式
$ηd=\displaystyle\frac{aPcosθt}{aPcosθt+24P_i+a^2P_{cn}t}×100$
$ηd$[%]:全日効率
$P$[VA]:変圧器の定格容量
$P_i$[W]:鉄損
$P_{cn}$[W]:全負荷時の銅損
$cosθ$:負荷の力率
$a$:負荷比
$t$:変圧器を運転した時間
温度上昇と温度測定
変圧器に定格負荷を接続して運転すると、内部に鉄損と銅損を生じ、巻線の温度が上昇し、ついには一定温度に達します。この温度を最終温度といいます。最終温度が使用している絶縁物の許容最高温度を超えないようにしなければなりません。
温度の測定には、図6(a),(b)に示すように、温度計を用いる方法と、抵抗温度係数を利用して測定する方法とがあります。大形の変圧器などでは、温度測定のために、測温抵抗(銅線など)があり、その抵抗をブリッジで測定し、温度を知ることができるようになっているものが多いです。
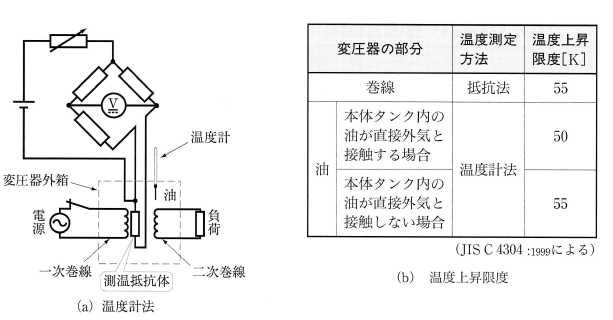
常温 $t$[℃]のときの抵抗値を $R_t$[Ω]とし、上昇後の温度 $T$ を 75[℃]としたときの抵抗値 $R_{75}$ は、次の式で表すことができます。
$R_{75}=\displaystyle\frac{234.5+T}{234.5+t}R_t=\displaystyle\frac{309.5}{234.5+t}R_t$
規約効率を計算する場合、測定した抵抗値 $R_t$ を式を用いて $R_{75}$ に補正します。そして、この値を用いて効率を計算します。
電験三種-機械(変圧器)過去問
1999年(平成11年)問12
ある変圧器の負荷力率 100[%]における全負荷効率は 99.0[%]である。この変圧器の負荷力率 80[%]における全負荷効率[%]の値として、正しいのは次のうちどれか。
(1) 79.2 (2) 84.2 (3) 88.7 (4) 93.8 (5) 98.8
1999年(平成11年)問12 過去問解説
二次定格出力を $P_2$[W]、鉄損を $P_i$[W]、銅損を $P_c$[W]とすると、効率 $η$[%]は、
$η=\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100$
負荷力率 100[%]のとき、全負荷効率は 99.0[%]ですので、
$η_{100}=\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100$
$99.0=\displaystyle\frac{P_2×1}{P_2×1+P_i+P_c}×100$
$0.99(P_2+P_i+P_c)=P_2$
$P_i+P_c=0.01P_2$
負荷力率 80[%]における全負荷効率 $η_{80}$[%]は、
$\begin{eqnarray}η_{80}&=&\displaystyle\frac{P_2×0.8}{P_2×0.8+P_i+P_c}×100\\\\&=&\displaystyle\frac{0.8P_2}{0.8P_2+0.01P_2}×100\\\\&=&\displaystyle\frac{0.8P_2}{0.81P_2}×100\\\\&=&98.8[\%]\end{eqnarray}$
答え (5)
2001年(平成13年)問6
ある単相変圧器の負荷が、全負荷の 1/2 のときに効率が最大になるという。この変圧器の負荷が全負荷の 3/4 のときの銅損 $P_c$ と鉄損 $P_i$ の比($P_c$/$P_i$) の値として、正しいのは次のうちどれか。
ただし、二次電圧及び負荷力率は一定とする。
(1) 0.56 (2) 1.13 (3) 1.50 (4) 2.25 (5) 3.00
2001年(平成13年)問6 過去問解説
変圧器の負荷を全負荷の $\displaystyle\frac{1}{n}$ にしたとき、電流は $\displaystyle\frac{1}{n}I_{2n}$ となり、銅損は $\left(\displaystyle\frac{1}{n}I_{2n}\right)^2r_{21}=\left(\displaystyle\frac{1}{n}\right)^2P_c$ となります。鉄損 $P_i$ は負荷の大きさに関係なく一定です。
したがって、負荷が $\displaystyle\frac{1}{2}$ になった時の銅損は、$\left(\displaystyle\frac{1}{2}\right)^2P_c$ となります。このとき、効率が最大になるということは、銅損 $P_c$ =鉄損 $P_i$ ですので、
$\left(\displaystyle\frac{1}{2}\right)^2P_c=P_i$
負荷が $\displaystyle\frac{3}{4}$ になった時の銅損 $P_c$ と鉄損 $P_i$ の比($P_c$/$P_i$) は、
$\displaystyle\frac{\left(\displaystyle\frac{3}{4}\right)^2P_c}{P_i}=\displaystyle\frac{\left(\displaystyle\frac{3}{4}\right)^2P_c}{\left(\displaystyle\frac{1}{2}\right)^2P_c}≒2.25$
答え (4)
2002年(平成14年)問5
単相変圧器がある。定格二次電圧 200[V]において、二次電流が 250[A]のときの全損失が 1,525[W]であり、また、二次電流が 150[A]のときの全損失が 1,125[W]であった。この変圧器の無負荷損[W]の値として、正しいのは次のうちどれか。
(1) 400 (2) 525 (3) 576 (4) 900 (5) 1005
2002年(平成14年)問5 過去問解説
銅損(負荷損)を $P_c$[W]、鉄損(無負荷損)を $P_i$[W]とすると、全損失≒$P_c+P_i$ となります。また、鉄損 $P_i$ は負荷の大きさに関係なく一定です。$P_c=rI^2$ より、
$1525=r×250^2+P_i$
$1125=r×150^2+P_i$
これを解くと、
$P_i=900$[W]
答え (4)
2003年(平成15年)問16
単相変圧器があり、負荷 86[kW]、力率1.0で使用したときに最大効率 98.7[%]が得られる。この変圧器について、次の(a)及び(b)に答えよ。
(a) この変圧器の無負荷損[W]の値として、最も近いのは次のうちどれか。
(1) 466 (2) 566 (3) 667 (4) 850 (5) 1,133
(b) この変圧器を負荷20[kW]、力率1.0で使用したときの効率[%]の値として、最も近いのは次のうちどれか。
(1) 94.4 (2) 95.7 (3) 96.6 (4) 97.1 (5)97.6
2003年(平成15年)問16 過去問解説
(a) 効率が最大になるということは、銅損(負荷損) $P_c$ =鉄損(無負荷損) $P_i$ ですので、効率 $η$[%]は、
$η=\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100$
$98.7=\displaystyle\frac{86×10^3×1.0}{86×10^3×1.0+2P_i}×100$
$86×10^3+2P_i=\displaystyle\frac{86×10^3}{0.987}$
$P_i≒566$[W]
答え (2)
(b) 銅損(負荷損)は、一次巻線・二次巻線に流れる電流によるジュール熱($rI^2$)ですので、抵抗の2乗に比例します。電圧が一定と考えると、負荷電力の2乗に比例するとも考えることができます。 負荷 ${P_2}’=20$[kW]のときの、銅損を ${P_c}’$[W]とすると、
${P_2} ^2 :{{P_2}’} ^2 =P_c:{P_c}’$
$(86×10^3)^2:(20×10^3)^2=566:{P_c}’$
${P_c}’=\displaystyle\frac{20^2}{86^2}×566$[W]
この時の効率 $η$[%]は、
$\begin{eqnarray}η&=&\displaystyle\frac{{P_2}’}{{P_2}’+P_i+{P_c}’}×100\\\\&=&\displaystyle\frac{20×10^3}{ 20×10^3 +566+\displaystyle\frac{20^2}{86^2}×566}×100\\\\&≒&97.1[\%]\end{eqnarray}$
答え (4)
2004年(平成16年)問16
定格容量 100[kV・A]の変圧器があり、負荷が定格容量の 1/2 の大きさで力率1のときに、最大効率 98.5[%]が得られる。この変圧器について、次の(a)及び(b)に答えよ。
(a) 最大効率 98.5[%]が得られるときの銅損[W]の値として、最も近いのは次のうちどれか。ただし、変圧器の損失のうち、鉄損と銅損以外の損失は無視できるものとする。
(1) 190 (2) 375 (3) 381 (4) 750 (5) 761
(b)この変圧器を、1日のうち8時間は力率0.8の定格容量で運転し、それ以外の時間は無負荷で運転したとき、全日効率[%]の値として、最も近いのは次のうちどれか。
(1) 93.8 (2) 94.6 (3) 95.5 (4) 96.8 (5) 97.7
2004年(平成16年)問16 過去問解説
(a) 鉄損を $P_i$[W]、銅損を $P_c$[W]、効率を $η$[%]とすると、最大効率は $P_i=P_c$ のときですので、
$η=\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100=\displaystyle\frac{P_2cosθ}{P_2cosθ+2P_c}×100$
$98.5=\displaystyle\frac{100×10^3×\displaystyle\frac{1}{2}×1}{100×10^3×\displaystyle\frac{1}{2}×1+2P_c}×100$
$50×10^3=0.985(50×10^3+2P_c)$
$P_c≒381$[W]
答え (3)
(b) 全負荷時の電流は、1/2負荷時の2倍になります。銅損は電流の2乗に比例するので、全負荷時の銅損 ${P_c}’$ は、1/2負荷時の4倍になります。
${P_c}’=4P_c=4×381=1524$
1日のうち、全負荷出力 $P$[kW]で $t$ 時間変圧器が運転されたときの全日効率を $ηd$[%]とすると、
$\begin{eqnarray}ηd&=&\displaystyle\frac{Pt}{Pt+24P_i+{P_c}’t}×100\\\\&=&\displaystyle\frac{100×10^3×0.8×8}{100×10^3×0.8×8+24×381+1524×8}×100&\\\\&≒&96.8[\%]\end{eqnarray}$
答え (4)
2007年(平成19年)問7
単相変圧器の一次側に電流計、電圧計および電力計を接続して、二次側を短絡し、一次側に定格周波数の電圧を供給し、電流計が 40[A]を示すよう一次側の電圧を調整したところ、電圧計は 80[V]、電力計は 1200[W]を示した。この変圧器の一次側からみた漏れリアクタンス[Ω]の値として、最も近いのは次のうちどれか。
ただし、電流計・電圧計及び電力計は理想的な計器であるものとする。
(1) 1.28 (2) 1.85 (3) 2.00 (4) 2.36 (5) 2.57
2007年(平成19年)問7 過去問解説
低圧側の回路を短絡して、インピーダンス電圧 $V_{1Z}$[V]を加え、一次定格電流 $I_{1n}$[A]の電流を流し、電力計Wの読み $P_s$[W]によって求めます。このときの $P_s$[W]はインピーダンスワットとよばれ、巻線の銅損に漂遊負荷損を含めたものです。このように、低圧側を短絡して行う試験を短絡試験といいます。
短絡試験を行うと、インピーダンスワット $P_s$[W]がわかるとともに、図の等価回路で示される抵抗 $r_{12}$[Ω]、リアクタンス $x_{12}$[Ω]を求めることができます。
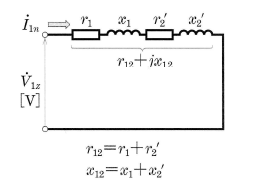
リアクタンス $x_{12}$[Ω]は次の式で求めることができますので、
$\begin{eqnarray}x_{12}&=&\sqrt{\left(\displaystyle\frac{V_{1Z}}{I_{1n}}\right)^2-\left(\displaystyle\frac{P_s}{{I_{1n}}^2}\right)^2}\\\\&=&\sqrt{\left(\displaystyle\frac{80}{40}\right)^2-\left(\displaystyle\frac{1200}{40^2}\right)^2}\\\\&≒&1.85[Ω]\end{eqnarray}$
答え (2)
2008年(平成20年)問16
定格容量 50[kV・A]の単相変圧器がある。この変圧器を定格電圧、力率 100[%]、全負荷の 3/4 の負荷で運転したとき、鉄損と銅損が等しくなり、そのときの効率は 98.2[%]であった。この変圧器について、次の(a)及び(b)に答えよ。
ただし、鉄損と銅損以外の損失は無視できるものとする。
(a) この変圧器の鉄損[W]の値として、最も近いのは次のうちどれか。
(1) 344 (2) 382 (3) 425 (4) 472 (5) 536
(b) この変圧器を全負荷、力率 100[%]で運転した時の銅損[W]の値として、最も近いのは次のうちどれか。
(1) 325 (2) 453 (3) 579 (4) 611 (5) 712
2008年(平成20年)問16 過去問解説
(a) 鉄損を $P_i$[W]、銅損を $P_c$[W]、効率を $η$[%]とすると、最大効率は $P_i=P_c$ のときですので、
$η=\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100$
$\begin{eqnarray}98.2&=&\displaystyle\frac{\displaystyle\frac{3}{4}×50×10^3×1.0}{\displaystyle\frac{3}{4}×50×10^3×1.0+2P_i}×100\\\\&=&\displaystyle\frac{37500}{37500+2P_i}×100\end{eqnarray}$
$P_i=344$[W]
答え (1)
(b) 全負荷時の電流は、3/4負荷時の4/3倍になります。銅損は電流の2乗に比例するので、全負荷時の銅損 ${P_c}’$ は、3/4負荷時の16/9倍になります。したがって、
${P_c}’=344×\displaystyle\frac{16}{9}≒611$[W]
答え (4)
2011年(平成23年)問7
次の文章は、変圧器の損失と効率に関する記述である。
電圧一定で出力を変化させても、出力一定で電圧を変化させても、変圧器の効率の最大は鉄損と銅損とが等しいときに生じる。ただし、変圧器の損失は鉄損と銅損だけとし、負荷の力率は一定とする。
- 出力 1000[W]で運転している単相変圧器において鉄損が 40.0[W]、銅損が 40.0[W]発生している場合、変圧器の効率は( ア )[%]である。
- 出力電圧一定で出力を 500[W]に下げた場合の鉄損は 40.0[W]、銅損は( イ )[W]、効率は( ウ )[%]となる。
- 出力電圧が 20[%]低下した状態で、出力 1000[W]の運転をしたとすると鉄損は 25.6[W]、銅損は( エ )[W]、効率は( オ )[%]となる。
ただし、鉄損は電圧の2乗に比例するものとする。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる最も近い数値の組合せを、次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 94 | 20.0 | 89 | 61.5 | 91 |
| (2) | 93 | 10.0 | 91 | 62.5 | 92 |
| (3) | 94 | 20.0 | 89 | 63.5 | 91 |
| (4) | 93 | 10.0 | 91 | 50.0 | 93 |
| (5) | 92 | 20.0 | 89 | 61.5 | 91 |
2011年(平成23年)問7 過去問解説
a. 鉄損を $P_i$[W]、銅損を $P_c$[W]、効率を $η$[%]とすると、
$\begin{eqnarray}η&=&\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100\\\\&=&\displaystyle\frac{1000×1.0}{1000×1.0+40.0+40.0}×100\\\\&≒&93[\%]\end{eqnarray}$
b. 500[W]負荷時の電流は、1000[W]負荷時の1/2倍になります。銅損は電流の2乗に比例するので、500[W]負荷時の銅損 ${P_c}’$ は、1000[W]負荷時の1/4倍になります。つまり、$40×\displaystyle\frac{1}{4}=10.0$[W]です。このときの、効率 $η’$[%]は、
$\begin{eqnarray}η_2&=&\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100\\\\&=&\displaystyle\frac{500×1.0}{500×1.0+40.0+10.0}×100\\\\&≒&91[\%]\end{eqnarray}$
c. aのときの電流を $I$[A]、電圧を $V$[V]とし、出力電圧が 20[%]低下したときの電流を $I’$[A]、電圧を $V’$[V]とすると、その時の出力 $P’$[W]は、
$P’=I’V’=I'(1-0.2)V=0.8I’V$[W]
aの時と、出力電圧が 20[%]低下したときの出力は、1000[W]で同じですので、
$IV=0.8I’V$
$I’=1.25I$
この時の銅損 ${P_c}”$は、電流が 1.25倍になりますので、
${P_c}”=40×1.25^2=62.5$[W]
このときの、効率 $η”$[%]は、
$η”=\displaystyle\frac{1000×1.0}{1000×1.0+25.6+62.5}×100≒92$[%]
答え (2)
2013年(平成25年)問15
定格容量 10[kV・A]、定格一次電圧 1000[V]、定格二次電圧 100[V]の単相変圧器で無負荷試験及び短絡試験を実施した。高圧側の回路を開放して低圧側の回路に定格電圧を加えたところ、電力計の指示は 80[W]であった。次に、低圧側の回路を短絡して高圧側の回路にインピーダンス電圧を加えて定格電流を流したところ、電力計の指示は 120[W]であった。
(a) 巻線の高圧側換算抵抗[Ω]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.0 (2) 1.2 (3) 1.4 (4) 1.6 (5) 2.0
(b) 力率 cosφ=1 の定格運転時の効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 95 (2) 96 (3) 97 (4) 98 (5) 99
2013年(平成25年)問15 過去問解説
(a) 定格容量を $P_n$ $V_{1n}$[kV・A]、定格一次電圧を $V_{1n}$[V]、定格一次電流を $I_{1n}$[A]、インピーダンスワットを $P_s$[W]、一次・二次巻線の一次側換算抵抗 $x_{12}$[Ω]は、
$I_{1n}=\displaystyle\frac{P_n}{V_{1n}}=\displaystyle\frac{10×10^3}{1000}=10$[A]
$r_{12}=\displaystyle\frac{P_s}{{I_{1n}} ^2 }=\displaystyle\frac{120}{10^2 }=1.2$[Ω]
短絡試験は、二次側を短絡して定格電流を流します。そのときの電力は、インピーダンスワット $P_s$[W]といいます。これは、巻線の銅損に漂遊負荷損を含めたものです。
答え (2)
(b) 鉄損を $P_i$[W]、銅損を $P_c$[W]、効率を $η$[%]とすると、
$\begin{eqnarray}η&=&\displaystyle\frac{P_2cosθ}{P_2cosθ+P_i+P_c}×100\\&=&\displaystyle\frac{10×10^3×1.0}{10×10^3×1.0+80+120}×100\\\\&≒&98[\%]\end{eqnarray}$
無負荷試験は、高圧側の回路を無負荷にして低圧側の回路に定格電圧 $V_{2n}$[V]を加え、電力計Wの指示 $P_i$[W]を調べる試験です。
答え (4)
2016年(平成28年)問8
変圧器の規約効率を計算する場合、巻線の抵抗値を 75℃の基準温度の値に補正する。ある変圧器の巻線の温度と抵抗値を測ったら、20℃のとき 1.0Ωであった。この変圧器の 75℃における巻線抵抗値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、巻線は銅導体であるものとし、T[℃]とt[℃]の抵抗値の比は、(235+T):(235+t)である。
(1) 0.27 (2) 0.82 (3) 1.22 (4) 3.75 (5) 55.0
2016年(平成28年)問8 過去問解説
題意より
(235+75):(235+20)=R:1.0
R=1.22[Ω]
答え (3)
2017年(平成29年)問8
定格容量 50 kV・Aの単相変圧器において、力率1の負荷で全負荷運転したときに、銅損が 1000 W、鉄損が 250 Wとなった。力率 1 を維持したまま負荷を調整し、最大効率となる条件で運転した。銅損と鉄損以外の損失は無視できるものとし、この最大効率となる条件での効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 95.2 (2) 96.0 (3) 97.6 (4) 98.0 (5) 99.0
2017年(平成29年)問8 過去問解説
全負荷運転したときの、銅損 $P_c$ は 1000 W、鉄損 $P_i$ は 250 Wです。鉄損 $P_i$ は負荷の大きさに関係なく一定です。これを、最大効率になるように運転しますので、鉄損 $P_i$ = 銅損 $P_c$ = 250 Wになるときが、最大効率になります。
銅損(負荷損)は、一次巻線・二次巻線に流れる電流によるジュール熱($rI^2$)ですので、銅損が1000Wから250Wになったときの電流値の比を $a$ とすると、
$a=\sqrt{\displaystyle\frac{250}{1000}}=0.5$
電流値は 0.5倍になります。このときの、効率 $η$[%]は、
$\begin{eqnarray}η&=&\displaystyle\frac{aP_2cosθ}{aP_2cosθ+P_i+P_c}×100\\\\&=&\displaystyle\frac{0.5×50×10^3×1.0}{0.5×50×10^3×1.0+250+250}×100\\\\&≒&98.0[\%]\end{eqnarray}$
答え (4)





