このページでは、変圧器の三相結線について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された変圧器の三相結線の過去問題の解き方も解説しています。
△―△結線
図1において、対称三相電源の各端子をU,V ,Wとします。各変圧器 $T_1$,$T_2$,$T_3$ の一次側端子に、$\dot{V}_{UV}$[V],$\dot{V}_{VW}$[V],$\dot{V}_{WU}$[V]の電圧が加わるように接続します。また、二次側端子においても同じように接続します。図1(a)から、変圧器の各端子は、△に結線されていることがわかります。このような結線法を△結線といい、図1に示すように、一次側・二次側とも△結線したものを、変圧器の△―△結線といいいます。図(b)は、△―△結線の接続図です。
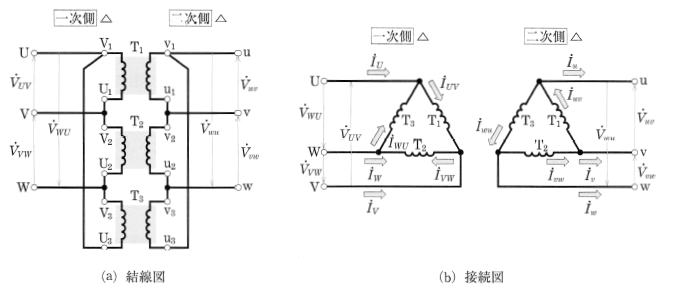
この結線の場合の一次側の電圧・電流のベクトル図は、図2のようになります。△―△結線は、変圧器巻線に流れる電流が線電流の $\displaystyle\frac{1}{\sqrt{3}}$ となり、一次側線間電圧と二次側線間電圧は同相となります。線間電圧と変圧器巻線電圧が等しく、高圧用としては、絶縁の点で不利となりますので、60kV以下の配電用変圧器に用いられます。しかし、3台のうち1台が故障しても残り2台で(V―V結線により)運転可能であり、3台分の容量の $\displaystyle\frac{1}{\sqrt{3}}$ の負荷に対応することができます。
なお、各変圧器の励磁電流には、基本波のほかに第3調波が含まれており、この第3調波は、各相とも同相です。したがって、第3調波電流は、巻線内を循環電流として流れるので高調波電圧が線間電圧に現れず、波形のひずみが生じないので、通信障害がありません。
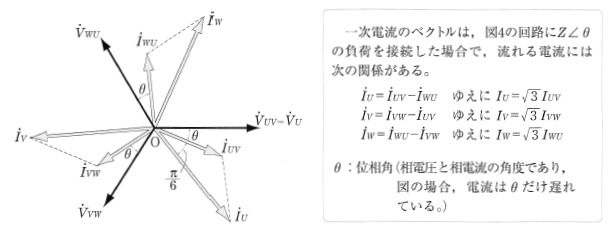
△―△結線の特徴
- 第3高調波は循環するため外部に出ない。
- 1 台故障してもV-V 結線として使用できる。
- 中性点が接地できない。(接地保護が困難)
△―Y結線
図1(a)の各変圧器の一次側は△結線のままにしておき、二次側を図3(a)のように接続する方法を、変圧器の△一Y結線といいます。図(b)にその接続図を示します。この結線のベクトル図を図4に示します。図において、一次電圧 $\dot{V}_{UV}$[V]と二次電圧 $\dot{V}_{uv}$[V]の位相差を角変位といい、$\dot{V}_{UV}$[V]を基準にして、$\dot{V}_{uv}$[V]の位相角を時計まわりにはかった角で表します。したがって、図4の場合の角変位は、330°です。
△―Y結線では、二次側の線間電圧は、相電圧の $\sqrt{3}$倍になり、線電流は相電流に等しくなります。この結線方法は、送電線の送電端(発電所)などのように、電圧を高くする場合に用いられます。
一次側に△結線があるので、第3調波電流は巻線内を循環し、二次側には流れないので通信障害がありません。また、Y結線の中性点が接地できるなどの特徴があります。
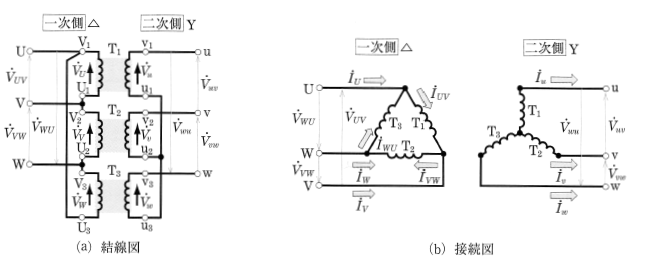
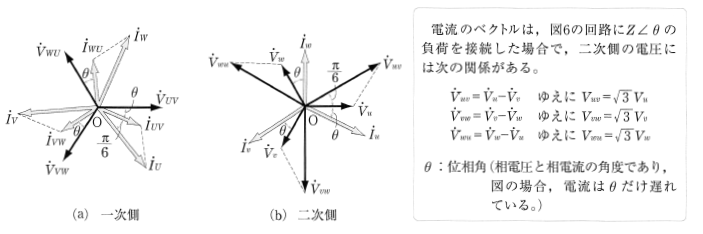
△―Y結線の特徴
- 中性点が接地できる。(接地保護が容易)
- 一次電圧に対し二次電圧の位相が30° 進みになる。
- 発電所の昇圧用に使われる。
Y―△結線
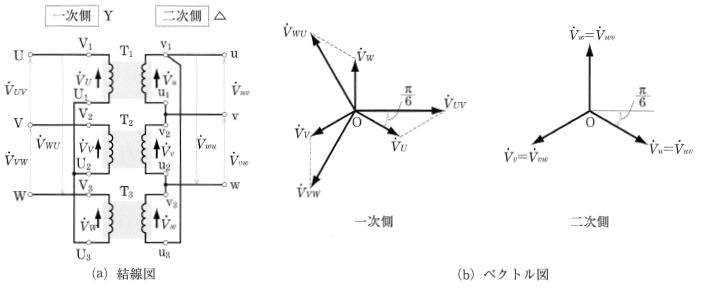
図5(a)に示すように、各変圧器の一次側をY結線、二次側を△結線したものを、変圧器のY―△結線といいます。図(b)はこの結線の電圧ベクトル図であり、二次側では、線間電圧と相電圧は等しくなりますい。Y一△結線は、送電線の受電端などのように、電圧を低くする場合に用いられます。
Y―△結線の特徴
- 中性点が接地できる。(接地保護が容易)
- 一次電圧に対し二次電圧の位相が30° 遅れになる。
- 発電所の降圧用に使われる。
Y―Y結線
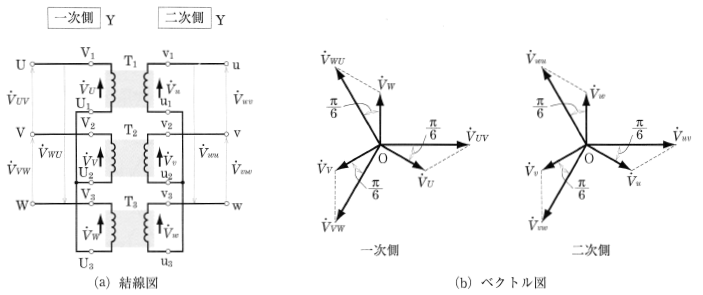
図6(a)に示すように、各変圧器の一次および二次側をY結線したものを、変圧器のY一Y結線といます。図(b)は、一次側・二次側の電圧ベクトル図です。ベクトル図から、線間電圧は相電圧の $\sqrt{3}$倍になります。
Y―Y結線には、第3調波の流れる回路がないため、電圧波形がひずみ、これが原因となって、近くの通信線に雑音などの障害を与えます。このため、Y―Y結線は、変圧器の絶縁が他の方法より容易であるなどの利点がありますが、特別な場合のほかは使用されません。
Y―Y結線の特徴
- 中性点が接地できる。(接地保護が容易)
- 第3 高調波が発生するため誘導障害(通信障害)を起こす。そのためほとんど使用されない。使用する場合は、Δ 結線を加えたY-Y-Δ 結線が使われる。
V―V結線
単相変圧器2台を用いて、図7に示すように結線する方法を、V―V結線といいます。3台の単相変圧器を用いて△―△結線したものから、1台の変圧器を取り除くとV―V結線になります。
結線は、各変圧器の端子記号に注意して、図(a)のように行います。図(b)にその接続図を示します。
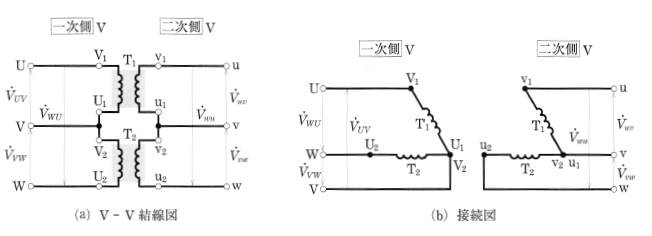
図8(a)の結線において、一次側に対称三相電圧 $\dot{V}_{UV}$[V],$\dot{V}_{VW}$[V],$\dot{V}_{WU}$[V]を加えたとき、二次側の各線間電圧は、一次側に加えた電圧 $\dot{V}_{UV}$[V]によって、変圧器 $T_1$ の一次巻線に $\dot{V}_{U}$[V]の電圧が誘導され、二次巻線には $\dot{V}_{u}$[V]の電圧が誘導されます。また同様に、$T_2$ の各巻線には $\dot{V}_{V}$[V],$\dot{V}_{v}$[V]の電圧が誘導されます。
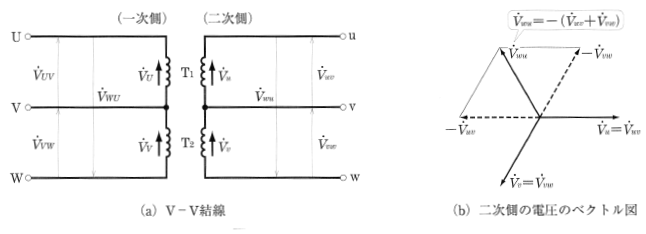
このことから、図8(b)の二次線間電圧 $\dot{V}_{uv}$[V],$\dot{V}_{vw}$[V]、および図(a)から、端子w,u間の電圧 $\dot{V}_{wu}$[V]の間には次の関係があります。
$\dot{V}_{wu}=-(\dot{V}_{uv}+\dot{V}_{vw})$
各電圧の関係をベクトル図に示すと、図(b)になり、$\dot{V}_{uv}$[V],$\dot{V}_{vw}$[V],$\dot{V}_{wu}$[V]は対称三相電圧であることがわかります。
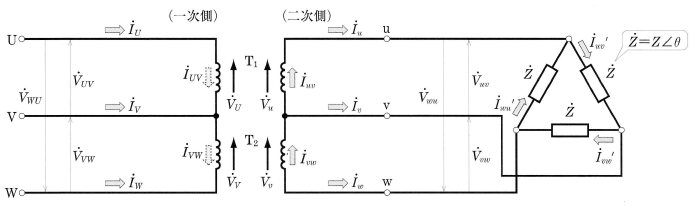
図9に示すように、変圧器の二次側に平衡二相負荷を接続すると、各負荷に流れる相電流 $\dot{I}_{uv}$’[A],$\dot{I}_{vw}$’[A],$\dot{I}_{wu}$’[A]、二次側の各線の電流 $\dot{I}_{u}$[A],$\dot{I}_{v}$[A],$\dot{I}_{w}$[A]の間には、次の関係があります。
$\dot{I}_{u}={\dot{I}_{uv}}’-{\dot{I}_{wu}}’$,$\dot{I}_{v}={\dot{I}_{vw}}’-{\dot{I}_{uv}}’$ ,$\dot{I}_{w}={\dot{I}_{wu}}’-{\dot{I}_{vw}}’$
また、各変圧器の二次巻線に流れる電流 $\dot{I}_{uv}$[A],$\dot{I}_{vw}$[A]は、次の式で表すことができます。
$\dot{I}_{uv}=\dot{I}_{u}$[A],$\dot{I}{vw}=-\dot{I}_w$
なお、変圧器の一次巻線に流れる電流 $\dot{I}_{UV}$,$\dot{I}_{VW}$[A]は、変圧比 $a$ を用いると、二次巻線電流に対して、次の式で表すことができます。
$\dot{I}_{UV}=\displaystyle\frac{1}{a}\dot{I}_{uv}=\dot{I}_{U}$,$-\dot{I}_{VW}=-\displaystyle\frac{1}{a}\dot{I}_{vw}=\dot{I}_{W}$
以上の電圧や電流の関係をベクトル図に示すと、図10になります。変圧器 $T_1$ の出力を $P_1$[W]、変圧器 $T_2$ の出力を $P_2$[W]とすると、V―V結線の出力 $P_V$[W]は、次の式で表すことができます。
$\begin{eqnarray}P_V&=&P_1+P_2\\\\&=&V_{uv}I_{uv}cos(\displaystyle\frac{π}{6}+θ)+V_{uw}I_{uw}cos(\displaystyle\frac{π}{6}-θ)\end{eqnarray}$
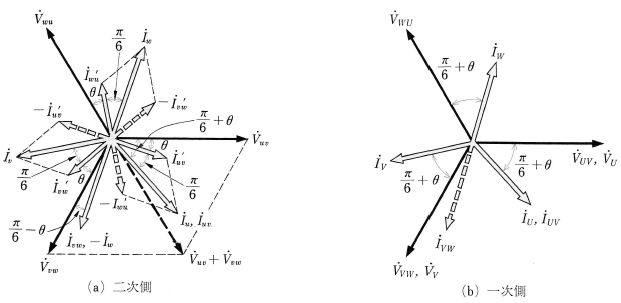
線間電圧および負荷は平衡していますので、定格状態では、$V_{uv}=V_{vw}=V_n$,$I_{uv}=I_{vw}=I_n$ とおくと、次の式で表すことができます。
$\begin{eqnarray}P_V&=&V_nI_n\left[cos(\displaystyle\frac{π}{6}+θ)+cos(\displaystyle\frac{π}{6}-θ)\right]\\\\&=&\sqrt{3}V_nI_ncosθ=\sqrt{3}P\end{eqnarray}$
V―V結線の最大出力[W]は、変圧器1台の定格容量 $P$($=V_nI_ncosθ$)の $\sqrt{3}$ 倍になることがわかります。V―V結線では2台の変圧器を用いますので、容量は2Pですが、実際には $\sqrt{3}P$ しか利用できないことになります。設備の容量がどれだけ有効に利用されているかを表す場合、利用率を用いますが、V―V結線の変圧器の利用率は次の式から求めることができます。
$利用率=\displaystyle\frac{V結線の出力}{設備容量}=\displaystyle\frac{\sqrt{3}P}{2P}=\displaystyle\frac{\sqrt{3}}{2}$
これは、V―V結線により得られる出力は、2台分の出力の86.6%であることを示しています。また、△―△結線の出力 $P_{Δ}$ を $P_{Δ}=3P$、V―V結線の出力 $P_V$ を $P_V=\sqrt{3}P$ とすると、出力比は次の式から求めることができます。
$出力比=\displaystyle\frac{V結線の出力}{△結線の出力}=\displaystyle\frac{\sqrt{3}P}{3P}=\displaystyle\frac{1}{\sqrt{3}}$
これは、変圧器3台で運転していたときの出力に対して、57.7%の出力しか得られないことを示しています。
電験三種-機械(変圧器)過去問
2003年(平成15年)問8
定格容量 500[kVA]の単相変圧器3台をΔ-Δ結線1バンクとして使用している。ここで、同一仕様の単相変圧器1台を追加し、V-V結線2バンクとして使用するとき、全体として増加させることができる三相容量[kVA]の値として、最も近いのは次のうちどれか。
(1) 134 (2) 232 (3) 500 (4) 606 (5) 634
2003年(平成15年)問8 過去問解説
Δ-Δ結線1バンクとして使用するときの容量は、
$500×3=1500$[kVA]
V-V結線1バンクとして使用するときの容量は $P_V=\sqrt{3}P$ ですので、2バンクとして使用するときの容量は、
$2×\sqrt{3}×500=1732$[kVA]
よって、増加分は
$1732-1500=232$[kVA]
答え (2)
2004年(平成16年)問8
定格容量 100[kVA]、定格一次電圧 6.3[kV]で特性の等しい単相変圧器が2台あり、各変圧器の定格負荷時の負荷損は 1600[W]である。この変圧器2台をV-V結線し、一次電圧 6.3[kV]にて 90[kW]の三相平衡負荷をかけたとき、2台の変圧器の負荷損の合計値[W]として、最も近いのは次のうちどれか。ただし、負荷の力率は1とする。
(1) 324 (2) 423 (3) 648 (4) 864 (5) 1 440
2004年(平成16年)問8 過去問解説
負荷電力を単相変圧器として使用した場合の定格電流 $I_n$[A]は、
$I_n=\displaystyle\frac{P}{V_n}=\displaystyle\frac{100}{6.3}$[A]
この変圧器をV結線にして、90[kW]の三相平衡負荷をかけたときに流れる電流 $I_V$[A]は、
$I_V=\displaystyle\frac{90×10^3}{\sqrt{3}V_n}=\displaystyle\frac{90}{\sqrt{3}×6.3}$[A]
負荷損は電流の2乗に比例しますので、90[kW]の三相平衡負荷をかけたときの、変圧器1台あたりの負荷損を $P_l$[W]とすると、
${I_n}^2:{I_V}^2=1600:P_l$[W]
$P_l×\left(\displaystyle\frac{100}{6.3}\right)^2=1600×\left(\displaystyle\frac{90}{\sqrt{3}×6.3}\right)^2$
$P_l=432$[W]
2台の変圧器の負荷損の合計値[W]は、
$2P_l=2×432=864$[W]
答え (4)
2009年(平成21年)問7
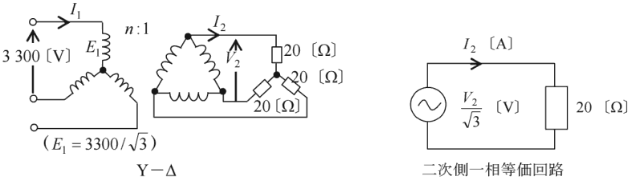
同一仕様である3台の単相変圧器の一次側を星形結線、二次側を三角結線にして、三相変圧器として使用する。 20[Ω]の抵抗器3個を星形に接続し、二次側に負荷として接続した。一次側 3300[V]の三相高圧母線に接続したところ、二次側の負荷電流は 12.7[A]であった。この単相変圧器の変圧比として、最も近いのは次のうちどれか。
ただし、変圧器の励磁電流、インピーダンス及び損失は無視するものとする。
(1) 4.33 (2) 7.50 (3) 13.0 (4) 22.5 (5) 39.0
2009年(平成21年)問7 過去問解説
二次側の線間電圧を $V_2$[V]、線電流を$I_2$[A]とすると、
$\displaystyle\frac{V_2}{\sqrt{3}}=I_2Z$
$V_2=\sqrt{3}×12.7×20=254\sqrt{3}$
一次側の相電圧 $E_1$[V]と、二次側の線間電圧を $V_2$[V]の関係は、変圧比を $n$ とすると、
$E_1=nV_2$
$n=\displaystyle\frac{\displaystyle\frac{3300}{\sqrt{3}}}{254\sqrt{3}}≒4.33$
答え (1)
2011年(平成23年)問8
下図は、三相変圧器の結線図である。
一次電圧に対して二次電圧の位相が 30[°]遅れとなる結線を次の(1)~(5)のうちから一つ選べ。
ただし、各一次・二次巻線間の極性は減極性であり、一次電圧の相順は U,V,W とする。
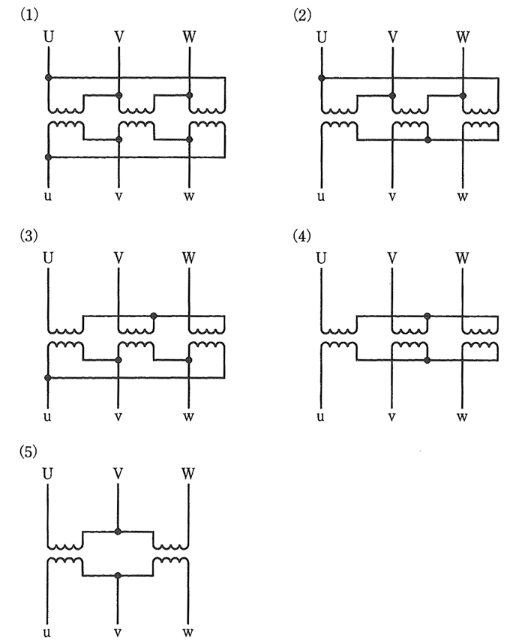
2011年(平成23年)問8 過去問解説
(1) Δ-Δ結線で同相。
(2) Δ-Y結線で30[°]進み
(3) Y-Δ結線で30[°]遅れ
(4) Y-Y結線で同相。
(5) V-V結線で同相。
結線図の接点の数に注目すると解りやすいです。
答え (3)
2015年(平成27年)問7
三相電源に接続する変圧器に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 変圧器鉄心の磁気飽和現象やヒステリシス現象は、正弦波の電圧、又は正弦波の磁束による励磁電流高調波の発生要因となる。変圧器のΔ結線は、励磁電流の第3次高調波を、巻線内を循環電流として流す働きを担っている。
- Δ結線がないY-Y結線の変圧器は、第3次高調波の流れる回路がないため、相電圧波形がひずみ、これが原因となって、近くの通信線に雑音などの障害を与える。
- Δ-Y結線又はY-Δ結線は、一次電圧と二次電圧との間に角変位又は位相変位と呼ばれる位相差45°がある。
- 三相の磁束が重畳して通る部分の鉄心を省略し、鉄心材料を少なく済ませている三相内鉄形変圧器は、単相変圧器3台に比べて据付け面積の縮小と軽量化が可能である。
- スコット結線変圧器は、三相3線式の電源を直交する二つの単相(二相)に変換し、大容量の単相負荷に電力を 供給する場合に用いる。三相のうち一相からの単相負荷電力供給は、三相電源に不平衡を生じるが、三相を二相に相数変換して二相側の負荷を平衡させると、三相側の不平衡を緩和できる。
2015年(平成27年)問7 過去問解説
Δ-Y結線又はY-Δ結線の位相差は30°です。したがって、(3)の記述が誤りです。
答え (3)
2015年(平成27年)問8
一次側の巻数が $N_1$、二次側の巻数が $N_2$ で製作された、同一仕様3台の単相変圧器がある。これらを用いて一次側をΔ結線、二次側をY結線として抵抗負荷、一次側に三相発電機を接続した。発電機を電圧 440 V、出力 100 kW、力率 1.0 で運転したところ、二次電流は三相平衡の 17.5 Aであった。この単相変圧器の巻数比 $N_1/N_2$ の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、変圧器の励磁電流、インピーダンス及び損失は無視するものとする。
(1) 0.13 (2) 0.23 (3) 0.40 (4) 4.3 (5) 7.5
2015年(平成27年)問8 過去問解説
二次側巻線の線間電圧を $V_{2l}$ 、二次側巻線の相電圧を $V_{2p}$ とすると、
$V_{2l}=\displaystyle\frac{P}{\sqrt{3}I_2}=\displaystyle\frac{100×10^3}{\sqrt{3}×17.5}$
$V_{2p}=\displaystyle\frac{V_{2l}}{\sqrt{3}}=\displaystyle\frac{100×10^3}{52.5}$
巻数比 $N_1/N_2$ は、
$\displaystyle\frac{N_1}{N_2}=\displaystyle\frac{E_1}{V_{2p}}=\displaystyle\frac{440}{\displaystyle\frac{100×10^3}{52.5}}=0.23$
答え (2)
2017年(平成29年)問7
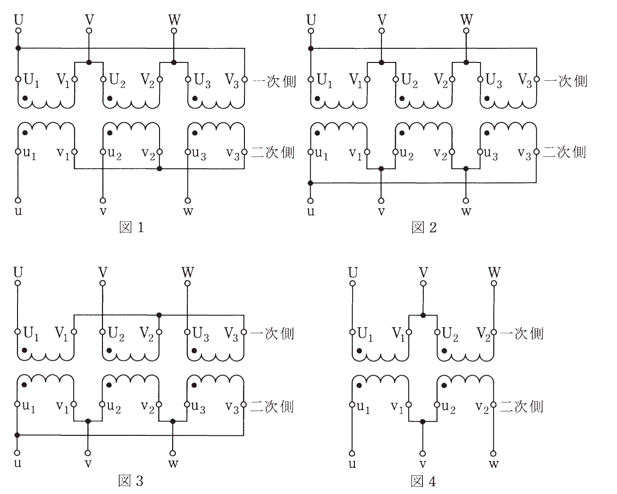
図1~3は、同じ定格の単相変圧器3台を用いた三相の変圧器であり、図4は、同じ定格の単相変圧器2台を用いたV結線三相変圧器である。各図の一次側電圧に対する二次側電圧の位相変位(角変位)の値 [rad] の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、各図において一次電圧の相順はU,V,Wとする。
| 図1 | 図2 | 図3 | 図4 | |
| (1) | 進み$\displaystyle\frac{π}{6}$ | 0 | 遅れ$\displaystyle\frac{π}{6}$ | 0 |
| (2) | 遅れ$\displaystyle\frac{π}{6}$ | 0 | 進み$\displaystyle\frac{π}{6}$ | 進み$\displaystyle\frac{π}{6}$ |
| (3) | 遅れ$\displaystyle\frac{π}{6}$ | 0 | 進み$\displaystyle\frac{π}{6}$ | 0 |
| (4) | 進み$\displaystyle\frac{π}{6}$ | 遅れ$\displaystyle\frac{π}{6}$ | 遅れ$\displaystyle\frac{π}{6}$ | 遅れ$\displaystyle\frac{π}{6}$ |
| (5) | 遅れ$\displaystyle\frac{π}{6}$ | 進み$\displaystyle\frac{π}{6}$ | 進み$\displaystyle\frac{π}{6}$ | 進み$\displaystyle\frac{π}{6}$ |
2017年(平成29年)問7 過去問解説
図1 Δ-Y結線で30[°]進み
図2 Δ-Δ結線で同相。
図3 Y-Δ結線で30[°]遅れ
図4 V-V結線で同相。
結線図の接点の数に注目すると解りやすいです。
答え (1)





