このページでは、三相同期発電機の特性について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された三相同期発電機の特性の過去問題の解き方も解説しています。
- 無負荷飽和曲線
- 短絡曲線
- 同期インピーダンスの計算
- 短絡比
- 外部特性曲線
- 電験三種-機械(同期機)過去問
- 1997年(平成9年)問2
- 1997年(平成9年)問2 過去問解説
- 1999年(平成11年)問4
- 1999年(平成11年)問4 過去問解説
- 2000年(平成12年)問2
- 2000年(平成12年)問2 過去問解説
- 2003年(平成15年)問4
- 2003年(平成15年)問4 過去問解説
- 2003年(平成15年)問5
- 2003年(平成15年)問5 過去問解説
- 2004年(平成16年)問5
- 2004年(平成16年)問5 過去問解説
- 2004年(平成16年)問6
- 2004年(平成16年)問6 過去問解説
- 2006年(平成18年)問3
- 2006年(平成18年)問3 過去問解説
- 2007年(平成19年)問5
- 2007年(平成19年)問5 過去問解説
- 2008年(平成20年)問4
- 2008年(平成20年)問4 過去問解説
- 2009年(平成21年)問5
- 2009年(平成21年)問5 過去問解説
- 2013年(平成25年)問6
- 2013年(平成25年)問6 過去問解説
- 2015年(平成27年)問4
- 2015年(平成27年)問4 過去問解説
- 2015年(平成27年)問5
- 2015年(平成27年)問5 過去問解説
- 2017年(平成29年)問5
- 2017年(平成29年)問5 過去問解説
無負荷飽和曲線
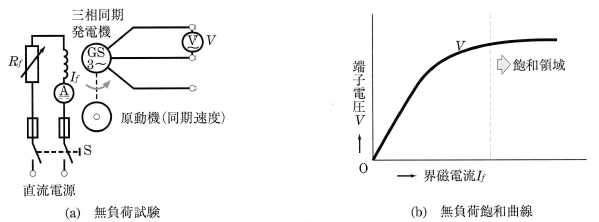
図1(a)は、無負荷試験の接続図です。無負荷試験は次のようにして行います。
同期発電機の端子は無負荷にして、原動機を運転します。同期発電機を定格回転速度として、以後、一定に保ちます。可変抵抗 $R_f$ を最大にして、直流電源のスイッチSを閉じ、磁極を励磁します。次に、界磁電流 $I_f$ をしだいに大きくし、$I_f$ と端子電圧 $V$ の関係を調べます。
いま、$I_f$ によって生じる磁束を $ϕ$[Wb]とすれば、端子電圧 $V$ は磁束 $ϕ$と比例関係にあります。また、$I_f$ と $ϕ$ との関係は、磁極鉄心による飽和特性になりますので、$I_f$ と $V$ との関係は、図1(b)に示すように飽和特性を示します。これを同期発電機の「無負荷飽和曲線」といいます。
短絡曲線
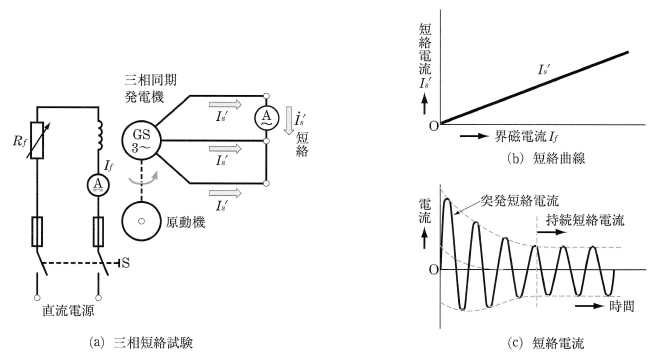
短絡曲線 図2(a)は、三相短絡試験の接続図です。同期発電機の端子を電流計で短絡し、定格回転速度で運転して、界磁電流 $I_f$[A]と電機子短絡電流 ${I_s}′$[A]の関係を調べると、図(b)に示すように、比例関係であることがわかります。この特性曲線を「短絡曲線」といいます。
短絡電流
同期発電機が、定格回転速度・定格電圧・無負荷で運転中、突発的に3相を短絡すると、図(c)に示す電流が流れます。
短絡直後は電機子反作用がないので、電流を制限するものは電機子抵抗と漏れリアクタンスだけであり、そのため非常に大きな過渡電流が流れます。この電流を突発短絡電流といいます。
短絡後数秒で電機子反作用が現れます。この場合の回路は誘導性ですので減磁作用となり、短絡電流は減少し、ついに電流は同期インピーダンスで制限されて一定の値になります。この電流を持続短絡電流といいます。
同期インピーダンスの計算
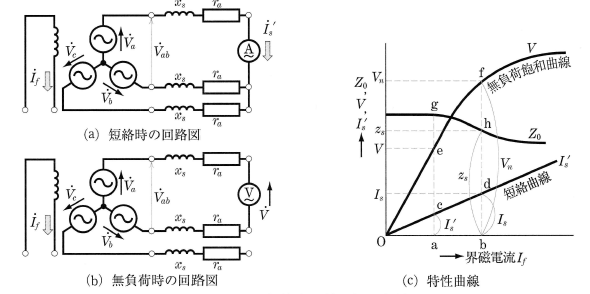
図3(a)から、相電圧 $V_a$[V]、線間電圧 $V_{ab}$[V]、短絡電流 ${I_s}’$[A]とすると、三相同期発電機の1相分のインピーダンス $Z_o$[Ω]は、次の式で表わすことができます。
$Z_o=\displaystyle\frac{V_a}{{I_s}’}=\displaystyle\frac{V_{ab}}{\sqrt{3}{I_s}’}$
しかし、$V_a$、$V_{ab}$[V]は、図(a)の回路からは測定できませんので $Z_o$ を求めることができません。そこで、無負荷試験により、短絡電流を流したときの界磁電流における電圧は測定できますので、この値を $V$[V]として、図(c)から、次の式を用いて $Z_o$ を求ます。
$Z_o=\displaystyle\frac{V_{ab}}{\sqrt{3}{I_s}’}=\displaystyle\frac{V}{\sqrt{3}{I_s}’}=\displaystyle\frac{\overline{ ea }}{\sqrt{3}・\overline{ ca }}=\overline{ ga }$
この $Z_o$ は、端子電圧 $V$[V]が飽和特性をもつため、一定になりません。そこで、$V$[V]が定格電圧 $V_n$[V]に等しいときの値を用い、それを同期インピーダンスと定義して、$Z_s$[Ω]で表します。つまり、図(c)から、次の式で表すことができます。
$Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}{I_s}’}=\displaystyle\frac{\overline{ fb}}{\sqrt{3}・\overline{ db }}=\overline{ hb }$
同期インピーダンスを求める式
$Z_s=\displaystyle\frac{V_n}{\sqrt{3}I_s}$
$Z_s$[Ω]:同期インピーダンス
$I_s$[A]:持続短絡電流
$\displaystyle\frac{V_n}{\sqrt{3}}$[V]:1相分の定格電圧
百分率同期インピーダンス
同期インピーダンスを Ω 単位で表さないで、% 単位で表す場合があります。これを「百分率インピーダンス」といい、$ \% Z_s$[%]で表し、次の式で定義します。
百分率同期インピーダンスを求める式
$ \%Z_s=\displaystyle\frac{Z_sI_n}{\displaystyle\frac{V_n}{\sqrt{3}}}×100=\displaystyle\frac{I_n}{I_s}×100$
$ \% Z_s$[%]:百分率同期インピーダンス
$Z_s$[Ω]:同期インピーダンス
$I_n$[A]:定格電流
$I_s$[A]:持続短絡電流
$V_n$[V]:定格電圧
ここで、$I_n$[A]は定格電流で、$I_s$[A]は無負荷で定格電圧を発生するときの界磁電流と等しい界磁電流における短絡電流です。
短絡比
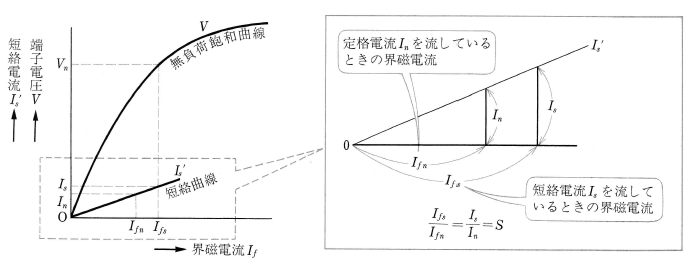
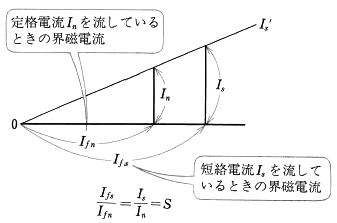
図4において定格電圧 $V_n$[V]が発生しているとき、突然三相短絡したときの持続短絡電流は、$I_s$[A]と等しくなります。この $I_s$が、定格電流 $I_n$[A]の何倍になるかを示す値を短絡比といいます。図4と百分率同期インピーダンスを求める式から、短絡比 $S$ は、次の式で表すことができます。
$S=\displaystyle\frac{I_{fs}}{I_{fn}}=\displaystyle\frac{I_s}{I_n}=\displaystyle\frac{100}{\%Z_s}$
短絡比の大きな同期発電機は、同期インピーダンスが小さく、短絡電流が大きいことがわかります。同期インピーダンスが小さいことは、電機子反作用が小さいことで、エアギャップが大きく、機械に余裕があり、電圧変動率も小さいですが、価格は高くなります。
一般に短絡比は0.6~1.2程度につくられます。たとえば、タービン発電機では0.6~1.0、水車発電機では0.9~1.2程度です。
短絡比が小さい場合の同期発電機の特徴
- 銅線が多く銅機械と呼ばれる
- インピーダンスが大きい
- 電圧変動率が大きい
- 安定度が悪い
- 小型にできる
短絡比が大きい場合の同期発電機の特徴
- 銅線が少なく鉄心部分が多いため鉄機械と呼ばれる
- インピーダンスが小さい
- 電圧変動率が小さい
- 安定度が良い
- 小型化できない
- 線路充電容量が大きい
短絡比を求める式
$S=\displaystyle\frac{I_{fs}}{I_{fn}}=\displaystyle\frac{I_s}{I_n}=\displaystyle\frac{100}{\%Z_s}$
$S$:短絡比
$I_{fs}$[A]:短絡電流を流しているときの界磁電流
$I_{fn}$[A]:定格電流を流しているときの界磁電流
$I_s$[A]:持続短絡電流
$I_n$[A]:定格電流
$ \% Z_s$[%]:百分率インピーダンス
同期発電機の定格電流を求める式
$I_n=\displaystyle\frac{P_n}{\sqrt{3}V_n}$
$I_n$[A]:定格電流
$P_n$[V・A]:定格電流を流しているときの界磁電流
$V_n$[A]:定格電圧
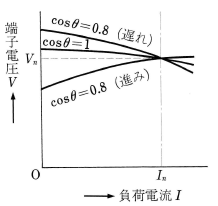
外部特性曲線
同期発電機の端子電圧 $V$[V]は、図5に示すように、負荷電流 $I$[A]や負荷力率によって変わります。界磁電流および負荷力率 $cos θ$ を一定に保ち、そのときの $I$ と $V$ の関係を示す曲線を「外部特性曲線」といいます。
電験三種-機械(同期機)過去問
1997年(平成9年)問2
定格出力 11000[KVA]、定格電圧 6600[V]の三相同期発電機がある。三相短絡電流 750[A]を流すのに必要な界磁電流が 54[A]である場合、この発電機の定格電流に等しい三相短絡電流を流すのに必要な界磁電流[A]の値として、正しいのは次のうちどれか。
(1) 69 (2) 96 (3) 120 (4) 208 (5) 289
1997年(平成9年)問2 過去問解説
定格電流を $I_n$[A]、 定格出力を $P_n$[W]、 定格電圧を $V_n$[V]とすると、
$I_n=\displaystyle\frac{P_n}{ \sqrt{3}V_n}=\displaystyle\frac{11000×10^3}{\sqrt{3}×6600}=963$[A]
定格時の界磁電流を $I_{fn}$[A]、三相短絡電流を $I_s$[A]、短絡時の界磁電流を $I_{fn}$[A]、短絡比を $S$ とすると、
$S=\displaystyle\frac{I_{fs}}{I_{fn}}=\displaystyle\frac{I_s}{I_n}$
$\displaystyle\frac{54}{I_{fn}}=\displaystyle\frac{750}{963}$
$I_{fn}=\displaystyle\frac{963}{750}×54=69$[A]

答え (1)
1999年(平成11年)問4
定格電圧 3300[V]、定格電流 210[A]の三相同期発電機がある。この発電機の電機子端子を開放した状態で界磁電流を増加していくと、120[A]に達したとき定格電圧が発生した。次に、その電機子端子を短絡して同じ 120[A]の界磁を与えると、短絡電流は定格電流の1.4倍であった。この発電機の同期インピーダンス[Ω]の値として、正しいのは次のうちどれか。
(1) 0.76 (2) 1.6 (3) 3.7 (4) 6.5 (5) 11.2
1999年(平成11年)問4 過去問解説
定格電圧を $V_n$[V]、短絡電流 ${I_s}’$[A]とすると、同期インピーダンス $Z_s$[Ω]は、
$ Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}{I_s}’}= \displaystyle\frac{3300}{\sqrt{3}×210×1.4}=6.5 $[Ω]
答え (4)
2000年(平成12年)問2
定格電圧 6,000[V]も定格電流 500[A]の三相同期発電機がある。無負荷で定格電圧を発生させるのに必要な界磁電流は 88[A]であり、三相短絡試験における界磁電流Ifと電機子電流Isとの関係は図のとおりである。
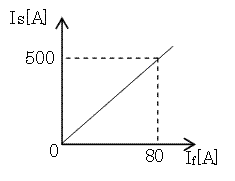
この同期発電機の短絡比の値として、正しいのは次のうちどれか。
(1) 0.91 (2) 1.10 (3) 1.21 (4) 5.68 (5) 6.25
2000年(平成12年)問2 過去問解説
定格時の界磁電流を $I_{fn}$[A]、短絡時の界磁電流を $I_{fs}$[A]とすると、短絡比 $S$ は、
$S=\displaystyle\frac{I_{fs}}{I_{fn}}=\displaystyle\frac{80}{88}=0.91$
答え (1)
2003年(平成15年)問4
三相同期発電機があり、無負荷で端子電圧(線間) 15.2[kV]を発生させるのに必要な界磁電流は 500[A]である。この界磁電流を 100[A]にして短絡試験を行ったとき、短絡電流 860[A]が流れた。界磁電流 500[A]のとき、この発電機の同期インピーダンス[Ω]の値として最も近いものは次のうちどれか。
(1) 0.55 (2) 2.04 (3) 3.53 (4) 6.86 (5) 10.2
2003年(平成15年)問4 過去問解説
界磁電流を $I_{f}$[A]のときの短絡電流を $I_s$[A]、界磁電流を $I_{f}’$[A]のときの短絡電流を ${I_s}’$[A]とすると、短絡比 $S$ は一定ですので、
$S=\displaystyle\frac{I_{f}’}{I_{f}}=\displaystyle\frac{{I_s}’}{I_s}$
${I_s}’=I_s×\displaystyle\frac{I_{f}’}{I_{f}}=860×\displaystyle\frac{500}{100}=4300$[A]
同期インピーダンス $Z_s$[Ω]は、
$Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}{I_s}’}=\displaystyle\frac{15.2×10^3}{\sqrt{3}×4300}≒2.04$
答え (2)
2003年(平成15年)問5
三相同期発電機の短絡比に関する記述として、誤っているのは次のうちどれか。
- 短絡比を小さくすると、発電機の外形寸法がちいさくなる。
- 短絡比を小さくすると、発電機の安定度が悪くなる。
- 短絡比を小さくすると、電圧変動率が小さくなる。
- 短絡比を小さい発電機は、銅機械と呼ばれる。
- 短絡比を小さい発電機は、同期インピーダンスが大きい。
2003年(平成15年)問5 過去問解説
短絡比の小さい機械は同期インピーダンスが大きく、電機子反作用が大くなります。電機子反作用が大きいのはギャップが小さく、回転子の磁極の磁力が電機子の起磁力に比べて小さいことになり、界磁の材料である銅や鉄がきりつめてあることになります。短絡比の小さい同期機は、軽くて安価ですが、特性上の余裕はないことになり、電圧変動率も大きくなります。したがって、(3)の記述が誤りです。
答え (3)
2004年(平成16年)問5
三相同期発電機があり、定格出力は 5000[kVA]、定格電圧は 6.6[kV]、短絡比は 1.1 である。この発電機の同期インピーダンス[Ω]の値として、最も近いのは次のうちどれか。
(1) 2.64 (2) 4.57 (3) 7.92 (4) 13.7 (5) 23.8
2004年(平成16年)問5 過去問解説
定格出力を $P_n$[W]、 定格電流を $I_n$[A]、 定格電圧を $P_n$[V]とすると、
$I_n=\displaystyle\frac{P_n}{ \sqrt{3}V_n}=\displaystyle\frac{5000×10^3}{\sqrt{3}×6600}≒437.4$[A]
三相短絡電流を $I_s$[A]、短絡比を $S$ 、同期インピーダンスを $ Z_s $ とすると、 百分率同期インピーダンス $ \%Z_s $ は、
$ \%Z_s=\displaystyle\frac{Z_sI_n}{\displaystyle\frac{V_n}{\sqrt{3}}}×100$
短絡比を $S$ とすると、
$S=\displaystyle\frac{100}{\%Z_s}$
$ \%Z_s=\displaystyle\frac{100}{S}$
したがって、
$\displaystyle\frac{Z_sI_n}{\displaystyle\frac{V_n}{\sqrt{3}}}×100= \displaystyle\frac{100}{S}$
$Z_s=\displaystyle\frac{1}{S}×\displaystyle\frac{V_n}{\sqrt{3}I_n}=\displaystyle\frac{1}{1.1}×\displaystyle\frac{6600}{\sqrt{3}×437.4}≒7.92$[Ω]
答え (3)
2004年(平成16年)問6
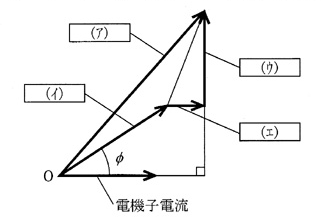
図は、三相同期発電機が負荷を負って遅れ力率φで運転しているときの、電機子巻線1相についてのベクトル図である。ベクトル(ア),(イ),(ウ)及び(エ)が表わすものとして、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 誘導起電力 | 端子電圧 | 同期リアクタンス降下 | 電機子巻線抵抗降下 |
| (2) | 誘導起電力 | 端子電圧 | 電機子巻線抵抗降下 | 同期インピーダンス降下 |
| (3) | 端子電圧 | 誘導起電力 | 同期リアクタンス降下 | 電機子巻線抵抗降下 |
| (4) | 誘導起電力 | 端子電圧 | 同期インピーダンス降下 | 同期リアクタンス降下 |
| (5) | 端子電圧 | 誘導起電力 | 電機子巻線抵抗降下 | 同期リアクタンス降下 |
2004年(平成16年)問6 過去問解説
- 最大のベクトルなので、誘導起電力です。
- 誘導起電力から電機子巻線電圧降下とリアクタンスによる電圧降下を引いたものなので、端子電圧です。
- 電機子巻線電圧降下より90°進んだベクトルになるので、リアクタンスによる電圧降下です。
- 電機子電流と同相なので、電機子巻線電圧降下です。
答え (1)
2006年(平成18年)問3
定格出力 5[MVA]、定格電圧 6.6[KV]、定格回転速度 1,800[min-1]の三相同期発電機がある。この発電機の同期インピーダンスが 7.26[Ω]のとき、短絡比の値として正しいのは次のうちどれか。
(1) 0.14 (2) 0.83 (3) 1.0 (4) 1.2 (5) 1.5
2006年(平成18年)問3 過去問解説
定格出力を $P_n$[W]、 定格電流を $I_n$[A]、 定格電圧を $P_n$[V]とすると、
$I_n=\displaystyle\frac{P_n}{ \sqrt{3}V_n}=\displaystyle\frac{5000×10^3}{\sqrt{3}×6600}≒437.4$[A]
同期インピーダンスを $ Z_s $[Ω]とすると、短絡電流 $I_s$[A]は、
$Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}{I_s}}$
$7.26=\displaystyle\frac{6600}{\sqrt{3}{I_s}}$
$I_s=\displaystyle\frac{6600}{\sqrt{3}×{7.26}}≒524.9$
短絡比を $S$ は
$S=\displaystyle\frac{I_s}{I_n}=\displaystyle\frac{524.9}{437.4}≒1.2$
答え (4)
2007年(平成19年)問5
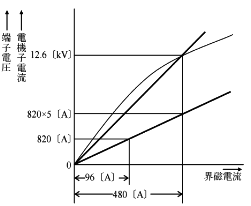
定格速度、励磁電流 480[A]、無負荷で運転している三相同期発電機がある。この状態で、無負荷電圧(線間)を測ると 12600[V]であった。つぎに、96[A]の励磁電流を流して短絡試験を実施したところ、短絡電流は 820[A]であった。この同期発電機の同期インピーダンスとして最も近いのは次のうちどれか。
ただし、磁気飽和は無視できるものとする。
(1) 1.77 (2) 3.07 (3) 15.4 (4) 44.4 (5) 76.8
2007年(平成19年)問5 過去問解説
励磁電流 $I_{f1}=96$[A]のときの短絡電流は $I_{s1}=820$[A]ですので、励磁電流 $I_{f2}=480$[A]のときの短絡電流を $I_{s2}$[A]とすると、
$I_{s2}=I_{s1}×\displaystyle\frac{I_{f2}}{I_{f1}}=820×\displaystyle\frac{480}{96}=4100$[A]
定格電圧を $V_n=12600$[V]、短絡電流 $I_{s2}=4100$[A]のときの、同期インピーダンス $Z_s$[Ω]は、
$Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}I_{s2}}=\displaystyle\frac{12600}{\sqrt{3}×4100}≒1.77 $[Ω]
答え (1)
2008年(平成20年)問4
次の文章は、三相同期発電機の特性曲線に関する記述である。
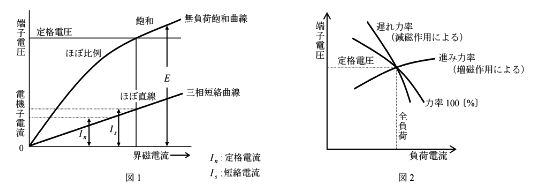
- 無負荷飽和曲線は、同期発電機を( ア )で無負荷で運転し、界磁電流を零から徐々に増加させたときの端子電圧と界磁電流との関係を表したものである。端子電圧は、界磁電流が小さい範囲では界磁電流に( イ )するが、界磁電流がさらに増加すると、飽和特性を示す。
- 短絡曲線は、同期発電機の電機子巻線の三相の出力端子を短絡し、定格速度で運転して、界磁電流を零から徐々に増加させたときの短絡電流と界磁電流との関係を表したものである。この曲線は( ウ )になる。
- 外部特性曲線は、同期発電機を定格速度で運転し、( エ )を一定に保って、( オ )を一定にして負荷電流を変化させた場合の端子電圧と負荷電流との関係を表したものである。この曲線は( オ )によって形が変わる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる語句とし正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 定格速度 | ほぼ比例 | ほぼ双曲線 | 界磁電流 | 残留磁気 |
| (2) | 定格電圧 | ほぼ比例 | ほぼ直線 | 電機子電流 | 負荷力率 |
| (3) | 定格速度 | ほぼ反比例 | ほぼ双曲線 | 電機子電流 | 残留磁気 |
| (4) | 定格速度 | ほぼ比例 | ほぼ直線 | 界磁電流 | 負荷力率 |
| (5) | 定格電圧 | ほぼ反比例 | ほぼ双曲線 | 界磁電流 | 残留磁気 |
2008年(平成20年)問4 過去問解説
- 無負荷飽和曲線は、同期発電機を( 定格速度 )で無負荷で運転し、界磁電流を零から徐々に増加させたときの端子電圧と界磁電流との関係を表したものである。端子電圧は、界磁電流が小さい範囲では界磁電流に( ほぼ比例 )するが、界磁電流がさらに増加すると、飽和特性を示す。
- 短絡曲線は、同期発電機の電機子巻線の三相の出力端子を短絡し、定格速度で運転して、界磁電流を零から徐々に増加させたときの短絡電流と界磁電流との関係を表したものである。この曲線は( ほぼ直線 )になる。
- 外部特性曲線は、同期発電機を定格速度で運転し、( 界磁電流 )を一定に保って、( 負荷力率 )を一定にして負荷電流を変化させた場合の端子電圧と負荷電流との関係を表したものである。この曲線は( 負荷力率 )によって形が変わる。
答え (4)
2009年(平成21年)問5
定格出力 5000[kVA]、定格電圧 6600[V]の三相同期発電機がある。 無負荷時に定格電圧となる励磁電流に対する三相短絡電流(持続短絡電流)は、500[A]であった。この同期発電機の短絡比の値として、最も近いのは次のうちどれか。
(1) 0.660 (2) 0.875 (3) 1.00 (4) 1.14 (5) 1.52
2009年(平成21年)問5 過去問解説
定格電流を $I_n$[A]、 定格出力を $P_n$[W]、 定格電圧を $V_n$[V]とすると、
$I_n=\displaystyle\frac{P_n}{ \sqrt{3}V_n}=\displaystyle\frac{5000×10^3}{\sqrt{3}×6600}≒437$[A]
三相短絡電流を $I_s$[A]、短絡比を $S$ とすると、
$S=\displaystyle\frac{I_s}{I_n}$
$S=\displaystyle\frac{500}{437}≒1.14$
答え (4)
2013年(平成25年)問6
定格電圧 6.6[kV]、定格電流 1050[A]の三相同期発電機がある。この発電機の短絡比は 1.25 である。この発電機の同期インピーダンス[Ω]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.80 (2) 2.90 (3) 4.54 (4) 5.03 (5) 7.86
2013年(平成25年)問6 過去問解説
定格電流を $I_n$[A]、三相短絡電流を $I_s$[A]、短絡比を $S$ とすると、
$S=\displaystyle\frac{I_s}{I_n}$
$I_s=I_n×S$
定格電圧を $V_n$[V]とすると、同期インピーダンス $Z_s$[Ω]は、
$Z_s=\displaystyle\frac{V_{n}}{\sqrt{3}I_{s}}$
$=\displaystyle\frac{V_{n}}{\sqrt{3}I_n×S}$
$=\displaystyle\frac{6600}{\sqrt{3}×1050×1.25}≒2.90 $[Ω]
答え (2)
2015年(平成27年)問4
定格電圧、定格電流、力率 1.0 で運転中の三相同期発電機がある。百分率同期インピーダンスは 85% である。励磁電流を変えないで、無負荷にしたとき、この発電機の端子電圧は定格電圧の何倍になるか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、電機子巻線抵抗と磁気飽和は無視できるものとする。
(1) 1.0 (2) 1.1 (3) 1.2 (4) 1.3 (5) 1.4
2015年(平成27年)問4 過去問解説
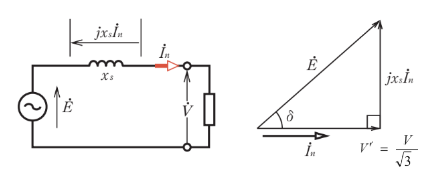
三相同期発電機の1相分の等価回路とベクトル図を示します。
百分率同期インピーダンスを1相分で考えると、
$ \%Z_s=\displaystyle\frac{x_sI_n}{ \sqrt {3}V}=85$
ベクトル図より、
$E=\sqrt{(\displaystyle\frac{ V }{\sqrt {3}})^2+(x_sI_n)^2}$
1相分の起電力と負荷電圧の比は、
$\displaystyle\frac{E}{V}=\displaystyle\frac{\sqrt{(\displaystyle\frac{ V }{\sqrt {3}})^2+(x_sI_n)^2}}{V}$
$=\sqrt{1^2+(\displaystyle\frac{x_sI_n}{\sqrt {3}V})^2} $
$=\sqrt{1^2+85^2}≒1.3 $
答え (4)
2015年(平成27年)問5
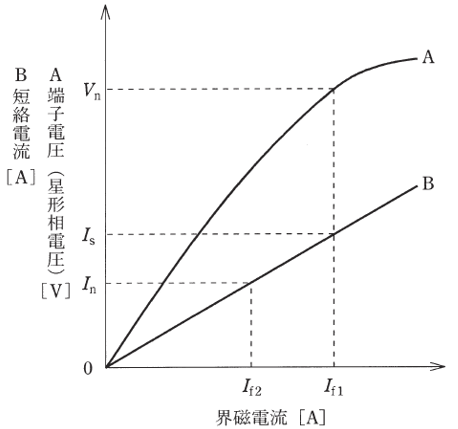
図は、同期発電機の無負荷飽和曲線(A)と短絡曲線(B)を示している。図中で Vn[V]は端子電圧(星形相電圧)の定格値、In[A]は定格電流、Is[A]は無負荷で定格電圧を発生するときの界磁電流と等しい界磁電流における短絡電流である。この発電機の百分率同期インピーダンス ZS[%]を示す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
- $\displaystyle\frac{I_s}{I_n}×100$
- $\displaystyle\frac{V_n}{I_n}×100$
- $\displaystyle\frac{I_n}{I_{f2}}×100$
- $\displaystyle\frac{V_n}{I_{f1}}×100$
- $\displaystyle\frac{I_{f2}}{I_{f1}}×100$
2015年(平成27年)問5 過去問解説
短絡比を $S$ とすると、
$S=\displaystyle\frac{I_{f1}}{I_{f2}}=\displaystyle\frac{I_s}{I_n}$
百分率同期インピーダンス%ZS[%]は、
$ \%Z_s=\displaystyle\frac{I_n}{I_s}×100=\displaystyle\frac{I_{f2}}{I_{f1}}×100$
答え (5)
2017年(平成29年)問5
定格出力 10MV・A、定格電圧 6.6kV、百分率同期インピーダンス80%の三相同期発電機がある。三相短絡電流 700Aを流すのに必要な界磁電流が 50Aである場合、この発電機の定格電圧に等しい無負荷端子電圧を発生させるのに必要な界磁電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、百分率同期インピーダンスの抵抗分は無視できるものとする。
(1) 50.0 (2) 62.5 (3) 78.1 (4) 86.6 (5) 135.3
2017年(平成29年)問5 過去問解説
定格電流を $I_n$[A]、 定格出力を $P_n$[W]、 定格電圧を $V_n$[V]とすると、
$I_n=\displaystyle\frac{P_n}{ \sqrt{3}V_n}=\displaystyle\frac{10×10^6}{\sqrt{3}×6600}≒857.8$[A]
三相短絡電流を $I_s$[A]とすると、百分率同期インピーダンスが 80% ですので、
$ \%Z_s=\displaystyle\frac{I_n}{I_s}×100=\displaystyle\frac{857.8}{I_s}×100=80$
$I_s=875.8×\displaystyle\frac{100}{80}≒1094.8$[A]
したがって、求める界磁電流 $I_f$[A]は、
$1094.8:700=I_f:50$
$I_f≒78.1$[A]
答え (3)





