このページでは、ブロック線図と伝達関数について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目の試験で実際に出題された、ブロック線図と伝達関数についての過去問題も解説しています。
- ブロック線図と伝達関数
- ラプラス変換
- 伝達関数の計算方法
- 電験三種-機械(自動制御)過去問
- 1997年(平成9年)問13
- 1997年(平成9年)問13 過去問解説
- 1998年(平成10年)問9
- 1998年(平成10年)問9 過去問解説
- 2000年(平成12年)問13
- 2000年(平成12年)問13 過去問解説
- 2002年(平成14年)問10
- 2002年(平成14年)問10 過去問解説
- 2004年(平成16年)問17
- 2004年(平成16年)問17 過去問解説
- 2005年(平成17年)問13
- 2005年(平成17年)問13 過去問解説
- 2006年(平成18年)問13
- 2006年(平成18年)問13 過去問解説
- 2007年(平成19年)問17
- 2007年(平成19年)問17 過去問解説
- 2008年(平成20年)問17
- 2008年(平成20年)問17 過去問解説
- 2010年(平成22年)問13
- 2010年(平成22年)問13 過去問解説
- 2013年(平成25年)問13
- 2013年(平成25年)問13 過去問解説
- 2015年(平成27年)問17
- 2015年(平成27年)問17 過去問解説
ブロック線図と伝達関数
ブロック線図は、制御系の信号の伝わり方を、図式的に表現する方法です。電気回路図がエネルギーの伝わり方も表現しているのに対して、ブロック線図は信号の伝わり方だけを示した信号伝達の系統図といえます。
例えば、入力を $X$、出力を $Y$ とすると、$X$ と $Y$ の関係は $Y=GX$ で表すことができます。この $G$ を信号の伝達要素と考えれば、$Y=GX$ の関係は、図のように線と矢印とブロック(枠)で表すことができます。尚、$G$ を伝達関数といいます。
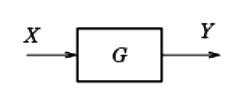
ブロック線図の構成
ブロック線図は次の図のように直線と矢印、白丸(○)、黒丸(●)、+−の符号、四角の枠(ブロック)から成り立っています。
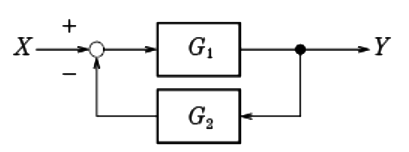
- 信号線
信号の経路を直線で、信号の伝達方法を矢印で表します。
- 引出点
一つの信号を2系統に分岐して取り出すことを示し、黒丸●で表します。信号の量は減少しません。
- 加合せ点(差引き点)
二つの信号が加え合わされ(差し引かれ)た代数和を作ることを示します。白丸○で表します。 - +−符号
加え合わされる信号を+−符号で表します。フィードバック信号は−符号です。
- 伝達要素
信号を受け取り、ほかの信号に変換する要素を示し、四角の枠で表します。通常この中に伝達関数を記入します。
伝達関数
伝達関数とは、システムへの入力と出力の関係を表現したもので、伝達関数を $G(s)$、入力を $X(s)$、出力を $Y(s)$ としたとき、$G(s)=\displaystyle\frac{Y(s)}{X(s)}$ と定義されます。
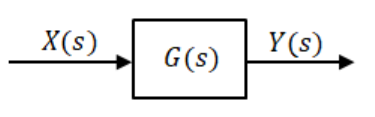
伝達関数は $G(s)$ のように 複素数 $s$ の関数で表されます。私たちが「入出力の関係を表す関数」といって直感的に理解しやすいのは、$Y(t)=G(t)・X(t)$ のような、時間 $t$ の関数です。しかし、伝達関数が扱う「領域」は、「時間領域」ではなく「s領域」です。
s領域とは、複素数の世界を表したもので、時間領域を写像したものです。ここでいう写像とは、時間 $t$ の関数のまま計算すると、とても複雑になるような計算式を、複素数 $s$ の関数に変換して、計算を簡単にする方法です。その変換に使うのは、「ラプラス変換」という計算方法です。
周波数伝達関数
正弦波入力に対する周波数特性を表す伝達関数を周波数伝達関数といいます。周波数伝達関数は、伝達関数の複素数 $s$ の関数の代わりに $jω$ で表します。
周波数伝達関数を $G(jω)$、入力を $X(jω)$、出力を $Y(jω)$ としたとき、$G(jω)=\displaystyle\frac{Y(jω)}{X(jω)}$ と定義されます。
ブロック線図の等価変換の計算
個々の制御要素(伝達関数)を等価変換してひとつの制御要素にする事で制御ブロックをシンプルに表現できます。これを等価変換といい、制御系の本質は変わりません。
直列接続
$Y=XG1G2$
$G=\displaystyle\frac{Y}{X}=G1・G2$
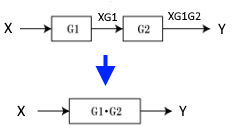
並列接続
$Y=XG1+XG2$
$G=\displaystyle\frac{Y}{X}=G1+G2$
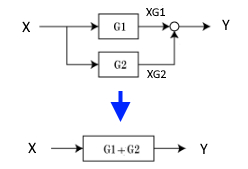
フィードバック信号
$Y=(X-Y)G$
$Y(1+G)=XG$
$G=\displaystyle\frac{Y}{X}=\displaystyle\frac{G}{1+G}$
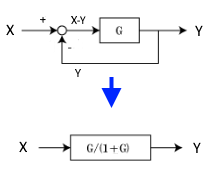
等価変換まとめ
ラプラス変換
ラプラス変換は、時間 t の関数と複素数 s を行き来するための計算方法です。ラプラス変換の定義は、時間 t の関数
時間 t の関数を f(t) とすると
$F(s)=\displaystyle \int_{0}^{ \infty } f(t)・e^{-st}・dt$
のように与えられます.この式は時間 t の関数 f(t) に $e^{-st}$ を掛け合わせたものについて t=0 から ∞ までを積分することで t の関数を s の関数 F(s) に変換するものです。この変換をラプラス変換といいます。式中の s はラプラス演算子といい s>0 で複素数も取り得ます。尚、ラプラス変換を数式記号を用いて示す場合は次のように記します。
$F(s)=$ℒ[$f(t)$]
ラプラス変換された関数 F(s) を時間関数 f(t) に再び変換することをラプラス逆変換といいます.ラプラス逆変換を数式記号を用いて示す場合は次のように記します。
$f(t)=$ℒ-1[$F(s)$]
伝達関数の計算方法
伝達関数 G(s) の求め方は、まずは制御システムの微分方程式を考えます。考えた微分方程式をラプラス変換して、 s 関数で表現します。そして、出力と入力の比を取ると伝達関数 G(s) を求めることができます。
図のようなL-R回路の伝達関数 G(s) を求めてみます。
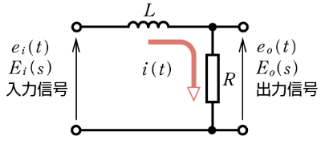
まず、回路方程式(微分方程式)をつくります。
入力信号:$e_i(t)=L\displaystyle\frac{di(t)}{dt}+Ri(t)$
出力信号:$e_o(t)=Ri(t)$
両辺をラプラス変換します。
入力信号:$E_i(s)=LsI(s)+RI(s)$
出力信号:$E_o(t)=RI(s)$
伝達関数 G(s) は、出力と入力の比ですので、
$G(s)=\displaystyle\frac{E_o(t)}{E_i(s)}$
$=\displaystyle\frac{RI(s)}{LsI(s)+RI(s)}$
$=\displaystyle\frac{R}{Ls+R}$
$=\displaystyle\frac{1}{s\displaystyle\frac{L}{R}+1}$
$=\displaystyle\frac{1}{1+sT}$($\displaystyle\frac{L}{R}=T$:時定数)
伝達関数 $G(s)=\displaystyle\frac{E_o(t)}{E_i(s)}=\displaystyle\frac{出力信号}{入力信号}$
電験三種-機械(自動制御)過去問
1997年(平成9年)問13
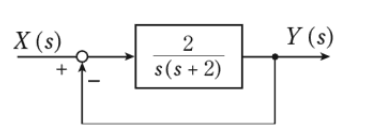
図のようなフィードバック制御系がある。この系の伝達関数を
$\displaystyle\frac{Y(s)}{X(s)}=\displaystyle\frac{{ω_n}^2}{s^2+2ζω_ns+{ω_n}^2}$
と表した場合、固有周波数 $ω_n$ 及び減衰係数 $ζ$ の値として、正しいものを組み合わせたのは次のうちどれか。
- $ω_n=2$ $ζ=0.5$
- $ω_n=\sqrt{2}$ $ζ=\displaystyle\frac{1}{\sqrt{2}}$
- $ω_n=1$ $ζ=1$
- $ω_n=\sqrt{2}$ $ζ=\sqrt{2}$
- $ω_n=2$ $ζ=1$
1997年(平成9年)問13 過去問解説
入力 $X$ と増幅回路の出力 $Y$ がフィードバックする回路では、

$Y=(X-Y)G=XG-YG$
$Y(1+G)=XG$
$\displaystyle\frac{Y}{X}=\displaystyle\frac{G}{1+G}=利得$
題意より
$\displaystyle\frac{Y(s)}{X(s)}=\displaystyle\frac{G(s)}{1+G(s)}=\displaystyle\frac{\displaystyle\frac{2}{s(s+2)}}{1+\displaystyle\frac{2}{s(s+2)}}=\displaystyle\frac{2}{s^2+2s+2}$
よって、$2={ω_n}^2$,$2s=2ζω_ns$ となりますので、
$ω_n=\sqrt{2}$ $ζ=\displaystyle\frac{1}{\sqrt{2}}$
答え (2)
1998年(平成10年)問9
自動制御系における( ア )は、一般に負になっているので、不安定になることはないように思われる。しかし、一般の制御系は、周波数が増大するにつれて位相が遅れる特性をもっており、一巡周波数伝達関数の位相の遅れが( イ )になる周波数に対しては( ア )は正になる。制御系にはあらゆる周波数成分をもった雑音が存在するので、その周波数における一巡周波数伝播関数のゲインが( ウ )になると、その周波数成分の振幅が増大していって、ついには不安定になる。これがナイキスト安定判別法の大まかな解釈である。
上記の記述中の空白箇所(ア), (イ)及び(ウ)に記入する字句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | フィードバック | 90° | 2以上 |
| (2) | フィードフォワード | 90° | 1以上 |
| (3) | フィードバック | 180° | 1以上 |
| (4) | フィードフォワード | 180° | 1以下 |
| (5) | フィードバック | 90° | 2以下 |
1998年(平成10年)問9 過去問解説
自動制御系における( フィードバック )は、一般に負になっているので、不安定になることはないように思われる。しかし、一般の制御系は、周波数が増大するにつれて位相が遅れる特性をもっており、一巡周波数伝達関数の位相の遅れが( 180° )になる周波数に対しては( ア )は正になる。制御系にはあらゆる周波数成分をもった雑音が存在するので、その周波数における一巡周波数伝播関数のゲインが( 1以上 )になると、その周波数成分の振幅が増大していって、ついには不安定になる。これがナイキスト安定判別法の大まかな解釈である。
一般に用いられる自動制御には負帰還フィードバック方式が用いられますが、周波数が180°以上遅れると、利得が正(-(-1)=+1)となって、正帰還と同じ働きをするため不安定になります。また、利得が1以上になると振幅が増大して、不安定な動作をします。
しかし、例えば自動車が高速で走行中に前の車両が急に停止した場合、外乱が大きいので、とっさにブレーキを踏まなければなりません(フィードフォワード制御)。
答え (3)
2000年(平成12年)問13
次式で表される二次振動要素の周波数伝達関数の系がある。
$G(jω)=\displaystyle\frac{4}{(jω)^2+1.6(jω)+4}$
この周波数伝達関数について、次の(a)及び(b)に答えよ。
(a) 位相が90°遅れるときの角周波数 $ω$[rad/s]の値として、正しいのは次のうちどれか。
(1) 1 (2) 2 (3) 3 (4) 4 (5) 5
(b) ベクトル軌跡が虚軸を切る点のゲイン $|G(jω)|$ の値として、正しいのは次のうちどれか。
(1) 0.5 (2) 0.75 (3) 1.00 (4) 1.25 (5) 2.5
2000年(平成12年)問13 過去問解説
(a) 位相が90°遅れるときの角周波数 $ω$[rad/s]は、周波数伝達関数 $G(jω)$ の分母の実数部が $0$ になるときです。
$G(jω)=\displaystyle\frac{4}{(jω)^2+1.6(jω)+4}=\displaystyle\frac{4}{(4-ω^2)+j1.6ω}$
したがって、
$4-ω^2=0$
$ω=2$[rad/s]
答え (2)
(b) ベクトル軌跡が虚軸を切る点のゲイン $G(jω)$ は、虚数部のみになりますので、そのときの角周波数は、$ω=2$[rad/s]となります。ゲインの絶対値 $|G(jω)|$ は、
$|G(jω)|=\displaystyle\frac{4}{1.6×2}=1.25$
答え (4)
2002年(平成14年)問10
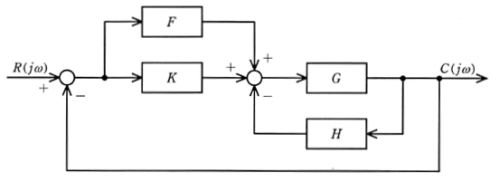
図のようなブロック線図で示す制御系がある。入力信号 $R(jω)$ と出力信号 $C(jω)$ 間の合成の周波数伝達関数 $\displaystyle\frac{C(jω)}{R(jω)}$ を示す式として、正しいのは次のうちどれか。
- $\displaystyle\frac{G(F+K)}{1+G(H+F+K)}$
- $\displaystyle\frac{G(F-K)}{1+G(H+F-K)}$
- $\displaystyle\frac{G(F+K)}{1-G(H+F+K)}$
- $\displaystyle\frac{GH(F+K)}{1-GH(H+F+K)}$
- $\displaystyle\frac{GHK}{1+G(H+F+K)}$
2002年(平成14年)問10 過去問解説
まずは次のフィードバック部分の伝達関数を求めます。
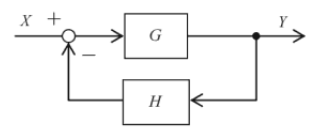
$Y=(X-YH)G=XG-YHG$
$Y(1+HG)=XG$
$\displaystyle\frac{Y}{X}=\displaystyle\frac{G}{1+HG}$
題意のブロック図は次のように置きかえることができます。
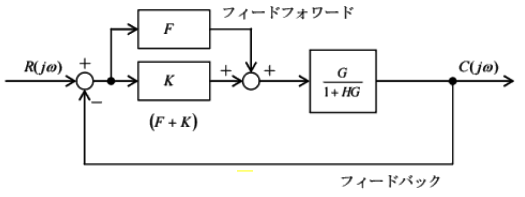
したがって、
$G(jω)=\{R(jω)-C(jω)\}×(F+K)×\displaystyle\frac{G}{1+HG}$
$G(jω)\left\{1+\displaystyle\frac{(F+K)G}{1+HG}\right\}=R(jω)\left\{\displaystyle\frac{(F+K)G}{1+HG}\right\}$
$\displaystyle\frac{C(jω)}{R(jω)}=\displaystyle\frac{G(F+K)}{1+G(H+F+K)}$
答え (1)
2004年(平成16年)問17
開ループ周波数伝達関数 $G(jω)$ が
$G(jω)=\displaystyle\frac{10}{jω(1+j0.2ω)}$
で表わされる制御系がある。
変数 $ω$ を $0$ から $∞$ まで変化させたとき、$G(jω)$ の値は図のようなベクトル軌跡となる。次の(a)及び(b)に答えよ。
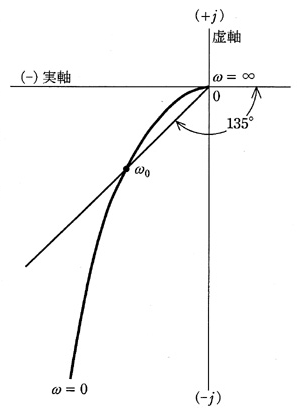
(a) この系の位相角が $-135°$ となる角周波数 $ω_0$[rad/s]の値として、正しいのは次のうちどれか。
(1) 1 (2) 2 (3) 5 (4) 8 (5) 10
(b) この $ω_0$[rad/s]におけるゲイン $|G(jω)|$ の値として、最も近いのは次のうちどれか。
(1) 0.45 (2) 1.41 (3) 3.53 (4) 4.62 (5) 9.78
2004年(平成16年)問17 過去問解説
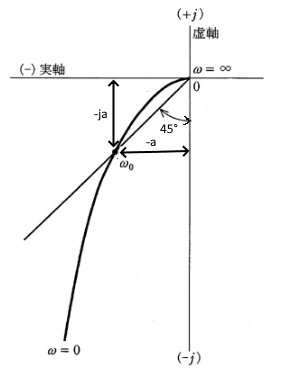
(a) 題意より、角周波数 $ω_0$[rad/s]における開ループ周波数伝達関数 $G(jω)$ の実部と虚部が等しくなりますので、$G(jω)$ の分母は、
$jω(1+j0.2ω)=jω-0.2ω^2$
となりますので、$ω_0=0.2ω^2$ となるのは、
$1=0.2ω_0$
$ω_0=5$[rad/s]
答え (3)
(b) $ω_0=5$[rad/s]を代入すると、
$|G(jω)|=\left|\displaystyle\frac{10}{j5(1+j)}\right|=\displaystyle\frac{10}{5}×\left|\displaystyle\frac{1}{j(1+j)}\right|$
$j(1+j)=j-1$ なので、大きさは
$\sqrt{1^2+1^2}=\sqrt{2}$
ですので、
$|G(jω)|=2×\displaystyle\frac{1}{\sqrt{2}}=\sqrt{2}=1.41$
答え (2)
2005年(平成17年)問13
ある一次遅れ要素のゲインが $20log_{10}\displaystyle\frac{1}{\sqrt{1+(ωT)^2}}=-10log_{10}(1+ω^2T^2)$[dB]で与えられるとき、その特性をボード線図で表す場合を考える。
角周波数 $ω$[rad/s]が時定数 $T$[s]の逆数と等しいとき、これを( ア )角周波数という。
ゲイン特性は $ω≪\displaystyle\frac{1}{T}$ の範囲では $0$[dB]、$ω≫\displaystyle\frac{1}{T}$ の範囲では角周波数が $10$倍になるごとに( イ )[dB]減少する直線となる。また、 $ω=\displaystyle\frac{1}{T}$ におけるゲインは約 $-3$[dB]であり、その点における位相は( ウ )[◦]の遅れである。
上記の記述中の空自箇所(ア),(イ)及び(ウ)に記入する語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 折れ点 | 10 | 45 |
| (2) | 固有 | 10 | 90 |
| (3) | 折れ点 | 20 | 45 |
| (4) | 固有 | 10 | 45 |
| (5) | 折れ点 | 20 | 90 |
2005年(平成17年)問13 過去問解説
題意は一次遅れ要素のボード線図の問題です。時定数の逆数を折れ線周波数といいます。低周波のゲインは 0[db]で、周波数が高くなるほどゲインは低くなります。例えば周波数が10倍になれば、20db減少し、その位相は45°遅れます。
答え (3)
2006年(平成18年)問13
図1に示す $R-L$ 回路において、端子a,a’間に単位階段状のステップ電圧 $v(t)$[V]を加えたとき、抵抗 $R$[Ω]に流れる電流を $i(t)$[A]とすると、$i(t)$ は図2のようになった。この回路の $R$[Ω],$L$[H]の値及び入力をa,a’間の電圧として、出力を $R$[Ω]に流れる電流としたときの周波数伝達関数 $G(jω)$ の式として、正しいものを組み合わせたのは次のうちどれか。
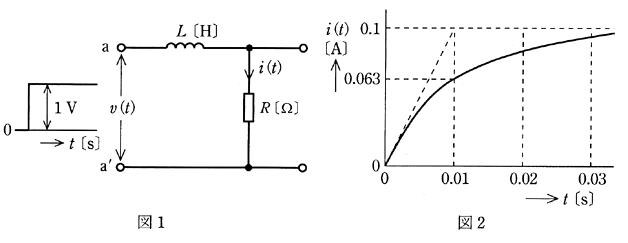
| R[Ω] | L[H] | G(jω) | |
| (1) | 10 | 0.1 | $\displaystyle\frac{0.1}{1+j0.01ω}$ |
| (2) | 10 | 1 | $\displaystyle\frac{0.1}{1+j0.1ω}$ |
| (3) | 100 | 0.01 | $\displaystyle\frac{1}{10+j0.01ω}$ |
| (4) | 10 | 0.1 | $\displaystyle\frac{1}{10+j0.01ω}$ |
| (5) | 100 | 0.01 | $\displaystyle\frac{1}{100+j0.01ω}$ |
2006年(平成18年)問13 過去問解説
図2より、一次遅れ要素の最終値を $K$ とすると、抵抗 $R$ の両端の電圧 $v_2(t)$ は、図2より最終的に電流は 0.1[A]になりますので、
$K=\displaystyle\frac{i(t)_∞}{v(t)_∞}=\displaystyle\frac{0.1}{1}=0.1$
時定数 $T=\displaystyle\frac{L}{R}$ は 0.01 ですので、一次遅れ要素のステップ応答を満たす周波数伝達関数 $G(jω)$ は、
$G(jω)=\displaystyle\frac{0.1}{1+j0.01ω}$
選択肢の中でこの式を満たすのは、$R=10$[Ω],$L=0.1$[H]のみです。
過渡現象の回路では、定常値の約 63 [%] の変化になる時間を時定数 $T$ といい、応答の速さを示す尺度となります。
$RL$ 直列回路の時定数は、 $T=\displaystyle\frac{L}{R}$ となり、$RC$ 直列回路の定数 $T=RC$ となります。
一次遅れ要素の単位ステップ応答を加えた時の伝達関数 $G(s)$ は、$K$ を最終値とすると、
$G(s)=\displaystyle\frac{K}{1+T}$
で与えられます。
答え (1)
2007年(平成19年)問17
図1及び図2について、次の(a)及び(b)に答えよ。
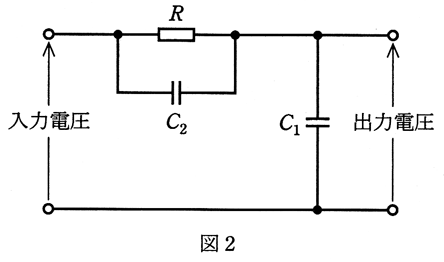
(a) 図1は、抵抗 $R$[Ω]と静電容量 $C_1$[F]による一次遅れ要素の回路を示す。この回路の入力電圧に対する出力電圧の周波数伝達関数を、$G(jω)=\displaystyle\frac{1}{1+jωT_1}$ として表したとき、$T_1$[s]を示す式として,正しいのは次のうちどれか。
ただし、入力電圧の角周波数は $ω$[rad/s]である。
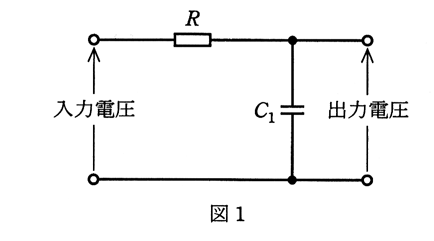
(1) $T_1=\displaystyle\frac{1}{C_1R}$ (2) $T_1=C_1R$ (3) $T_1=1+C_1R$ (4) $T_1=\displaystyle\frac{1+C_1R}{C_1R}$ (5) $T_1=\displaystyle\frac{C_1}{1+C_1R}$
(b) 図2は、図1の回路の過渡応答を改善するために静電容量 $C_2$[F]を付加した回路を示す。この回路の周波数伝達関数を、$G(jω)=\displaystyle\frac{1+jωT_3}{1+jωT_2}$ で表したとき、$T_2$[s]及び $T_3$[s]を示す式として、正しいものを組み合わせたのは次のうちどれか。

2007年(平成19年)問17 過去問解説
(a) 回路に流れる電流を $I(jω)$ とすると、入力電圧 $X(jω)$,出力電圧 $Y(jω)$ は、
$X(jω)=\left(R+\displaystyle\frac{1}{jωC_1}\right)・I(jω)$
$Y(jω)=\displaystyle\frac{1}{jωC_1}・I(jω)$
周波数伝達関数 $G(jω)$ は、
$G(jω)=\displaystyle\frac{Y(jω)}{X(jω)}=\displaystyle\frac{\displaystyle\frac{1}{jωC_1}・I(jω)}{\left(R+\displaystyle\frac{1}{jωC_1}\right)・I(jω)}=\displaystyle\frac{1}{1+jωC_1R}$
周波数伝達関数を、$G(jω)=\displaystyle\frac{1}{1+jωT_1}$ として表したときの、$T_1$[s]は、
$T_1=C_1R$
答え (2)
(b) 回路に流れる電流を $I_2(jω)$ とすると、入力電圧 $X_2(jω)$,出力電圧 $Y_2(jω)$ は、
$X_2(jω)=\left(\displaystyle\frac{\displaystyle\frac{R}{jωC_2}}{R+\displaystyle\frac{1}{jωC_2}}+\displaystyle\frac{1}{jωC_1}\right)・I_2(jω)$
$=\left(\displaystyle\frac{R}{1+jωC_2R}+\displaystyle\frac{1}{jωC_1}\right)・I_2(jω)$
$Y_2(jω)=\displaystyle\frac{1}{jωC_1}・I_2(jω)$
周波数伝達関数 $G(jω)$ は、
$G(jω)=\displaystyle\frac{Y_2jω)}{X_2(jω)}=\displaystyle\frac{\displaystyle\frac{1}{jωC_1}・I_2(jω)}{\left(\displaystyle\frac{R}{1+jωC_2R}+\displaystyle\frac{1}{jωC_1}\right)・I_2(jω)}$
$=\displaystyle\frac{\displaystyle\frac{1}{jωC_1}}{\displaystyle\frac{jωC_1R+1+jωC_2R}{jωC_1(1+jωC_2R)}}$
$=\displaystyle\frac{1+jωC_2R}{1+jω(C_1+C_2)R}$
周波数伝達関数を、$G(jω)=\displaystyle\frac{1+jωT_3}{1+jωT_2}$ で表したとき、$T_2$[s]及び $T_3$[s]を示す式は、
$T_2=(C_1+C_2)R$
$T_3=C_2R$
答え (3)
2008年(平成20年)問17
図1は、調節計の演算回路などによく用いられるブロック線図を示す。次の(a)及び(b)に答えよ。
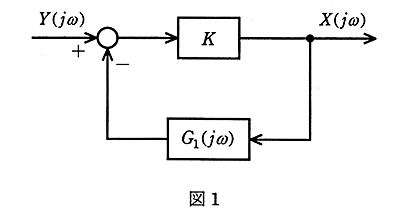
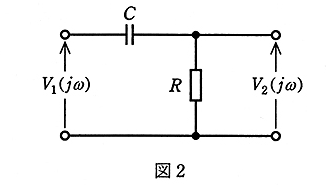
(a) 図2は、図1のブロック $G_1(jω)$ の詳細を示し、静電容量 $C$[F]と抵抗 $R$[Ω]からなる回路を示す。この回路の入力量 $V_1(jω)$ に対する出力量 $V_2(jω)$ の周波数伝達関数 $G_1(jω)=\displaystyle\frac{V_2(jω)}{V_1(jω)}$ を表す式として、正しいのは次のうちどれか。
(1) $\displaystyle\frac{1}{CR+jω}$ (2) $\displaystyle\frac{1}{1+jωCR}$ (3) $\displaystyle\frac{CR}{CR+jω}$ (4) $\displaystyle\frac{CR}{1+jωCR}$ (5) $\displaystyle\frac{jωCR}{1+jωCR}$
(b) 図1のブロック線図において、閉ループ周波数伝達関数 $G(jω)=\displaystyle\frac{X(jω)}{Y(jω)}$ で、ゲイン $K$ が非常に大きな場合の近似式として、正しいのは次のうちどれか。
なお、この近似式が成立する場合、この演算回路は比例プラス積分要素と呼ばれる。
(1) 1+jωCR (2) $1+\displaystyle\frac{CR}{jω}$ (3) $1+\displaystyle\frac{1}{jωCR}$ (4) $\displaystyle\frac{1}{1+jωCR}$ (5) $\displaystyle\frac{1+CR}{jωCR}$
2008年(平成20年)問17 過去問解説
(a) 回路に流れる電流を $I(jω)$ とすると、入力電圧 $V_1(jω)$,出力電圧 $V_2(jω)$ は、
$V_1(jω)=\left(R+\displaystyle\frac{1}{jωC}\right)・I(jω)$
$V_2(jω)=R・I(jω)$
周波数伝達関数 $G_1(jω)$ は、
$G_1(jω)=\displaystyle\frac{V_2(jω)}{V_1(jω)}=\displaystyle\frac{R・I(jω)}{\left(R+\displaystyle\frac{1}{jωC}\right)・I(jω)}=\displaystyle\frac{jωCR}{1+jωCR}$
答え (5)
(b) 図1の閉ループ周波数伝達関数 $G(jω)$ を求めます。
$X=(Y-G_1X)K=KY-KG_1X$
$X(1+KG_1)=KY$
$\displaystyle\frac{X}{Y}=\displaystyle\frac{K}{1+KG_1}=\displaystyle\frac{1}{\displaystyle\frac{1}{K}+G_1}=G$
$K$ が非常に大きい場合、$\displaystyle\frac{1}{K}=0$ になりますので、
$G(jω)=\displaystyle\frac{1}{G_1(jω)}$
(a)で求めた $G_1(jω)$ を代入すると、
$G(jω)=\displaystyle\frac{1}{G_1(jω)}=\displaystyle\frac{1}{\displaystyle\frac{jωCR}{1+jωCR}}$
$=\displaystyle\frac{1+jωCR}{jωCR}=1+\displaystyle\frac{1}{jωCR}$
答え (3)
2010年(平成22年)問13
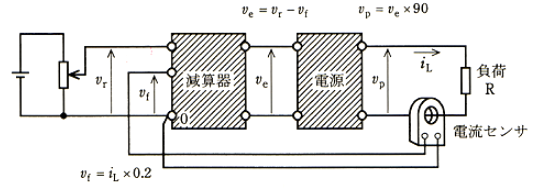
図は、負荷に流れる電流 $i_L$[A]を電流センサで検出して制御するフィードバック制御系である。
減算器では、目標値を設定する電圧 $v_r$[V]から電流センサの出力電圧 $v_f$[V]を減算して、誤差電圧 $v_e=v_r-v_f$ を出力する。
電源は、減算器から入力される入力電圧(誤差電圧)$v_e$[V]に比例して出力電圧 $v_p$[V]が変化し、入力信号 $v_e$[V]が 1[V]のときには出力電圧 $v_p$[V]が 90[V]となる。
負荷は、抵抗 $R$ の値が 2〔Ω〕の抵抗器である。
電流センサは、検出電流(負荷に流れる電流)$i_L$[A]が 50[A]のときに出力電圧 $v_f$[V]が 10[V]となる。
この制御系において目標値設定電圧 $v_r$[V]を 8[V]としたときに負荷に流れる電流 $i_L$[A]の値として、最も近いのは次のうちどれか。
(1) 8.00 (2) 36.0 (3) 37.9 (4) 40.0 (5) 72.0
2010年(平成22年)問13 過去問解説
計算条件を式にしていきます。
$i_L=\displaystyle\frac{v_p}{R}$
$v_p=90v_e$
$v_e=v_r-v_f$
$v_f=0.2i_L$
$v_r$[V]を 8[V]としたときに負荷に流れる電流 $i_L$[A]は、
$i_L=\displaystyle\frac{v_p}{R}=\displaystyle\frac{90v_e}{R}$
$=\displaystyle\frac{(v_r-v_f)×90}{R}$
$=\displaystyle\frac{(8-0.2i_L)×90}{2}$
$=360-9i_L$
$10i_L=360$
$i_L=36.0$
答え (2)
2013年(平成25年)問13
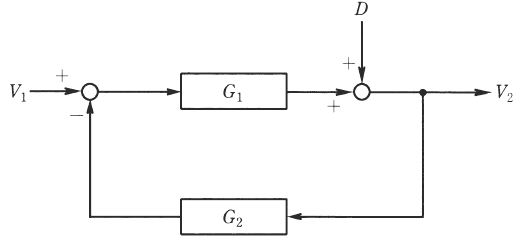
図は、フィードバック制御におけるブロック線図を示している。この線図において、出力 $V_2$ を、入力 $V_1$ 及び外乱 $D$ を使って表現した場合、正しいものを次の(1)~(5)のうちから一つ選べ。
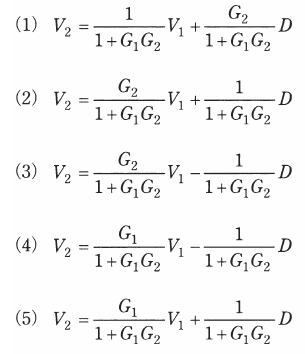
2013年(平成25年)問13 過去問解説
ブロック線図より、
$G_1(V_1-G_2V_2)+D=V_2$
$G_1V_1-G_1G_2V_2+D=V_2$
$V_2(1+G_1G_2)=G_1V_1+D$
$V_2=\displaystyle\frac{G_1}{1+G_1G_2}V_1+\displaystyle\frac{1}{1+G_1G_2}D$
答え (5)
2015年(平成27年)問17
図に示すように、フィードバック接続を含んだブロック線図がある。このブロック線図において、$T=0.2$s、$K=10$としたとき、次の(a)及び(b)の問に答えよ。
ただし、$ω$ は角周波数[rad/s]を表す。
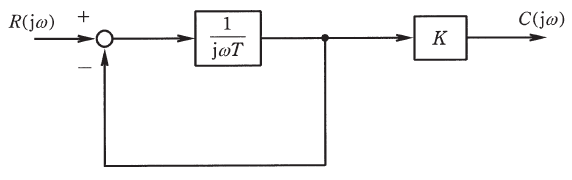
(a) 入力を $R(jω)$、出力を $C(jω)$ とする全体の周波数伝達関数 $W(jω)$ として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) $\displaystyle\frac{10}{1+j0.2ω}$ (2) $\displaystyle\frac{1}{1+j0.2ω}$ (3) $\displaystyle\frac{1}{1+j5ω}$ (4) $\displaystyle\frac{50ω}{1+j5ω}$ (5) $\displaystyle\frac{j2ω}{1+j0.2ω}$
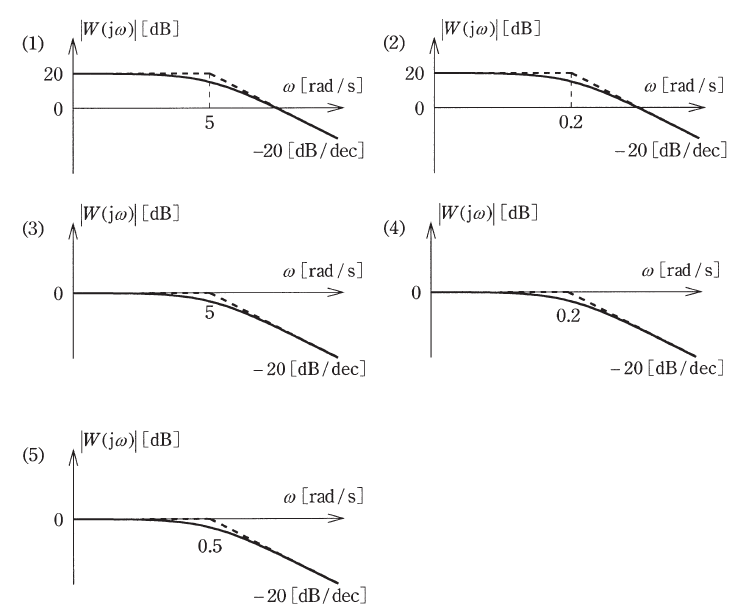
(b) 次のボード線図には、正確なゲイン特性を実線で、その折線近似ゲイン特性を破線で示し、横軸には特に折れ点角周波数の数値を示している。上記(a)の周波数伝達関数 $W(jω)$ のボード線図のゲイン特性として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、横軸は角周波数 $ω$ の対数軸であり、-20[dB/dec]とは、$ω$ が10倍大きくなるに従って $|W(jω)|$ が -20dB 変化する傾きを表している。
2015年(平成27年)問17 過去問解説
(a) 伝達関数 $G=\displaystyle\frac{1}{jωT}$ とすると、ブロック線図より、
$C=(RK-C)G=RGK-CG$
$C(1+G)=RGK$
$\displaystyle\frac{C}{R}=\displaystyle\frac{GK}{1+G}=W$
全体の周波数伝達関数 $W(jω)$ は、
$W(jω)=\displaystyle\frac{C(jω)}{R(jω)}=\displaystyle\frac{GK}{1+G}$
$=\displaystyle\frac{\displaystyle\frac{K}{jωT}}{1+\displaystyle\frac{1}{jωT}}=\displaystyle\frac{K}{1+jωT}=\displaystyle\frac{10}{1+j0.2ω}$
答え (1)
(b) $|W(jω)|$ は、
$|W(jω)|=\displaystyle\frac{10}{\sqrt{1+0.04ω^2}}$
ゲイン特性は $g=20log_{10}|W(jω)|$ で表すことができますので、
$g=20log_{10}|W(jω)|=20log_{10}\displaystyle\frac{10}{\sqrt{1+0.04ω^2}}$
$=20log_{10}10-20log_{10}\sqrt{1+0.04ω^2}$
$=20-10log_{10}(1+0.04ω^2)$
$ω=0$ のとすると、
$g=20-10log_{10}1=20$
ですので、(1)か(2)のグラフに絞られます。
(1)のグラフを判定するために $ω=5$ を代入すると、
$g=20-10log_{10}(1+0.04×5^2)$
$=20-10log_{10}2=17$
グラフと一致します。
(2)のグラフを判定するために $ω=0.2$ を代入すると、
$g=20-10log_{10}(1+0.04×0.2^2)$
$=20-10log_{10}1.0016≒20$
グラフと一致しません。
答え (1)





