第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の電力科目に出題される「電線のたるみと実長」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の電力科目の試験で、実際に出題された「電線のたるみと実長」の過去問題も解説しています。
電線のたるみと実長
電線は、断線しないように「たるみ」を持たせて架線しなければなりません。たるみを大きくすれば、支持物の高さは高くなると共に電線の短絡故障につながりやすくなります。また、逆にたるみを小さくするために電線を強く張れば、支持物の設計強度が大きくなると共に冬季の着氷雪時には過大な張力が加わるおそれがあります。
電線のたるみの大きさを弛度(ちど)といい、次の式で求めることができます。
電線のたるみの大きさを求める式
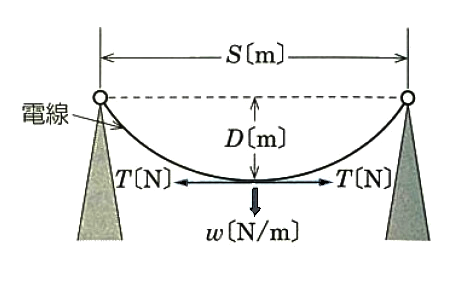
$D=\displaystyle \frac{ wS^2 }{ 8T }$
$D$[m]:たるみ
$w$[N/m]:電線1m当たりの荷重
$S$[m]:径間
$T$[N]:水平張力
電線の実長
電線を支持物間に架線すると、 電線にはたるみが発生するため、電線の実際の長さは、径間よりも長くなります。
たるみを考慮した電線の長さ(実長)を求める公式は次のようになります。
電線の長さ(実長)を求める公式
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$
$L$[m]:電線の実長
$S$[m]:径間
$D$[m]:たるみ
電線の線膨張
銅やアルミなどの金属は、温度が上昇すると、膨張により電線は長くなります。温度が下がると収縮する性質を持っているため、これらの金属を使用する電線は、温度によって膨張、収縮してその長さは変化します。
電線の膨張する割合を表すものとして「線膨張係数」があり、これにより 温度上昇時の膨張した電線の長さを求めることができます。温度上昇後の電線の長さを L2[m]とすると、次の式で求めることができます。
電線の線膨張による電線長さを求める式
$L_2=L_1{1+α(T_2-T_1)}$
L1[m]:温度上昇前の長さ
α:電線の線膨張係数
T1[℃]:温度上昇前の温度
T2[℃]:温度上昇後の温度
電線の荷重
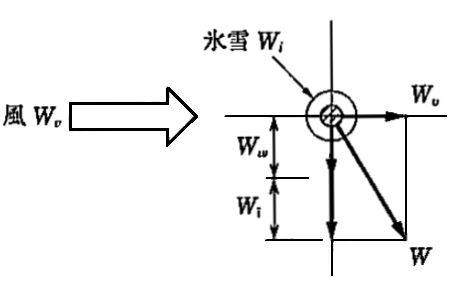
電線を架線するには、電線自体の荷重 Ww と風圧荷重 Wv 、また被氷雪による荷重 Wi に十分耐えれるように安全率を見込んでおかなければなりません。合成荷重を W とした場合、各荷重の関係は、次の式で表すことができます。
電線の荷重を求める式
$W=\sqrt{{W_v}^2+(W_w+W_i)^2}$
Ww:電線質量による荷重[N/m]
Wv:風圧荷重[N/m]
Wi:被氷雪質量による荷重[N/m]
支線
配電線路の端末で電線張力が平衡して支持物に加わっていない箇所に、不平衡張力に耐えるために支線を設置します。材料は、亜鉛めっき鋼より線(2.6~4〔mm〕)を用いています。尚、鉄塔には支線を取り付けません。
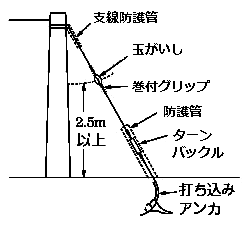
- 支線防護管:配電線作業時の感電防止
- 玉がいし:漏電による感電防止
- ターンバックル:支線の緩み取り
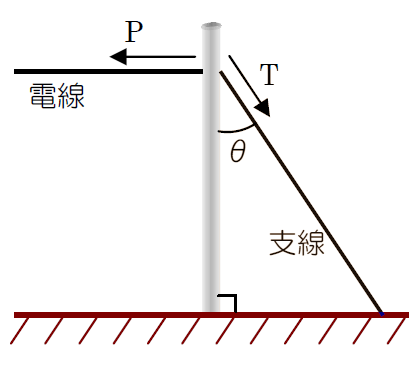
電柱は電線の張力に、支線と支柱で強度を維持しています。電線張力を P[kg]とするとき、支線で支える力 T[kg]は、次の式で求めることができます。
電線の水平張力と支線の関係を表す式
$T=\displaystyle \frac{ P }{ sinθ }$
$P$[kg]:電線の水平張力
$T$[kg]:支線の張力
$θ$:電柱と支線のなす角度
電験三種-電力の過去問解説:電線のたるみと実長
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の電力科目で出題された問題です。
1998年(平成10年)問6
図のような高低差のない支持点A、Bで、径間長S架空送電線において、架空の水平張力 T を調整してたるみ D を 10[%]小さくし、電線地上高を高くしたい。この場合の水平張力の値として、 正しいのは次のうちどれか。ただし、両側の鉄塔は十分な強度があるものとする。
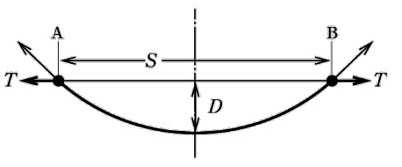
(1) 0.92T (2) 0.9T (3) $\displaystyle\frac{T}{\sqrt{0.9}}$ (4) $\displaystyle\frac{T}{0.9}$ (5) $\displaystyle\frac{T}{0.9^2}$
1998年(平成10年)問6 過去問解説
調整前の水平張力を T を たるみを D 、調整後の水平張力を T’ を たるみを D’ とすると、
D’=0.9D
調整前の水平張力を T’ は
$D’=\displaystyle \frac{ wS^2 }{ 8T’ }$
$T’=\displaystyle \frac{ wS^2 }{ 8D’ }=\displaystyle \frac{ wS^2 }{ 8D }×\frac{ 1 }{ 0.9 }=T×\displaystyle\frac{ 1 }{ 0.9 }$
答え (4)
1998年(平成10年)問7
送電線に加わる荷重と電線質量による荷重との比(負荷係数)は、被氷雪を考慮した場合、正しいのは次のうちどれか。ただし、Ww、Wv 及び Wi は、次の荷重を表すものとする。
Ww : 電線質量による荷重[N/m]、Wv : 風圧荷重[N/m]、Wi : 被氷雪質量による荷重[N/m]
(1) $\displaystyle\frac{{W_v}^2+{W_w}^2+{W_i}^2}{{W_w}^2}$ (2) $\displaystyle\frac{\sqrt{{W_v}+{W_w}+{W_i}}}{W_w}$ (3) $\displaystyle\frac{\sqrt{{W_v}^2+{W_w}^2+{W_i}^2}}{W_w}$ (4) $\displaystyle\frac{\sqrt{({W_v}+{W_w})^2+{W_i}^2}}{W_w}$ (5) $\displaystyle\frac{\sqrt{{W_v}^2+({W_w}+{W_i})^2}}{W_w}$
1998年(平成10年)問7 過去問解説
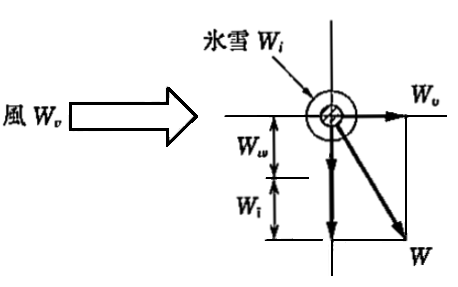
$W=\sqrt{{W_v}^2+(W_w+W_i)^2}$
Ww:電線質量による荷重[N/m]
Wv:風圧荷重[N/m]
Wi:被氷雪質量による荷重[N/m]
題意より、負荷係数は $\displaystyle \frac{ W }{ Ww }$
答え (5)
2003年(平成15年)問16
架空電線路の径間、電線の長さ及びたるみに関して、次の(a)及び(b)に答えよ。
(a) 径間を S[m]、電線のたるみを D[m]とするとき、電線の長さ L[m]を示す式として、正しいのは次のうちどれか。
(1) $S+\displaystyle \frac{ 8D^2 }{ 3S }$ (2) $S+\displaystyle \frac{ 8D }{ 3S }$ (3) $S+\displaystyle \frac{ 3D^2 }{ 8S }$ (4) $S+\displaystyle \frac{ 3D }{ 8S }$ (5) $S+\displaystyle \frac{ D^2 }{ 3S }$
(b) 架空電線路の径間が 50[m]で、導体の温度が 40[℃]のときのたるみは 1[m]であった。この電線路の導体の温度が 70[℃]になったときのたるみ[m]の値として、最も近いのは次のうちどれか。
ただし、電線の膨張係数は 1[℃]につき 0.000017 とし、張力による電線の伸縮は無視するものとする。
(1) 1.03 (2) 1.14 (3) 1.22 (4) 1.34 (5) 1.47
2003年(平成15年)問16 過去問解説
(a) 電線の実長の公式より
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$
答え (1)
(b) 40℃のときの電線の実長を L40 とすると
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$
$\begin{eqnarray}L_{40}&=&50+\displaystyle \frac{ 8×1^2 }{ 3×50 }\\\\&=&50.0533[m]\end{eqnarray}$
70℃のときの電線の実長を L70 とすると
$L_2=L_1{1+α(T_2-T_1)}$
$\begin{eqnarray}L_{70}&=&50.0533{1+0.000017 (70-40)}\\\\&=&50.07883[m]\end{eqnarray}$
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$ より
$50.07883=50+\displaystyle \frac{ 8D^2 }{ 3×50 }$
$D≒1.22$
答え (3)
2006年(平成18年)問14
両端の高さが同じで径間距離 250[m]の架空電線路があり、電線 1[m]当たりの重量は 20.0[N]で、風圧荷重は無いものとする。
いま、水平引張荷重が 40.0[kN]の状態で架線されているとき、たるみ D[m]の値として、最も近いのは次のうちどれか。
(1) 2.1 (2) 3.9 (3) 6.3 (4) 8.5 (5) 10.4
2006年(平成18年)問14 過去問解説
$D=\displaystyle \frac{ wS^2 }{ 8T }=\displaystyle \frac{ 20×250^2 }{ 8×40×10^2 }=3.9$[m]
答え (2)
2012年(平成24年)問13
図のように高低差のない支持点 A,,B で支持されている径間 S が 100[m]の架空電線路において、導体の温度が 30[℃]のとき、たるみ D は 2[m] であった。
導体の温度が 60[℃]になったとき、たるみ D[m]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、電線の線膨張係数は 1[℃]につき 1.5×10-5 とし、張力による電線の伸びは無視するものとする。
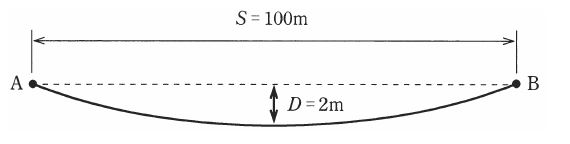
(1) 2.05 (2) 2.14 (3) 2.39 (4) 2.66 (5) 2.89
2012年(平成24年)問13 過去問解説
30℃のときの電線の実長を $L_{30}$ とすると
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$
$\begin{eqnarray}L_{30}&=&100+\displaystyle \frac{ 8×2^2 }{ 3×100 }\\\\&=&100.10667[m]\end{eqnarray}$
60℃のときの電線の実長を $L_{70}$ とすると
$L_2=L_1{1+α(T_2-T_1)}$
$\begin{eqnarray}L_{60}&=&100.10667{1+1.5×10^{-5}× (60-40)}\\\\&=&100.1517[m]\end{eqnarray}$
$L=S+\displaystyle \frac{ 8D^2 }{ 3S }$ より
$100.1517=100+\displaystyle \frac{ 8D^2 }{ 3×100 }$
$D≒2.385$
答え (3)
2013年(平成25年)問9
図のように、架線の水平張力 T[N]を支線と追支線で、支持物と支線柱を介して受けている。支持物の固定点Cの高さを h1[m]、支線柱の固定点Dの高さを h2[m]とする。また、支持物と支線柱の距離 AB をℓ1[m]、支線柱と追支線地上固定点Eとの根開き BEを ℓ2[m]とする。
支持物及び支線柱が受ける水平方向の力は、それぞれ平衡しているという条件で、追支線にかかる張力 T2[N]を表した式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、支線、追支線の自重及び掲示していない条件は無視する。
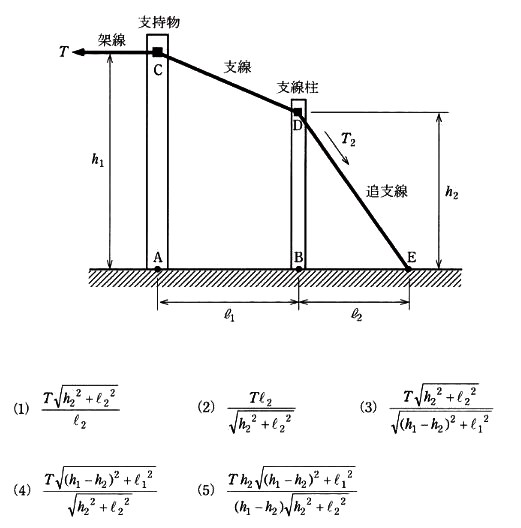
2013年(平成25年)問9 過去問解説
力の関係は次の図のとおりになります。
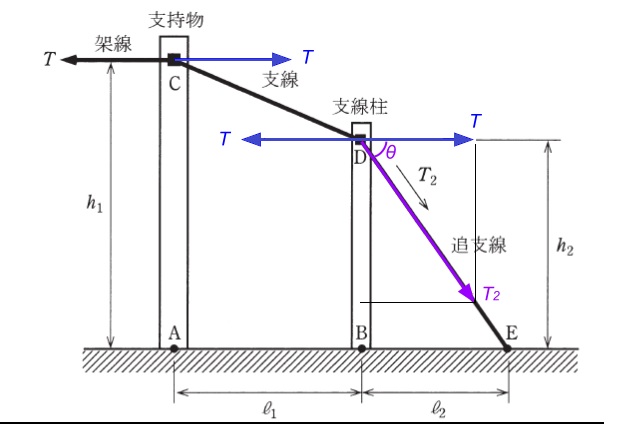
水平張力 $T$ と追支線にかかる張力 T2 の関係は、
$cosθ=\displaystyle \frac{ T }{ T_2 }=\displaystyle \frac{ l_2 }{ \sqrt{ h_2^2+l_2^2 } }$
$T_2=\displaystyle \frac{ T\sqrt{ h_2^2+l_2^2 } }{ l_2 }$
答え (1)
2017年(平成29年)問8
支持点間が 180 m、たるみが 3.0 mの架空電線路がある。いま架空電線路の支持点間を 200 mにしたとき、たるみを 4.0 mにしたい。電線の最低点における水平張力をもとの何[%]にすればよいか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、支持点間の高低差はなく、電線の単位長当たりの荷重は変わらないものとし、その他の条件は無視するものとする。
(1) 83.3 (2) 92.6 (3) 108.0 (4) 120.0 (5) 148.1
2017年(平成29年)問8 過去問解説
支持点間が 180 m、たるみが 3.0 m の架空電線路の水平張力 T は
$3=\displaystyle \frac{ w×180^2 }{ 8T }$
$T=\displaystyle \frac{ w×180^2 }{ 3×8 }$
支持点間が 200 m、たるみが 4.0 m の架空電線路の水平張力 $T’$ は
$4=\displaystyle \frac{ w×200^2 }{ 8T’ }$
$T’=\displaystyle \frac{ w×200^2 }{ 4×8 }$
T と T’ の比は
$\displaystyle \frac{ T’}{ T }=\displaystyle \frac{ \displaystyle\frac{ w×200^2 }{ 4×8 } }{ \displaystyle \frac{ w×180^2 }{ 3×8 } }=0.9259$
答え (2)
電験三種の電力科目に出題される「送電線路」のページ






