第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、電気に関する基礎理論「三相交流回路」について、解説しています。
三相交流とは?
工場やビルなどの大電力を必要とする建物では、3本の電線を用いて送られてくる三相交流が用いられています。三相交流は、位相を120°ずつずらした3系統の単相交流を組み合わせたものです。
磁界の中でコイルを回転させると、正弦波交流が発生します。このときコイルを 120°ずつずらして回転させると、同じ周波数で3つの正弦波交流が発生します。
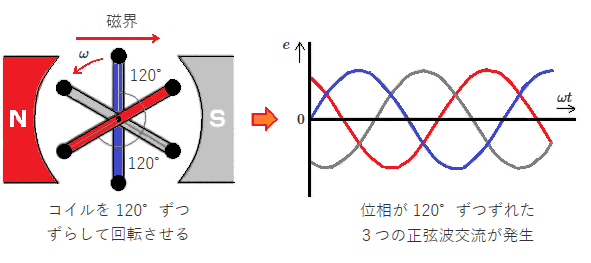
三相交流の波形は、どの瞬間をとっても3つの交流の振幅の和はゼロになります。
三相交流の電圧と電流
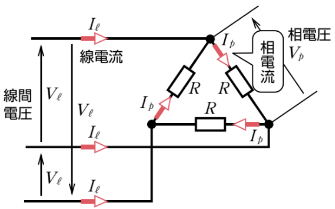
三相交流の結線にはY(スター)結線とΔ(デルタ)結線があります。
三相交流を送る3本の電線の間の電圧を線間電圧、1相当たりの負荷にかかる電圧を相電圧といいます。また、3本の線を流れる電流を線電流、1相当たりの負荷に流れる電流を相電流といいます。
Y(スター)結線
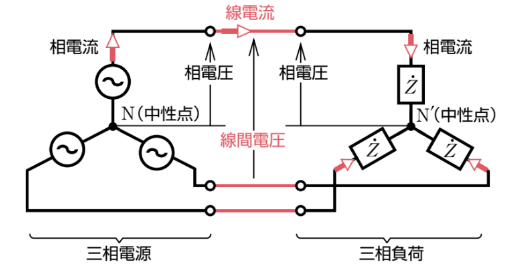
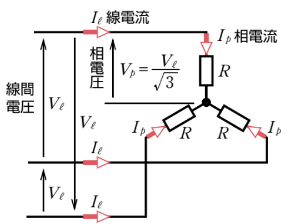
Y(スター)結線の電圧と電流の関係
$V_l=\sqrt{3}V_p$
$I_l=I_p$
$V_l$:線間電圧
$V_p$:相電圧
$I_l$:線電流
$I_p$:相電流
Δ(デルタ)結線
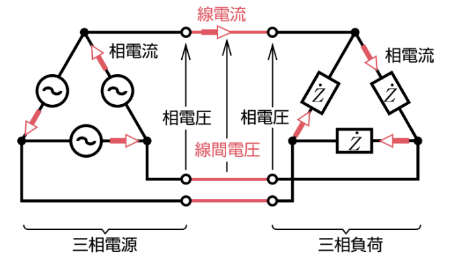
Δ(デルタ)結線の電圧と電流の関係
$V_l=V_p$
$I_l=\sqrt{3}I_p$
$V_l$:線間電圧
$V_p$:相電圧
$I_l$:線電流
$I_p$:相電流
三相交流の電力と力率
三相交流回路では、電力 $P$[W]を、次の式で表すことができます。
Y(スター)結線

$P=3V_pI_pcosθ$[W]
$=3\displaystyle\frac{V_l}{\sqrt{3}}I_lcosθ$[W]
$=\sqrt{3}V_lI_lcosθ$[W]
Δ(デルタ)結線

$P=3V_pI_pcosθ$[W]
$=3V_l\displaystyle\frac{I_l}{\sqrt{3}}cosθ$[W]
$=\sqrt{3}V_lI_lcosθ$[W]
尚、$cosθ$ は力率とで、単相電力と同じように、皮相電力 $S$[VA]、有効電力 $P$[W]、無効電力 $Q$[var]で表すことができます。
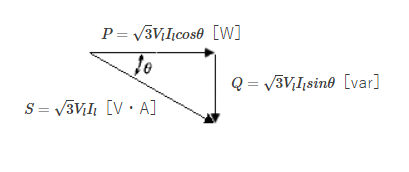
皮相電力:$S=\sqrt{3}V_lI_l$[VA]
有効電力:$P=\sqrt{3}V_lI_lcosθ$[W]
無効電力:$Q=\sqrt{3}V_lI_lsinθ$[var]
上記3式の関係は次のように表すことができます。
$S=\sqrt{P^2+Q^2}$
電気に関する基礎理論:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 三相交流回路①
図のように三相負荷に三相交流電圧を加えたとき、各線に 20[A]の電流が流れた。線間電圧[V]は。
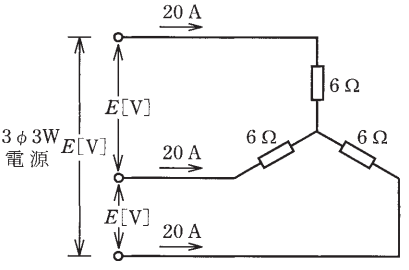
イ. 120 ロ. 173 ハ. 208 二. 240
Y(スター)結線は、線電流 $I_l$ と相電流 $ I_p$ は等しいので、
$I_l=I_p=20$[A]
相電圧 $V_p$[V]は、オームの法則より、
$V_p=RI_p=6×20=120$[V]
線間電圧 $V_l$[V]は、
$V_l=\sqrt{3}V_p=1.73×120≒208$[V]
答え(ハ)
2008年(平成20年)問5
2014年(平成26年)下期 問4
2016年(平成28年)下期 問5
2018年(平成30年)上期 問5
問2 三相交流回路②
図のように三相負荷に三相交流電圧を加えたとき、各線に 15[A]の電流が流れた。線間電圧 $E$[V]は。
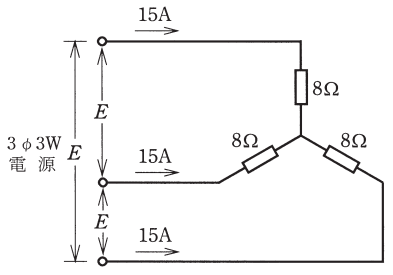
イ. 120 ロ. 169 ハ. 208 二. 240
Y(スター)結線は、線電流 $I_l$ と相電流 $ I_p$ は等しいので、
$I_l=I_p=15$[A]
相電圧 $V_p$[V]は、オームの法則より、
$V_p=RI_p=8×15=120$[V]
線間電圧 $E$[V]は、
$E=\sqrt{3}V_p=1.73×120≒208$[V]
答え(ハ)
2011年(平成23年)下期 問5
問3 三相交流回路③
図のような三相3線式回路に流れる電流 $I$[A]は。
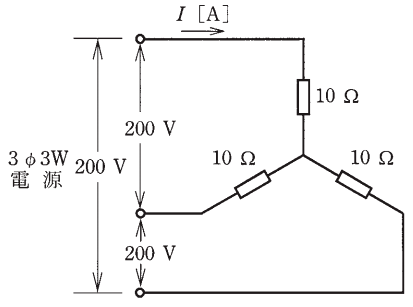
イ. 8.3 ロ. 11.6 ハ. 14.3 二. 20.0
相電圧を $V_p$[V]、線間電圧を $V_l$[V]とすると、
$V_p=\displaystyle\frac{V_l}{\sqrt{3}}=\displaystyle\frac{200}{1.73}≒115.6$[V]
線電流 $I_l$[A]は、オームの法則より、
$I_l=\displaystyle\frac{V_p}{R}=\displaystyle\frac{115.6}{10}≒11.6$[A]
答え(ロ)
2012年(平成24年)下期 問5 類似
2015年(平成27年)下期 問5
2019年(令和元年)下期 問5 類似
問4 三相交流回路④
図のような三相3線式回路に流れる電流 $I$[A]は。
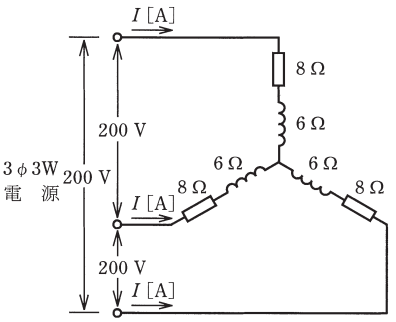
イ. 8.3 ロ. 11.6 ハ. 14.3 二. 20.0
相電圧を $V_p$[V]、線間電圧を $V_l$[V]とすると、
$V_p=\displaystyle\frac{V_l}{\sqrt{3}}=\displaystyle\frac{200}{1.73}≒115.6$[V]
線電流 $I_l$[A]は、オームの法則より、
$I_l=\displaystyle\frac{V_p}{Z}=\displaystyle\frac{115.6}{\sqrt{6^2+8^2}}≒11.6$[A]
答え(ロ)
2018年(平成30年)下期 問5
問5 三相交流回路⑤
図のような三相3線式回路の全消費電力[kW]は。
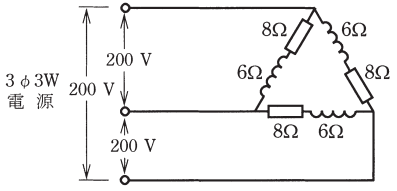
イ. 2.4 ロ. 3.2 ハ. 7.2 二. 9.6
一相分のインピーダンスを $Z$[Ω]、力率を $cosθ$ とすると、
$Z=\sqrt{R^2+{X_L}^2}=\sqrt{8^2+6^2}=10$[Ω]
$cosθ=\displaystyle\frac{R}{Z}=\displaystyle\frac{8}{10}=0.8$
相電流を $I_p$[A]、線電流を $I_l$[A]とすると、オームの法則より、
$I_p=\displaystyle\frac{V_p}{Z}=\displaystyle\frac{200}{20}=0.8$[A]
$I_l=\sqrt{3}I_p=20\sqrt{3}$[A]
全消費電力 $P$ は、
$P=\sqrt{3}V_lI_lcosθ=\sqrt{3}×200×20\sqrt{3}×0.8=9.6$[kW]
答え(二)
2006年(平成18年)問5
2010年(平成22年)問5
2013年(平成25年)下期 問5
2014年(平成26年)上期 問5
2017年(平成29年)下期 問5 類題
2019年(令和元年)上期 問5
問6 三相誘導電動機の力率
定格電圧 V[V]、定格電流 I[A]の三相誘導電動機を定格状態で時間 t[h]の間、連続運転したところ、消費電力量が W[kW·h]であった。
この電動機の力率[%]を表す式は。
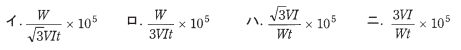
消費電力量を表す式は、次式のとおりです。
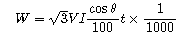
答え(イ)
2011年(平成24年)上期 問5
2016年(平成28年)上期 問5



