第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の電力科目に出題される「パスカルの原理とベルヌーイの定理」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の電力科目の試験で、実際に出題された「パスカルの原理とベルヌーイの定理」の過去問題も解説しています。
密度と比重
密度とは ?
物質の密度とは、単位体積あたりの質量のことです。 物質の密度 ρ(読み:ロー) は、質量 M を単位体積 V で割った値となり、次の式で求めることができます。
$ρ=\displaystyle\frac{ M}{ V} $
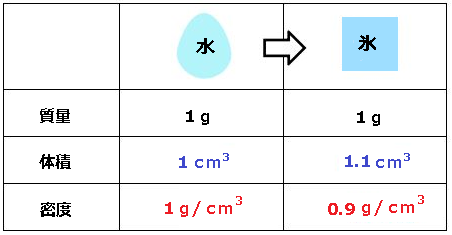
密度の単位には、kg/m3 や g/cm3 などが使われます。密度は物質の状態によって変化します。 例えば、水が氷に変化すると、体積が大きくなりますが、密度は小さくなります。
水の入ったコップに氷を入れると、水に浮かびます。これは氷の方が密度が小さいからです。つまり、密度は状態量を示しており、物質の種類や温度,圧力などによって変化します。
比重とは?
比重とは、ある物質の密度と、4℃の水の密度との比のことです。 例えば、鉄の密度は、7874[kg/m3]です。4℃の水の密度は、1000[kg/m3]です。したがって、たとえば鉄の比重は次の式で求めることができます。
$鉄の比重=\displaystyle \frac{ 鉄の密度 }{ 水の密度 }=\displaystyle \frac{ 7874 }{ 1000 }=7.874$
比重が1より大きい場合は水に沈み、1より小さい場合は水に浮かびます。 比重は、水に対する比であるため、単位が存在しません。
圧力について
圧力とは?
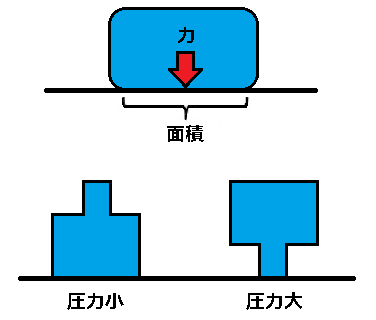
圧力とは、単位面積に対して垂直に働く力のことです。 床の上に置かれた荷物によって働く圧力は、「かかる力」を「受ける面積」で割って求めることができます。
$圧力=\displaystyle \frac{ 力 }{ 面積 }$
例えば、下側の図のように同じ重量を持つ荷物であっても、受ける面積が異なると、圧力も異なります。
圧力の単位
圧力の単位には、Pa(パスカル) が使われます。 以前の圧力の単位は、[kgf/cm2]であったため、感覚的に理解しやすかったのですが、国際単位系である [Pa] が一般的に使われるようになりました。
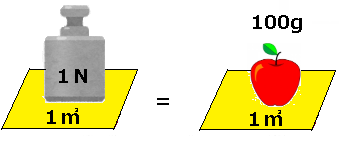
1[Pa]とは、 1平方メートル[m2]の面積あたりに1ニュートン[N]の力が作用したときの圧力です。1[Pa]を工学単位系である、[kgf]に換算すると、9.8[N]= 1[kgf]であるため、 1[Pa] ≒ 0.1[kgf/cm2]となります。
1[Pa]は、1[m2]の床の上に、りんご(約100g)がおかれているくらいの力がかかっていることを示しています。このように表現してみると、1[Pa]とは非常に小さな圧力であることがわかります。
絶対圧とゲージ圧
圧力には、絶対圧とゲージ圧の2種類があります。ゲージ圧は大気圧を基準とした力です。大気圧より高い圧力を正圧、低い圧力を負圧といいます。絶対圧は、絶対真空をゼロとして圧力を表現します。
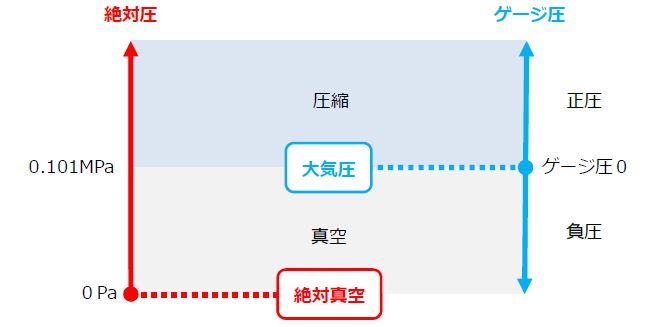
絶対圧とゲージ圧の関係は、「ゲージ圧=絶対圧-大気圧」となります。
私たちは空気の底に住んでおり、普段感じることはありませんが、空気の重さを体で受けています。そして海面上では、1cm2あたり約1kgfの空気の力(0.101MPa)がかかっています。この海面上で空気から受ける力を1気圧(1atm)といいます。なお、大気圧は、山に登ると、自分の上に載っている空気の量が減るため、小さくなります。
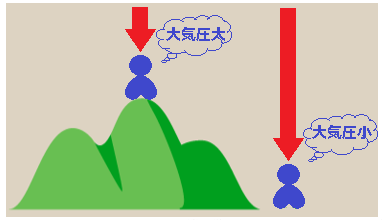
パスカルの原理
静止している流体に加わる圧力はどこでも等しくなります。例えば、自動車のタイヤの空気圧は、どこを測定ポイントとしても同じです。また、その時にかかる圧力は物体に対して常に垂直です。このように静止している流体では、同じ圧力が全てに伝わって等しくなります。これを「パスカルの原理」といいます。
このパスカルの原理の考え方を用いて、小さな力で大きな力を得ることができます。
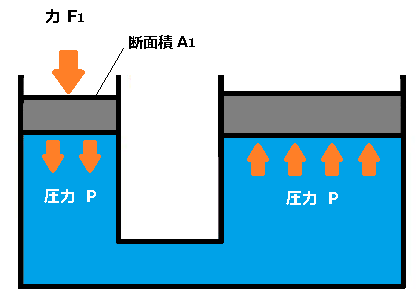
図1のように小さなシリンダーに力 F を加えたとき、発生する圧力 P は、
$P=\displaystyle\frac{F_1}{A_1}$
となります(圧力=力÷面積)。発生した圧力 P は、大きなシリンダーへ伝達されます。
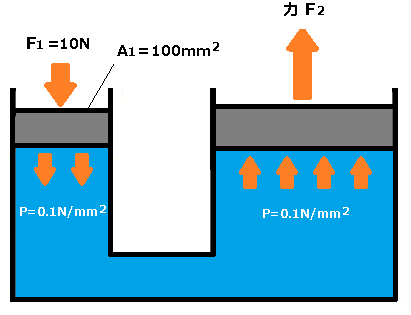
例えば、 F1=10[N],A1= 100[mm2]としたとき、発生する圧力 P[N/mm2]は、
$P=\displaystyle\frac{10}{100}=0.1$[N/mm2]=$0.1$[MPa]
となります(図2)。
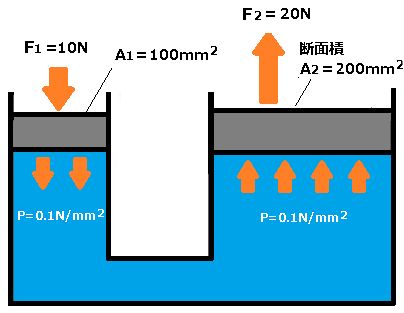
発生した圧力は、大きなシリンダーに同じ圧力で伝わります。このとき、断面積 A2=200[mm2]の大きなシリンダーを持ち上げる力 F2[N]は、次の式で求められます。
$F_2=P×A_2=0.1×200=20$[N]
以上のように、断面積が2倍となり、力は入力値の2倍に増やすことができます(図3)。
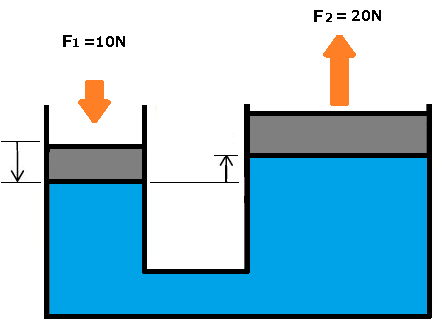
ここで、シリンダー内の流体が非圧縮性流体の場合、発生する力は2倍となります、押し上げる距離は、1/2になります。 つまり、大きな力を得る代わりに、押し込む距離が増えるということになります(図4)。
パスカルの原理のポイント
- 静止している流体に加わる圧力はどこでも等しい
- 同じ面積あたりにかかる力は等しく、受ける力は面積に比例する
- 小さな力で大きな力を生み出すことが可能となる
速度と流量
速度とは?
速度とは単位時間当たりの移動する距離のことです。単位は、m/s や km/h などが使われます。例えば、自動車の速度は時速 60[km/h]のように表現され、単位時間あたりに移動する距離を示します。
ここで、微小時間 dt に移動した距離を dx としたときの速度 V は、
$V=\displaystyle \frac{dx}{dt}$
となります。
流量とは?
流量とは、ある断面を「単位時間当たりに通過する流体の体積」のことです。単位は m3/s や ℓ/minなどが使われます。例えば、水道の蛇口を全開にしたとき、1分間に20ℓ流れる場合の流量は 20[ℓ/min]と表現されます。
流量 $Q$ は、図のように断面積 A を単位時間あたりに通過した流体の体積となります。流体の体積は、「断面積(A)×流体が移動した距離(dx)」です。つまり、流量 Q は、流体の体積を微小時間で割って求めることができます。
$Q=\displaystyle\frac{Adx}{dt}$
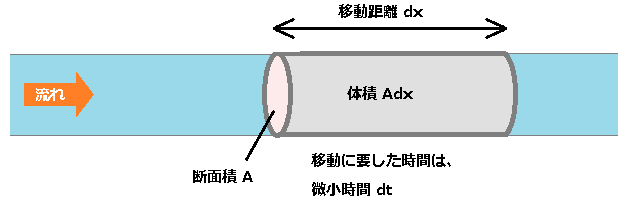
速度 V は $V=\displaystyle \frac{dx}{dt}$ なので、
流量(Q)= 断面積(A)× 速度(V)
となります。
質量保存の法則
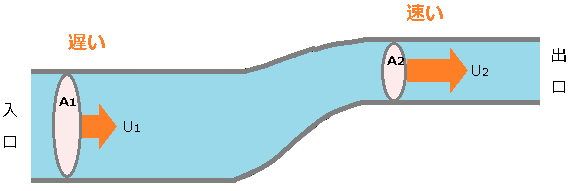
密度変化を無視できない流体の定常流れにおいて、図のような任意の断面(A1やA2)を通過する単位時間あたりに流れる流量(質量流量)は等しくなります。
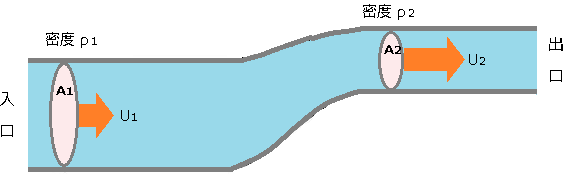
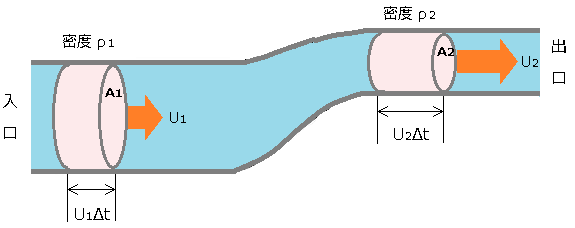
断面 A1 と断面 A2 を単位時間あたりに流れる流量を計算してみます。 単位時間を Δt とすると、流れた距離は、「速度×時間」なので、U×Δt となります。
微小時間 Δt 経過後、断面 A1 と断面 A2 を通過した質量は、「質量=ρ×体積」ですので、
断面 A1 を通過した質量 $=ρ_1×(A_1×U_1ΔT)$
断面 A2 を通過した質量 $=ρ_2×(A_2×U_2ΔT)$
「断面Aを通過した質量=断面 B を通過した質量」ですので、
$ρ_1×(A_1×U_1ΔT)=ρ_2×(A_2×U_2ΔT)$
$ρ_1×A_1×U_1=ρ_2×A_2×U_2$
この関係を「質量保存の法則」といいます。
単位時間あたりに流れる流体の体積(体積流量)が一定ならば、断面積が大きいほど流体の流速は遅く、断面積が小さければ流速が早いということになります。
ベルヌーイの定理
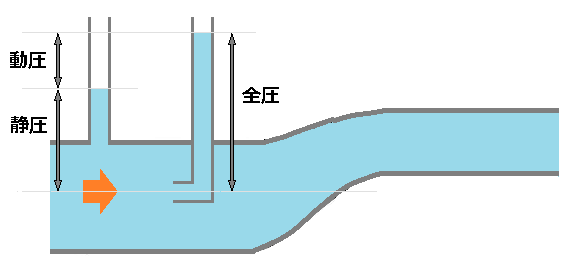
静圧と動圧
圧力には、静圧と動圧があります。 動圧とは、流れによって生じる力です。例えば、人が風を受けるときの力です。このとき、風の速度が速くなればなるほど、力は大きくなります。 厳密には、このとき、受けている力は「動圧+静圧」となります。
動圧は流れ方向に対して、平行に細い管を取り付けることで測定した圧力から静圧を差し引いた値となります。静圧は流れ方向に対して、直角に空けた細い管の先に圧力計を取り付けることで測定することができます。
なお、静圧と動圧を足した圧力を全圧と呼びます。
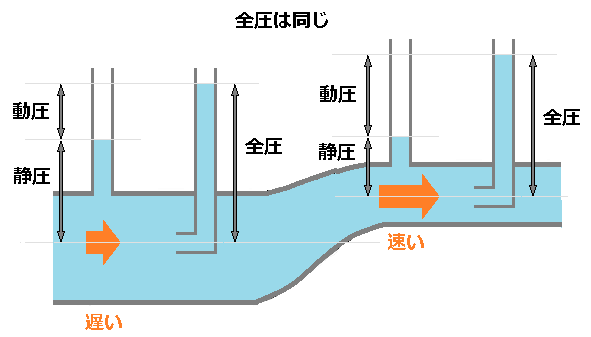
下流の細い管路での動圧と静圧を測定します。 質量保存の法則より、下流の細い管路の流速は太い管路の流速より早くなります。つまり、細い管路の動圧は、太い管路の動圧より大きくなります。
細い管路では、動圧は大きくなりますが、その分静圧は小さくなります。これは、管路の断面積が変化しても全ての位置で全圧は等しくなるからです。
エネルギー保存の法則
エネルギーには、位置エネルギー,運動エネルギー,熱エネルギー,電気エネルギーなど様々な形態があります。
エネルギーとは、仕事をする能力のことであり、これらのエネルギーは、互いに変換することが可能です。そして、変換前後のエネルギーの総和は等しくなります。 これを「エネルギー保存の法則」といいます。
例えば、高さ h の位置から m[kg]のボールを落下させた場合、平面Aの位置では、ボールに重力が加わっているため、重力によって仕事をすることができるエネルギーである「位置エネルギー」が存在します。位置エネルギーを U とすると、
$U=mgh$
となります。
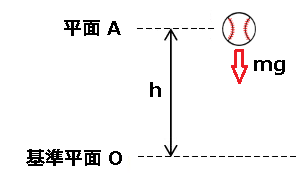
次に、基準平面Oまでボールを自由落下させた際、ボールが速度 v で運動したとしましょう。このとき、最初に持っていた位置エネルギーが運動エネルギーに変換されることになり、運動エネルギー F は、
$F=\displaystyle\frac{ 1 }{ 2 }mv^2$
となります。
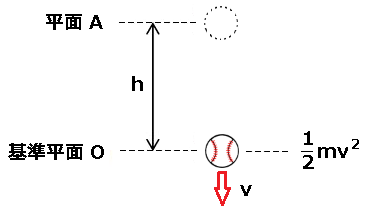
ボールが持っていた位置エネルギーは、落下するにつれて減少し、基準平面に達したときの位置エネルギーは完全にゼロとなり、反対に運動エネルギーは増加します。 これがエネルギー保存の法則です。
| 平面Aにおける エネルギーの総和 | 「運動エネルギー」+「位置エネルギー」$=0+mgh$ |
| 基準平面Oにおける エネルギーの総和 | 「運動エネルギー」+「位置エネルギー」$=\displaystyle \frac{ 1 }{ 2 }mv^2+0$ |
平面Aにおけるエネルギーの総和と基準平面Oにおけるエネルギーの総和は等しくなるため、
$mgh=\displaystyle \frac{ 1 }{ 2 }mv^2$
となります。
ベルヌーイの定理
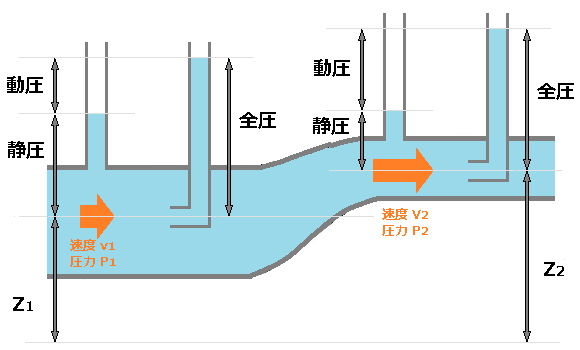
太い管路における流体の速度 v1[m/s]、圧力 P1[Pa]、高さ h1[m]とし、細い管路における流体の速度 v2[m/s]、圧力 P2[Pa]、高さ h2[m]としたとき、エネルギーの総和は、太い管路と細い管路で等しくなります。
管路におけるエネルギーの総和は、「圧力エネルギー+速度エネルギー+位置エネルギー」です。水の密度を $ρ$ とすると、
$P_1+\displaystyle \frac{ 1 }{ 2 }ρv_1^2+ρgh_1=P_2+\displaystyle \frac{ 1 }{ 2 }ρv_2^2+ρgh_2$
上式を密度で割ると、
$\displaystyle \frac{ P_1 }{ ρg }+\displaystyle \frac{ v_1^2 }{ 2g }+h_1=\displaystyle \frac{ P_2 }{ ρg }+\displaystyle \frac{ v_2^2 }{ 2g }+h_2$
水の持つエネルギーを水柱の高さ[m]に置き換えたものを水頭といい、管路の流れを水頭で表すと次の図のようになります。
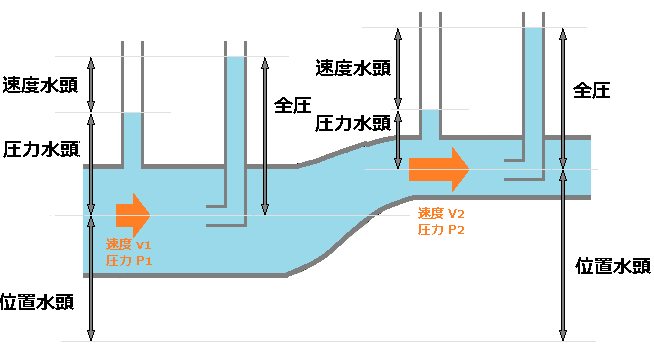
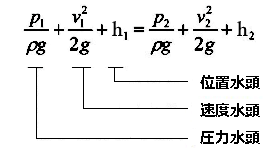
以上がベルヌーイの定理となります。この式が成り立つのは、非粘性・非圧縮性の理想流体です。
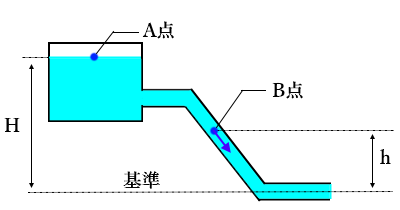
ベルヌーイの定理を水頭を使って表す公式
$\displaystyle \frac{ P }{ ρg }+\displaystyle \frac{ v^2 }{ 2g }+h=H$
$ρ$ [kg/m3]:水の密度
$g$ [m/s2]:重力加速度
$P$ [Pa]:B点の圧力 (水圧)
$v$ [m/s]:B点の水の流れる速度 (流速)
$h$ [m]:B点の高さ
$H$ [m]:A点の高さ
電験三種-電力の過去問解説:パスカルの原理とベルヌーイの定理
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の電力科目で出題された問題です。
1999年(平成11年)問2
水力発電所の水圧管内における単位面積当たりの水が保有している運動エネルギー[J/m3]を表す式といて、正しいものは次のうちどれか。ただし、水の速度は水圧管の同一断面積において管路方向に均一とする。また、ρ は水の密度[kg/m3]、v は水の速度[m/s]を表す。
(1) $\displaystyle \frac{ 1 }{ 2 }ρ^2v^2$ (2) $\displaystyle \frac{ 1 }{ 2 }ρ^2v$ (3) $2ρv$ (4) $\displaystyle \frac{ 1 }{ 2 }ρv^2$ (5)$\displaystyle\sqrt{ 2 ρv} $
1999年(平成11年)問2 過去問解説
水の質量を m[kg]体積を V[m3]とすれば、水圧管中の運動エネルギー J[J/m3]は
$J=\displaystyle \frac{ 1 }{ 2 }mv^2=\displaystyle \frac{ 1 }{ 2 }ρVv^2$
単位体積当たりのエネルギーは
$J=\displaystyle \frac{ 1 }{ 2 }ρv^2[J/m3]$
答え (4)
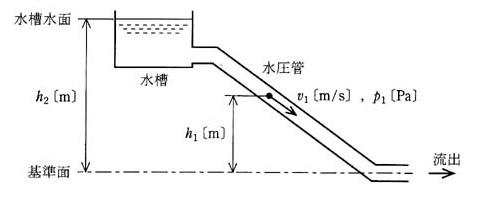
2004年(平成16年)問2
図において、基準面から h1[m]の高さにおける水管中の流速を v1[m/s]、圧力を p1[Pa]、水の密度を ρ[kg/m3]とすれば、質量 m[kg]の流水が持っているエネルギーは、位置のエネルギー mgh1[J]、運動のエネルギー( ア )[J]及び圧力によるエネルギー( イ )[J]である。これらのエネルギーの和は、エネルギー保存の法則により、最初に水が持っていた( ウ )に等しく、高さや流速が変化しても一定となる。これを( エ )という。ただし、管路には損失がないものとする。
上記記述中の空白箇所( ア )、( イ )、( ウ )及び( エ )に記入する語句又は式として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | $\displaystyle \frac{ 1 }{ 2 }m{v_1}^2$ | $m\displaystyle \frac{ p_1 }{ ρ }$ | 位置エネルギー | ベルヌーイの定理 |
| (2) | $m{v_1}^2$ | $m\displaystyle \frac{ ρ }{ p_1 }$ | 位置エネルギー | パスカルの原理 |
| (3) | $\displaystyle \frac{ 1 }{ 2 }m{v_1}^2$ | $\displaystyle \frac{ p_1 }{ ρg }$ | 運動エネルギー | ベルヌーイの定理 |
| (4) | $\displaystyle \frac{ 1 }{ 2 }mv_1$ | $m\displaystyle \frac{ p_1 }{ ρ }$ | 運動エネルギー | パスカルの原理 |
| (5) | $\displaystyle \frac{ 1 }{ 2 }\frac{ {v_1}^2 }{ g }$ | $\displaystyle \frac{ p_1 }{ ρg }$ | 圧力によるエネルギー | ベルヌーイの定理 |
2004年(平成16年)問2 過去問解説
図において、基準面から h1[m]の高さにおける水管中の流速を v1[m/s]、圧力を p1[Pa]、水の密度を ρ[kg/m3]とすれば、質量 m[kg]の流水が持っているエネルギーは、位置のエネルギー mgh1[J]、運動のエネルギー( $\displaystyle \frac{ 1 }{ 2 }m{v_1}^2$ )[J]及び圧力によるエネルギー( $m\displaystyle \frac{ p_1 }{ ρ }$ )[J]である。これらのエネルギーの和は、エネルギー保存の法則により、最初に水が持っていた( 位置エネルギー )に等しく、高さや流速が変化しても一定となる。これを( ベルヌーイの定理 )という。ただし、管路には損失がないものとする。
答え(1)
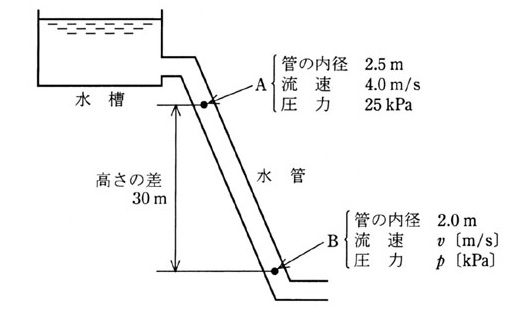
2006年(平成18年)問12
図の水管内に水が充満して流れている。点Aでは管の内径 2.5[m]で、これより 30[m]低い位置にある点Bでは内径 2.0[m]である。点Aでは流速 4.0[m/s]で圧力は 25[kpa]と計測されている。このときの点Bにおける流速 v[m/s]と圧力 p[kpa]に最も近い値を組み合わせたのは次のうちどれか。
なお、圧力は水面との圧力差とし、水の密度は 1.0×103[kg/m3]とする。
| 流速 $v$[m/s] | 圧力 $p$[kpa] | |
| (1) | 4.0 | 296 |
| (2) | 5.0 | 296 |
| (3) | 5.0 | 307 |
| (4) | 6.3 | 307 |
| (5) | 6.3 | 319 |
2006年(平成18年)問12 過去問解説
B点の位置水頭を基準にすると、A点の水頭はベルヌーイの定理より
$\displaystyle \frac{ 25×10^3 }{ 1000×9.8 }+\displaystyle \frac{ 4^2 }{ 2×9.8 }+30≒33.36$[m]
質量保存の法則より「A点の流量=B点の流量」ですので、
$\displaystyle \frac{ π×2.5^2 }{ 4 }×4.0=\displaystyle \frac{ π×2.0^2 }{ 4 }×v$
$v=6.3$[m/s]
B点の水頭はベルヌーイの定理より
$\displaystyle \frac{ P}{ 1000×9.8 }+\displaystyle \frac{ 6.3^2 }{ 2×9.8 }+0≒33.36$[m]
$P=307000$
答え (4)
電験三種の電力科目に出題される「水力発電所」のページ
- 水力発電所のダムと水路
- パスカルの原理とベルヌーイの定理
- 河川の流量と流況曲線
- 水力発電所の仕組み(衝動水車と反動水車)
- 水力発電所と揚水発電所の出力






