すべての計測器の選定に共通なことですが、測定には目的が重要です。電流計では、次に挙げるような測定目的を正しく理解することが必要です。
- 直流、交流、高周波の別
- どの程度の電流や電圧を計測するのか
- 測定値にどのような精度が要求されているのか
このページでは、初心者の方でもわかりやすいように、電流や電圧の測定計器についてやさしく解説しています。
電圧計と電流計の違い
電圧計と電流計の説明を見ていると、それぞれまったく違う原理の計器のように感じるかも知れませんが、アナログ計器としてもっとも多く利用されている可動コイル形の電圧計と電流計では、指示計器そのものはまったく同じものが使えます。
なぜ、内部抵抗の高い電圧計と内部抵抗の低い電流計が同じ計器で測定することができるのかといいますと、電圧計では図1(a)のように抵抗を直列に接続し、電流計は図1(b)のように抵抗を並列に接続しています。
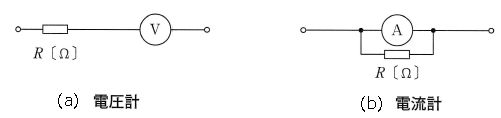
10〔kΩ /V〕の電圧計を例にしてみると、電圧と抵抗値がわかれば、電流は次の式で計算できますから、この電圧計にどれだけの電流が流れると最大の振れになるかがわかります。
$I=\displaystyle\frac{V}{R}= \displaystyle\frac {1}{10×10^3}=10^{-4}$ 〔A〕
この計器のコイル抵抗が1〔kΩ〕であると仮定すると、 $10^{-4}$ 〔A〕 の電流が流れたときの電圧は、
$V=IR=10 ^{-4} × 10^3=10^{-1}$〔V〕$=0.1$〔V〕
このことから、この計器はフルスケールが0.1〔V〕の電圧計であるとともに、 $10^{-4}$ 〔A〕の電流計でもあることがわかります。
測定範囲の拡大
0.1〔V〕の電圧や $10^{-4}$〔A〕の電流のような小さな値を測定することもありますが、 もっと高い電圧や大きな電流を測定することが多いです。そこで、測定範囲の拡大をする方法について考えてみます。
電圧計の測定範囲の拡大と倍率器
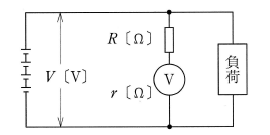
0.1〔V〕の電圧計では実用的ではありません。それ以上の電圧を計測できるようにするには、図1(a)のように直列抵抗$R$を接続します。計器自体の抵抗は1〔kΩ 〕ですから、 9〔kΩ 〕を直列に接続すると合成抵抗は10〔kΩ 〕になります。
計器に $10^{-4}$〔A〕の電流を流したときに、最大の振れとなるのですから、この場合、直列抵抗と計器全体の電圧降下$V$は、
$V=IR=100×10^{-6}×10×10^3=1$ 〔V〕
9〔kΩ 〕の抵抗を直列に接続することで電圧の測定範囲を10倍にすることができます。直列抵抗を99〔kΩ 〕にすると、合成抵抗は100〔kΩ〕になり、10〔V〕が測定できる電圧計になります。
この電圧計では、フルスケールを1〔V〕にすると内部抵抗は10〔kΩ 〕になり、10〔V〕では100〔kΩ〕と1〔V〕あたり10〔kΩ〕になりますから、この電圧計の内部抵抗は、10〔kΩ/V〕と表すことができます。
このように、直列に抵抗を接続することで測定範囲を何倍かにすることができますから、この抵抗を「倍率器」といいます(図2)。
計器自体の測定電圧と測定したい電圧との比率を$m$としますと、計器自体の内部抵抗が$r$〔Ω〕であれば、倍率器の抵抗値$R$は次の式で計算できます。
$R=(m -1)r$ 〔Ω〕
電流計の測定範囲の拡大と分流器
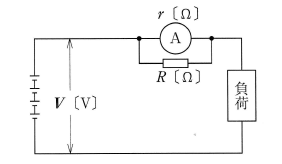
電流計で測定範囲を拡大するには、図1(b)のように、計器に対して並列に抵抗を接続して、電流を分流(バイパス)させます。計器自体の内部抵抗γは1〔kΩ 〕です。
これに分流抵抗$R=\displaystyle\frac{r}{9}≒ 111.11$〔Ω〕を接続すると、合成抵抗$R_0$は100〔Ω〕になります。
$R_0=\displaystyle\frac{rR}{r+R}=\displaystyle\frac{ 1000×\displaystyle\frac{1000}{9} }{1000+\displaystyle\frac{1000}{9}}=100$ 〔Ω〕
この計器にフルスケールの $10^{-4}$ 〔A〕 を流すと、内部抵抗の$\displaystyle\frac{1}{9}$の抵抗値の分流抵抗$R$には、9倍の $9×10^{-4}$ 〔A〕 が流れ、全体としての電流は1〔mA〕になります。
このように、電流計では並列に抵抗を接続して電流を分流させることで、測定範囲を拡大することができますから、この抵抗を「分流器〕といいます(図3)。
計器自体の測定電流と測定したい電流との比率を$m$としますと、計器自体の内部抵抗が$r$〔Ω〕であれば、分流器の抵抗値$R$は次の式で計算することができます。
$R=\displaystyle\frac{r}{m-1}$
倍率器と分流器の誤差
倍率器の抵抗値計算式や分流器の抵抗値計算式を見てわかることは、これらの外付け抵抗の誤差は、測定値の誤差になります。分流器はそれぞれの計器に対応したものが計器メーカーから発売されていますから、高価ではありますが、それを使わなければなりません。したがって、計算どおりの抵抗が手元にあっても、それを使うと誤差が大きくなります。
電圧計と電流計を同時に使う場合の誤差
電圧計と電流計を同時に使う場合、図4の(a)と(b)の接続法が考えられます。
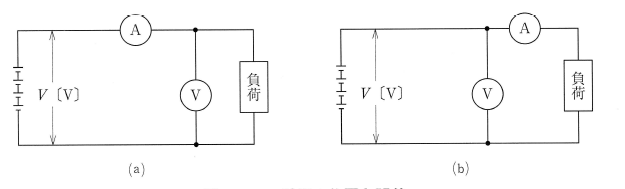
図4 (a)では、電圧計が負荷に対して並列に接続されていますから、電圧計は負荷の電圧を正しく測定できるのですが、電流計には負荷に流れる電流と電圧計に流れる電流の両方が指示され、電流測定誤差の原因になります。
図4 (b)では、電流計は負荷の電流を正しく測定できるのですが、電圧計は負荷と電流計の両方の電圧を指示してしまいますから、電圧測定誤差の原因になります。
どちらにしても、誤差が発生するのは止むを得ないことなのですが、負荷に流れる電流が大きくて、電圧計に流れる電流よりも十分に大きいときは(a)の接続法、逆に負荷に流れる電流が小さくて電圧計の電流が無視できないときには(b)の接続法を適用すると誤差を少なくすることができます。



