すべての計測器の選定に共通なことですが、測定には目的が重要です。電圧計では、次に挙げるような測定目的を正しく理解することが必要です。
- 直流、交流、高周波の別
- どの程度の電圧や電流を計測するのか
- 測定値にどのような精度が要求されているのか
このページでは、初心者の方でもわかりやすいように、電圧と電流の測定計器についてやさしく解説しています。
電圧計の選定方法
電圧計で測定する電圧が直流の場合は、直流用電圧計を使うのですが、直流電圧には正負(十,一)の極性がありますから、逆にしてはいけません。交流の測定では、極性はありませんが、交流電圧計を使わなければなりません。周波数が1〔Hz〕でも、100〔MHz〕でも、交流には違いありませんから、交流電圧計であれば、すべて測定できると考えるのは間違いです。一般的な交流電圧計は、正弦波の50~ 60〔Hz〕の商用周波数の交流を測定するための計器です。
非常に低い周波数の電圧を測定すると、アナログ計器では指針がふらふらと揺れて読取りが困難になります。ディジタル計器では表示する値がバラバラになります。高い周波数では、表示が実際の値よりも大きくなったり、小さくなったりして誤差が大きくなります。
これらに加えて,以下のような測定環境や使用条件などを配慮しなければなりません。
- 同じ箇所を連続的に測定するのか、複数箇所を移動して測定するのか
- 測定中に計器を見ることができるのか、見えないような状況なのか
同じ場所を連続的に測定する場合は,測定箇所が固定していますから制限はありませんが,移動して測定する場合には,携帯に便利な小型のものが便利です。ディジタル計器であれば電源を内蔵しているものでなければなりません。測定場所が,測定者の位置と離れていて,測定値が読み取れない場合は測定値を固定した後で手元に計器を持ってきて読み取ることができる計器を使う必要もあります。
電圧測定の要領
回路の電圧を測定するときは、図のように、回路に対して並列に電圧計を接続します。並列に接続するのですから、電圧計には電流が流れます。もし、抵抗が低いと、電圧計に大きな電流が流れて無駄な電力を消費するだけでなく、誤差が大きくなります。
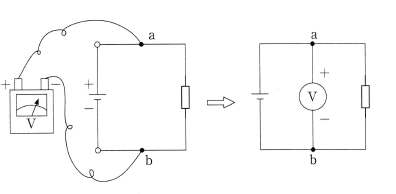
電圧計の内部抵抗の影響による誤差
目盛板に電圧計の内部抵抗の表示がされているタイプ電圧計があります。直接抵抗値を表示する他に、10〔kΩ/V〕と表示されることがあります。
これは、レンジを切り替えられる電圧計の内部抵抗の割合を示しているもので、フルスケールが10〔V〕であれば、内部抵抗は100〔kΩ〕になり、100〔V〕であれば、内部抵抗は1〔MΩ〕になります。
内部抵抗が100〔kΩ〕の電圧計を使って、図の回路で$R_2$の電圧を測った場合の誤差について考えます。$R_1=R_2=100$〔Ω〕であれば、電圧計のないときは、$R_2$の電圧は電源電圧の半分の3〔V〕です。電圧測定時は、電圧計の内部抵抗の$R_3$=100〔kΩ〕が$R_2$に対して並列に入り、$R_2$と$R_3$の合成抵抗は99.9〔Ω〕になります。
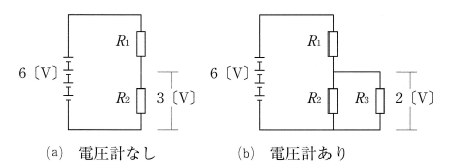
この例では、測定値を計算すると2.9985〔V〕になり、0.05%低下するのですが、実用上は問題がないと考えられます。したがって、この例では、電圧計の内部抵抗による誤差は無視できます。
$R_1$=$R_2$=100〔kΩ〕の例を考えますと,電圧計のないときの電圧$V_1$は、電源電圧の半分の3〔V〕になります。
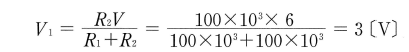
しかし、測定するときには電圧計の内部抵抗の$R_3$=100〔kΩ〕が$R_2$に対して並列に入りますから、$R_2$と$R_3$の合成抵抗$R_{23}$は50〔kΩ〕になり、このとき測定電圧$V_2$は2〔V〕に低下してしまいます。
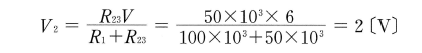
これが、電圧計の内部抵抗で誤差が発生する理由です。したがって、$R_1$や$R_2$ のような電気回路を構成している抵抗値に対して、電圧計の内部抵抗は十分高くなければなりません。
ディジタル電圧計の内部抵抗は、測定レンジにかかわらず10〔MΩ〕程度と非常に高いのですが、アナログ電圧計では、5~ 50〔kΩ /V〕程度のものが多いので、100〔kΩ〕~ 1〔MΩ〕程度の抵抗を多く使うMOSFETやオペアンプなどのインピーダンスの高い回路では、ディジタル計器しか使えないと考えるほうが無難です。もし、内部抵抗の小さな計器を使いますと、入力・出力電圧が変化して、動作状態が変化してしまう可能性があります。
アナログ計器を購入する場合は、できるだけ内部抵抗の高いものを購入したいと思うでしょうが、このような計器は感度の良いものなので、価格は高く、壊れやすいのが欠点です。
電流測定の要領
電流測定は、図1のように回路に対して直列に電流計を挿入して計測します。もし、電流計を電圧計のように回路に対して並列に接続すると非常に大きな電流が流れ、電流計を壊してしまいますから注意が必要です。
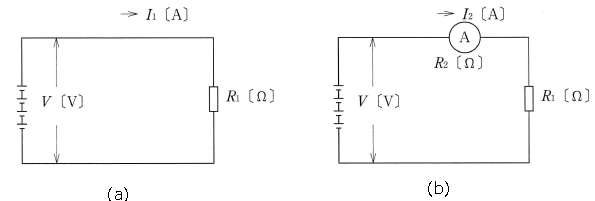
電流計の内部抵抗の影響による誤差
図1(a)は、電流計を入れない場合の回路です。この回路の電流$I_1$〔A〕と電流計を入れた図1(b)の電流$I_2$〔A〕の変化から、電流計の内部抵抗と測定誤差がどのように関係しているかを考えます。
次の二つの式から$I_1$〔A〕と$I_2$〔A〕の比率を式で表すと、
$I_1=\displaystyle\frac{V}{R_1}$〔A〕 $I_2=\displaystyle\frac{V}{R_1+R_2}$〔A〕
$\displaystyle\frac{I_2}{I_1}=\displaystyle\frac{R_1}{R_1+R_2}$
例として、$R_1$=100〔Ω〕、$R_2=0.01$〔Ω〕$=1$〔mΩ〕とすると、
$I_2=\displaystyle\frac{100}{100+0.01}≒0.99990$〔A〕
この場合の誤差は、0.01%ですので、無視しても差し支えありません。しかし、$R_1$=0.1〔Ω〕、$R_2=0.01$〔Ω〕$とすると、
$I_2=\displaystyle\frac{0.1}{0.1+0.01}≒0.909$〔A〕
この場合の誤差は、約9.1%となり、非常に大きくなってしまいます。別の見方をしますと、負荷抵抗に対する電流計の内部抵抗の比率が大きいと、誤差が大きくなるということです。
つまり、内部抵抗が大きいと電圧降下が大きくなって誤差が増えるとともに、無駄な電力も消費することになります。



