変圧器の原理と構造

このページでは、変圧器の原理と構造について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された変圧器の原理と構造の過去問題の解き方も解説しています。

変圧器の原理と構造
変圧器の理論
1. 理想変圧器の電圧・電流・磁束
2. 実際の変圧器の電圧・電流・磁束
電験三種－機械（変圧器）過去問

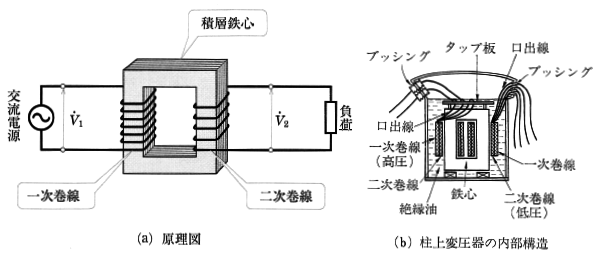
変圧器の原理と構造

変圧器は、図1(a)に示すように、鉄心に巻線を巻いたもので、電源側を一次巻線、負荷側を二次巻線といいます。一次巻線に電圧 $\dot{V}_1$［V］を加えると、相互誘導作用の働きによって、二次巻線に電圧 $\dot{V}_2$［V］が発生します。

一般に、電力用の変圧器は、鉄心と巻線の部分を容器に収め、絶縁油に浸されています。鉄心には鉄損の少ない、すぐれた磁化特性をもった電磁鋼板を積み重ねて用いています。巻線は電気回路を構成し、鉄心は磁気回路を構成しています。図1(b)は柱上変圧器の構造図の例です。

内鉄形と外鉄形

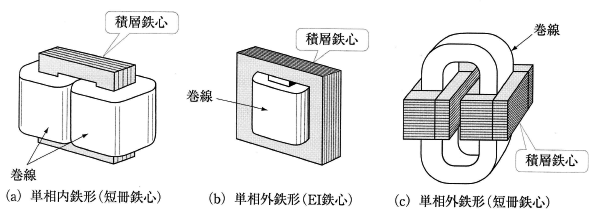
鉄心に巻線を巻く場合、構造的にみて図2(a),(b)に示すような内鉄形と外鉄形に分けられます。内鉄形は構造上絶縁が容易ですので、高電圧・大容量に適し、外鉄形は低電圧・大電流の変圧器に用いられています。しかし、最近では技術の進歩によって、この区別は明確でなくなっています。

鉄心

変圧器の鉄心には、飽和磁束密度と透磁率が大きく、鉄損の少ない材料が用いられます。一般に広く用いられている材料は、ヒステリシス損を減少させるためにけい素を含有させ、その含有量が3.5%程度のG級電磁鋼板です。G級電磁鋼板は、方向性電磁鋼帯で、一方向だけ磁束を通しやすい性質があります。また、1枚1枚の電磁鋼板の表面に施してある絶縁皮膜が、温度上昇の一因となる渦電流が流れるのを防ぐ働きをしています。

占積率

電磁鋼板の表面は、絶縁皮膜でおおわれているので、図2(a),(b)に示すように、鋼板を積み重ねて積層鉄心とする場合には、磁束を通す鉄心の有効断面積と、実際に占める断面積とは異なります。その比を占積率といい、一般には96%程度です。

鉄心の構造

ふつう変圧器の鉄心には、短冊鉄心とよばれる短冊形電磁鋼板を積み重ねた積層鉄心が用いられます。その組み立ては図3(a)に示すようにして行います。鉄心の接続には、図(b)のように継目が1か所にならないように重ねていきます。これを重ね接続といいます。打ち抜き鉄心は、通信機器用小形変圧器の鉄心に用いられ、図(c)に示すようなEI形が多いです。巻鉄心は、継目のない方向性電磁鋼帯を巻いた鉄心で、短冊鉄心に比べて、励磁電流が小さく、鉄心も軽くできます。おもに柱上変圧器などの小形変圧器に用いられます。図(d)は巻鉄心の例です。鉄心全体を合成樹脂で接着したあと2か所で切断し、巻線をはめ込んだのち、圧力を加えて突合せ接続にして用いるもので、カットコアともよばれています。

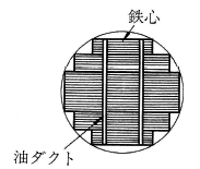
変圧器は鉄損や銅損などにより発熱するので、本体を油中に浸して冷却しているものが多いです。大容量の変圧器では、鉄心中にも油が通るようにするため、図4に示すように、鉄心中に油ダクトを設けているものがあります。

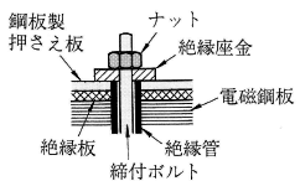
積層鉄心を一体とするためには、図5に示すように、押さえ板やボルトを通して渦電流が流れないように絶縁した締付ボルトで固定します。また、電磁鋼板を接着剤で張り合わせて、ボルトの数を少なくする方法もとられています。

巻線

巻線には、軟銅線が用いられ、形状によって丸線と平角線があります。小容量の変圧器では、細い丸線が用いられ、多くの場合はホルマール線を使用しています。中容量および大容量の変圧器では、平角裸銅線に絶縁を施したものが用いられています。

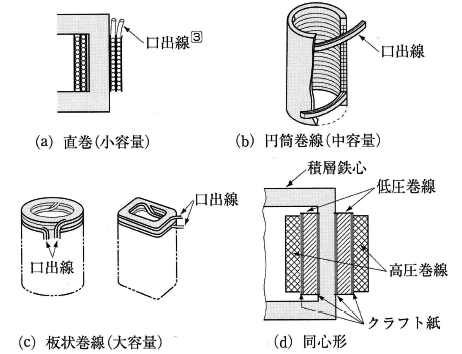
巻線の方法には、小容量の変圧器では、図6(a)に示すように、鉄心に絶縁を施し、その上に巻線を直接巻きつける方法がありますが、容量が大きくなると作業が困難になります。中容量および大容量の変圧器では、図6(b),(c)に示す円筒巻線や板状巻線として、これを鉄心にはめ込む方法がとられています。

このような巻線を鉄心に対して配置する場合には、図(d)に示すように、一次巻線と二次巻線の間や、巻線と鉄心の間に絶縁を施します。図(d)の同心形では、クラフト紙を巻いてフェノール樹脂で固めた絶縁筒などが用いられています。

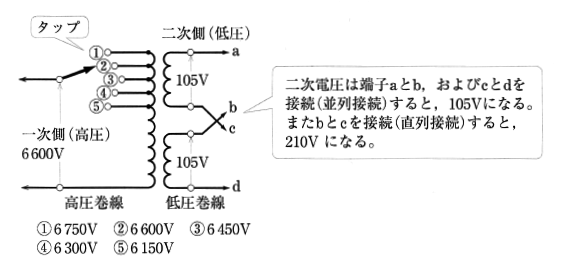
柱上変圧器の一次巻線には、二次電圧の調整のために、図7のようなタップが設けられています。これは、二次側の負荷の変動に対して二次側の出力電圧を一定に保つためのもので、必要に応じてタップの位置をつなぎ換えるようにしています。

変圧器の理論

理想変圧器の電圧・電流・磁束

一次・二次巻線の抵抗や鉄損を無視した変圧器を理想変圧器といいます。理想変圧器は、実際につくることはできませんが、変圧器の動作を知るうえで重要です。

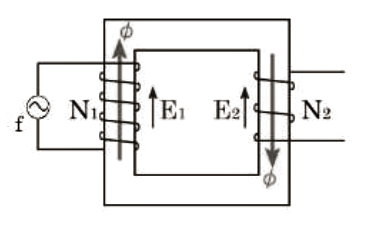
図8において、スイッチＳを開いているとき一次巻線(巻数 $N_1$ )に電圧 $\dot{V}_1$［V］が加わると、鉄心中には大きさと向きが周期的に変化する磁束 $ϕ$［Wb］が生じます。そのため、一次巻線および二次巻線(巻数 $N_2$ )には、起電力 $\dot{E}_1$［V］，$\dot{E}_2$［V］が誘導されます。

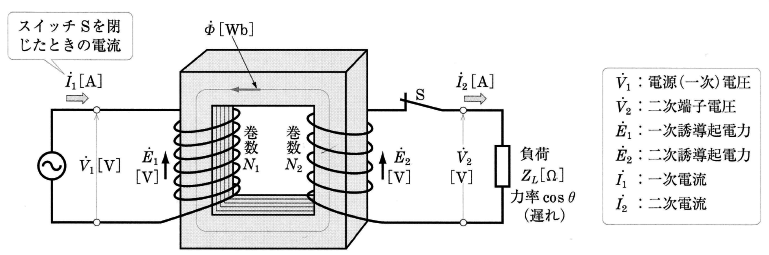
次に、図8において、スイッチＳを閉じると、起電力 $\dot{E}_2$［V］によって、二次回路には電流 $\dot{I}_2$［A］が流れます。また、電流 $\dot{I}_2$［A］によって起磁力 $N_2\dot{I}_2$［A］が生じ、磁束 $\dot{ϕ}$［Wb］は減少しようとしますが、$\dot{ϕ}$ の最大値 $ϕ_m$［Wb］が一定値を保つように一次側には電源から一次電流 $\dot{I}_1$［A］が流入して、$N_2\dot{I}_2$［A］の起磁力を打ち消します。すなわち、$\dot{I}_1$［A］と $\dot{I}_2$［A］との間には、$N_1\dot{I}_1=N_2\dot{I}_2$ の関係があります。ここで、$\dot{E}_1$［V］を一次誘導起電力、$\dot{E}_2$［V］を二次誘導起電力、$\dot{I}_1$［A］を一次電流、$\dot{I}_2$［A］を二次電流といいます。

負荷時の電圧・電流・磁束

図8においてスイッチSを閉じた場合の電圧・電流の関係をベクトル図で示すと、図9(b)のようになります。すなわち、一次側に加える電圧 $\dot{V}_1$［V］より $\displaystyle\frac{π}{2}$［rad］位相の遅れた磁束 $\dot{ϕ}$［Wb］が生じ、その磁束によって、それより $\displaystyle\frac{π}{2}$［rad］位相の進んだ起電力 $\dot{E}_1$［V］，$\dot{E}_2$［V］が、一次巻線および二次巻線に誘導されます。

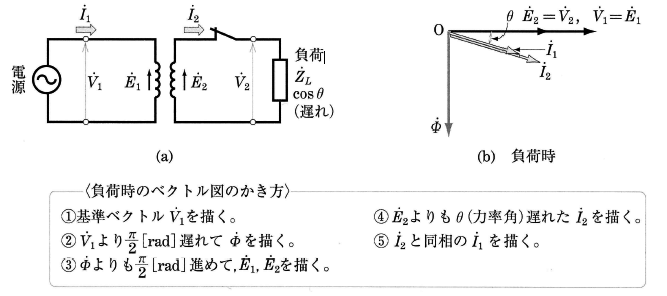
この場合、鉄心中の磁束の最大値を $ϕ_m$［Wb］とすれば、次の関係がなりたちます。

$E_1=\displaystyle\frac{1}{\sqrt{2}}ϕ_mωN_1=4.44fN_1ϕ_m$ … (1)

$E_2=\displaystyle\frac{1}{\sqrt{2}}ϕ_mωN_2=4.44fN_2ϕ_m$ … (1)’

なお、一次回路と二次回路の電圧の比および電流の比は次の式で表されます。

$\displaystyle\frac{E_1}{E_2}=\displaystyle\frac{N_1}{N_2}=\displaystyle\frac{I_2}{I_1}=a$ … (2)

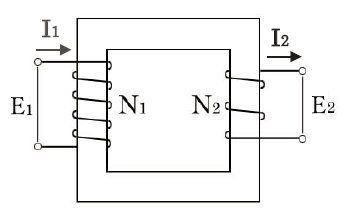
ここで、巻線比 $\displaystyle\frac{N_1}{N_2}=a$ を変圧器の巻線比といいます。

実際の変圧器の電圧・電流・磁束

実際の変圧器では、一次・二次巻線には抵抗があるため銅損が生じます。また、鉄心の透磁率は無限大でないので、磁束をつくるため電流が必要となります。この電流を励磁電流といいます。これによって、鉄心中には鉄損が生じます。また、一次巻線の電流による磁束は、すべて二次巻線と鎖交するとは限りません。ここでは、これらのことを考慮して、電圧，電流について考えてみます。

励磁電流

実際の変圧器では、一次巻線に交流電圧を加えると、鉄心の磁気飽和現象やヒステリシス現象が生じるので、励磁電流は図11(a)の ${i_o}’$［A］のような非正弦波交流となります。この ${i_o}’$［A］と周波数および実効値が等しい正弦波交流(等価正弦波) ${i_o}$［A］で表して取り扱います。${i_o}$ の位相は、鉄損のために、図(b)のように磁束 $\dot{ϕ}$ より $α_o$ だけ進むことになります。この $α_o$ を鉄損角といいます。

図(a)の $v_1$［V］，$e_1$［V］，$i_o$［A］をベクトル図で示すと、図(b)となります。励磁電流 $\dot{I}_o$［A］は、一次電圧 $\dot{V}_1$［V］と同相である成分 $\dot{I}_{ow}$［A］、および $\dot{V}_1$ よりも位相が $\displaystyle\frac{π}{2}$［rad］遅れている成分 $\dot{I}_{ol}$［A］に分けて考えることができます。$\dot{I}_{ow}$［A］を鉄損電流といい、$\dot{I}_{ol}$［A］を磁化電流といいます。

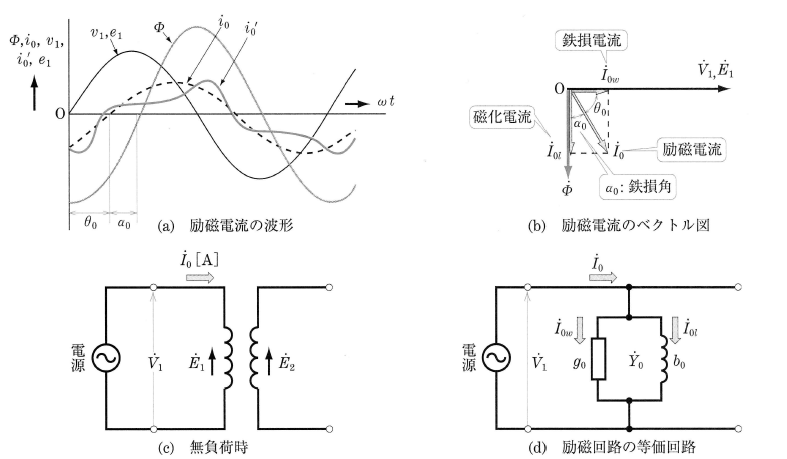
図11(c)は無負荷時の励磁回路ですが、この励磁回路に、$\dot{I}_{ow}$［A］，$\dot{I}_{ol}$［A］の二つの電流が流れているとすれば、その等価回路は、図(d)で示されます。$\dot{Y}_o$［S］を励磁アドミタンス、$g_o$［S］を励磁コンダクタンス、$b_o$［S］を励磁サセプタンスといいます。この回路は、変圧器の励磁回路の等価回路です。

以上のことを式で示すと、次のようになります。

$cosθ_o=\displaystyle\frac{I_{ow}}{I_o}=\displaystyle\frac{I_{ow}V_1}{I_oV_1}=\displaystyle\frac{鉄損}{I_oV_1}=cos(\displaystyle\frac{π}{2}-α_o)=sinα_o$ … (3)

$\dot{Y}_o=g_o-jb_o=\displaystyle\frac{\dot{I}_o}{\dot{V}_1}$ … (4)

$g_o=\displaystyle\frac{I_{ow}}{V_1}=\displaystyle\frac{I_{ow}V_1}{{V_1}^2}=\displaystyle\frac{鉄損}{{V_1}^2}$ … (5)

$b_o=\displaystyle\frac{I_{ol}}{V_1}=\displaystyle\frac{I_{ol}V_1}{{V_1}^2}=\displaystyle\frac{無効電力}{{V_1}^2}$ … (6)

巻線の抵抗と漏れリアクタンス

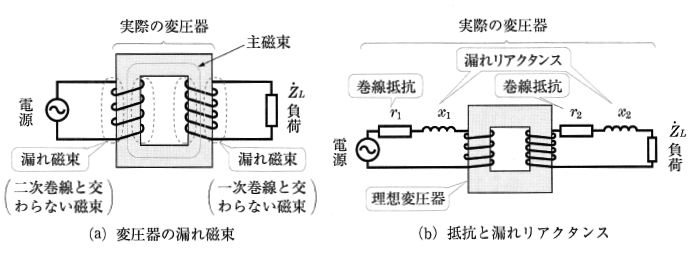
実際の変圧器では、一次巻線も二次巻線もそれぞれ抵抗 $r_1$［Ω］，$r_2$［Ω］をもっています。また、図12(a)のように、一次・二次巻線を貫く主磁束のほかに漏れ磁束があります。漏れ磁束の効果は、図(b)のように、$x_1$［Ω］，$x_2$［Ω］で示すリアクタンスとして作用します。これを漏れリアクタンスといいます。

電験三種－機械（変圧器）過去問

2006年（平成18年）問6　過去問解説

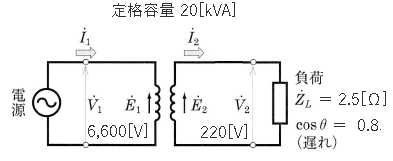
定格容量 20［kVA］、定格一次電圧 6,600［V］、定格二次電圧 220［V］の単相変圧器がある。この変圧器の一次側に定格電圧の電源を接続し、二次側に力率が 0.8、インピーダンスが 2.5［Ω］である負荷を接続して運転しているときの一次巻線に流れる電流を $I_1$［A］とする。定格運転時の一次巻線に流れる電流を $I_{1r}$［A］とするとき、$\displaystyle\frac{I_1}{I_{1r}}×100$［%］の値として、最も近いのは次のうちどれか。
ただし、一次・二次巻線の銅損、鉄心の鉄損、励磁電流及びインピーダンス降下は無視できるものとする。

(1) 89　(2) 91　(3) 93　(4) 95　(5) 97

2006年（平成18年）問6　過去問解説

負荷 $Z_L=2.5$［Ω］を接続したときに、2次側に流れる電流を $I_2$とすると、

$I_2=\displaystyle\frac{V_2}{Z_L}=\displaystyle\frac{220}{2.5}=88$［A］

一次回路と二次回路の電圧の比は、

$\displaystyle\frac{V_1}{V_2}=\displaystyle\frac{N_1}{N_2}=\displaystyle\frac{I_2}{I_1}=a$

$a=\displaystyle\frac{6600}{220}=30$

したがって、負荷 $Z_L$［Ω］を接続したときの、1次側に流れる電流を $I_1$は、

$I_1=\displaystyle\frac{I_2}{a}=\displaystyle\frac{88}{30}≒2.93$［A］

定格時の一次電流 $I_{1r}$［A］は、定格容量を $S_n$［kVA］とすると、

$S_n=V_1I_{1r}$
$20=6.6×I_{1r}$
$I_{1r}≒3.03$［A］

したがって、$\displaystyle\frac{I_1}{I_{1r}}×100$［%］は、

$\displaystyle\frac{I_1}{I_{1r}}×100=\displaystyle\frac{2.93}{3.03}×100≒97$［%］

答え (5)

2008年（平成20年）問7

一次巻線抵抗、二次巻線抵抗、漏れリアクタンスや鉄損を無視した磁気飽和のない理想的な単相変圧器を考える。この変圧器の鉄心中の磁束の最大値を $ϕ_m$［Wb］、一次巻線の巻数を $N_1$、この変圧器に印加される正弦波電圧の（　ア　）を $V_1$［V］、周波数を $f$［Hz］とすると、$ϕ_m$ は次式から求められる。

$ϕ_m=$（　イ　）・$\displaystyle\frac{V_1}{fN_1}$［Wb］

この磁束により変圧器の二次端子に二次誘導起電力 $V_2$［V］が生じる。
一次巻線の巻数 $N_1$、二次巻線の巻数 $N_2$ がそれぞれ 2550，85の場合、この変圧器の一次側に 6300［V］の電圧を印加すると、二次側に誘起される電圧は（　ウ　）［V］となる。
変圧器二次端子に 7［Ω］の抵抗負荷を接続した場合の一次電流 $I_1$、二次側電流 $I_2$ は、励磁電流を無視できるものとすると、それぞれ $I_1＝$（　エ　）［A］，$I_2=$（　オ　）［A］である。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。

	(ア)	(イ)	(ウ)	(エ)	(オ）
(1)	実効値	$\displaystyle\frac{\sqrt{2}}{2π}$	210	30	1.0
(2)	最大値	$\displaystyle\frac{2π}{\sqrt{2}}$	105	1.0	0.25
(3)	実効値	$\displaystyle\frac{\sqrt{2}}{2π}$	210	1.0	30
(4)	最大値	$\displaystyle\frac{1}{2π}$	105	15	30
(5)	実効値	$\displaystyle\frac{2π}{\sqrt{2}}$	105	1.0	0.25

(注) $\displaystyle\frac{\sqrt{2}}{2π}≒\displaystyle\frac{1}{4.44}$，$\displaystyle\frac{2π}{\sqrt{2}}≒4.44$，$\displaystyle\frac{1}{2π}≒0.159$ として計算する場合が多い。