第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題されるローレンツ力の向きと円運動について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題されたローレンツ力の向きと円運動の過去問題も解説しています。
荷電粒子に働くローレンツ力
フレミングの左手の法則は、電流を流した導体を永久磁石の磁界が及ぼす範囲中に置けば、電流が作る磁界と磁石が作る磁界との相互作用で力が発生するというものです。この力は「電磁力」といいます。
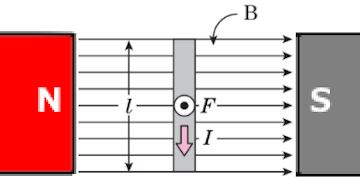
磁束密度 $B$[T]の一様な磁界のなかに、磁界と直角に長さ $l$[m]の導体を置いて、電流 $I$[A]流した時の導線が受ける電磁力の大きさ $F$[N]は次の式で求めることができます。
電流が磁界から受ける力の大きさ
$F=BIl=μHIl$[N]
$F$[N]:導体に働く力
$B$[T]:磁束密度
$I$[A]:導体に流れる電流
$l$[m]:導体の長さ
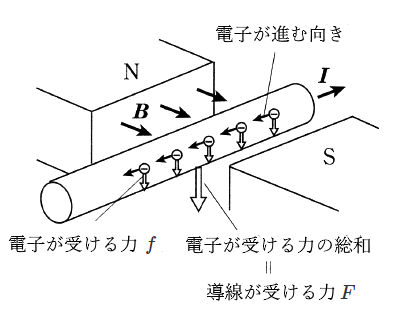
ここで、電子の電荷を $e$ [C]、平均の速さを $v$[m/s]、導体1m3あたりの電子数を $n$[個/m3]、導体の垂直断面積を $S$[m2]とすると、銅線に流れる電流 $I$[A]は次の式で求めることができます。
$I=enSv$[A]
したがって、フレミングの左手の法則は、次の式のように表すことができます。
$F=BIl=BenSvl=(evB)(nSl)$ [N]
$nSl$は、磁界中の導線内にある電子の総数ですので、電子1個当たりが受ける力 $f$[N]は、
$f=evB$ [N]
となります。この力は、電子だけではなく、すべての荷電粒子に適用できます。一般に、$q$[C]の電荷をもつ荷電粒子が、磁束密度 $B$[T]の一様な磁界と角度 $θ$ をなす向きに速さ $v$[m/s]で運動しているとき、磁界から受ける力の大きさは、次の式で求めることができます。
ローレンツ力を求める公式
$F=|q|vBsinθ$ [N]
$F$[N]:導体に働く力
$q$[C]:荷電粒子の電荷
$v$[m/s]:荷電粒子の速度
$B$[T]:磁束密度
この力を「ローレンツ力」といいます。ローレンツ力の向きは、電荷 $q$[C]の運動によって生じる電流が受ける力の向きと同じで、フレミング左手の法則の中指の方向と一致します。
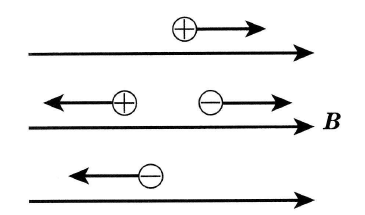
速度が磁界に平行なとき
荷電粒子が磁界に平行に運動しているときは、荷電粒子は磁界から力を受けません。つまり、ローレンツ力は 0 になり、荷電粒子は磁界に平行に等速運動を続けます。
速度が磁界に垂直なとき
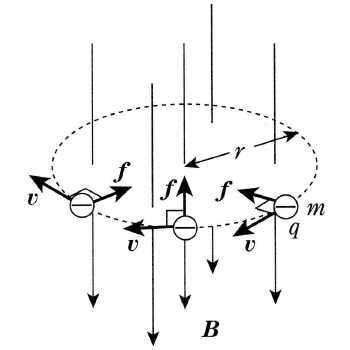
質量 $m$[kg]、電荷 $q$[C]の荷電粒子が磁束密度 $B$[T]の一様な磁界に垂直に、速さ $v$[m/s]で、入射する場合を考えます。
荷電粒子は、ローレンツ力を向心力として「等速円運動」を行います。この円の半径を $r$[m]とすると、向心力の大きさは次の式で求めることができます。
等速円運動の向心力を求める公式
$F=\displaystyle\frac{mv^2}{r}$[N]
$F$[N]:電子にはたらく力 (向心力)
$m$[kg]:電子の質量
$v$[m/s]:電子の速度
$r$[m]:電子が円運動をする時の円の半径
この向心力の大きさは、ローレンツ力と同じになるため、次の関係が成り立ちます。
$\displaystyle\frac{mv^2}{r}=evB$[N]
磁界中を磁束と垂直に電子が移動すると電子は 円運動 をしますが、このとき電子が一周するのにかかる時間 (周期) と角速度を求める式は次のようになります。
磁界中の電子が一周するのにかかる時間 (周期) と角速度を求める式
周期 $T=\displaystyle\frac{2πr}{v}=\displaystyle\frac{2πm}{qB}$
角速度 $ω=\displaystyle\frac{2π}{T}=\displaystyle\frac{v}{r}=\displaystyle\frac{qB}{m}$
$m$[kg]:電子の質量
$v$[m/s]:電子の速度
$r$[m]:電子が円運動をする時の円の半径
$q$[C]:電子の電荷
$B$[T]:磁束密度
このような円運動は、「サイクロトロン運動」といい、角速度 $ω$ は、「サイクロトロン角振動数」といいます。角速度および円運動の周期は、粒子の速さにも円運動の半径にも依存しません。
速度が磁界に任意の角度のとき
速度が磁界に任意の角度のときは、速度を磁界に平行な成分とに分けます。磁界に平行な速度成分は変化せず、垂直な速度成分は等速円運動を行います。この両者が合成されると、磁界に平行な「等速らせん運動]が起こります。
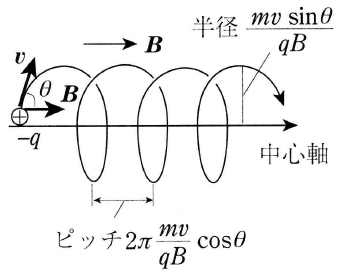
質量 $m$[kg]、電荷 $q$[C]の荷電粒子が磁束密度 $B$[T]の一様な磁界に垂直に、速さ $v$[m/s]で、$v$ と $B$ のなす角度が $θ$ で入射する場合を考えます。
$B$ に平行な速度成分:$v_{||}=vcosθ$(一定)
$B$ に垂直な速度成分:$v_{⊥}=vsinθ$(一定)
ローレンツ力:$F=qvBsinθ=qv_{⊥}B$(一定)
回転半径:$r=\displaystyle\frac{mv_{⊥}}{qB}=\displaystyle\frac{mvsinθ}{qB}$
となります。荷電粒子は、回転運動の1周期 $T$ の間に
$v_{||}T=2π\displaystyle\frac{mv}{qB}cosθ$
だけ、磁界に沿って進みます。これを「ピッチ」といいます。
電験三種-理論の過去問解説:ローレンツ力の向きと円運動
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2004年(平成16年)問11【電験理論の過去問題】
電流が流れている導体を磁界中に置くと、フレミングの( ア )の法則に従う電磁力を受ける。これは導体中を移動している電子が磁界から力を受け。結果として導体に力が働くと考えられている。
また、強さが一定の一様な磁界中に、磁界の方向と直角に電子が突入した場合は、電子の運動方向と常に( イ )方向の力を受け、結果として等速( ウ )運動をすることになる。このような力を( エ )という。
上記の記述の空欄箇所(ア),(イ),(ウ)及び(エ)に記入する語句として、正しいものを組合せたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 左手 | 直角 | 円 | ローレンツ力 |
| (2) | 右手 | 同 | 円 | マクスウェルの引張応力 |
| (3) | 左手 | 直角 | 直線 | ローレンツ力 |
| (4) | 左手 | 同 | 直線 | マクスウェルの引張応力 |
| (5) | 右手 | 直角 | 直線 | ローレンツ力 |
電流が流れている導体を磁界中に置くと、フレミングの( 左手 )の法則に従う電磁力を受ける。これは導体中を移動している電子が磁界から力を受け。結果として導体に力が働くと考えられている。
また、強さが一定の一様な磁界中に、磁界の方向と直角に電子が突入した場合は、電子の運動方向と常に( 直角 )方向の力を受け、結果として等速( 円 )運動をすることになる。このような力を( ローレンツ力 )という。
答え (1)
2007年(平成19年)問13【電験理論の過去問題】
真空中において磁束密度 $B$[T]の平等磁界中に、磁界の方向と直角に初速 $v$[m/s]で入射した電子は、電磁力 $F=$( ア )[N]によって円運動をする。
その円運動の半径を $r$[m]とすれば、遠心力と電磁力とが釣り合うので、円運動の半径は $r=$( イ )[m]となる。また、円運動の角速度は $ω=\displaystyle\frac{v}{r}$[rad/s]であるから、円運動の周期は $T=$( ウ )[s]となる。
ただし、電子の質量を $m$[kg]、電荷の大きさを $e$[C]とし、重力の大きさは無視できるものとする。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる式として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | $Bmev$ | $\displaystyle\frac{mv}{Be}$ | $\displaystyle\frac{2πm}{Be}$ |
| (2) | $Bev$ | $\displaystyle\frac{mv}{Be}$ | $\displaystyle\frac{2πm}{Be}$ |
| (3) | $Bmev$ | $\displaystyle\frac{v}{Be}$ | $\displaystyle\frac{2πm}{Be}$ |
| (4) | $Bev$ | $\displaystyle\frac{mv}{Be}$ | $\displaystyle\frac{2π}{Be}$ |
| (5) | $Bmev$ | $\displaystyle\frac{v}{Be}$ | $\displaystyle\frac{2π}{Be}$ |
真空中において磁束密度 $B$[T]の平等磁界中に、磁界の方向と直角に初速 $v$[m/s]で入射した電子は、電磁力 $F=$( $Bev$ )[N]によって円運動をする。
その円運動の半径を $r$[m]とすれば、遠心力と電磁力とが釣り合うので、円運動の半径は $r=$( $\displaystyle\frac{mv}{Be}$ )[m]となる。また、円運動の角速度は $ω=\displaystyle\frac{v}{r}$[rad/s]であるから、円運動の周期は $T=$( $\displaystyle\frac{2πm}{Be}$ )[s]となる。
答え (2)
2009年(平成21)問12【電験理論の過去問題】
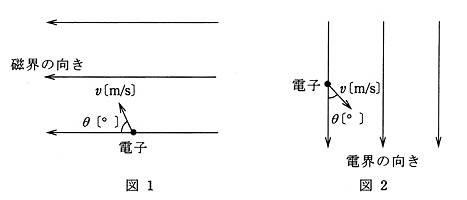
図1のように、真空中において強さが一定で一様な磁界中に、速さ $v$[m/s]の電子が磁界の向きに対して $θ$[°]の角度(0[°] < θ[°] < 90[°])で突入した。この場合、電子は進行方向にも磁界の向きにも( ア )方向の電磁力を常に受けて、その軌跡は、( イ )を描く。
次に、電界中に電子を置くと、電子は電界の向きと( ウ )方向の静電力を受ける。また、図2のように、強さが一定で一様な電界中に、速さ $v$[m/s]の電子が電界の向きに対してθ[°]の角度(0[°] < θ[°] < 90[°])で突入したとき、その軌跡は、( エ )を描く。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたものは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 反対 | らせん | 反対 | 放物線 |
| (2) | 直角 | 円 | 同じ | 円 |
| (3) | 同じ | 円 | 直角 | 放物線 |
| (4) | 反対 | らせん | 同じ | 円 |
| (5) | 直角 | らせん | 反対 | 放物線 |
図1のように、真空中において強さが一定で一様な磁界中に、速さ $v$[m/s]の電子が磁界の向きに対して $θ$[°]の角度(0[°] < θ[°] < 90[°])で突入した。この場合、電子は進行方向にも磁界の向きにも( 直角 )方向の電磁力を常に受けて、その軌跡は、( らせん )を描く。
次に、電界中に電子を置くと、電子は電界の向きと( 反対 )方向の静電力を受ける。また、図2のように、強さが一定で一様な電界中に、速さ $v$[m/s]の電子が電界の向きに対してθ[°]の角度(0[°] < θ[°] < 90[°])で突入したとき、その軌跡は、( 放物線 )を描く。
答え (5)
2012年(平成24)問12【電験理論の過去問題】
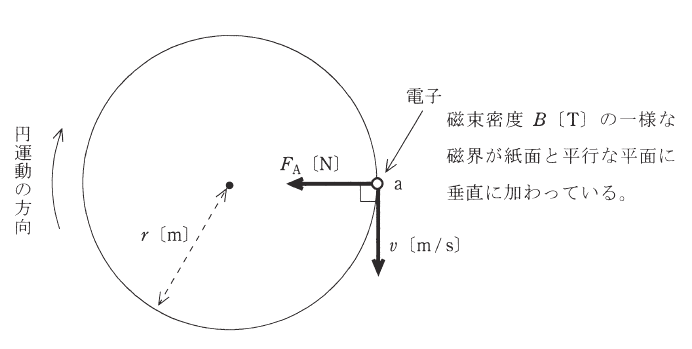
次の文章は、図に示す「磁界中における電子の運動」に関する記述である。
真空中において、磁束密度 $B$ [T] の一様な磁界が紙面と平行な平面の( ア )へ垂直に加わっている。ここで、平面上の点 a に電荷 $-e$ [C]、質量 $m_o$ [kg] の電子をおき、図に示す向きに速さ $v$ [m/s] の初速度を与えると、電子は初速度の向き及び磁界の向きのいずれに対しても垂直で図に示す向きの電磁力 $F_A$ [N] を受ける。この力のために電子は加速度を受けるが速度の大きさは変わらないので、その方向のみが変化する。したがって、電子はこの平面上で時計回りに速さ $v$ [m/s] の円運動をする。この円の半径を $r$ [m] とすると、電子の運動は、磁界が電子に作用する電磁力の大きさ $F_A=Bev$ [N] と遠心力 $F_B=\displaystyle\frac{m_o}{r}v^2$ とが釣り合った円運動であるので、その半径は $r=$( イ ) [m]と計算される。したがって、この円運動の周期は $T=$( ウ ) [s]、角周波数は $ω=$( エ ) [rad/s] となる。
ただし、電子の速さ $v$ [m/s] は、光速より十分小さいものとする。また、重力の影響は無視できるものとする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 裏からおもて | $\displaystyle\frac{m_ov}{eB^2}$ | $\displaystyle\frac{2πm_o}{eB}$ | $\displaystyle\frac{eB}{m_o}$ |
| (2) | おもてから裏 | $\displaystyle\frac{m_ov}{eB}$ | $\displaystyle\frac{2πm_o}{eB}$ | $\displaystyle\frac{eB}{m_o}$ |
| (3) | おもてから裏 | $\displaystyle\frac{m_ov}{eB}$ | $\displaystyle\frac{2πm_o}{e^2B}$ | $\displaystyle\frac{2e^2B}{m_o}$ |
| (4) | おもてから裏 | $\displaystyle\frac{2m_ov}{eB}$ | $\displaystyle\frac{2πm_o}{eB^2}$ | $\displaystyle\frac{eB^2}{m_o}$ |
| (5) | 裏からおもて | $\displaystyle\frac{m_ov}{2eB}$ | $\displaystyle\frac{πm_o}{eB}$ | $\displaystyle\frac{eB}{m_o}$ |
真空中において、磁束密度 $B$ [T] の一様な磁界が紙面と平行な平面の( おもてから裏 )へ垂直に加わっている。ここで、平面上の点 a に電荷 $-e$ [C]、質量 $m_o$ [kg] の電子をおき、図に示す向きに速さ $v$ [m/s] の初速度を与えると、電子は初速度の向き及び磁界の向きのいずれに対しても垂直で図に示す向きの電磁力 $F_A$ [N] を受ける。この力のために電子は加速度を受けるが速度の大きさは変わらないので、その方向のみが変化する。したがって、電子はこの平面上で時計回りに速さ $v$ [m/s] の円運動をする。この円の半径を $r$ [m] とすると、電子の運動は、磁界が電子に作用する電磁力の大きさ $F_A=Bev$ [N] と遠心力 $F_B=\displaystyle\frac{m_o}{r}v^2$ とが釣り合った円運動であるので、その半径は $r=$( $\displaystyle\frac{m_ov}{eB}$ ) [m]と計算される。したがって、この円運動の周期は $T=$( $\displaystyle\frac{2πm_o}{eB}$ ) [s]、角周波数は $ω=$( $\displaystyle\frac{eB}{m_o}$ ) [rad/s] となる。
答え (2)
2016年(平成28年)問12【電験理論の過去問題】
電荷 $q$ [C] をもつ荷電粒子が磁束密度 $B$ [T] の中を速度 $v$ [m/s] で運動するとき受ける電磁力はローレンツ力と呼ばれ、次のように導出できる。まず、荷電粒子を微小な長さ $Δl$ [m] をもつ線分とみなせると仮定すれば、単位長さ当たりの電荷(線電荷密度という。)は $\displaystyle\frac{q}{Δl}$ [C/m] となる。次に、この線分が長さ方向に速度 $v$ で動くとき、線分には電流 $\displaystyle\frac{vq}{Δl}$ [A] が流れていると考えられる。そして、この微小な線電流が受ける電磁力は $F=BIΔlsinθ$ [N] であるから、ローレンツ力の式 $F=$( ア ) [N] が得られる。ただし、$θ$ は $v$ と$B$ との方向がなす角である。$F$ は $v$ と $B$ の両方に直交し、$F$ の向きはフレミングの( イ )の法則に従う。では、真空中でローレンツ力を受ける電子の運動はどうなるだろうか。鉛直下向きの平等な磁束密度 $B$ が存在する空間に、負の電荷をもつ電子を速度 $v$ で水平方向に放つと、電子はその進行方向を前方とすれば( ウ )のローレンツ力を受けて( エ )をする。ただし、重力の影響は無視できるものとする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | $qvBsinθ$ | 右手 | 右方向 | 放物線運動 |
| (2) | $qvBsinθ$ | 左手 | 右方向 | 円運動 |
| (3) | $qvBΔlsinθ$ | 右手 | 左方向 | 放物線運動 |
| (4) | $qvBΔlsinθ$ | 左手 | 左方向 | 円運動 |
| (5) | $qvBΔlsinθ$ | 左手 | 右方向 | ブラウン運動 |
電荷 $q$ [C] をもつ荷電粒子が磁束密度 $B$ [T] の中を速度 $v$ [m/s] で運動するとき受ける電磁力はローレンツ力と呼ばれ、次のように導出できる。まず、荷電粒子を微小な長さ $Δl$ [m] をもつ線分とみなせると仮定すれば、単位長さ当たりの電荷(線電荷密度という。)は $\displaystyle\frac{q}{Δl}$ [C/m] となる。次に、この線分が長さ方向に速度 $v$ で動くとき、線分には電流 $\displaystyle\frac{vq}{Δl}$ [A] が流れていると考えられる。そして、この微小な線電流が受ける電磁力は $F=BIΔlsinθ$ [N] であるから、ローレンツ力の式 $F=$( $qvBsinθ$ ) [N] が得られる。ただし、$θ$ は $v$ と$B$ との方向がなす角である。$F$ は $v$ と $B$ の両方に直交し、$F$ の向きはフレミングの( 左手 )の法則に従う。では、真空中でローレンツ力を受ける電子の運動はどうなるだろうか。鉛直下向きの平等な磁束密度 $B$ が存在する空間に、負の電荷をもつ電子を速度 $v$ で水平方向に放つと、電子はその進行方向を前方とすれば( 右方向 )のローレンツ力を受けて( 円運動 )をする。ただし、重力の影響は無視できるものとする。
答え (2)
2018年(平成30年)問12【電験理論の過去問題】
次の文章は、磁界中の電子の運動に関する記述である。
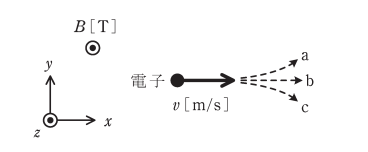
図のように、平等磁界の存在する真空かつ無重力の空間に、電子を x 方向に初速度 $v$ [m/s]で放出する。平等磁界は z 方向であり磁束密度の大きさ $B$ [T]をもつとし、電子の質量を $m$ [kg]、素電荷の大きさを $e$ [C]とする。ただし、紙面の裏側から表側への向きを z 方向の正とし、$v$ は光速に比べて十分小さいとする。このとき、電子の運動は( ア )となり、時間 $T=$ ( イ )[s]後に元の位置に戻ってくる。電子の放出直後の軌跡は破線矢印の( ウ )のようになる。
一方、電子を磁界と平行なz方向に放出すると、電子の運動は( エ )となる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
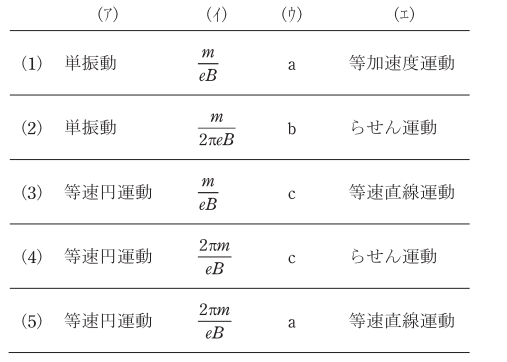
(ア)等速円運動
磁界に対して垂直に運動する電子にはローレンツ力が働き、等速円運動をします。
(イ)$T=\displaystyle\frac{2πm}{eB}$
磁界中の電子が一周するのにかかる時間 (周期) を求める式より $T=\displaystyle\frac{2πr}{v}=\displaystyle\frac{2πm}{qB}$
(ウ)a
電子は進行方向に対して左方向の力を受けます。したがって、電子放出後の軌跡は a になります。
(エ)等速直線運動
電子を磁界と平行な向きに放出すると、電子は磁界の影響を受けません。したがって、電子は等速直線運動を続けます。
答え(5)
電験三種の理論科目に出題される「電気電子工学(電気の現象)」のページ
1.電気の単位と抵抗温度係数
2.電界中の電子の運動
3.ローレンツ力の向きと円運動
4.電子放出と熱起電力の原理
5.過渡現象と時定数とは






