第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「トランジスタのバイアス回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「トランジスタのバイアス回路」の過去問題も解説しています。
バイアス回路
増幅回路を適切な動作状態にするために、回路にあらかじめ印加しておく直流電圧や電流のことを「バイアス」といいます。
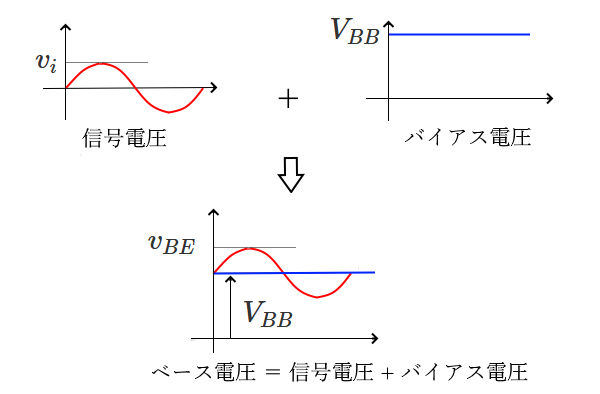
トランジスタのような電子部品は、ある程度の電圧がないと電流が流れず、回路が正しく動作しません。そこで、入力信号にバイアス電圧と呼ばれる一定の直流電圧を加えることで、信号全体の電圧レベルを底上げします。これにより、トランジスタが動作するために必要な最低限の電圧が確保され、回路が適切に機能するようになります。
バイアス回路の安定度
増幅回路の動作点は、バイアス回路によって決定されます。バイアス回路が不安定だと、動作点が変動し出力波形がひずみ、目的の出力を得ることができません。トランジスタは、温度変化による影響を受けやすい性質を持っています。そのため、温度変化により動作点が移動する特性があります。
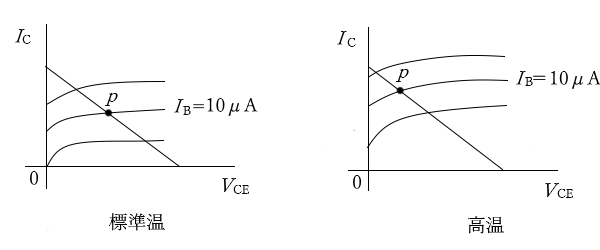
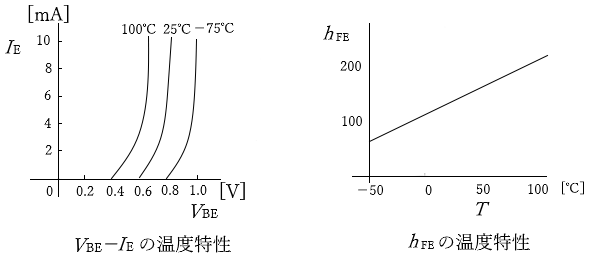
特にトランジスタのベースーエミッタ間電圧 $V_{BE}$ と直流電流増幅率 $h_{fe}$ は、温度変化により大きく変動します。ベースーエミッタ間電圧 $V_{BE}$ は、温度が上昇するにつれて減少し、直流電流増幅率 $h_{fe}$ は、温度が上昇するにつれて増加します。
温度上昇に伴って、流れる電流が増加すると、増加した電流の流れによってさらに温度は上昇します。これは、「熱暴走」といわれる現象で、最悪の場合はトランジスタを破壊してしまいます。そのため、増幅回路では、温度変化や直流電流増幅率 $h_{fe}$ のばらつきなどによる影響を受けにくい安定したバイアス回路を構成することが重要になります。
各種のバイアス回路
トランジスタは、ベースに一定の電圧を加えることで、初めて動作します。これを「ベースにバイアスをかける」ともいいます。トランジスタを正しく動作させるためには、適切なバイアス(バイアス電圧もしくは電流)を与え、そのバイアスを中心に信号(信号電圧もしくは電流)を与える必要があります。そのバイアスをかける方式の主なものとしては、「固定バイアス回路」「自己バイアス回路」「電流帰還バイアス回路」があります。
固定バイアス回路
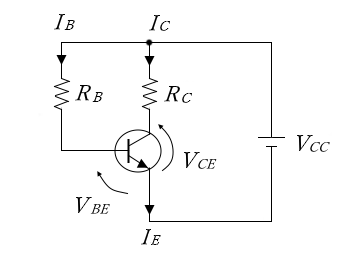
固定バイアス回路では、バイアス抵抗 $R_B$ によって電源 $V_{CC}$ からベース電流 $I_B$ を取り出します。$R_B$ の両端の電圧は、$V_{CC}-V_{BE}$ ですので、バイアス抵抗 $R_B$ は、次の式で求めることができます。
$R_B=\displaystyle\frac{V_{CC}-V_{BE}}{I_B}$ … (1)
また、$I_B$ と $I_C$ はそれぞれ次の式で表すことができます。
$I_B=\displaystyle\frac{V_{CC}-V_{BE}}{R_B}$ … (2)
$I_C=h_{fe}I_B=\displaystyle\frac{h_{fe}(V_{CC}-V_{BE})}{R_B}$ … (3)
ベース電圧 $V_{BE}$ の値は、Geトランジスタで 0.2V、Siトランジスタで 0.6V 程度ですので、
ベース電圧 $V_{BE}$ << 電源電圧 $V_{CC}$
とすれば、ベース電圧 $V_{BE}$ の変化によるベース電流 $I_B$ とコレクタ電流 $I_C$ の変動は、ほとんどないと考えることができます。
しかし、電流増幅率 $h_{fe}$ の増加に伴って、コレクタ電流 $I_C$ も比例して大きくなります。
次に、入力電源と出力端子を接続した図を示します。※1 のコンデンサは、「結合コンデンサ」といい、直流成分をカットして、交流成分だけを流すための役割があります。
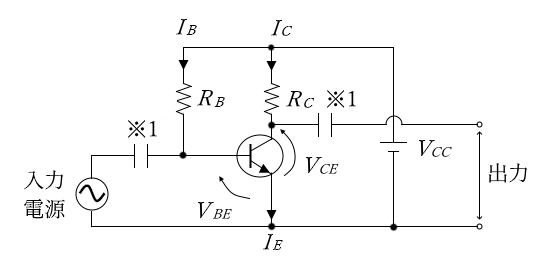
自己バイアス回路
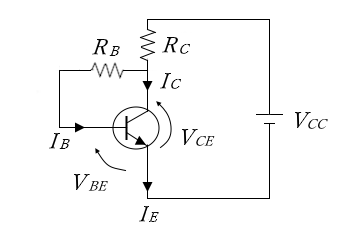
自己バイアス回路では、コレクタ端子からバイアス抵抗 $R_B$ によってベース電流 $I_B$ を取り出します。$R_B$ の両端の電圧は、$V_{CE}-V_{BE}$ ですので、バイアス抵抗 $R_B$ は、次の式で求めることができます。
$R_B=\displaystyle\frac{V_{CE}-V_{BE}}{I_B}$ … (4)
「ベース電流 $I_B$ << コレクタ電流 $I_C$ 」とすれば、
$V_{CE}=V_{CC}-(I_B+I_C)R_C$
$V_{CE}=V_{CC}-I_CR_C$ … (5)
式(5)を式(4)に代入し、整理します。
$I_B=\displaystyle\frac{V_{CE}-V_{BE}}{R_B}=\displaystyle\frac{V_{CC}-I_CR_C-V_{BE}}{R_B}$ … (6)
温度が上昇してコレクタ電流 $I_C$ が増加した場合、コレクタ電圧 $V_{CE}$ は現象します。すると、コレクタ電圧 $V_{CE}$ から供給していたベース電流 $I_B$ が減少し、コレクタ電流 $I_C$ も減少することになります($I_C=h{fe}I_B$)。
つまり、自己バイアス回路ではコレクタ電流 $I_C$ の増加を抑制するような働きがあります。このような働きを「負帰還」といいます。したがって、自己バイアス回路は安定度が良くなります。
安定度をより良くするには、$R_C$ を大きくすれば良いのですが、$R_C$ は負荷抵抗ですので最大値には限界があります。また、トランスなどのように内部抵抗が小さな負荷を接続する場合は、安定度の改善が出来ません。尚、自己バイアス回路は、電圧帰還バイアス回路と呼ばれることもあります。
次に、入力電源と出力端子を接続した図を示します。※1 のコンデンサは、結合コンデンサです。
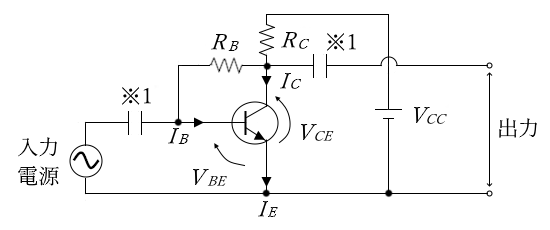
電流帰還バイアス回路
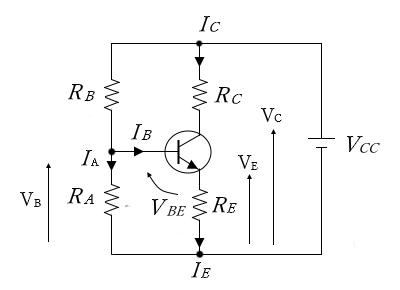
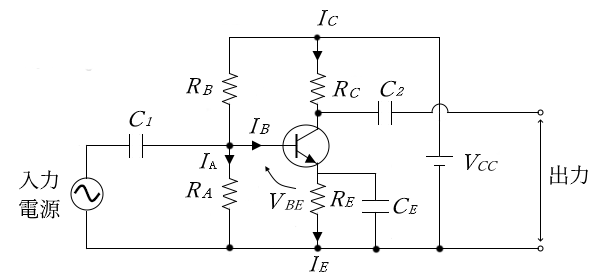
電流帰還バイアス回路では、抵抗 $R_A$ と $R_B$ によって電源電圧 $V_{CC}$ を分配しています。抵抗 $R_A$ と $R_B$ を「ブリーダ抵抗」、抵抗 $R_E$ を「安定抵抗」、電流 $I_A$ を「ブリーダ電流」といいます。この回路では、ブリーダ電流 $I_A$ をベース電流 $I_B$ よりも十分に大きな値(10~50倍程度)になるように設定します。すると、$V_{B}$ は一定値となります。
$V_{B}=\displaystyle\frac{R_A}{R_A+R_B}V_{CC}$ … (7)
温度が上昇してコレクタ電流 $I_C$ が増加した場合、抵抗 $R_E$ での電圧降下で $V_{E}$ が上昇し、ベース電圧 $V_{BE}$ は減少します。
$V_{E}=I_ER_E=(I_B+I_C)R_E$ … (8)
$V_{BE}=V_B-V_E$ … (9)
この回路ではベース電流 $I_B$ が減少して、コレクタ電流 $I_C$ を抑制することができます。安定抵抗 $R_E$ を大きくするほど安定度は良くなりますが、あまりにも大きくすると出力電圧が下がってしまいます。通常は $V_{E}$ が電源電圧 $V_{CC}$ の10~20%程度の値になるように安定抵抗 $R_E$ の値を決めています。
電流帰還回路は安定度が良いため、広く採用されていますが、ブリーダ電流を流すため消費電力が大きくなることが欠点です。
電流帰還バイアス回路を使って交流信号を増幅する場合には、入出力端子にコンデンサ $C_1$、$C_2$ を、安定抵抗 $R_E$ と並列にコンデンサ $C_E$ を挿入します。コンデンサ $C_1$、$C_2$ を結合コンデンサまたは、カップリングコンデンサと呼ばれ、入力と出力から直流信号を遮断し交流信号だけを取り出す働きをします。
また、コンデンサ $C_E$ は「バイパスコンデンサ」と呼ばれ、交流信号に対して $R_E$ をショートしてエミッタ接地回路を構成する働きがあります。
電験三種-理論の過去問解説:トランジスタのバイアス回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1999年(平成11年)問13【電験理論の過去問題】
図のトランジスタ増幅回路において、$V_{CC}=9$ [V]、$I_C=2$ [mA]であるとき、バイアス抵抗 $R_B$ [kΩ]の値として、正しいのは次のうちどれか。ただし、直流電流増幅率 $f_{fe}=100$、$V_{BE}=0.6$ [V]とする。
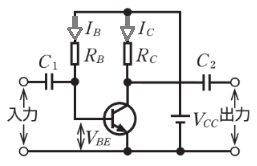
(1) 360 (2) 420 (3) 510 (4) 630 (5) 740
固定バイアス回路の問題です。$h{fe}=\displaystyle\frac{I_C}{I_B}$ ですので、
$100=\displaystyle\frac{2×10^{-3}}{I_B}$
$I_B=2×10^{-5}$
$R_B$ の両端の電圧は、$V_{CC}-V_{BE}$ です。バイアス抵抗 $R_B$ は、
$R_B=\displaystyle\frac{V_{CC}-V_{BE}}{I_B}=\displaystyle\frac{9-0.6}{2×10^{-5}}=420$ [kΩ]
答え (2)
2002年(平成14年)問13【電験理論の過去問題】
図1、図2及び図3は、トランジスタ増幅器のバイアス回路を示す。次の(a)及び(b)に答えよ。
ただし、$V_{CC}$ は電源電圧、$V_B$ はベース電圧,$I_B$ はベース電流,$I_C$ はコレクタ電流,$I_E$ はエミッタ電流、$R$,$R_B$,$R_C$ 及び $R_E$ は抵抗を示す。
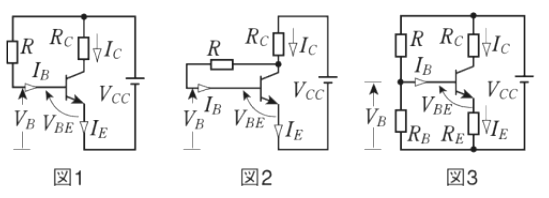
(a) 次の式①,式②及び式③は、図1,図2及び図3のいずれかの回路のベース・エミッタ間の電圧 $V_{BE}$ 示す。
$V_{BE}=V_B-I_E・R_E$ … ①
$V_{BE}=V_{CC}-I_B・R$ … ②
$V_{BE}=V_{CC}-I_B・R-I_C・R_C$ … ③
上記の式と図を正しく組み合わせたものは次のうちどれか。
| 式① | 式② | 式③ | |
| (1) | 図1 | 図2 | 図3 |
| (2) | 図2 | 図3 | 図1 |
| (3) | 図3 | 図1 | 図2 |
| (4) | 図1 | 図3 | 図2 |
| (5) | 図3 | 図2 | 図1 |
(b) 次の文章1,2及び3は、それぞれのバイアス回路における周囲温度の変化とその増幅特性の関係について述べたものである。
- 温度上昇により $I_B$ が増加すると、増幅特性が安定しないバイアス回路の図は( ア )である。
- 温度上昇により $I_B$ が増加すると、$I_E$ も増加する。他方、$V_B$ は一定であるから $V_{BE}$ が減少するので、増幅特性が最も安定するバイアス回路は図の( イ )である。
- ( ウ )のバイアス回路は、温度上昇により $I_B$ が増加すると、$R_C$ の電圧降下でコレクタ・エミッタ間の電圧 $V_{CE}$ が抑えられ、増幅特性が安定する。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 図1 | 図2 | 図3 |
| (2) | 図2 | 図3 | 図1 |
| (3) | 図3 | 図1 | 図2 |
| (4) | 図1 | 図3 | 図2 |
| (5) | 図2 | 図1 | 図3 |
(a) それぞれの回路の電圧を表します。
図1:$V_{CC}=RI_B+{V_BE}$ … 式②
図2:$V_{CC}=R_CI_C+RI_B+V_{BE}$ … 式③
図3:$V_{B}=V_{BE}+R_EI_E$ … 式①
答え (3)
(b) 図1は固定バイアス回路、図2は自己バイアス回路、図3は電流帰還バイアス回路です。
- 温度上昇により $I_B$ が増加すると、増幅特性が安定しないバイアス回路の図は( 図1 )である。
- 温度上昇により $I_B$ が増加すると、$I_E$ も増加する。他方、$V_B$ は一定であるから $V_{BE}$ が減少するので、増幅特性が最も安定するバイアス回路は図の( 図3 )である。
- ( 図2 )のバイアス回路は、温度上昇により $I_B$ が増加すると、$R_C$ の電圧降下でコレクタ・エミッタ間の電圧 $V_{CE}$ が抑えられ、増幅特性が安定する。
答え (4)
2017年(平成29年)問13【電験理論の過去問題】
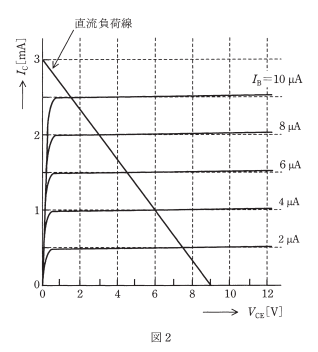
図1は、固定バイアス回路を用いたエミッタ接地トランジスタ増幅回路である。図2は、トランジスタの五つのベース電流 $I_B$ に対するコレクターエミッタ間電圧 $V_{CE}$ とコレクタ電流 $I_C$ との静特性を示している。この $V_{CE}-I_C$ 特性と直流負荷線との交点を動作点という。図1の回路の直流負荷線は図2のように与えられる。動作点が $V_{CE}= 4.5V$ のとき、バイアス抵抗 $R_B$ の値[MΩ]として最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ベース-エミッタ間電圧 $V_{BE}$ は直流電源電圧 $V_{CC}$ に比べて十分小さく無視できるものとする。なお、$R_L$ は負荷抵抗であり、$C_1$,$C_2$ は結合コンデンサである。
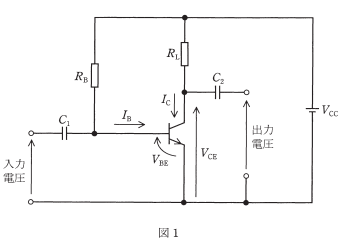
(1) 0.5 (2) 1.0 (3) 1.5 (4) 3.0 (5) 6.0
2017年(平成29年)問13 過去問解説
バイアス抵抗 $R_B$ の端子間電圧を $V_{RB}$[V]、負荷抵抗 $R_L$ の端子間電圧を $V_{RL}$[V]とし、バイアス回路のみについて考えます。
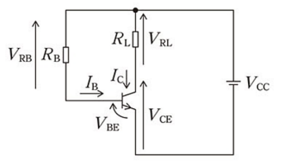
バイアス抵抗 $R_B$ は、
$R_B=\displaystyle\frac{V_{RB}}{I_B}$
キルヒホッフの法則より
$V_{CC}=V_{RB}+V_{BE}$
$V_{CC}=V_{RL}+V_{CE}=R_LI_C+V{CE}$
ベース-エミッタ間電圧 $V_{BE}$ は直流電源電圧 $V_{CC}$ に比べて十分小さく無視できるものとするとありますので、$V_{BE}=0$ として考えると、
$V_{CC}=V_{RB}$
$R_B=\displaystyle\frac{V_{CC}}{I_B}$
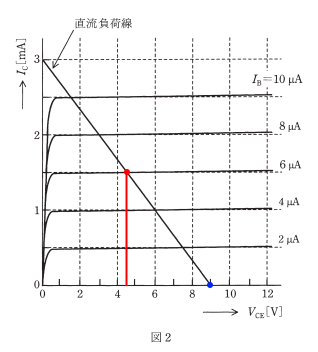
図2より、$I_C=0$ のとき、$V_{CC}=9$[V]ですので、式 $V_{CC}=R_LI_C+V{CE}$ に代入すると、
$V_{CC}=R_LI_C+V{CE}=R_L×0+9=9$[V]
動作点が $V_{CE}= 4.5V$ のとき、ベース電流 $I_B=6$[μA]ですので、
$R_B=\displaystyle\frac{V_{RB}}{I_B}=\displaystyle\frac{9}{6×10^{-6}}=1.5×10^6=1.5$[MΩ]
答え(3)
電験三種の理論科目に出題される「電子回路」のページ
1.p型半導体とn型半導体
2.ダイオードとトランジスタの特性
3.トランジスタ増幅回路
4.トランジスタのバイアス回路
5.トランジスタの等価回路
6.FET増幅回路
7.多段・負帰還・電力増幅回路
8.オペアンプ(反転・非反転増幅回路)
9.発振回路と変調回路の原理
10.波形整形回路(クリッパ回路とリミッタ回路)






