第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「トランジスタの等価回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「トランジスタの等価回路」の過去問題も解説しています。
等価回路の考え方
バイアスを与えたトランジスタ増幅回路に、信号を加えると増幅します。例えばバイアスは直流で、信号は小信号の交流を考えます。この回路では、増幅回路には直流分と交流分が重なって出力されます。トランジスタは電圧と電流の特性が正比例しない非線形のデバイスですが、小信号を考えた場合では、特性曲線を直線とみなした線形デバイスと考えることができます。したがって、交流分を扱った増幅回路では、電気的に等しい等価回路に置き換えることで、回路の解析ができるようになります。
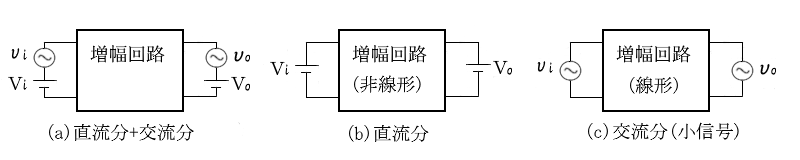
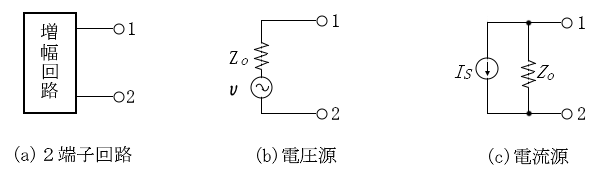
増幅回路を入力側または出力側から見た場合、テブナンの定理を適用することができます。また、ショートした場合に流れる電流を $I_S$ とすると、ノートンの定理を適用することができます。次の図で、$v$ は端子をオープンにした場合の電圧、$Z_o$ は回路内の電源をショートした場合の内部インピーダンスを表します。
hパラメータの等価回路
トランジスタ増幅回路では回路計算を簡単にするために、トランジスタ増幅回路を「簡易等価回路」に置き換えて、「hパラメータ」を使う方法があります。hパラメータとは、各入出力の電圧や電流を用いて 増幅回路の性能を表すための数値です。
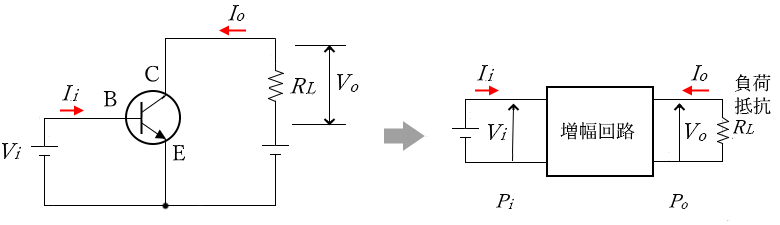
図のような、エミッタ接地増幅回路のhパラメータには、入力インピーダンス($h_{ie}$)、電圧帰還率($h_{re}$)、電流増幅率($h_{fe}$)、出力アドミタンス($h_{oe}$)の4種類があります。
入力インピーダンス:$h_{ie}=\displaystyle\frac{V_i}{I_i}$ [Ω]
電圧帰還率:$h_{re}=\displaystyle\frac{V_i}{V_o}$
電流増幅率:$h_{fe}=\displaystyle\frac{I_o}{I_i}$
出力アドミタンス:$h_{oe}=\displaystyle\frac{I_o}{V_o}$ [S]
また、電圧増幅率とは入力電圧に対する出力電圧の割合を表したものです。電圧増幅率が大きければ、少ない入力電圧で大きな出力電圧を得られることを意味します。
$電圧増幅率=\displaystyle\frac{出力電圧}{入力電圧}=\displaystyle\frac{V_o}{V_i}$
簡易等価回路
エミッタ接地増幅回路を、簡易等価回路に変換した図は、次のようになります。
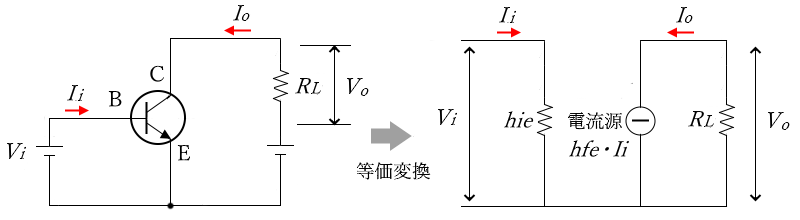
等価回路中の $h_{ie}$ は、入力側のインピーダンスを表しています。入力側回路に、オームの法則を適用すると
$h_{ie}=\displaystyle\frac{V_i}{I_i}$
の関係式を導き出すことができます。
また、等価回路中の $h_{fe}h$ は、電流増幅率のことで、$h_{fe}=\displaystyle\frac{I_o}{I_i}$ の関係式があります。この式を変形すると、
$I_o=h_{fe}・{I_i}$
電流帰還バイアス回路の等価回路
次の図は、電流帰還バイアス回路を示します。
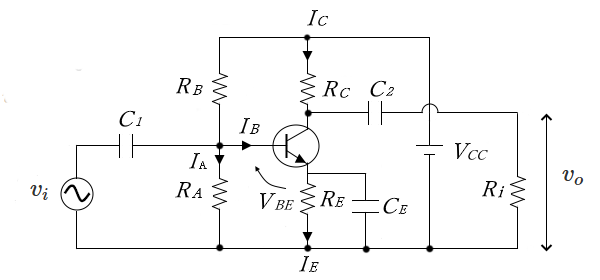
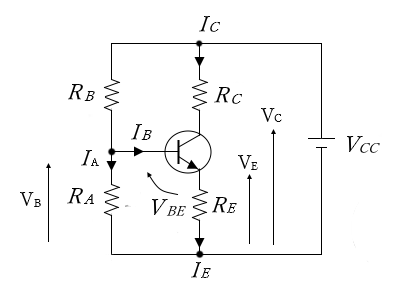
$R_i$ は負荷抵抗を示していますが、多段増幅回路においては、次段の入力インピーダンスと考えることができます。直流分においては、各コンデンサはオープンの状態となりますので、次の図のような等価回路になります。
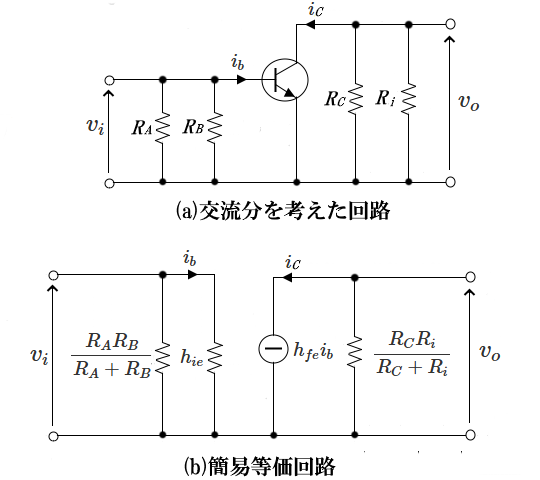
交流分においては、結合コンデンサ $C_1$、$C_2$、バイパスコンデンサ $C_E$ のインピーダンスは、周波数によりますが、インピーダンスがかなり小さいので、ショートと考えることができます。交流分のみ扱いますので、直流電源 $V_{CC}$ をショートして考えますと、次の図(a)のような回路が得られます。これより図(a)より、図(b)のような簡易化したhパラメータ交流等価回路が得られます。簡易等価回路では、入力抵抗 $R_A$ と $R_B$ および出力側の負荷抵抗は、合成抵抗になります。
電験三種-理論の過去問解説:トランジスタの等価回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2001年(平成13年)問13
図のようなトランジスタ増幅器の交流に注目した回路において、交流の入力信号電圧 $v_i=12$ [mV] を加えたところ、ベース入力信号電流 $i_b=5$ [μA] が流れた。この場合の(a)及び(b)に答えよ。
ただし、トランジスタの小信号電流増幅率 $h_{fe}=120$ 、抵抗 $R_c=2$ [kΩ] とする。
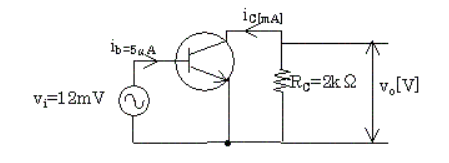
(a) コレクタに流れる出力信号 $i_c$ [mA] の値として、正しいのは次のうちどれか。
(1) 0.2 (2) 0.3 (3) 0.4 (4) 0.5 (5) 0.6
(b) 抵抗 $R_c$ の両端の信号電圧 $v_o$ [V] を出力したとき、電圧増幅度の値として正しいのは次のうちどれか。
(1) 100 (2) 110 (3) 120 (4) 150 (5) 180
(a) $h_{fe}=\displaystyle\frac{i_c}{i_b}$
$ i_c=h_{fe}×i_b=120×5×10^{-6}=0.6×10^{-3}=0.6 [mA] $
答え (5)
(b) $v_o=i_c× R_c=0.6×10^{-3}×2×10^{3}=1.2$ [V]
$A_v=\left|\displaystyle\frac{v_o}{v_i}\right|=\left|\displaystyle\frac{1.2}{12×10^{-3}}\right|=100$
答え (1)
2005年(平成17年)問12
図は、エミッタを接地したトランジスタ電圧増幅器の簡易小信号等価回路である。この回路において、電圧増幅度が120となるとき、負荷抵抗 $R_L$ [kΩ] の値として、最も近いのは次のうちどれか。
ただし、$v_i$ を入力電圧、$v_o$ を出力電圧とし、トランジスタの電流増幅率 $h_{fe}=140$、入力インピーダンス $h_{ie}=2.30$ [kΩ] とする。
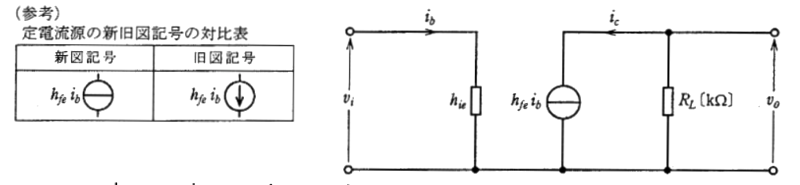
(1) 0.37 (2) 1.97 (3) 2.68 (4) 5.07 (5) 7.30
題意より
$v_i=h_{ie}i_b$
$i_c=h_{fe}i_b$
$v_o=R_Li_c$
電圧増幅度を $A_v$ とすると、
$A_v=\left|\displaystyle\frac{v_o}{v_i}\right|=\left|\displaystyle\frac{R_Li_c}{h_{ie}i_b}\right|=\left|\displaystyle\frac{R_Lh_{fe}i_b}{h_{ie}i_b}\right|=\left|\displaystyle\frac{R_Lh_{fe}}{h_{ie}}\right|$
$120=\left|\displaystyle\frac{R_L×140}{2.30×10^3}\right|$
$R_L=\displaystyle\frac{120×2.30×10^3}{140}≒1.97×10^3=1.97$ [kΩ]
答え (2)
2006年(平成18年)問18
図1のようなトランジスタ増幅回路がある。次の(a)及び(b)に答よ。
ただし、RA,RB,RC,RE,RLは抵抗、C1,C2,C3はコンデンサ、VDDは直流電圧源、vi,voは交流信号電圧とする。
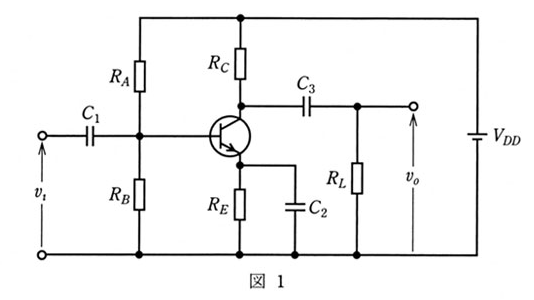
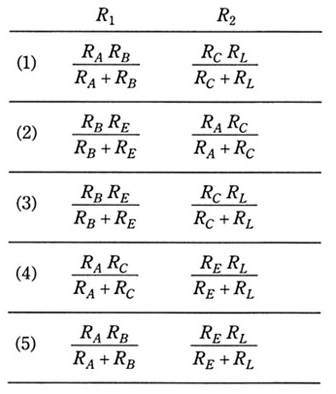
(a) 図1の回路を交流信号に注目し、交流回路として考える。この場合、この回路を図2のような等価な回路に置き換えることができる。このとき等価な抵抗 R1,R2 の値を表す式として、正しいのは次のうちどれか。
ただし、C1,C2,C3 のインピーダンスは十分小さく無視できるものとする。
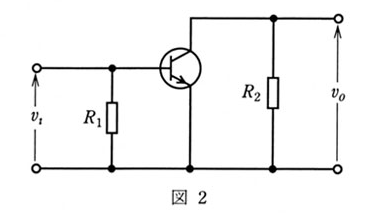
(b) 図2の回路で、トランジスタの入力インピーダンス hie=6 [kΩ]、電流増幅率 hfe=140 であった。この回路の電圧増幅度の大きさとして、最も近いのは次のうちどれか。
ただし、図1の回路において、各抵抗は RA=100 [kΩ],RB=25 [kΩ],RC=8 [kΩ],RE=2.2 [kΩ],RL=15 [kΩ]とし、出力アドミタンス hoe 及び電圧帰還率 hre は無視できるものとする。
(1) 15.7 (2) 82 (3) 122 (4) 447 (5) 753
(a) C1,C2,C3 のインピーダンスは十分小さく無視できるとありますので、ショートと考えます。図2の入力抵抗 $R_1$ は $R_A$ と $R_B$ の合成抵抗、出力抵抗 $R_2$ は $R_C$ と $R_L$ の合成抵抗になりますので、
$R_1=\displaystyle\frac{R_AR_B}{R_A+R_B}$
$R_2=\displaystyle\frac{R_CR_L}{R_C+R_L}$
答え (1)
(b) 電圧増幅度 $A_v$ は、
$A_v=\displaystyle\frac{v_o}{v_i}=\displaystyle\frac{h_{fe}i_bR_2}{i_bh_{ie}}=\displaystyle\frac{140×\frac{120}{23}×10^3}{6×10^3}=122$
答え (3)
2009年(平成21年)問18
図1の回路は、エミッタ接地のトランジスタ増幅器の交流小信号に注目した回路である。次の(a)及び(b)に答えよ。
ただし、RL [Ω] は抵抗、$i_b$ [A] は入力信号電流、$i_c=6×10^(-3)$ [A] は出力信号電流、$v_b$ [V] は入力信号電圧、$v_c=6$ [V] は出力信号電圧である。
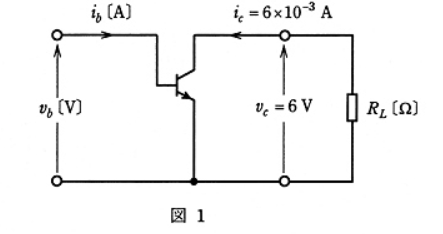
(a) 図1の回路において、入出力信号の関係を表1に示すhパラメータを用いて表すと次の式①、②になる。
$v_b=h_{ie} i_b+h_re v_c$ ・・・ ①
$i_c=h_{fe} i_b+h_{oe} v_c$ ・・・ ②
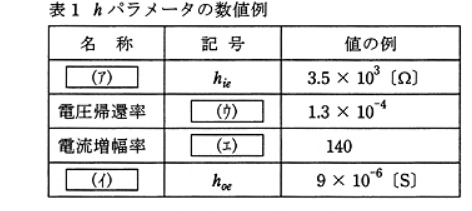
上記表中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたものは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 入力インピーダンス | 出力アドミタンス | $h_{fe}$ | $h_{re}$ |
| (2) | 入力コンダクタンス | 出力インピーダンス | $h_{fe}$ | $h_{re}$ |
| (3) | 出力コンダクタンス | 入力インピーダンス | $h_{re}$ | $h_{fe}$ |
| (4) | 出力コンダクタンス | 入力コンダクタンス | $h_{re}$ | $h_{fe}$ |
| (5) | 入力インピーダンス | 出力アドミタンス | $h_{re}$ | $h_{fe}$ |
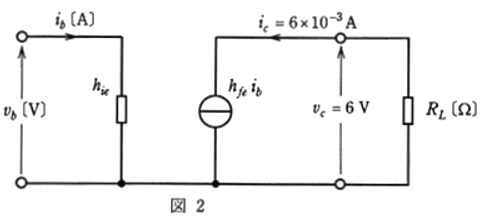
(b) 図1の回路の計算は、図2の簡易小信号等価回路を用いて行うことが多い。この場合、上記(a)の式①、②から求めた $v_b$ [V] 及び $i_b$ [A] の値をそれぞれ真の値としたとき、図2の回路から求めた $v_b$ [V]及び $i_b$ [A]の誤差 $Δv_b$ [mV]、$Δi_b$ [μA] の大きさとして、最も近いものを組み合わせたのは次のうちどれか。
ただし、hパラメータの値はは表1に示された値とする。
Δvb Δib
(1) 0.78 54
(2) 0.78 6.5
(3) 0.57 6.5
(4) 0.57 0.39
(5) 0.35 0.39
(a) hパラメータはトランジスタの四定数といわれるものです。
$h_{ie}$:入力インピーダンス
$h_{re}$:電圧帰還率
$h_{fe}$:電流増幅率
$h_{oe}$:出力アドミタンス
答え (5)
(b) hパラメーターの関係式は、
$v_{b}=h_{ie}i_b+h_{re}v_{c}$
$i_c=h_{fe}i_b+h_{oe}v_{c}$
ですので、
$i_c=h_{fe}i_b+h_{oe}v_{c}$
$6×10^{-3}=140i_b+9×10^{-6}×6$
$i_b=4.24714×10^{-5}$[A]
$\begin{eqnarray}v_{b}&=&h_{ie}i_b+h_{re}v_{c}\\\\&=&3.5×10^3×4.24714×10^{-5}+1.3×10^{-4}×6\\\\&=&0.14943[V]\end{eqnarray}$
簡易小信号等価回路では、 $h_{re}$ と $h_{oe}$ は、非常に小さな値ですので、これらを 0 とみなすことができます。したがって、図2の回路のhパラメーターの関係式は、
$v’_{b}=h_{ie}i’_b$
$i’_c=h_{fe}i’_b$
となりますので、
$i’_c=h_{fe}i’_b$
$6×10^{-3}=140i’_b$
$i’_b=4.28571×10^{-5}$[A]
$v’_{b}=h_{ie}i’_b=3.5×10^3×4.28571×10^{-5}=0.15$[V]
したがって $Δv_b$ [mV]、$Δi_b$ [μA]の大きは、
$Δv_b=v’_{b}-v_{b}=0.15-0.14943=0.57$ [mV]
$\begin{eqnarray}Δi_b&=&i’_b-i_b\\\\&=&4.28571×10^{-5}-4.24714×10^{-5}\\\\&=&0.39 [μA]\end{eqnarray}$
答え (4)
2011年(平成23年)問18
図 1 のトランジスタによる小信号増幅回路について、次の(a)及び(b)の問に答えよ。
ただし、各抵抗は、 $R_A=100$ [kΩ] ,$R_B=600$ [kΩ],$R_C=5$ [kΩ],$R_D=1$ [kΩ],$R_o=200$ [kΩ] である。 $C_1$ ,$C_2$ は結合コンデンサで、$C_3$ はバイパスコンデンサである。また、$V_{CC}=12$ [V] は直流電源電圧、$V_{be}=0.6$ [V] はベースーエミッタ間の直流電圧とし、$v_i$ [V] は入力小信号電圧、$v_o$ [V] は出力小信号電圧とする。
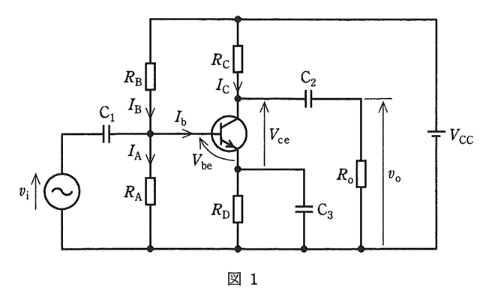
(a) 小信号増幅回路の直流ベース電流 $I_b$ [A] が抵抗 $R_A$、$R_C$ の直流電流 $I_A$ [A] や $I_C$ [A] に比べて十分に小さいものとしたとき、コレクターエミッタ間の直流電圧 $V_{ce}$ [V] の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.1 (2) 1.7 (3) 4.5 (4) 5.3 (5) 6.4
(b) 小信号増幅回路の交流等価回路は、結合コンデンサ及びバイパスコンデンサのインピーダンスを無視することができる周波数において、一般に、図2の簡易等価回路で表される。
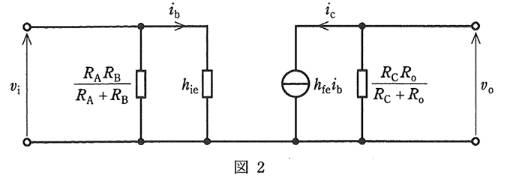
ここで、$i_b$ [A]はベースの信号電流、$i_c$ [A]はコレクタの信号電流で、この回路の電圧増幅度 $A_{vo}$ は下式となる。
$A_{vo}=\left|\displaystyle\frac{v_o}{v_i}\right|=\displaystyle\frac{h_{fe}}{h_{ie}}・\displaystyle\frac{R_CR_o}{R_C+R_o}$ … ①
また、コンデンサ $C_1$ のインピーダンスの影響を考慮するための等価回路を図3に示す。
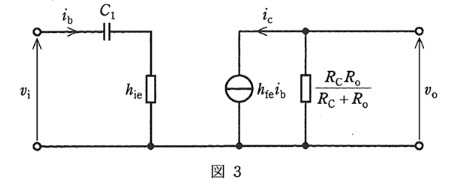
このとき、入力小信号電圧のある周波数において、図3を用いて得られた電圧増幅度が①式で示す電圧増幅度の $\displaystyle\frac{1}{\sqrt{2}}$ となった。この周波数[Hz]の大きさとして、最も近いものを次の(1)~(5)のうちから一つ選べ
ただし、エミッタ接地の小信号電流増幅率 $h_{fe}=120$、入力インピーダンス $h_{ie}=3×10^3$ [Ω]、コンデンサ $C1$ の静電容量 $C_1=10$ [μF] とする。
(1) 1.2 (2) 1.6 (3) 2.1 (4) 5.3 (5) 7.9
(a) 図は、電流帰還バイアス回路です。ベース電圧を $V_{B}$ とすると、
$\begin{eqnarray}V_{B}&=&\displaystyle\frac{R_A}{R_A+R_B}V_{CC}\\\\&=&\displaystyle\frac{100[kΩ]}{100[kΩ]+600[kΩ]}×12\\\\&=&1.714 [V] \end{eqnarray}$
抵抗 $R_D$ の端子電圧を $V_{RD}$ [V]とすると、
$V_{RD}=V_B-V_{be}=1.714-0.6=1.114$ [V]
エミッタ電流は $I_C$ [A]と等しくなりますので、抵抗 $R_C$ の端子電圧を $V_{RC}$ [V]とすると、$V_{RD}$ の5倍($R_C/R_D=5$)になります。
$V_{RC}=5V_{RD}=5.570$ [V]
$V_{RC}+V_{ce}+V_{RD}=V_{CC}$ ですので、
$\begin{eqnarray}V_{ce}&=&V_{CC}-V_{RC}-V_{RD}\\&=&12-5.570-1.114\\&=&5.316 [V] \end{eqnarray}$
答え (4)
(b) 図3の入力側の合成インピーダンスを $Z$、出力側の合成抵抗を $R_L$ 、電圧増幅度を $A’_{vo}$ とすると
$Z=\sqrt{(h_{ie})^2+\left(\displaystyle\frac{1}{ωC_1}\right)^2}$
$R_L=\displaystyle\frac{R_CR_o}{R_C+R_o}$
$i_b=\displaystyle\frac{v_i}{Z}$
$i_c=h_{fe}i_c=\displaystyle\frac{h_{fe}v_i}{Z}$
$v_o=-i_cR_L=-\displaystyle\frac{h_{fe}v_iR_L}{Z}$
$A’_{vo}=\left|\displaystyle\frac{v_o}{v_i}\right|=\displaystyle\frac{h_{fe}R_L}{Z}$
図3を用いて得られた電圧増幅度が①式で示す電圧増幅度の $\displaystyle\frac{1}{\sqrt{2}}$ となりますので、
$A’_{vo}=\displaystyle\frac{A_{vo}}{\sqrt{2}}$
$\displaystyle\frac{h_{fe}R_L}{Z}=\displaystyle\frac{1}{\sqrt{2}}×\displaystyle\frac{h_{fe}}{h_{ie}}・R_L$
$Z=\sqrt{2}h_{ie}$
$\sqrt{(h_{ie})^2+\left(\displaystyle\frac{1}{ωC_1}\right)^2}=\sqrt{2}h_{ie}$
上式を整理すると、
$ωC_1=\displaystyle\frac{1}{h_{ie}}$
$2πfC_1=\displaystyle\frac{1}{h_{ie}}$
$f=\displaystyle\frac{1}{2π×10×10×10^{-6}×3×10^3}=5.305$
答え (4)
2016年(平成28年)問13
図は、エミッタ(E)を接地したトランジスタ増幅回路の簡易小信号等価回路である。この回路においてコレクタ抵抗 RC と負荷抵抗 RL の合成抵抗が RL‘=1kΩ のとき、電圧利得は 40dB であった。入力電圧 vi=10mV を加えたときにベース(B)に流れる入力電流 ib の値 [μA] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、vo は合成抵抗 RL‘ の両端における出力電圧、iC はコレクタ(C)に流れる出力電流、hie はトランジスタの入力インピーダンスであり、小信号電流増幅率 hfe=100 とする。
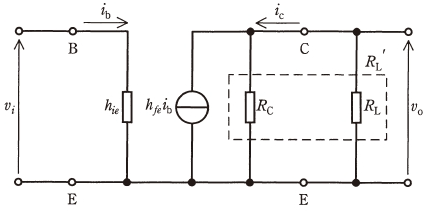
(1) 0.1 (2) 1 (3) 10 (4) 100 (5) 1000
電圧利得 $G_v$ は40 [dB] ですので、
$G_v=20log_{10}A_v=20log_{10}\left|\displaystyle\frac{v_o}{v_i}\right|=40$ [dB]
$log_{10}\left|\displaystyle\frac{v_o}{v_i}\right|=2$
$\left|\displaystyle\frac{v_o}{v_i}\right|=10^2$ … (1)
等価回路のhパラメーターの関係式は、
$v_{i}=h_{ie}i_b$
$v_o=-R’_Lh_{fe}i_b$
したがって、
$v_o=-R’_Lh_{fe}×\displaystyle\frac{v_{i}}{h_{ie}}$
$\left|\displaystyle\frac{v_o}{v_{i}}\right|=\displaystyle\frac{R’_Lh_{fe}}{h_{ie}}=\displaystyle\frac{1000×100}{h_{ie}}$ … (1)
式(1)と(2)より、$h_{ie}=1000$ となります。
したがって、$v_i=10$ [mV]のときの $i_b$ [A]は、
$v_{i}=h_{ie}i_b$
$10×10^{-3}=1000i_b$
$i_b=10$ [μA]
答え (3)
2018年(平成30年)問16【電験理論の過去問題】
エミッタホロワ回路について、次の(a)及び(b)の問に答えよ。
(a) 図1の回路で VCC=10V、R1=18kΩ、R2=82kΩ とする。動作点におけるエミッタ電流を 1mA としたい。抵抗 RE の値[kΩ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、動作点において、ベース電流は R2 を流れる直流電流より十分小さく無視できるものとし、ベース-エミッタ間電圧は 0.7V とする。
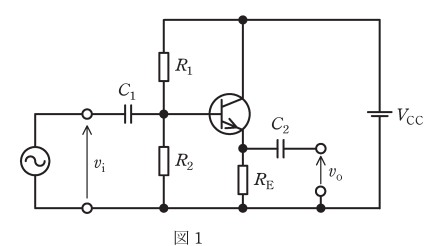
(1) 1.3 (2) 3.0 (3) 7.5 (4) 13 (5) 75
(b) 図2は、エミッタホロワ回路の交流等価回路である。ただし、使用する周波数において図1の二つのコンデンサのインピーダンスが十分に小さい場合を考えている。ここで、hie=2.5kΩ、hfe=100であり、RE は小問(a)で求めた値とする。入力インピーダンス $\displaystyle\frac{v_i}{i_i}$ の値 [kΩ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、vi と ii はそれぞれ図2に示す入力電圧と入力電流である。
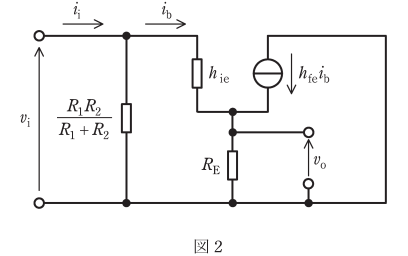
(1) 2.5 (2) 15 (3) 80 (4) 300 (5) 750
(a) R2 にかかる電圧を V2 とします。VCC ,R1 ,R2 を抜き出した回路は次のようになります。

電圧 V2 を求めます。
$V_2=\displaystyle\frac{82}{18+82}×10=8.2$[V]
トランジスタ と RE ,R2 を抜き出した回路図を示します。
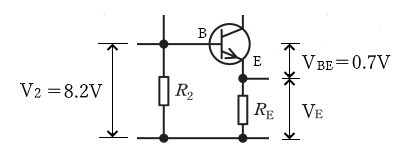
$R_E$ にかかる電圧を $V_E$ とすると、
$V_E=V_2-V_{BE}=8.2-0.7=7.5$[V]
エミッタ電流が 1mA となる $R_E$ の値は、
$R_E=\displaystyle\frac{V_E}{I_E}=\displaystyle\frac{7.5}{1×10^{-3}}=7.5×10^3$[Ω]
答え (a)-(3)
(b) $R_1=18kΩ、R_2=82kΩ$ ですので、
$\displaystyle\frac{R_1R_2}{R_1+R_2}=\displaystyle\frac{18×82}{18+82}=14.76$[kΩ]
各抵抗の電圧降下は、次のとおりです。
$\displaystyle\frac{R_1R_2}{R_1+R_2}$ の電圧降下:$14.76k(i_1-i_b)$
$h_{ie}$ の電圧降下:$2.5ki_b$
$R_E$ の電圧降下:$7.5k(i_b+h_{fe}i_b)=7.5k(i_b+100i_b)$
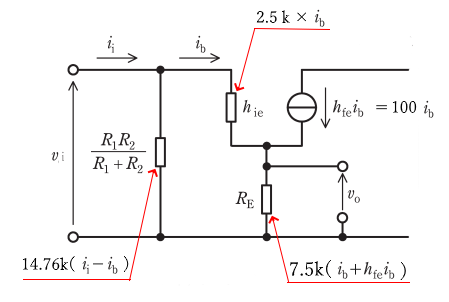
並列回路の電圧は等しいので、次の式が成り立ちます。
$v_i=14.76k(i_1-i_b)=2.5ki_b+7.5k(101i_b)$
この式を解いて、$i_b$ を求めます。
$14.76k(i_1-i_b)=2.5ki_b+7.5k(101i_b)$
$14.76ki_1=2.5ki_b+757.5ki_b+14.76ki_b$
$14.76ki_1=774.76ki_b$
$i_b=\displaystyle\frac{14.76}{774.76}i_1$
$v_i=14.76k(i_1-i_b) $ に $i_b=\displaystyle\frac{14.76}{774.76}i_1$ を代入します。
$v_i=14.76k(i_1-\displaystyle\frac{14.76}{774.76}i_1)$
$v_i=14.48ki_1$
$\displaystyle\frac{v_1}{i_1}=14.48k≒15k$
答え (b)-(2)
電験三種の理論科目に出題される「電子回路」のページ
1.p型半導体とn型半導体
2.ダイオードとトランジスタの特性
3.トランジスタ増幅回路
4.トランジスタのバイアス回路
5.トランジスタの等価回路
6.FET増幅回路
7.多段・負帰還・電力増幅回路
8.オペアンプ(反転・非反転増幅回路)
9.発振回路と変調回路の原理
10.波形整形回路(クリッパ回路とリミッタ回路)






