電験3種の法規で出題される電線路の計算問題の過去問を、解説しています。難関問題が多く、たいへん苦労すると思いますが、電力科目と理論科目をきっちりと理解していれば、新たに覚えるところはありません。まずは、解きかたのパターンを覚えて、対応できるようにしましょう。
- 電験3種-法規(施設管理)過去問題
- 1997年(平成9年)問11
- 1997年(平成9年)問11 過去問解説
- 2003年(平成15年)問12
- 2003年(平成15年)問12 過去問解説
- 2005年(平成17年)問12
- 2005年(平成17年)問12 過去問解説
- 2006年(平成18年)問13
- 2006年(平成18年)問13 過去問解説
- 2009年(平成21年)問11
- 2009年(平成21年)問11 過去問解説
- 2009年(平成21年)問13
- 2009年(平成21年)問13 過去問解説
- 2010年(平成22年)問11
- 2010年(平成22年)問11 過去問解説
- 2011年(平成23年)問13
- 2011年(平成23年)問13 過去問解説
- 2013年(平成25年)問11
- 2013年(平成25年)問11 過去問解説
- 2014年(平成26年)問13
- 2014年(平成26年)問13 過去問解説
- 2016年(平成28年)問13
- 2016年(平成28年)問13 過去問解説
- 2017年(平成29年)問12
- 2017年(平成29年)問12 過去問解説
電験3種-法規(施設管理)過去問題
1997年(平成9年)問11
定格容量 100[kVA]、一次電圧 6600[V]、二次電圧 210[V]の単相変圧器に単相2線式1回線の低圧架空電線路が接続されている。この低圧電線路中絶縁部分の電線と大地との間の絶縁抵抗を保つために、維持しなければならない漏えい電流の最大値は1線当たり何アンペアか。適切な値を次のうちから選べ。
(1) 0.095 (2) 0.119 (3) 0.158 (4) 0.238 (5) 0.476
1997年(平成9年)問11 過去問解説
変圧器の最大供給電流を $I_m$[A]とすると、
$I_m=\displaystyle \frac{ 100×10^3 }{ 210 }=476$[A]
したがって、1線当たりの許容最大漏えい電流 $I_l$[A]は、
$I_l=\displaystyle \frac{ I_m }{ 2000 }=0.238$[A]
答え (4)
2003年(平成15年)問12
変電所から三相3線式1回線の専用配電線で受電している需要家がある。この配電線路の電線1条当たりの抵抗及びリアクタンスの値は、それぞれ 3[Ω]及び 5[Ω]である。この需要家の使用電力が 8,000[kW]、負荷の力率が 0.8(遅れ)であるとき、次の(a)及び(b)に答えよ。
(a) 需要家の受電電圧が 20[kV]のとき、変電所引出口の電圧[kV]の値として、最も近いのは次のうちどれか。
(1) 21.6 (2) 22.2 (3) 22.7 (4) 22.9 (5) 23.1
(b) 需要家にコンデンサを設置して、負荷の力率を 0.95 (遅れ)に改善するとき、この配電線の電圧降下の値[V]の、コンデンサ設置前の電圧降下の値[V]に対する比率[%]の値として、最も近いのは次のうちどれか。
ただし、この需要家の受電電圧[kV]は、コンデンサ設置前と同一の 20[kV]とする。
(1) 66.6 (2) 68.8 (3) 75.5 (4) 81.7 (5) 97.0
2003年(平成15年)問12 過去問解説
(a) 受電電力を $P$[W]、受電端電圧を $V_r$[V]、線路電流を $I$[A]、負荷の力率を $cosθ$ とすると、
$P=\sqrt{3}V_rIcosθ$
$8000×10^3=\sqrt{3}×20×10^3×I×0.8$
$I=288.7$[A]
変電所引出口の電圧 $V_s$[kV]は、電圧降下の近似式より
$\begin{eqnarray}V_s&=&V_r+\sqrt{3}I(Rcosθ+Xsinθ)\\&=&20×10^3+\sqrt{3}×288.7(3×0.8+5×0.6)\\&=&22.7[kV]\end{eqnarray}$
答え (3)
(b) 力率 0.95 のときの線路電流を $I’$[A]とすると、有効電力には変化がないので、
$P=\sqrt{3}V_rIcosθ$
$8000×10^3=\sqrt{3}×20×10^3×I’×0.95$
$I’=243.1$[A]
電圧降下は、$V_s-V_r=\sqrt{3}I(Rcosθ+Xsinθ)$ ですので、
$\displaystyle \frac{ \sqrt{3}×243.1(3×0.95+5×\sqrt{1-0.95^2}) }{ \sqrt{3}×288.7(3×0.8+5×0.6) }×100=68.8$[%]
答え (2)
2005年(平成17年)問12
図に示すような線間電圧 $V$[V]、周波数 $f$[Hz]の対称三相3線式低圧電路があり、変圧器二次側の一端子にB種接地工事が施されている。この電路の1相当たりの対地静電容量を $C$[F]、B種接地工事の接地抵抗値を $R_B$[Ω]とするとき、次の(a)及び(b)に答えよ。
ただし、上記以外のインピーダンスは無視するものとする。
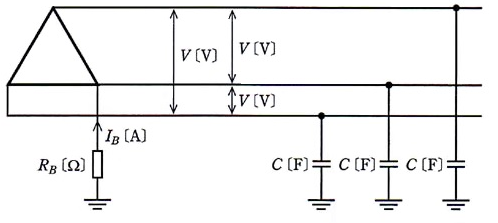
(a) B種接地工事の接地線に常時流れる電流 $I_B$[A]の大きさを表す式として、正しいのは次のうちどれか。
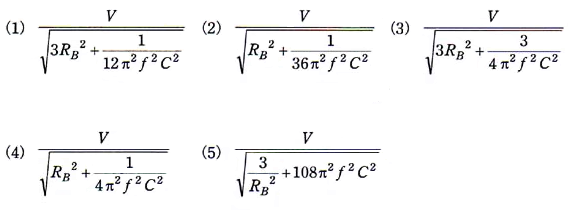
(b) 線間電圧 $V$ を 200[V]、周波数 $f$ を 50[Hz]、接地抵抗値 $R_B$を 10[Ω]、対地静電容量 $C$ を 1[μF]とするとき、上記(a)の電流 $I_B$[mA]の大きさとして、最も近いのは次のうちどれか。
(1) 1160 (2) 188 (3) 108 (4) 65.9 (5) 38.1
2005年(平成17年)問12 過去問解説
(a) 対地電圧 $E$[V]とすると、$E=\displaystyle \frac{V }{\sqrt{3}}$[V]ですので、元の回路の等価回路は次のようになります。
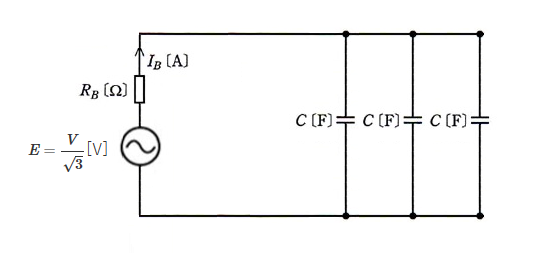
したがって、
$\begin{eqnarray}I_B=\displaystyle \frac{E}{\dot{Z}}&=&\displaystyle \frac{\displaystyle \frac{V }{\sqrt{3}}} {\sqrt{{R_B}^2+\left(\displaystyle \frac{1 }{2πf3C}\right)^2}}\\\\&=&\displaystyle \frac{\displaystyle \frac{V }{\sqrt{3}}} {\sqrt{{R_B}^2+\displaystyle \frac{1 }{36π^2f^2C^2}}}\\\\&=&\displaystyle \frac{V} {\sqrt{3{R_B}^2+\displaystyle \frac{1 }{12π^2f^2C^2}}}\end{eqnarray}$
答え (1)
(b) (a) の解答より
$\begin{eqnarray}I_B&=&\displaystyle \frac{V} {\sqrt{3{R_B}^2+\displaystyle \frac{1 }{12π^2f^2C^2}}}\\\\&=&\displaystyle \frac{200} {\sqrt{3×{10}^2+\displaystyle \frac{1 }{12π^2×50^2×(1×10^{-6})^2}}}\\\\&=&\displaystyle \frac{200} {\sqrt{300+\displaystyle \frac{1 }{3π^2×10^{-8}}}}\\\\&=&0.108=108[mA]\end{eqnarray}$
答え (3)
2006年(平成18年)問13
三相3線式配電線路から 6600[V]で受電している需要家がある。この需要家から配電系統へ流出する第5調波電流を算出するのあたり、次の(a)及び(b)に答えよ。
ただし、需要家の負荷設備は定格容量 500[kVA]の三相機器のみで、力率改善用として 6[%]直列リアクトル付きコンデンサ設備が設置されており、この三相機器(以下、高調波発生機器という。)から発生する第5調波電流は、負荷設備の定格電流に対し 15[%]とする。
また、受電点よりみた配電線路側の第n波長に対するインピーダンスは 10[MVA]基準で $j6×n$[%]、コンデンサ設備のインピーダンスは 10[MVA]基準で $j50×(6×n-\displaystyle \frac{100 }{ n })$[%]で表され、高調波発生器は定電流源とみなせるものとし、次のような等価回路で表すことができる。
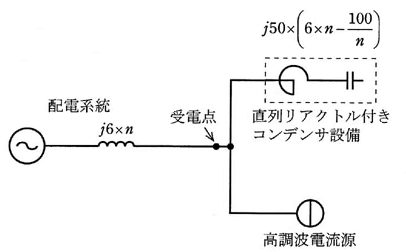
(a) 高調波発生器から発生する第5調波電流の受電点電圧に換算した電流[A]の値として、最も近いのは次のうちどれか。
(1) 1.3 (2) 6.6 (3) 11.4 (4) 32.8 (5) 43.7
(b) 受電点から配電系統に流出する第5調波電流[A]の値として、最も近いのは次のうちどれか。
(1) 1.2 (2) 6.2 (3) 10.8 (4) 30.9 (5) 41.2
2006年(平成18年)問13 過去問解説
(a) 定格容量を $P_n$[kVA]、定格電圧を $V$[kV]定格電流を$I_n$[A]とすると、
$P_n=\sqrt{3}VI_n$
$I_n=\displaystyle \frac{P_n}{\sqrt{3}V}=43.8$[A]
第5調波電流 $I_5$[A]は、負荷設備の定格電流に対し 15[%]ですので、
$I_5=I_n×0.15=6.6$[A]
答え (2)
(b) 第5調波電流 $I_5$[A]は、配電系統に流出する第5調波電流 $I_{5S}$[A]と、コンデンサ設備に流出する第5調波電流 $I_{5C}[A]$ に分流しますので、
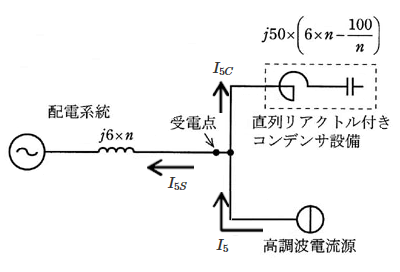
$\begin{eqnarray}I_{5S}&=&I_5×\displaystyle \frac{j50×(6×n-\displaystyle \frac{100 }{ n })}{j6×n+j50×(6×n-\displaystyle \frac{100 }{ n })}\\\\&=&6.6×\displaystyle \frac{j50×(6×5-\displaystyle \frac{100 }{ 5 })}{j6×5+j50×(6×5-\displaystyle \frac{100 }{ 5 })}\\\\&=&6.2[A]\end{eqnarray}$
答え (2)
2009年(平成21年)問11
図に示すような、相電圧 $E$[V]、周波数 $f$[Hz]の対称三相3線式低圧電路があり、変圧器の中性点に B種接地工事が施されている。B種接地工事の接地抵抗値を $R_B$[Ω]、電路の一相当たりの対地静電容量を $C$[F]とする。
この電路の絶縁抵抗が劣化により、電路の一相のみが絶縁抵抗値 $R_G$[Ω]に低下した。このとき、次の(a)及び(b)に答えよ。
ただし、上記以外のインピーダンスは無視するものとする。
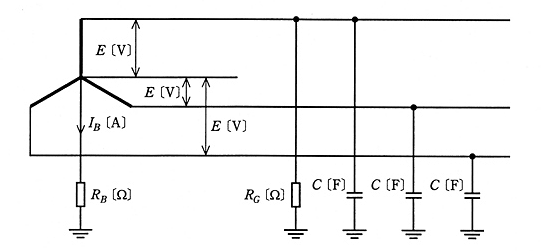
(a) 劣化により一相のみが絶縁抵抗値 $R_G$[Ω]に低下したとき、B種接地工事の接地線に流れる電流の大きさを $I_B$[A]とする。この $I_B$ を表す式として、正しいのは次のうちどれか。
ただし、他の相の対地コンダクタンスは無視するものとする。
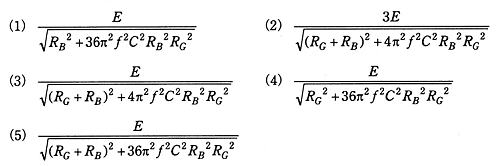
(b) 相電圧 $E$ を 100[V]、周波数 $f$ を 50[Hz]、対地静電容量 $C$ を 0.1[μF]、絶縁抵抗値 $R_G$ を 100[Ω]、接地抵抗値 $R_B$ を 15[Ω]とするとき、上記(a)の $I_B$ の値として、最も近いのは次のうちどれか。
(1) 0.87 (2) 0.99 (3) 1.74 (4) 2.61 (5) 6.67
2009年(平成21年)問11 過去問解説
(a) 一相分について考えると等価回路は次のようになります。
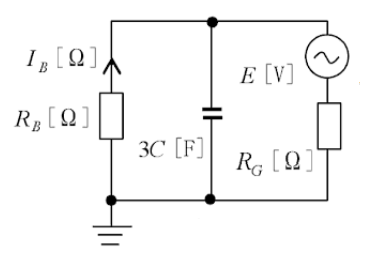
回路のインピーダンスを $\dot{Z}$ とすると、
$\dot{Z}=R_G+\displaystyle \frac{R_B×\displaystyle \frac{1}{jω3C}}{R_B+\displaystyle \frac{1}{jω3C}}$
B種接地工事の接地線に流れる電流 $\dot{I_B}$[A]は、電流の分流式より、
$\begin{eqnarray}\dot{I_B}&=&\displaystyle \frac{E}{\dot{Z}}×\displaystyle \frac{\displaystyle \frac{1}{jω3C}}{R_B+\displaystyle \frac{1}{jω3C}}\\\\&=&\displaystyle \frac{E}{R_G+\displaystyle \frac{R_B×\displaystyle \frac{1}{jω3C}}{R_B+\displaystyle \frac{1}{jω3C}}}×\displaystyle \frac{\displaystyle \frac{1}{jω3C}}{R_B+\displaystyle \frac{1}{jω3C}}\\\\&=&\displaystyle \frac{\displaystyle \frac{1}{jω3C}}{R_G\left(R_B+\displaystyle \frac{1}{jω3C}\right)+R_B×\displaystyle \frac{1}{jω3C}}E\\\\&=&\displaystyle \frac{E}{R_G+R_B+j3ωCR_BR_G}\end{eqnarray}$
したがって、電流の大きさを $I_B$[A]は、
$\begin{eqnarray}I_B&=&\displaystyle \frac{E}{\sqrt{(R_G+R_B)^2+(3ωCR_BR_G)^2}}\\\\&=&\displaystyle \frac{E}{\sqrt{(R_G+R_B)^2+36π^2f^2C^2R_B^2R_G^2}}\end{eqnarray}$
答え (5)
(b) (a) の解答より
$\begin{eqnarray}I_B&=&\displaystyle \frac{E}{\sqrt{(R_G+R_B)^2+36π^2f^2C^2R_B^2R_G^2}}\\\\&=&\displaystyle \frac{100}{\sqrt{(100+15)^2+36π^2×50^2×(0.1×10^{-6})^2×15^2×100^2}}\\\\&=&0.87[A]\end{eqnarray}$
答え (1)
2009年(平成21年)問13
図は、三相 210[V]低圧幹線の計画図の一部である。図の低圧配電盤から分電盤に至る低圧幹線に施設する配線用遮断器に関して、次の(a)及び(b)に答えよ。
ただし、基準容量 200[kV・A]・基準電圧 210[V]として、変圧器及びケーブルの各百分率インピーダンスは次のとおりとし、変圧器より電源側及びその他記載の無いインピーダンスは無視するものとする。
変圧器の百分率抵抗降下 1.4[%]及び百分率リアクタンス降下 2.0[%]
ケーブルの百分率抵抗降下 8.8[%]及び百分率リアクタンス降下 2.8[%]
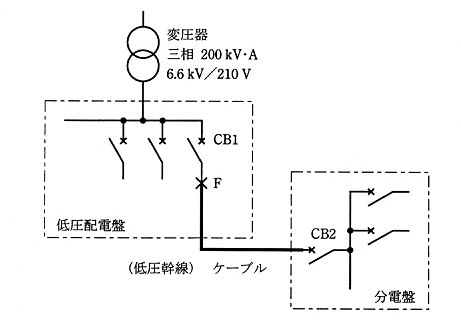
(a) F点における三相短絡電流[kA]の値として、最も近いのは次のうちどれか。
(1) 20 (2) 23 (3) 26 (4) 31 (5) 35
(b) 配電線用遮断器 CB1 及び CB2 の遮断容量[kA]の値として、最も適切な組み合わせは次のうちどれか。
ただし、CB1 と CB2 は、三相短絡電流の値の直近上位の遮断容量[kA] の配線用遮断器を選択するものとする。
| CB1の遮断容量[kA] | CB2の遮断容量[kA] | |
| (1) | 5 | 2.5 |
| (2) | 10 | 2.5 |
| (3) | 22 | 5 |
| (4) | 25 | 5 |
| (5) | 35 | 10 |
2009年(平成21年)問13 過去問解説
(a) 基準容量を $P_n$[VA]、基準電圧を $V_n$[V]、定格電流を$I_n$[A]とすると、
$P_n=\sqrt{3}V_nI_n$
三相短絡電流を$I_S$[A]とすると、
$\begin{eqnarray}I_S&=&\displaystyle \frac{100}{%Z}×I_n\\\\&=&\displaystyle \frac{100P_n}{\sqrt{3}V_n×%Z}\\\\&=&\displaystyle \frac{100×200×10^3}{\sqrt{3}×210×\sqrt{1.4^2+2.0^2}}\\\\&=&22550[A]≒23[kA]\end{eqnarray}$
答え (2)
(b) 分電盤の三相短絡電流を ${I_S}’$[A]とすると、ケーブルの $%Z$ も考慮しますので、
$\begin{eqnarray}{I_S}’&=&\displaystyle \frac{100}{%Z}×I_n\\\\&=&\displaystyle \frac{100P_n}{\sqrt{3}V_n×%Z}\\\\&=&\displaystyle \frac{100×200×10^3}{\sqrt{3}×210×\sqrt{(1.4+8.8)^2+(2.0+2.8)^2}}\\\\&=&4883[A]\end{eqnarray}$
答え (4)
2010年(平成22年)問11
図のような自家用電気施設の供給系統において、変電室変圧器二次側(210[V])で 三相短絡事故が発生した場合,次の(a)及び(b)に答えよ。
ただし,受電電圧 6600[V]、三相短絡事故電流 $I_S$=7[kA]とし、変流器 CT-3 の変流 比は、75A/5A とする。
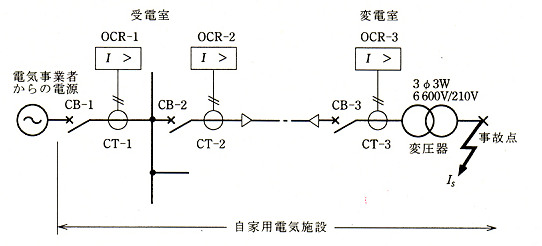
(a) 事故時における変流器 CT-3 の二次電流[A]の値として、最も近いのは次のうちどれか。
(1) 5.6 (2) 7.5 (3) 11.2 (4) 14.9 (5) 23
(b) この事故における保護協調において、施設内の過電流継電器の中で最も早い動作が求められる過電流継電器(以下、OCR-3 という。)の動作時間[秒]の値として、最も近いのは次のうちどれか。
ただし,OCR-3 の動作時間演算式は[秒]とする。この演算式における $T=\displaystyle \frac{80 }{ (N^2-1) }×\displaystyle \frac{D }{ (10) }$ [秒]とする。この演算式における $T$ は OCR-3 の動作時間[秒]、 $N$ はOCR-3 の電流整定値に対する入力電流値の倍数を示し、$D$ はダイヤル(時限)整定値である。
また、CT-3 に接続された OCR-3 の整定値は次のとおりとする。

(1) 0.4 (2) 0.7 (3) 1.2 (4) 1.7 (5) 3.4
2010年(平成22年)問11 過去問解説
(a) CT-3 の二次電流を $I_3$[A]とすると、
$I_3=7000×\displaystyle \frac{210}{6600}×\displaystyle \frac{5}{75}=14.9$[A]
答え (4)
(b) 題意より、
$\begin{eqnarray}T&=&\displaystyle \frac{80 }{ (N^2-1) }×\displaystyle \frac{D }{ (10) }\\\\&=&\displaystyle \frac{80 }{ (\displaystyle \frac{14.9}{3}^2-1) }×\displaystyle \frac{2 }{ (10) }\\\\&=&0.676\end{eqnarray}$
答え (2)
2011年(平成23年)問13
図は、電圧 6600[V]、周波数 50[Hz]、中性点非接地方式の三相3線式配電線路及び需要家Aの高圧地絡保護システムを簡易に表した単線図である。 次の(a)及び(b)の問に答えよ。
ただし、図で使用している主要な文字記号は付表のとおりとし、$C_1=3.0$[μF],$C_2=0.015$[μF]とする。なお、図示されていない線路定数及び配電用変電所の制限抵抗は無視するものとする。
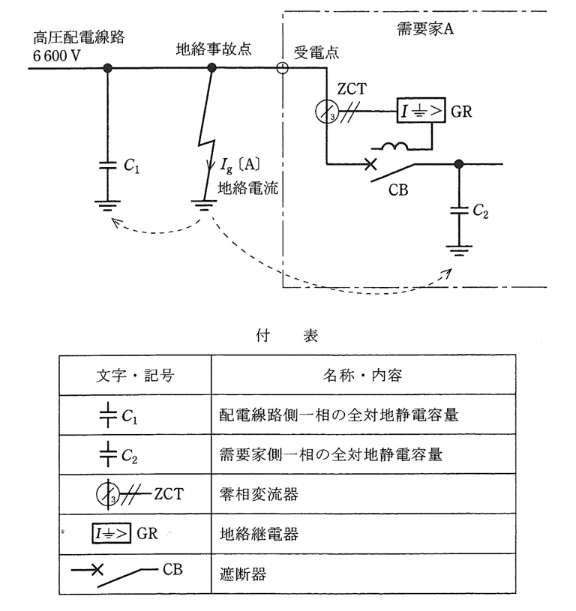
(a) 図の配電線路において、遮断器CBが「入」の状態で地絡事故点に一線完全地絡事故が発生した場合の地絡電流 $I_g$[A]の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、間欠アークによる高調波の影響は無視できるものとする。
(1) 4 (2) 7 (3) 11 (4)19 (5) 33
(b) 図のような高圧配電線路に接続される需要家が、需要家構内の地絡保護のために設置する継電器の保護強調に関する記述として誤っているものを次の(1)~(5)のうちから一つ選べ。
なお、記述中「不必要動作」とは、需要家の構外事故において継電器が動作することをいう。
- 需要家が設置する地絡継電器の動作電流及び動作時限整定値は、配電用変電所の整定値より小さくする必要がある。
- 需要家の構内高圧ケーブルが極めて短い場合、需要家が設置する継電器が無方向性地絡継電器でも、不必要動作の発生は少ない。
- 需要家が地絡方向継電器を設置すれば、構内高圧ケーブルが長い場合でも不必要動作は防げる。
- 需要家が地絡方向継電器を設置した場合、その整定値は配電用変電所との保護協調に関し動作時限のみ考慮すればよい。
- 地絡事故電流の大きさを考える場合、地絡事故が間欠アーク現象を伴うことを想定し、波形ひずみによる高調波の影響を考慮する必要がある。
2011年(平成23年)問13 過去問解説
(a) 対地電圧 $E$[V]とすると、$E=\displaystyle \frac{V }{\sqrt{3}}$[V]ですので、元の回路の等価回路は次のようになります。
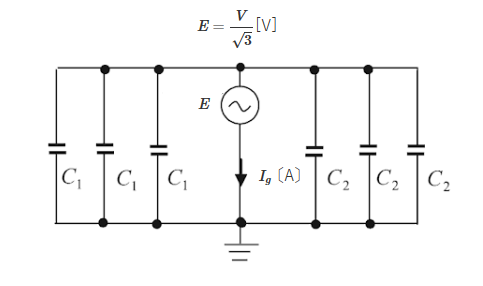
したがって、
$\begin{eqnarray}I_g=\displaystyle \frac{E}{\dot{Z}}&=&\displaystyle \frac{\displaystyle \frac{V }{\sqrt{3}}} {\displaystyle \frac{1}{ω(3C_1+3C_2)}}\\\\&=&\displaystyle \frac{V }{\sqrt{3}}ω(3C_1+3C_2)\\\\&=&\displaystyle \frac{6600 }{\sqrt{3}}×2×π×50×3(3×10^{-6}+0.015×10^{-6})\\\\&=&10.8[A]\end{eqnarray}$
答え (3)
(b) (4)の記述「需要家が地絡方向継電器を設置した場合、その整定値は配電用変電所との保護協調に関し動作時限のみ考慮すればよい。」で、これは時限整定と地絡電流値についても整定する必要があります。したがって間違った記述となります。
答え (4)
2013年(平成25年)問11
高圧進相コンデンサの劣化診断について、次の(a)及び(b)の問に答えよ。
(a) 三相3線式 50[Hz] 、使用電圧 6.6[kV]の高圧電路に接続された定格電圧 6.6[kV]、定格容量 50 [kvar] (Y 結線、一相 2 素子) の高圧進相コンデンサがある。その内部素子の劣化度合い点検のため、運転電流を高圧クランプメータで定期的に測定していた。
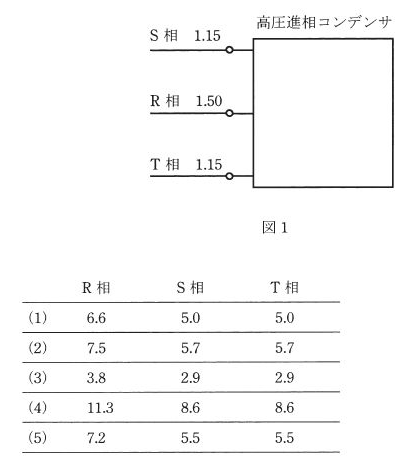
ある日の測定において、測定電流[A]の定格電流[A]に対する比は、図1のとおりであった。測定電流[A]に最も近い数値の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、直列リアクトルはないものとして計算せよ。
(b) (a)の測定により、劣化による内部素子の破壊(短絡)が発生していると判断し、機器停止のうえ各相間の静電容量を 2 端子測定法(1 端子開放で測定)で測定した。
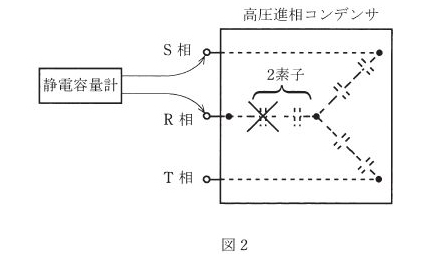
図 2のとおりの内部結線における素子破壊 (素子極間短絡) が発生しているとすれば、静電容量測定結果の記述として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、図中 ☓ 印は、破壊素子を表す。
- R-S 相間の測定値は、最も小さい。
- S-T 相間の測定値は、最も小さい。
- T-R 相間は、測定不能である。
- R-S 相間の測定値は、S-T 相間の測定値の約 75[%]である。
- R-S 相間と S-T 相間の測定値は、等しい。
2013年(平成25年)問11 過去問解説
(a) 定格電圧を $V_n$[V]、定格電流を$I_n$[A]、高圧進相コンデンサの容量を $Q$[var]とすると、
$Q=\sqrt{3}V_nI_n$
$I_n=\displaystyle \frac{Q}{\sqrt{3}V_n}=\displaystyle \frac{50×10^3}{\sqrt{3}×6.6×10^3}=4.38$[A]
測定電流[A]の定格電流[A]に対する比が、示されていますので、求める各相に流れる測定電流[A]は、
R相:$4.38×1.5=6.57$[A]
S相:$4.38×1.15=5.04$[A]
T相:$4.38×1.15=5.04$[A]
答え (1)
(b) R-S相間の合成静電容量を $C_{RS}$[F]とすると、1素子が短絡されているので、
$C_{RS}=\displaystyle \frac{1}{\displaystyle \frac{1}{C}+\displaystyle \frac{1}{C}+\displaystyle \frac{1}{C}}=\displaystyle \frac{C}{3}$[F]
T-R相間の合成静電容量を $C_{TR}$[F]とすると、
$C_{TR}=\displaystyle \frac{1}{\displaystyle \frac{1}{C}+\displaystyle \frac{1}{C}+\displaystyle \frac{1}{C}+\displaystyle \frac{1}{C}}=\displaystyle \frac{C}{4}$[F]
したがって、(2)が適切になります。
答え (2)
2014年(平成26年)問13
三相3線式、受電電圧 6.6kV、周波数 50Hz の自家用電気設備を有する需要家が、直列リアクトルと進相コンデンサからなる定格設備容量 100kvar の進相設備を施設することを計画した。この計画におけるリアクトルには、当該需要家の遊休中の進相設備から直列リアクトルのみを流用することとした。施設する進相設備の進相コンデンサのインピーダンスを基準として、これを -j100% と考えて、次の(a)及び(b)の問に答えよ。

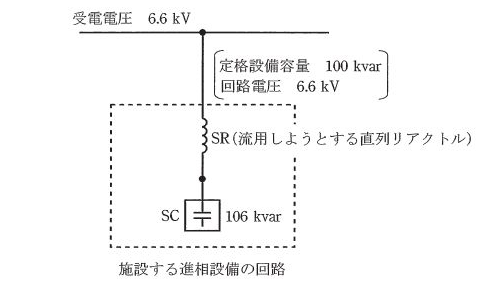
(a) 回路電圧 6.6kV のとき、施設する進相設備のコンデンサの端子電圧の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 6600 (2) 6875 (3) 7020 (4) 7170 (5) 7590
(b) この計画における進相設備の、第5調波の影響に関する対応について、正しいものを次の(1)~(5)のうちから一つ選べ。
- インピーダンスが 0% の共振状態に近くなり、過電流により流用しようとするリアクトルとコンデンサは 共に焼損のおそれがあるため、本計画の機器流用は危険であり、流用してはならない。
- インピーダンスが約 -j10% となり進み電流が多く流れ、流用しようとするリアクトルの高調波耐量が保証されている確認をしたうえで流用する必要がある。
- インピーダンスが約 +j10% となり遅れ電流が多く流れ、流用しようとするリアクトルの高調波耐量が保証されている確認をしたうえで流用する必要がある。
- インピーダンスが約 -j25% となり進み電流が流れ、流用しようとするリアクトルの高調波耐量を確認したうえで流用する必要がある。
- インピーダンスが約 +j25% となり遅れ電流が流れ、流用しようとするリアクトルの高調波耐量を確認したうえで流用する必要がある。
2014年(平成26年)問13 過去問解説
(a) 直列リアクトルは、進相コンデンサのインピーダンスの 6%ですので、施設する進相コンデンサのインピーダンスを基準にすると、直列リアクトルの %Z[%]は、
$ %Z_L=j6×\displaystyle \frac{106}{160}=j3.975$[%]
進相コンデンサの端子電圧 $\dot{V}_C$[V]は、
$\dot{V}_C=\displaystyle \frac{-j100}{-j100+j3.975}×6.6×10^3=6875$[V]
答え (2)
(b) 第5調波は、周波数が基本波の 5倍になる波形です。リアクトルのインピーダンス $ωL$ は、周波数が 5倍になればインピーダンスは5倍になります。コンデンサのインピーダンス $\displaystyle \frac{1}{ωC}$ は、周波数が 5倍になるとインピーダンスは $\displaystyle \frac{1}{5}$ 倍になります。
直列リアクトルの%Z:j3.975×5≒j20[%]
進相コンデンサの%Z:-j100÷5=j20[%]
合成%インピーダンスは、0になります。つまり直列共振状態になりますので、(1)が正しい記述となります。
答え (1)
2016年(平成28年)問13
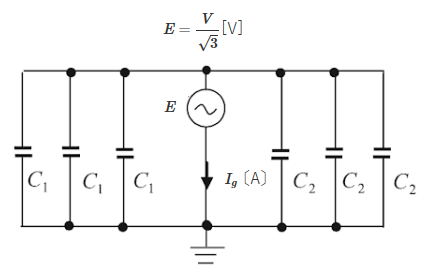
図は、線間電圧 $V$[V]、周波数 $f$ [Hz] の中性点非接地方式の三相3線式高圧配電線路及びある需要設備の高圧地絡保護システムを簡易に示した単線図である。高圧配電線路一相の全対地静電容量を $C_1$ [F] 、需要設備一相の全対地静電容量を $C_2 $ [F] とするとき、次の(a)及び(b)に答えよ。
ただし、図示されていない負荷、線路定数及び配電用変電所の制限抵抗は無視するものとする。
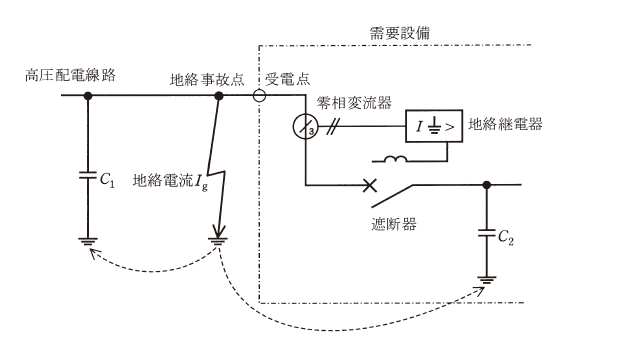
(a) 図の配電線路において、遮断器が「入」の状態で地絡事故点に一線完全地絡事故が発生し地絡電流 $I_g$[A]が流れた。このとき $I_g$ の大きさを表す式として正しいものは次のうちどれか。
ただし、間欠アークによる影響等は無視するものとし、この地絡事故によって遮断器は遮断しないものとする。
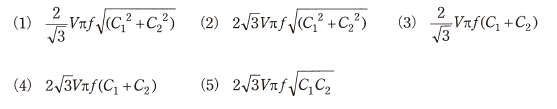
(b) 上記(a)の地絡電流 $I_g$ は高圧配電線路側と需要設備側に分流し、需要設備側に分流した電流は零相変流器を通過して検出される。上記のような需要設備構外の事故に対しても、零相変流器が検出する電流の大きさによっては地絡継電器が不必要に動作する場合があるので注意しなければならない。地絡電流 $I_g$ が高圧配電線路側と需要設備側に分流する割合は $C_1$ と $C_2$ の比によって決まるものとしたとき、$I_g$ のうち需要設備の零相変流器で検出される電流の値 [mA] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、$V=6600V$、$f=60Hz$、$C_1=2.3μF$、$C_2=0.02μF$とする。
(1) 54 (2) 86 (3) 124 (4) 152 (5) 256
2016年(平成28年)問13 過去問解説
(a) 対地電圧 $E$[V]とすると、$E=\displaystyle \frac{V }{\sqrt{3}}$[V]ですので、一線完全地絡事故時の等価回路は次のようになります。
したがって、
$\begin{eqnarray}I_g=\displaystyle \frac{E}{\dot{Z}}&=&\displaystyle \frac{\displaystyle \frac{V }{\sqrt{3}}} {\displaystyle \frac{1}{ω(3C_1+3C_2)}}\\\\&=&\displaystyle \frac{V }{\sqrt{3}}×2πf(3C_1+3C_2)\\\\&=&2\sqrt{3}Vπf(C_1+C_2)\end{eqnarray}$
答え (4)
(b) (a)の解答より
$\begin{eqnarray}I_g&=&2\sqrt{3}Vπf(C_1+C_2)\\\\&=&2\sqrt{3}×6600×π×60×(2.3×10^{-6}+0.02×10^{-6})\\\\&=&9.98[A]\end{eqnarray}$
需要設備の零相変流器で検出される電流の値 [mA] は、
$\displaystyle \frac{C_2}{C_1+C_2}×I_g=\displaystyle \frac{0.02×10^{-6}}{2.3×10^{-6}+0.02×10^{-6}}×9.98=86$ [mA]
答え (2)
2017年(平成29年)問12
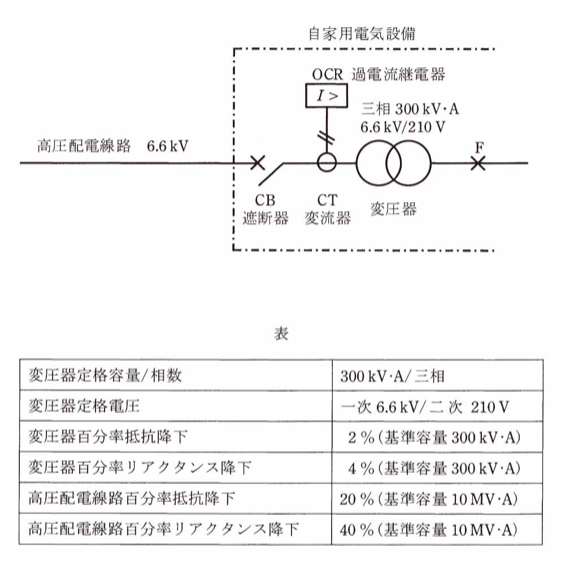
図に示す自家用電気設備で変圧器二次側( 210V 側)F点において三相短絡事故が発生した。次の(a)及び(b)の問に答えよ。
ただし、高圧配電線路の送り出し電圧は 6.6kV とし、変圧器の仕様及び高圧配電線路のインピーダンスは表のとおりとする。なお、変圧器二次側からF点までのインピーダンス、その他記載の無いインピーダンスは無視するものとする。
(a) F点における三相短絡電流の値 [kA] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.2 (2) 1.7 (3) 5.2 (4) 11.7 (5) 14.2
(b) 変圧器一次側( 6.6kV 側)に変流器CTが接続されており、CT二次電流が過電流継電器OCRに入力されているとする。三相短絡事故発生時のOCR入力電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、CTの変流比は 75A/5A とする。
(1) 12 (2) 18 (3) 26 (4) 30 (5) 42
2017年(平成29年)問12 過去問解説
(a) 基準容量を $P_n$[VA]、基準電圧を $V_n$[V]、定格電流を $I_n$[A]とすると、
$P_n=\sqrt{3}V_nI_n$
三相短絡電流を $I_S$[A]とすると、
$\begin{eqnarray}I_S&=&\displaystyle \frac{100}{%Z}×I_n\\\\&=&\displaystyle \frac{100P_n}{\sqrt{3}V_n×%Z}\\\\&=&\displaystyle \frac{100×300×10^3}{\sqrt{3}×210×\sqrt{(2+0.6)^2+(4+1.2)^2}}\\\\&=&14213[A]\end{eqnarray}$
答え (5)
(b) 三相短絡電流が 14.2[kA]ですので、変圧器一次側で換算した $I_1$[A]は、
$\displaystyle \frac{6600}{210}=\displaystyle \frac{14200}{I_1}$
$I_1=451.8$[A]
CTの変流比は 75A/5A ですので、
$\displaystyle \frac{75}{5}=\displaystyle \frac{451.8}{I}$
$I=30$[A]
答え (4)





