第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、電気に関する基礎理論「電線の抵抗と抵抗率」について、解説しています。
電線の抵抗と抵抗率
電流の流れにくさを表すことを電気抵抗(抵抗)といいます。抵抗の単位はオーム(記号:Ω)です。 抵抗が小さいと電流は流れやすくなり、抵抗が大きいと電流は流れにくくなります。
電気抵抗の大きさは、導線の長さに比例し、断面積に反比例します。これを式に表すと次のようになります。
電気抵抗と導線の長さと断面積の関係
$R=ρ\displaystyle\frac{L}{A}$[Ω]
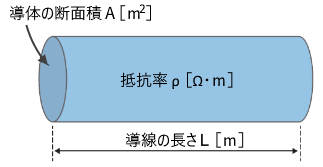
$R$:電気抵抗[Ω]
$ρ$:電気抵抗率[Ω · m]
$L$:導線の長さ[m]
$A$:導線の断面積[m2]
電気抵抗率$ρ$(読み:ロー)とは、物質がもつ電気の流れにくさを表す値で、単位は[Ω · m]です。銅や銀などの導体は電気抵抗率が低く、ガラスやプラスチックなどの絶縁体は電気抵抗率が高くなります。また、金属などの導体は温度が上がると抵抗率も大きくなる性質があります。
電気に関する基礎理論:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 電線の抵抗と抵抗率①
抵抗率 ρ[Ω · m]、直径 D[mm]、長さ L[m]の導線の電気抵抗[Ω]を表す式は。
イ. $\displaystyle\frac{4ρL}{πD}×10^3$ ロ. $\displaystyle\frac{4ρL^2}{πD}×10^3$ ハ. $\displaystyle\frac{4ρL}{πD^2}×10^6$ 二. $\displaystyle\frac{ρL^2}{πD^2}×10^6$
導体の断面積を $A$[m2]とすると、導体は直径 $D$[mm]($1$mm$=10^{-3}$m)の円形ですので、
$A=π(\displaystyle\frac{D}{2}×10^{-3})^2=\displaystyle\frac{πD^2×10^{-6}}{4}$[m2]
導線の電気抵抗 $R$[Ω]は、
$R=ρ\displaystyle\frac{L}{A}=\displaystyle\frac{4ρL}{πD^2}×10^{6}$[Ω]
答え(ハ)
2007年(平成19年)問2
2010年(平成22年)問3
2015年(平成27年)下期 問3
2017年(平成29年)下期 問3
問2 電線の抵抗と抵抗率②
電気抵抗 R[Ω]、直径 D[mm]、長さ L[m]の導線の抵抗率[Ω · m]を表す式は。
イ. $\displaystyle\frac{πD^2R}{4L×10^6}$ ロ. $\displaystyle\frac{πD^2R}{L^2×10^6}$ ハ. $\displaystyle\frac{πDR}{4L×10^6}$ 二. $\displaystyle\frac{πDR}{4L^2×10^6}$
導体の断面積を $A$[m2]とすると、導体は直径 $D$[mm]($1$mm$=10^{-3}$m)の円形ですので、
$A=π(\displaystyle\frac{D}{2}×10^{-3})^2=\displaystyle\frac{πD^2×10^{-6}}{4}$[m2]
導線の抵抗率 $ρ$[Ω · m]は、
$R=ρ\displaystyle\frac{L}{A}$[Ω]
$ρ=\displaystyle\frac{RA}{L}=\displaystyle\frac{πD^2R}{4L×10^{6}}$[Ω · m]
答え(イ)
2014年(平成26年)上期 問4
問3 電線の抵抗と抵抗率③
直径 1.6[mm]、長さ 8[m]の軟銅線と電気抵抗値が等しくなる直径 3.2[mm]の軟銅線の長さ[m]は。
ただし、軟銅線の温度、抵抗率は同一とする。
イ. 4 ロ. 8 ハ. 16 二. 32
導体の断面積を $A$[m2]とすると、導体は直径 $D$[mm]($1$mm$=10^{-3}$m)の円形ですので、
$A=π(\displaystyle\frac{D}{2}×10^{-3})^2=\displaystyle\frac{πD^2×10^{-6}}{4}$[m2]
銅線の電気抵抗 $R$[Ω]は、
$R=ρ\displaystyle\frac{L}{A}=\displaystyle\frac{4ρL}{πD^2}×10^{6}$[Ω]
軟銅線の電気抵抗は直径 $D$ の2乗($D^2$)に反比例しますので、直径が2倍($2D$)になると、$(2D)^2=4D^2$ に反比例します。
題意は、直径 1.6[mm]の軟銅線と直径 3.2[mm]の軟銅線の電気抵抗値が等しくなる長さを求めることですので、直径 3.2[mm]の軟銅線の長さは、直径 1.6[mm]の軟銅線長さより4倍長くなると、電気抵抗値が等しくなります。
$8×4=32$[m]
答え(二)
2008年(平成20年)問2
2012年(平成24年)上期 問3
問4 電線の抵抗と抵抗率④
直径2.6[mm]、長さ10[m]の銅導線と抵抗値が最も近い銅導線は。
- 直径1.6[mm]、長さ20[m]
- 断面積5.5[mm2]、長さ10[m]
- 直径3.2[mm]、長さ5[m]
- 断面積8[mm2]、長さ10[m]
導体の電気抵抗を $R$[Ω]、抵抗率を $ρ$[Ω · m]、直径を $D$[mm]、長さを $L$[m]、断面積を $A$[m2]とすると、
$R=ρ\displaystyle\frac{L}{A}=\displaystyle\frac{4ρL}{πD^2}×10^{6}$
$=\displaystyle\frac{4ρ×10}{π×2.6^2}×10^{6}≒1.88ρ×10^{6}$[Ω]
イ.$R=\displaystyle\frac{4ρ×20}{π×1.6^2}×10^{6}≒9.95ρ×10^{6}$[Ω]
ロ.$R=ρ×\displaystyle\frac{10}{5.5×(10^{-3})^2}≒1.82×10^{6}$[Ω]
ハ.$R=\displaystyle\frac{4ρ×5}{π×3.2^2}×10^{6}≒0.622ρ×10^{6}$[Ω]
二.$R=ρ×\displaystyle\frac{10}{8×(10^{-3})^2}≒1.25×10^{6}$[Ω]
答え(ロ)
2009年(平成21年)問4
2013年(平成25年)下期 問3
2014年(平成26年)下期 問3 類似
2016年(平成28年)下期 問3
2018年(平成30年)下期 問3
2019年(令和元年)下期 問2
問5 電線の抵抗と抵抗率⑤
A、B 2 本の同材質の銅線がある。A は直径 1.6[mm],長さ 20[m]、B は直径 3.2 [mm],長さ 40[m]である。A の抵抗は B の抵抗の何倍か。
イ. 1 ロ. 2 ハ. 3 二. 4
導体の電気抵抗を $R$[Ω]、抵抗率を $ρ$[Ω · m]、直径を $D$[mm]、長さを $L$[m]、断面積を $A$[m2]とすると、
$R=ρ\displaystyle\frac{L}{A}=\displaystyle\frac{4ρL}{πD^2}×10^{6}$
Aの抵抗 $R_A$[Ω]は
$R_A=\displaystyle\frac{4ρ×20}{π×1.6^2}×10^{6}=31.25\displaystyle\frac{ρ}{π}×10^{6}$[Ω]
Bの抵抗 $R_B$[Ω]は
$R_B=\displaystyle\frac{4ρ×40}{π×3.2^2}×10^{6}=15.625\displaystyle\frac{ρ}{π}×10^{6}$[Ω]
したがって、Aの抵抗はBの抵抗の2倍になります。
答え(ロ)
2011年(平成23年)上期 問1 類似
2013年(平成25年)上期 問2
2015年(平成27年)上期 問3
2017年(平成29年)上期 問3
問6 電線の抵抗と許容電流
ビニル絶縁電線(単心)の導体の直径をD、長さをLとするとき、この電線の抵抗と許容電流に関する記述として、誤っているものは。
- 電線の抵抗は、Lに比例する。
- 電線の抵抗は、D2に反比例する。
- 許容電流は、周囲の温度が上昇すると、大きくなる。
- 許容電流は、Dが大きくなると、大きくなる。
- 正しい記述です。
- 正しい記述です。
- 許容電流は、周囲の温度が上昇すると、小さくなる。
- 正しい記述です。
導体の電気抵抗を $R$[Ω]、抵抗率を $ρ$[Ω · m]、直径を $D$[mm]、長さを $L$[m]、断面積を $A$[m2]とすると、
$R=ρ\displaystyle\frac{L}{A}=\displaystyle\frac{4ρL}{πD^2}×10^{6}$
導体の電気抵抗が大きくなると、許容電流は小さくなります。一般に、抵抗は温度に比例して大きくなります。したがって、許容電流は、周囲の温度が上昇すると、小さくなります。
答え(ハ)
2006年(平成18年)問2
2011年(平成23年)下期 問1
2016年(平成28年)上期 問3 類似
2018年(平成30年)上期 問3
2019年(令和元年)上期 問2



