第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される過渡現象について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された過渡現象の過去問題も解説しています。
- 過渡現象とは?
- 時定数と仮想短絡・仮想開放
- 過渡現象の問題を解くポイント
- 電験三種-理論の過去問解説:過渡現象
- 2001年(平成13年)問5【電験理論の過去問題】
- 2002年(平成14年)問9【電験理論の過去問題】
- 2003年(平成15年)問9【電験理論の過去問題】
- 2004年(平成16年)問9【電験理論の過去問題】
- 2005年(平成17年)問9【電験理論の過去問題】
- 2006年(平成18年)問10【電験理論の過去問題】
- 2007年(平成19年)問10【電験理論の過去問題】
- 2008年(平成20年)問10【電験理論の過去問題】
- 2009年(平成21年)問10【電験理論の過去問題】
- 2010年(平成22年)問10【電験理論の過去問題】
- 2011年(平成23年)問10【電験理論の過去問題】
- 2012年(平成24年)問9【電験理論の過去問題】
- 電験三種 過去問解説 2013年(平成25年)問12
- 2014年(平成26年)問11【電験理論の過去問題】
- 2015年(平成27年)問10【電験理論の過去問題】
- 2016年(平成28年)問10【電験理論の過去問題】
- 2017年(平成29年)問10【電験理論の過去問題】
過渡現象とは?
コンデンサやコイルを含む回路に直流電源をつないだ場合、コンデンサやコイルには電気が充電され、回路に流れる電流が一定値になるまでには時間を要します。また、直流電源の代わりに抵抗を接続すると、充電されたコンデンサやコイルは放電を開始し、やがて回路に流れる電流は一定値になります。
このようなに、電流や電圧が一定の値になるまで変化する現象を「過渡現象」といい、過渡現象が起きている状態のことを「過渡状態」いいます。また、電流や電圧の変化が終わって一定の値になった状態を、「定常状態」といいます。
コンデンサに充電する時の過渡現象
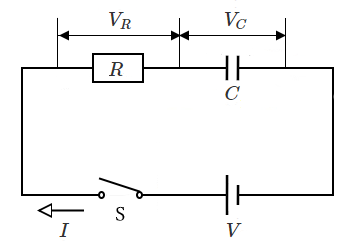
静電容量 $C$[F]のコンデンサ、抵抗 $R$[Ω]と起電力 $V$[V]の直流電源を直列に接続した回路です。
① スイッチ S を閉じると、回路に電流が流れ、コンデンサは徐々に充電されます。
② コンデンサが完全に充電されると、それ以上電流は流れなくなります。
①の電流が流れている状態が「過渡状態」で、②の電流が流れなくなった状態が「定常状態」です。
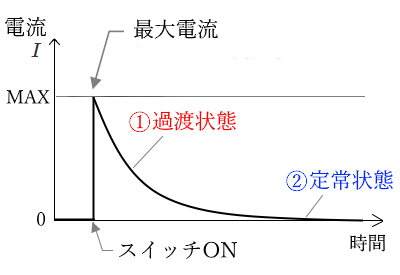
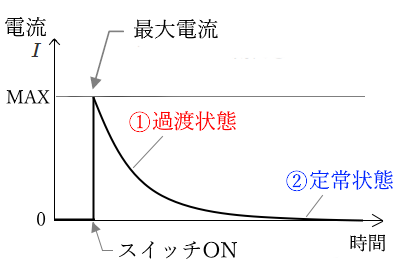
電流 $I$ のグラフ
回路に流れる電流 $I$ はスイッチSを入れた瞬間に最大電流が流れ、その後時間とともに減っていき、最後は 0 になります。
コンデンサが完全に充電されると、それ以上電流は流れなくなります。
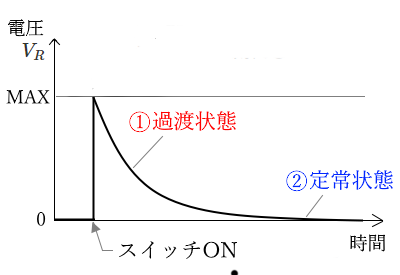
抵抗にかかる電圧 $V_R$ のグラフ
① 抵抗にかかる電圧 $V_R$ は、スイッチSを入れた瞬間は、抵抗両端の電圧 $V_R$ は最大となり、コンデンサが充電されるにつれて、電圧 $V_R$ は小さくなっていきます。
② コンデンサの電圧 $V_C$ が電源電圧 $V$ に等しくなると充電は終了し、電圧 $V_R$ は 0 になり、それ以降電圧は変化しなくなります。
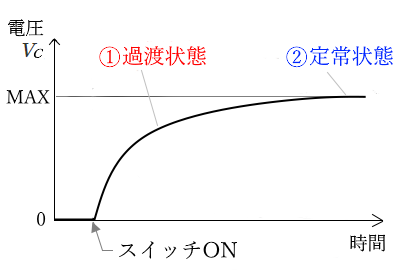
コンデンサにかかる電圧 $V_C$ のグラフ
① コンデンサにかかる電圧 $V_C$ は、スイッチSを入れた瞬間はコンデンサには電荷が溜まっていないので、コンデンサ両端の電圧 $V_C$ は 0 です。
電流が流れると、コンデンサの+側には+の電荷、-側には-の電荷が徐々に溜まっていき、電圧 $V_C$は大きくなっていきます。
② コンデンサが完全に充電されたとき、電圧 $V_C$ は最も大きくなり、電源電圧 $V$ と同じになります。
コンデンサが放電する時の過渡現象
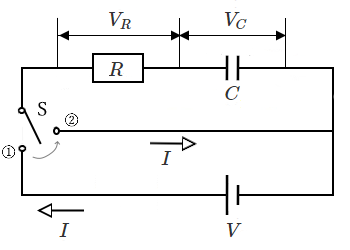
図のように接続された回路で、スイッチ S を①側に倒せば、コンデンサは充電します。次に、スイッチ S を②側に倒せば、コンデンサは放電します。
① コンデンサが放電している間は電流が流れ、この時の状態は「過渡状態」です。
② コンデンサの放電が終わり、電流が流れなくなった状態が「定常状態」になります。
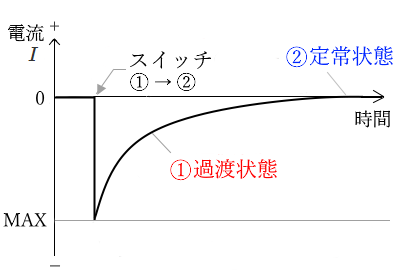
電流 $I$ のグラフ
① スイッチ S を①から②側に倒した瞬間は、充電の時とは逆向きの大きな電流が流れ、その後は徐々に小さくなります。
② コンデンサが完全に放電されると、電流は流れなくなります。
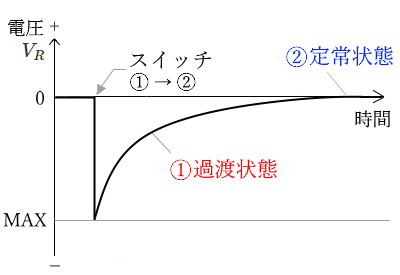
抵抗にかかる電圧 $V_R$ のグラフ
① 充電時と放電時で、電流の向きが逆になるため、抵抗にかかる電圧 $V_R$ も同じように逆になります。
② 充電時と同様に、抵抗にかかる電圧 $V_R$ の変化の様子は、電流 $I$ と同じになりますので、グラフも同じ
形になります。
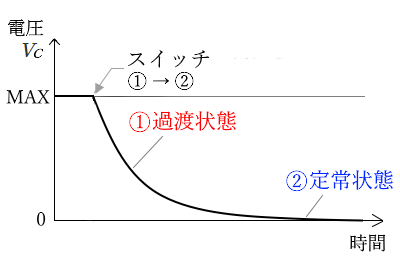
コンデンサにかかる電圧 $V_C$ のグラフ
① フルに充電された状態のコンデンサの電圧 $V_C$ は、電源と同じ電圧になります。これを放電させますので、徐々に電圧は低下していきます。
② コンデンサが完全に放電されると、電圧は 0 になります。
コイルに充電する時の過渡現象
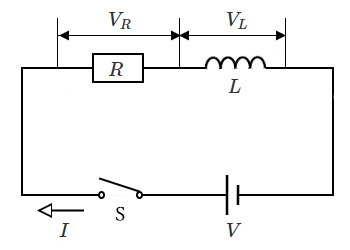
インダクタンス $L$[H]のコイル、抵抗 $R$[Ω]と起電力 $V$[V]の直流電源を直列に接続した回路です。
① スイッチ S を閉じると、回路に電流が流れようとしますが、コイルに逆起電力が発生して電流の流れを妨げるため、電源からの電流は流れません。時間経過とともに逆起電力は減っていき、電流は徐々に流れるようになります(過渡状態)。
② コイルが完全に充電されると、逆起電力はなくなり、電流が流れます(定常状態)。
電流 $I$ のグラフ
① スイッチを入れた瞬間は、コイルに電流は流れませんが、時間経過とともに徐々に流れるようになります。
② 一定時間経過すればコイルが完全に充電され、最大電流が流れるようになります。
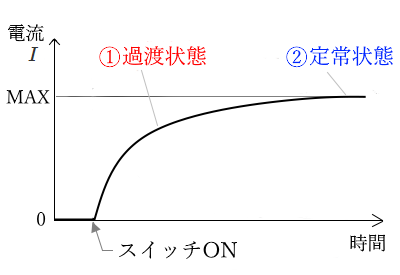
抵抗にかかる電圧 $V_R$ のグラフ
① スイッチを入れた瞬間は、コイルに電流は流れませんので、抵抗 $R$ に電圧はかかりません。時間経過とともに、徐々にコイルに流れる電流が増加すると、抵抗 $R$ にかかる電圧 $V_R$ も大きくなります。
② コイルに流れる電流が最大になると、$V_R$ も最大になります 。
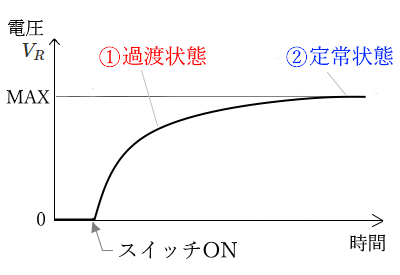
コイルにかかる電圧 $V_L$ のグラフ
① スイッチを入れた瞬間は、コイルの逆起電力が最大になるので、コイルにかかる電圧 $V_L$ は最大になります。時間経過とともに、徐々にコイルに流れる電流が増加していくため、$V_L$ は減っていきます。
② コイルに流れる電流が最大になると、$V_L$ は 0 になります。
コイルが放電する時の過渡現象
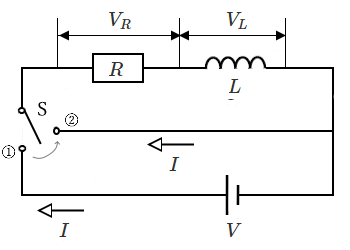
図のように接続された回路で、スイッチ S を①側に倒せば、コイルは充電します。次に、スイッチ S を②側に倒せば、コイルは放電します。
① コイルが放電している間は電流が流れ、この時の状態は「過渡状態」です。
② コイルの放電が終わり、電流が流れなくなった状態が「定常状態」になります。
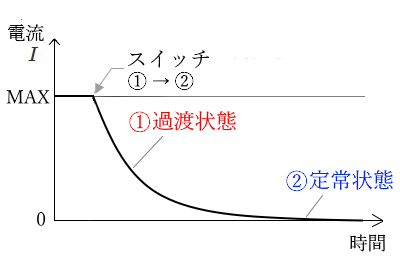
電流 $I$ のグラフ
① スイッチ S を①から②側に倒した瞬間は、充電の時と同じ向きに大きな電流が流れ、その後は徐々に小さくなります。
② コイルが完全に放電されると、電流は流れなくなります。
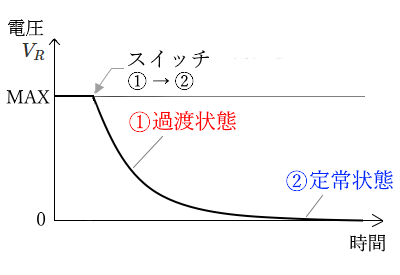
抵抗にかかる電圧 $V_R$ のグラフ
① 放電時の、抵抗にかかる電圧 $V_R$ は、スイッチ S を①から②側に倒した瞬間は、大きな電流が流れますので、最大になり、その後は徐々に小さくなります。
② コイルが完全に放電されると、電流は流れなくなり、 $V_R$ も 0 になります。
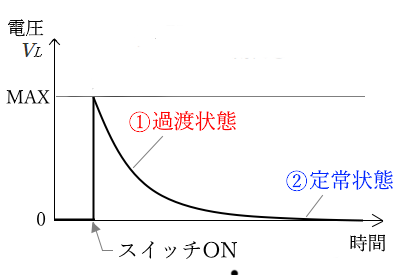
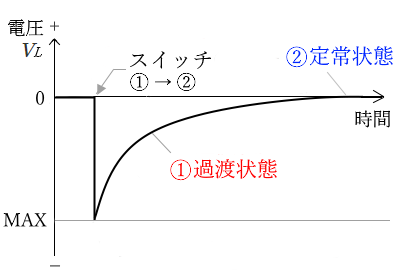
コイルにかかる電圧 $V_L$ のグラフ
① フルに充電された状態のコイルの電圧 $V_L$ は、電源と逆向きの電圧になります。これを放電させますので、徐々に電圧は低下していきます。
② コイルが完全に放電されると、電圧は 0 になります。
時定数と仮想短絡・仮想開放
コンデンサやコイルが接続された直流回路に電流を流しはじめてから、定常状態になるまでの電流の変化の速さを表す定数を「時定数」といいます。時定数 $T$ を表す式は次のようになります。
$R$ – $C$ 回路における時定数の公式
$T=CR$
$T$[秒]:時定数
$C$[F]:静電容量
$R$[Ω]:抵抗
$R$ – $L$ 回路における時定数の公式
$T=\displaystyle\frac{L}{R}$
$T$[秒]:時定数
$L$[H]:インダクタンス
$R$[Ω]:抵抗
時定数が小さければ、早く定常状態に近づきますが、時定数が大きければ、ゆるやかに定常状態に近づきます。
コンデンサの仮想短絡と仮想開放

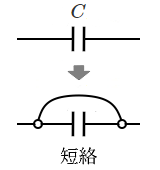
図のようにコンデンサ、抵抗と直流電源を直列に接続した回路において、スイッチを入れた瞬間のコンデンサは、電流の流れを妨げることなく、100% の電流が流れます。つまり、スイッチを入れた瞬間のコンデンサは「仮想短絡状態」といえます。
また、100% 充電された定常状態のコンデンサには、電流は流れません。つまり、定常状態のコンデンサは「仮想開放状態」といえます。
スイッチを入れた瞬間のコンデンサ:仮想短絡状態
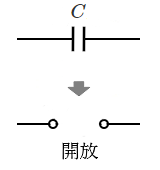
定常状態のコンデンサ:仮想開放状態
コイルの仮想短絡と仮想開放


図のようにコイル、抵抗と直流電源を直列に接続した回路において、スイッチを入れた瞬間のコイルは、自己誘導により電流の流れを妨げるため、電流が流れません。つまり、スイッチを入れた瞬間のコンデンサは「仮想開放状態」といえます。
また、100% 充電された定常状態のコイルは、自己誘導による逆起電力は発生せず、抵抗は 0 になります。つまり、定常状態のコンデンサは「仮想短絡状態」といえます。
スイッチを入れた瞬間のコイル:仮想開放状態
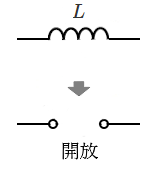
定常状態のコイル:仮想短絡状態
過渡現象の問題を解くポイント
電験三種の試験では、過渡現象の問題がほぼ毎年出題されています。過渡現象を計算式で解くには、微積分やラプラス変換といった、高度な数学知識が必要になります。ただし、電験三種では難しい微分方程式を使わなくても、「どのような現象が起こっているのか」ということと、時定数の公式を覚えておけば、ほとんどの問題が解けてしまいます。ここでは、「どのような現象が起こっているのか」について、簡単に説明をします。
抵抗について
理想的な抵抗は、電圧や電流の時間変化とは関係がない式(オームの法則)で表されます。したがって、抵抗 $R$ は、如何なる状況であっても抵抗 $R$ として扱います。
コンデンサについて
コンデンサは、二つの電極が向かい合ったものです。この電極間に電流が流れ込むと、蓄積された電荷の量に比例した電圧が発生します。抵抗が直列に接続されている場合は、コンデンサの端子電圧が印加電圧と同じになるまでに時間を要します。これは、ある速度で電荷が蓄積されていくからです。
一方で、抵抗の無いコンデンサだけの回路の場合は、所要時間 0 でコンデンサの端子電圧と印加電圧は同じになります。これは、無限の速度で電荷が蓄積されることを意味します。見方を変えると、電荷がコンデンサの方へ、無限の速度で移動するということになります。これは、抵抗分が全くなく、0 であるためです。
したがって、スイッチを入れた瞬間や、切った瞬間といった過渡現象中のコンデンサは、短絡 (short) と同じであると想定することができます。また、十分に時間が経過した後の定常状態中のコンデンサは、時間変化の無い直流状態ですから、コンデンサは単なる離れた電極となります。つまり、開放 (open) として扱うことができます。
印加電圧の考え方ですが、コンデンサの端子電圧より印加電圧が高い場合はコンデンサは充電し、端子電圧より低い場合(0Vも含む)はコンデンサは放電をします。この充放電を行っている間が、過渡現象です。コンデンサの端子電圧と印加電圧が同じになると、コンデンサは充放電をやめ、定常状態になります。
コイルについて
コイルの電流と電圧の特性は、電流の変化に対する逆起電力が元となっています。電流変化が大きいほど、逆起電力が大きくなり、電流変化がなくなれば、逆起電力は発生しません。
したがって、スイッチを入れた瞬間や、スイッチを切った瞬間は、極めて大きな電流変化が伴いますので、大きな逆起電力が発生します。これを、究極の場合で考えると、その逆起電力によってコイルには電流が流れなくなり、開放 (open) と同じであると想定することができます。過渡現象中のコイルは、開放 (open)状態として扱うことができます。
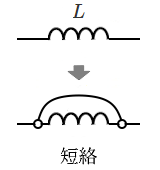
一方で、十分に時間が経過した後は,時間変化の無い直流状態ですから、コイルは単なる導線と同じになります。定常状態中のコイルは短絡 (short) として扱うことができます。
印加電圧の考え方ですが、コイルの端子電圧より印加電圧が高い場合はコイルはエネルギーを蓄積し、端子電圧より低い場合(0Vも含む)はコイルはエネルギーを放出します。この蓄積・放出を行っている間が、過渡現象です。コイルの端子電圧と印加電圧が同じになると、コイルは蓄積・放出をやめ、定常状態になります。
電験三種-理論の過去問解説:過渡現象
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2001年(平成13年)問5【電験理論の過去問題】
図の回路において、スイッチSを閉じた瞬間(時刻 $t=0$)に抵抗 $R_1$ に流れる電流を $I_0$ [A] とする。また、スイッチSを閉じた後、回路が定常状態に達したとき、同じ抵抗 $R_1$ に流れる電流 $I_∞$ [A] とする。
上記の電流 $I_0$ 及び $I_∞$ の値の組み合わせとして、正しいのは次のうちどれか。
ただし、コンデンサ $C$ の初期電荷は零とする。
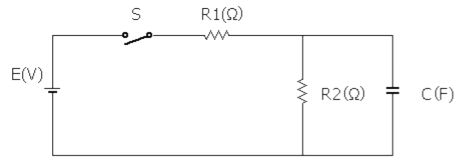
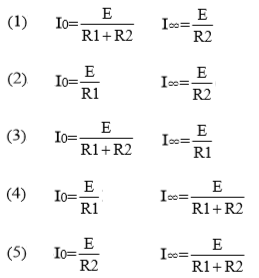
スイッチSを閉じた瞬間(時刻 $t=0$)、コンデンサーは過渡現象により、充電をはじめます。過渡現象中のコンデンサーは短絡状態になりますので、電流は $R_2$ には流れません。したがって、
$I_0=\displaystyle\frac{E}{R_1}$
定常状態になると、コンデンサーは充電が終わり開放状態になりますので、電流は $R_1$ と $R_2$ に流れます。したがって、
$I_∞=\displaystyle\frac{E}{R_1+R_2}$
答え (4)
2002年(平成14年)問9【電験理論の過去問題】
図の回路において、スイッチSが開いているとき、静電容量 $C_1=0.004$ [F] のコンデンサには電荷 $Q_1=0.3$ [C] が蓄積されており、静電容量 $C_2=0.002$ [F] のコンデンサの電荷は $Q_2=0$ [C] である。この状態でスイッチSを閉じて、それから時間が十分に経過して過渡現象が終了した。この間に抵抗 $R$ [Ω] で消費された電気エネルギー [J] の値として、正しいのは次のうちどれか。
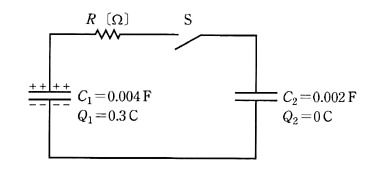
(1) 2.50 (2) 3.75 (3) 7.50 (4) 11.25 (5) 13.33
コンデンサ $C_1=0.004$ [F] に蓄えられた静電エネルギーを $W_1$ [J] とすると、
$W_1=\displaystyle\frac{1}{2}C_1V_1^2=\displaystyle\frac{1}{2}C_1\left(\displaystyle\frac{Q_1}{C_1}\right)^2=\displaystyle\frac{1}{2}×\displaystyle\frac{0.3^2}{0.004}=11.25$ [J]
スイッチSを閉じたときの全電荷 $Q$ は $Q=0.3$ [C] で、全静電容量 $C$ は $C=0.004+0.002=0.006$ [F] ですので、全静電エネルギーを $W_2$ [J] とすると、
$W_2=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{1}{2}C\left(\displaystyle\frac{Q}{C}\right)^2=\displaystyle\frac{1}{2}×\displaystyle\frac{0.3^2}{0.006}=7.5$ [J]
この間に抵抗 $R$ [Ω] で消費された電気エネルギー $W$ [J] は、
$W=W_1-W_2=11.25-7.5=3.75$ [J]
答え (2)
2003年(平成15年)問9【電験理論の過去問題】
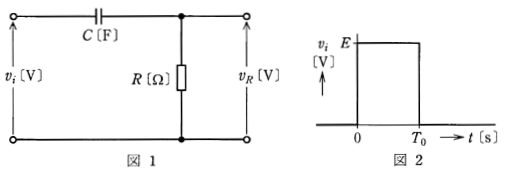
図1のような静電容量 $C$ [F] のコンデンサと抵抗 $R$ [Ω] の直列回路に、図2のような振幅 $E$ [V] 、パルス幅 $T_0$ [s] の方形波電圧 $v_i$ [V] を加えた。このときの抵抗 $R$ の端子間電圧 $v_R$ [V]の波形として、正しいのは次のうちどれか。
ただし、図1の回路の時定数 $RC$ [s]は $T_0$ [s] より十分小さく( $RC≪T_0$ )、電源の内部インピーダンス及びコンデンサの初期電荷は零とする。
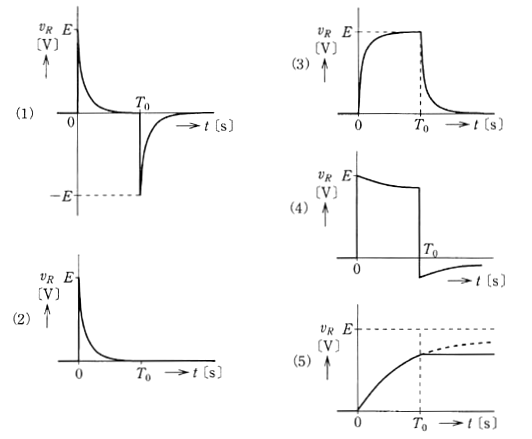
パルス電圧が印加される(時刻 $t=0$ のとき)とコンデンサーは充電を開始します。パルス電圧がなくなる(時刻 $t=T_0$ のとき)コンデンサーは放電を始めます。
- 電圧が加わった瞬間はコンデンサは導通状態ですので、抵抗には $E$ [V] の電圧が加わります。
- 電圧が加わった瞬間から $T_0$ [s] までコンデンサは充電を続けます。このとき $v_R$ [V] は、ゼロに近づいていきます。
- 時刻 $t=T_0$ で、充電が終わり、放電を行います。このとき、蓄えられた電圧が放電されます。抵抗には $-E$ [V] の電圧が加わります。
- 放電電圧は時間の経過とともに、ゼロに近づいていきます。
答え (1)
2004年(平成16年)問9【電験理論の過去問題】
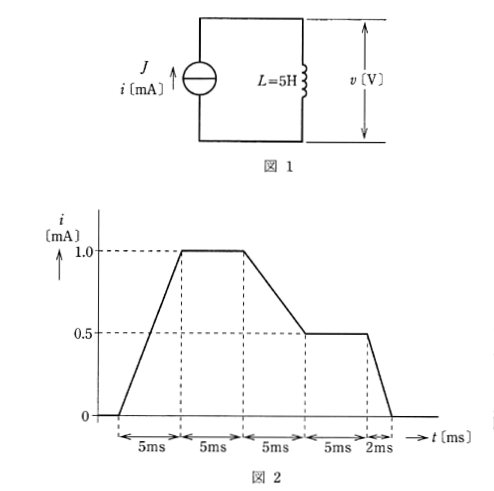
図1のように、インダクタンスクタンス $L=5$ [H] のコイルに直流電流源 $J$ が電流 $i$ [mA] を供給している回路がある。電流 $i$ [mA] は図2のような時間変化をしている。このとき、コイルの端子間に現れる電圧の大きさ $|v|$ [V] の最大値として、正しいのは次のうちどれか。
(1) 0.25 (2) 0.5 (3) 1 (4) 1.25 (5) 1.5
コイルの端子間に現れる電圧の大きさ $|v|$ [V] は、 $|v|=L\displaystyle\frac{di}{dt}$ ですので、単位時間中に電流の変化が最も大きな場合に、最も大きな電圧が誘起されます。したがって、2 [ms] で 0.5 [mA] の変化がある箇所が該当します。
$|v|=L\displaystyle\frac{di}{dt}=5×\displaystyle\frac{0.5×10^{-3}}{2×10^{-3}}=1.25$ [V]
答え (4)
2005年(平成17年)問9【電験理論の過去問題】
図のように、抵抗 $R$ とインダクタンス $L$ のコイルを直列に接続した回路がある。この回路において、スイッチSを時刻 $t=0$ で閉じた場合に流れる電流及び各素子の端子間電圧に関する記述として、誤っているのは次のうちどれか。
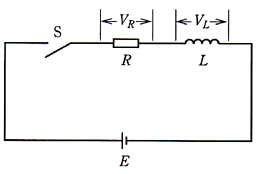
- この回路の時定数は、$L$ の値に比例している。
- $R$ の値を大きくするとこの回路の時定数は、小さくなる。
- スイッチSを閉じた瞬間(時刻 $t=0$)のコイルの端子間電圧 $V_L$ の大きさは、零である。
- 定常状態の電流は、$L$ の値に関係しない。
- 抵抗 $R$ の端子間電圧 $V_R$ の大きさは、定常状態では電源電圧 $E$ の大きさに等しくなる。
題意の回路の過渡現象中にコイルに流れる電流 $I$ [A] は、
$I=\displaystyle\frac{V_0}{R}(1-e^{-\frac{Rt}{L}})$
時定数 $τ$ は、
$τ=\displaystyle\frac{L}{R}$[s]
$L$ が大きく、$R$ が小さいほど、過渡現象は長く続きます。定常時とは、$t$ が大きいことですので、コイルに流れる電流は0に近づいていくことになります。つまり、定常時の電流は、$L$ の値に関係しません。また、スイッチSを閉じた瞬間(時刻 $t=0$)のコイルの端子間電圧 $V_L$ の大きさは、最大になります。したがって、(3)の記述が誤りです。
答え (3)
2006年(平成18年)問10【電験理論の過去問題】
図のような回路において、スイッチSを①側に閉じて、回路が定常状態に達した後で、スイッチSを切り換え②側に閉じた。スイッチS、抵抗 $R_2$ 及びコンデンサ $C$ からなる閉回路の時定数の値として、正しいのは次のうちどれか。
ただし、抵抗 $R_1=300$ [Ω] 、抵抗 $R_2=100$ [Ω] 、コンデンサ $C$ の静電容量 $=20$ [μF] 、直流電圧 $E=10$ [V] とする。
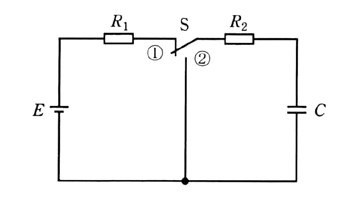
(1) 0.05[μs] (2) 0.2[μs] (3) 1.5[ms] (4) 2.0[ms] (5) 8.0[ms]
スイッチSを切り換え②側に閉じたときの、時定数は $τ=R_2C$[s]ですので、
$τ=R_2C=100×10×10^{-6}=2×10^{-3}$[s]
答え (4)
2007年(平成19年)問10【電験理論の過去問題】
図1から図5に示す5種類の回路は、$R$ [Ω] の抵抗と静電容量 $C$ [F] のコンデンサの個数と組み合わせを異にしたものである。コンデンサの初期電荷を零として、スイッチSを閉じたときの回路の過渡的な現象を考える。そのとき、これら回路のうちで時定数が最も大きい回路を示す図として、正しいのは次のうちどれか。
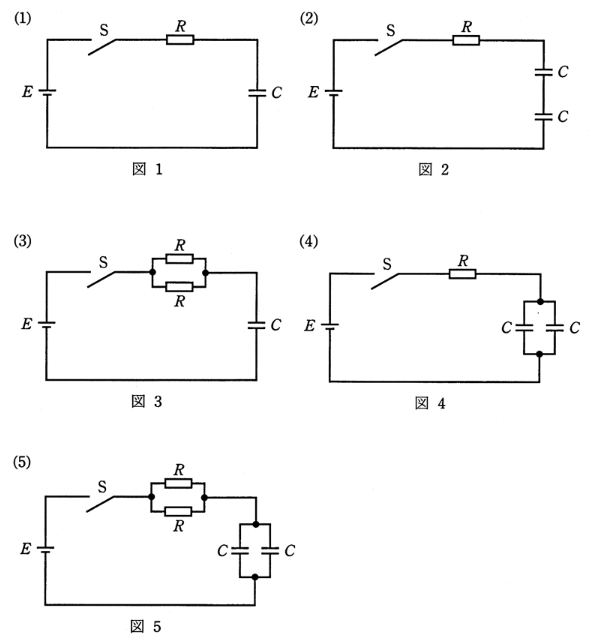
時定数は $τ=RC$[s]で表すことができます。各回路の合成抵抗と合成静電容量から導きます。
図1:$τ=RC$
図2:$τ=R×\displaystyle\frac{C}{2}=\displaystyle\frac{1}{2}RC$
図3:$τ=\displaystyle\frac{R}{2}×C=\displaystyle\frac{1}{2}RC$
図4:$τ=R×2C=2RC$
図5:$τ=\displaystyle\frac{R}{2}×2C=RC$
したがって、(4)が一番大きくなります。
答え (4)
2008年(平成20年)問10【電験理論の過去問題】
図のように、開いた状態のスイッチS、$R$ [Ω] の抵抗、インダクタンス $L$ [H] のコイル、直流電源 $E$ [V] からなる直流回路がある。この直流回路において、スイッチSを閉じた直後に過渡現象が起こる。この場合に、「回路に流れる電流」、「抵抗の端子電圧」、及び「コイルの端子電圧」に関し、時間の経過にしたがって起こる過渡現象として、正しいものを組み合わせたのは次のうちどれか。
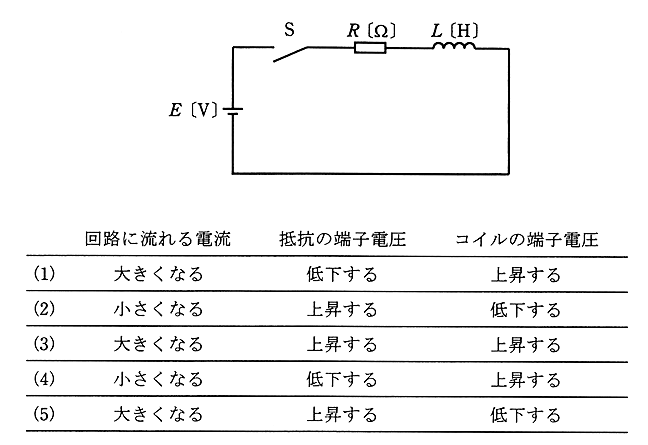
RL回路の過渡現象は、回路に流れる電流は時間の経過とともに大きくなり、抵抗の端子電圧は上昇し最終的には電源電圧と等しくなります。コイルの端子電圧は低下し最終的には零になります。
答え (5)
2009年(平成21年)問10【電験理論の過去問題】
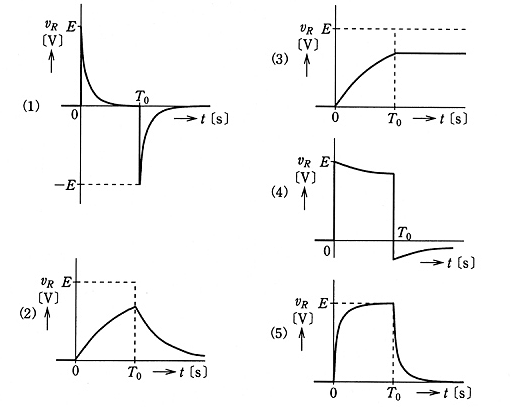
図1のようなインダクタンス $L$ [H] のコイルと $R$ [Ω] の抵抗からなる直列回路に、図2のような振幅 $E$ [V] 、パルス幅 $T_0$ [s] の方形波電圧 $v_i$ [V] を加えた。このときの抵抗 $R$ [Ω] の端子間電圧 $v_R$ [V] の波形を示す図として、正しいのは次のうちどれか。
ただし、図1の回路の時定数 $\displaystyle\frac{L}{R}$ [s]は $T_0$ [s]より十分小さく( $\displaystyle\frac{L}{R}≪T_0$ )、方形波電圧 $v_i$ [V] を発生する電源の内部インピーダンスは $0$ [Ω] とし、コイルに流れる初期電流は $0$ [A] とする。
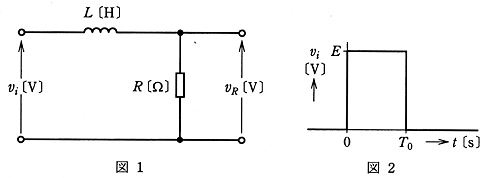
コイルに電流を流し始めた時のRL回路の過渡現象では、コイルに流れる電流 $I$ [A] は、
$I=\displaystyle\frac{E}{R}(1-e^{-\frac{Rt}{L}})$
コイルに流れている電流を遮断した時のRL回路の過渡現象では、コイルに流れる電流 $I$ [A] は、
$I=\displaystyle\frac{E}{R}e^{-\frac{Rt}{L}}$
方形波電圧 $v_i$ [V] が印加されたとき、抵抗 $R$ [Ω]の端子間電圧 $v_R$ [V] は、
$v_R=IR=E(1-e^{-\frac{Rt}{L}})$
で表すことができます。時定数 $\displaystyle\frac{L}{R}$ [s] は $T_0$ [s] より十分小さい( $\displaystyle\frac{L}{R}≪T_0$ )ので、端子間電圧 $v_R$ [V] は、急速に 0 から $E$ [V] になります。
また、方形波電圧 $v_i$ [V] がなくなったとき、抵抗 $R$ [Ω] の端子間電圧 $v_R$ [V] は、
$v_R=IR=Ee^{-\frac{Rt}{L}}$
で表すことができます。端子間電圧 $v_R$ [V] は、急速に $E$ から 0 [V] になります。したがって、合致する波形は(5)です。
答え (5)
2010年(平成22年)問10【電験理論の過去問題】
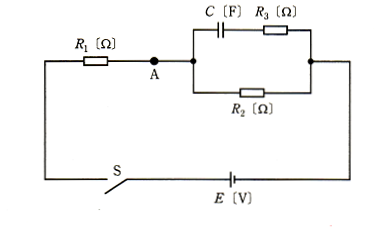
図に示す回路において、スイッチSを閉じた瞬間(時刻 $t=0$ )に点Aを流れる電流を $I_0$ [A] とし、十分に時間が経ち、定常状態に達したのちに点Aを流れる電流を $I$ [A]とする。電流比 $\displaystyle\frac{I_0}{I}$ の値を2とするために必要な抵抗 $R_3$ [Ω] の値を表す式として、正しいのは次のうちどれか。
ただし、コンデンサの初期電荷は零とする。
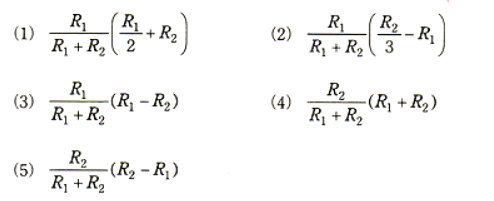
過渡現象中のコンデンサ $C$ は、短絡状態になりますので、点Aを流れる電流 $I_0$ [A] は、
$I_0=\displaystyle\frac{E}{R_1+\displaystyle\frac{R_2R_3}{R_2+R_3}}=\displaystyle\frac{(R_2+R_3)E}{R_1(R_2+R_3)+R_2R_3}$ [A]
定常状態に達したのちのコンデンサ $C$ は、開放状態になりますので、点Aを流れる電流 $I$ [A] は、
$I=\displaystyle\frac{E}{R_1+R_2}$
$\displaystyle\frac{I_0}{I}=2$ なので、
$\displaystyle\frac{(R_2+R_3)(R_1+R_2)}{R_1(R_2+R_3)+R_2R_3}=2$
$R_3(R_1+R_2)=R_2(R_2-R_1)$
$R_3=\displaystyle\frac{R_2}{R_1+R_2}(R_2-R_1)$
答え (5)
2011年(平成23年)問10【電験理論の過去問題】
図のように、2種類の直流電源、$R$ [Ω] の抵抗、静電容量 $C$ [F] のコンデンサ及びスイッチSからなる回路がある。この回路において、スイッチSを①側に閉じて回路が定常状態に達した後に、時刻 $t=0$ [s] でスイッチSを①側から②側に切り換えた。②側への切り換え以降の、コンデンサから流れ出る電流 $i$ [A] の時間変化を示す図として、正しいものを次の(1)~(5)のうちから一つ選べ。
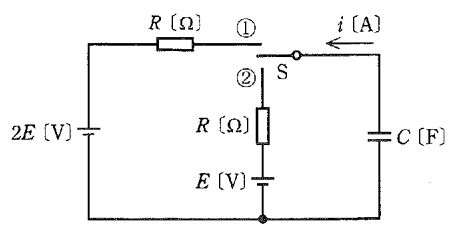
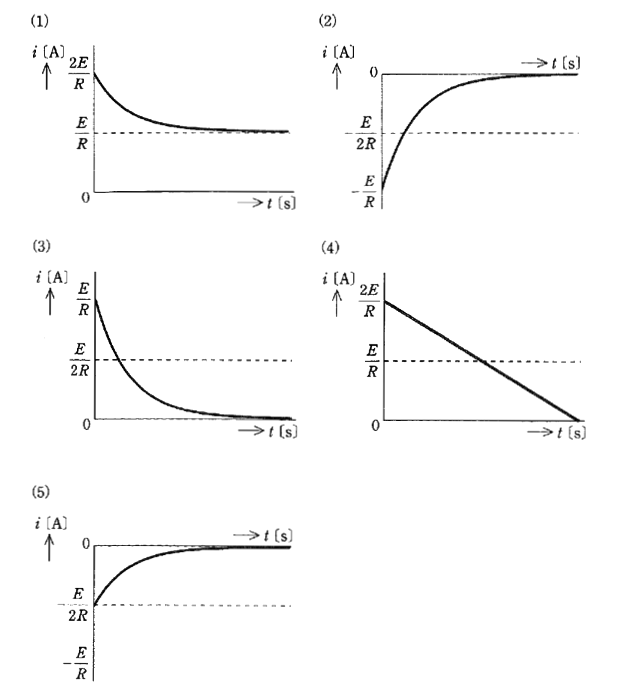
スイッチSを①側に閉じているときコンデンサは電圧 $2E$ [V] で、充電されています。スイッチを②側への切り換えた瞬間は、電源は $E$ [V] ですので、コンデンサと電源間に電位差が生じて、電流 $i=\displaystyle\frac{E}{R}$ が流れます。
その後、電流は減少していき、コンデンサ電圧と電源電圧が等しくなったところで零になります。
答え (3)
2012年(平成24年)問9【電験理論の過去問題】
図のように、直流電圧 $E$ [V] の電源、$R$ [Ω] の抵抗、インダクタンス $L$ [H] のコイル、スイッチS1とS2からなる回路がある。電源の内部インピーダンスは零とする。時刻 $t=t_1$ [s] でスイッチS1を閉じ、その後、時定数 $\displaystyle\frac{L}{R}$ [s] に比べて十分に時間が経過した時刻 $t=t_2$ [s] でスイッチS2を閉じる。このとき、電源から流れ出る電流 $i$ [A] の波形を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
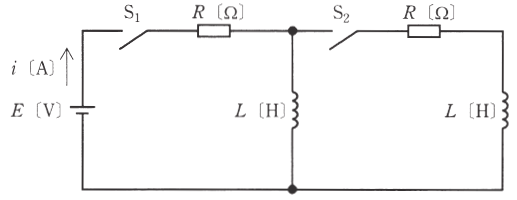
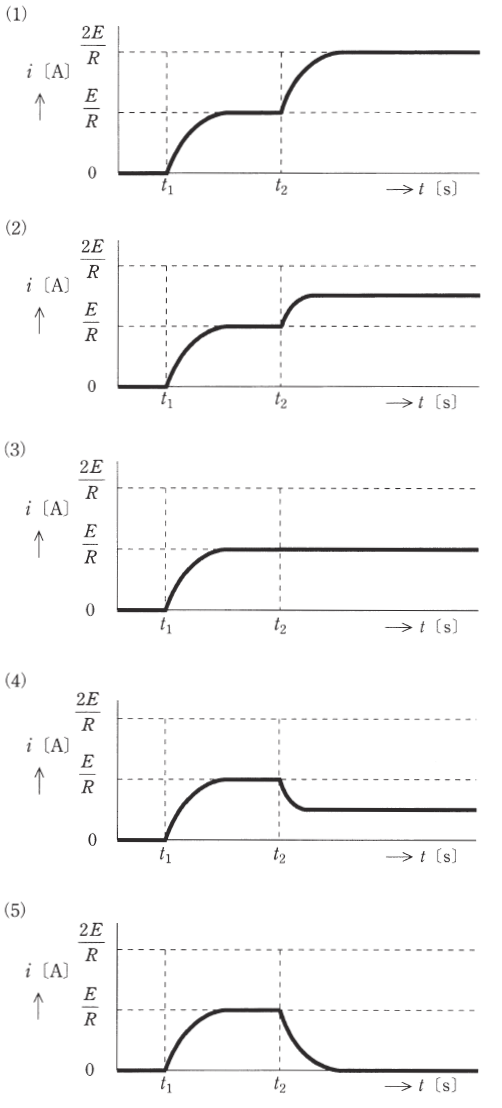
時刻 $t=t_1$ [s] でスイッチS1を閉じると過渡現象で電流が流れます。電流は $i=\displaystyle\frac{E}{R}$ で一定となります。
定常状態になるとコイルは短絡状態になりますので、スイッチS2を閉じてもS2側には電流は流れません。$i=\displaystyle\frac{E}{R}$ で一定を保ち続けます。
答え (3)
電験三種 過去問解説 2013年(平成25年)問12
図の回路において、十分に長い時間開いていたスイッチSを時刻 $t=0$[ms]から時刻 $t=15$[ms]の間だけ閉じた。このとき、インダクタンス $20$[mH]のコイルの端子間電圧 $v$[V]の時間変化を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
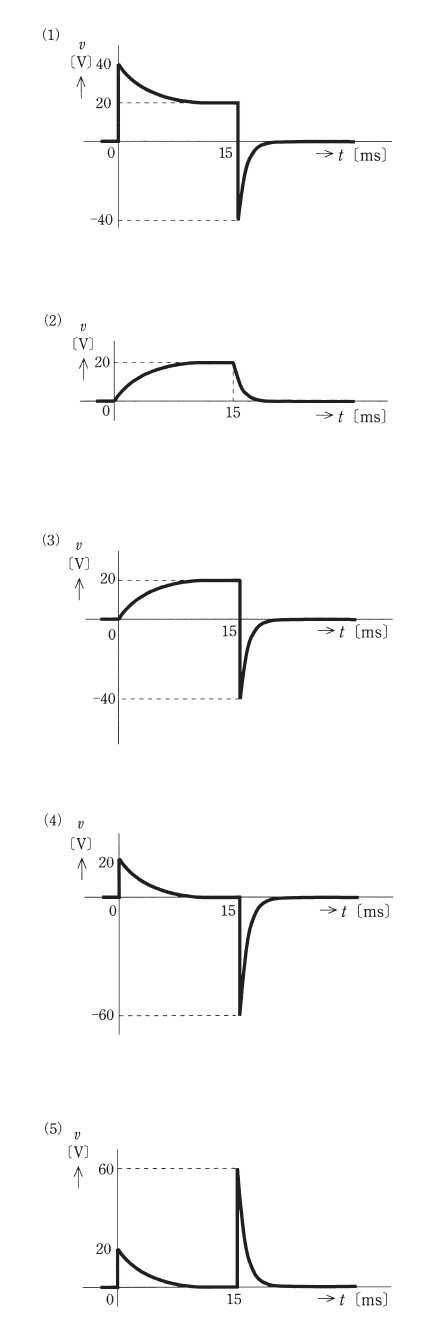
スイッチを閉じた瞬間( $t=0$[ms])は、コイルに逆起電力が発生するのでコイルには電流が流れません。コイルの端子間電圧 $v$[V]は 20 [Ω] の抵抗にかかる電圧と同じになります
$v=30×\displaystyle\frac{20}{10+20}=20$[V]
t=0[ms]から t=15[ms]の間は、時間の経過とともにコイルに電流が流れます。コイルに流れる電流は、$I=\displaystyle\frac{V_0}{R}(1-e^{-\frac{Rt}{L}})$ [A] です。最終的には、コイルは短絡状態になります。コイルの端子間電圧 $v$[V]は 0 [V] になったとき(定常状態時)に、コイルに流れる電流は、
$I=\displaystyle\frac{V_0}{R}(1-0)=\displaystyle\frac{30}{10}=3$ [A]
となり、この電流のエネルギーをコイルは蓄えます。
スイッチを開いた瞬間( $t=15$[ms])は、コイルに蓄えられたエネルギーを放出します。コイルが蓄えた電流は、 3 [A] でした。 これを、20[Ω]の抵抗を通じて放電するので、コイルの端子間電圧 $v$[V]は 60[V]になります。このときコイルには逆方向に電流が流れますので、コイルに発生する起電力の方向は逆方向なります。そして、コイルはエネルギーを放出しながら、最終的には 0 [V] になります。
答え (4)
2014年(平成26年)問11【電験理論の過去問題】
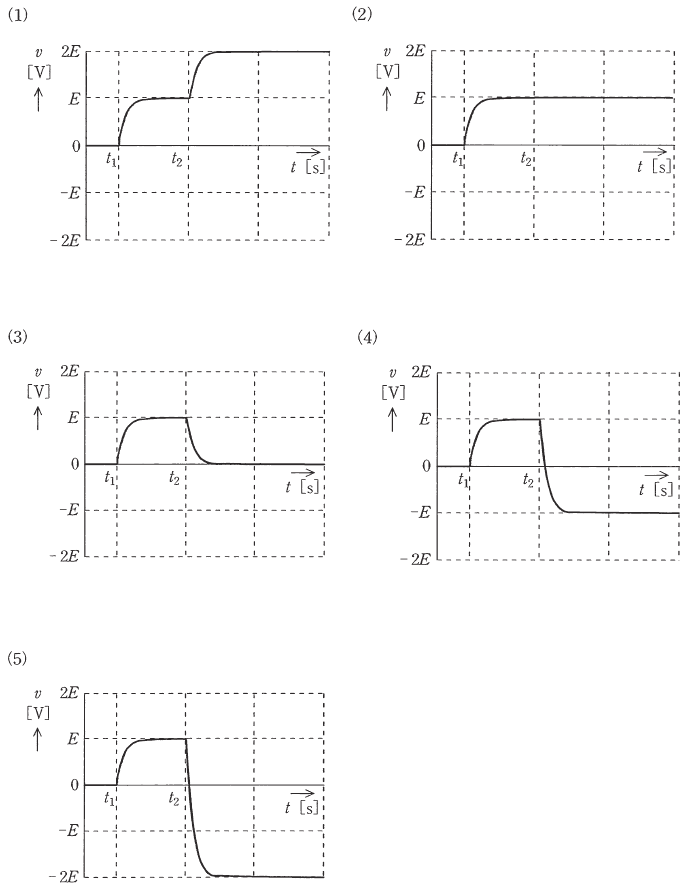
図のように、直流電圧 $E$ [V] の電源が2個、$R$ [Ω] の抵抗が2個、静電容量 $C$ [F] のコンデンサ、スイッチS1とS2からなる回路がある。スイッチS1とS2の初期状態は、共に開いているものとする。電源の内部インピーダンスは零とする。時刻 $t=t_1$ [s] でスイッチS1を閉じ、その後、時定数 $CR$ [s] に比べて十分に時間が経過した時刻 $t=t_2$ [s] でスイッチS1を開き、スイッチS2を閉じる。このとき、コンデンサの端子電圧 $v$ [V] の波形を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの初期電荷は零とする。
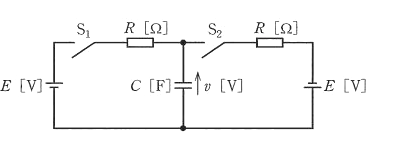
時刻 $t=t_1$ [s] でスイッチS1を閉じたとき、コンデンサーは左側の電源電圧 $E$ [V] で、充電されていきます。コンデンサーの端子電圧 $v$ [V] と電源電圧 $E$ [V] が等しくなると充電が終わり、定常状態になります。
時刻 $t=t_2$ [s] でスイッチS1を開き、スイッチS2を閉じると、右側の電源電圧と接続されることになります。右側の電源電圧は、左側の電源電圧と逆向きなので、コンデンサは放電しながら端子電圧を下げていき、0 [V] を通り越すと、右側の電源電圧 $E$ [V] によって、マイナス側に充電されていきます。そして、コンデンサーの端子電圧 $v$ [V]と電源電圧 $E$ [V] が等しくなると充電が終わり、定常状態になります。
答え (4)
2015年(平成27年)問10【電験理論の過去問題】
図のように、直流電圧 $E$ [V] の電源、抵抗 $R$ [Ω] の抵抗器、インダクタンス $L$ [H] のコイルまたは静電容量 $C$ [F] のコンデンサ、スイッチSからなる2種類の回路( RL回路、RC回路 )がある。各回路において、時刻 $t=0$ s でスイッチSを閉じたとき、回路を流れる電流 $i$ [A] 、抵抗の端子電圧 $v_r$ [V] 、コイルの端子電圧 $v_l$ [V] 、コンデンサの端子電圧 $v_c$ [V] の波形の組合せを示す図として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、電源の内部インピーダンス及びコンデンサの初期電荷は零とする。
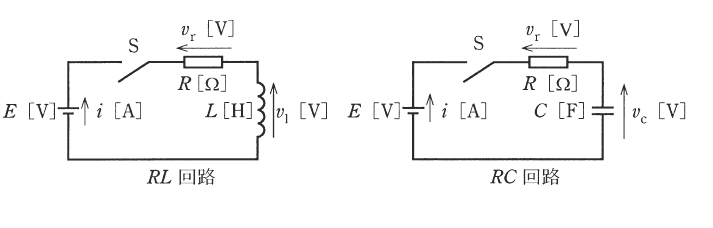
コンデンサーに充電する時の過渡現象とコイルに電流を流し始めた時の過渡現象を参照してください。
答え (2)
2016年(平成28年)問10【電験理論の過去問題】
図のように、電圧 $E$ [V] の直流電源、スイッチS、$R$ [Ω] の抵抗及び静電容量 $C$ [F] のコンデンサからなる回路がある。この回路において、スイッチSを1側に接続してコンデンサを十分に充電した後、時刻 $t=0$ s で、スイッチSを1側から2側に切り換えた。2側に切り換えた以降の記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、自然対数の底は、2.718とする。
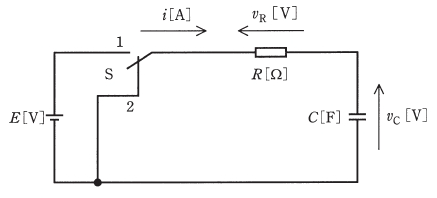
- 回路の時定数は、$C$ の値 [F] に比例する。
- コンデンサの端子電圧 $v_c$ [V] は、$R$ の値 [Ω] が大きいほど緩やかに減少する。
- 時刻 $t=0$ s から回路の時定数だけ時間が経過すると、コンデンサの端子電圧 $v_c$ [V] は直流電源の電圧 $E$ [V] の0.368倍に減少する。
- 抵抗の端子電圧 $V_R$ [V] の極性は、切り換え前(コンデンサ充電中)と逆になる。
- 時刻 $t=0$ s における回路の電流 $i$ [A] は、$C$ の値 [F] に関係する。
題意の回路の過渡現象中にコンデンサーに流れる電流 $I$、コンデンサー電圧 $V$、時定数 $τ$は、次の通りです。
$I=-\displaystyle\frac{dQ}{dt}=\displaystyle\frac{Q_0}{RC}e^{-\frac{t}{RC}}=I_0e^{-\frac{t}{RC}}$
$V=\displaystyle\frac{Q}{C}=\displaystyle\frac{CV_0}{C}e^{-\frac{t}{RC}}=V_0e^{-\frac{t}{RC}}$
$τ=RC$[s]
(5)の記述で、時刻 $t=0$ s のときは、回路の電流 $i$ [A] はコンデンサが蓄えた電圧 $E$ [V] と抵抗 $R$ [Ω] の値で決まります。したがって、(5)の記述が誤りです。
答え (5)
2017年(平成29年)問10【電験理論の過去問題】
図のように、電圧 $E$ [V]の直流電源に、開いた状態のスイッチ $S$,$R_1$[Ω]の抵抗,$R_2$[Ω]の抵抗及び電流が $0A$ のコイル(インダクタンス $L$[H])を接続した回路がある。次の文章は、この回路に関する記述である。
1 スイッチSを閉じた瞬間(時刻 $t=0s$ )に $R_1$[Ω]の抵抗に流れる電流は、( ア )[A]となる。
2 スイッチSを閉じて回路が定常状態とみなせるとき、$R_1$[Ω]の抵抗に流れる電流は、( イ )[A]となる。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
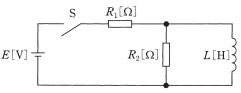

スイッチSを閉じた瞬間(時刻 $t=0s$ )は、コイルに逆起電力が発生するのでコイルには電流が流れません。つまり、コイルは開放状態と考えることができますので、$R_1$[Ω]の抵抗に流れる電流 $I_1$[A]は、
$I_1=\displaystyle\frac{E}{R_1+R_2}$
スイッチSを閉じて回路が定常状態とみなせるとき、時間変化の無い直流状態ですから、コイルは単なる導線と同じになります。定常状態中のコイルは短絡状態として扱うことができますので、$R_1$[Ω]の抵抗に流れる電流 $I_2$[A]は、
$I_1=\displaystyle\frac{E}{R_1}$
答え(1)
電験三種の理論科目に出題される「電気電子工学(電気の現象)」のページ
1.電気の単位と抵抗温度係数
2.電界中の電子の運動
3.ローレンツ力の向きと円運動
4.電子放出と熱起電力の原理
5.過渡現象と時定数とは






