このページでは、直流機の定格について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目で、実際に出題された直流機の定格の過去問題の解き方も解説しています。
直流発電機の定格
図のように直流発電機Gを原動機で回転させると、起電力が発生し、スイッチSを閉じると、発電機は負荷に電力 $P_o$[W]を供給します。 この場合、発電機は回転速度 $n$[min-1]がいくらで、電圧 $V$[V]がいくらのもとで、どの程度の電流 $I$[A]を取り出せるかがわかっていなければ、発電機が過熱したり、焼損したりするおそれがあります。
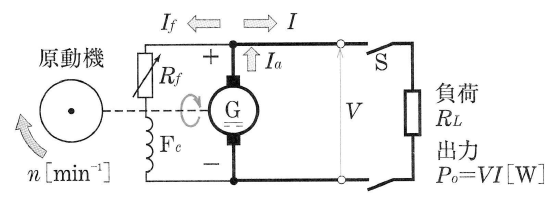
そこで、発電機には、電圧・電流・出力・回転速度、および連続的に使用するか、間欠的に使用するかなどについて、標準的な使い方を示す値が銘板に示されています。これらの値を発電機の定格または定格値といいます。定格電圧で定格電流が流れる負荷を定格負荷といいます。
電圧変動率
原動機が定格回転速度 $n_n$[min-1]で回転しているとき、負荷電流 $I$[A]を 増加させると、電機子反作用による電圧降下などのため端子電圧 $V$[V]は低下します。その程度を表すのに電圧変動率を用います。無負荷のときの電圧を $V_o$[V]、 定格負荷のときの電圧を $V_n$[V]とすると、電圧変動率 $ε$[%]は、次の式で表すことができます。
電圧変動率を求める式
$ε=\displaystyle\frac{V_o-V_n}{V_n}×100$
$ε$[%]:電圧変動率
$V_o$[V]:無負荷のときの電圧
$V_n$[V]:定格負荷のときの電圧
効率
直流発電機の電機子は、負荷電流が流れると、原動機の回転の向きと逆向きに力を受けます。この力に打ち勝って、電機子を回転速度 $n$[min-1]で回転させるのに必要な動力 $P_i$[W]は、電動機の機械動力に変換される電力 $P_i=EI_a$ で表されます。
ところで、外部負荷に供給される電力、つまり $P_o$[W]は、$P_o=VI$ です。一般に $P_o$ は $P_i$ より小さくなります。その差 $P_i-P_o=P_l$ は発電機の損失となります。そこで、発電機の効率 $η$[%]は、次の式で表すことができます。
発電機の効率を求める式
$η=\displaystyle\frac{P_o}{P_i}×100=\displaystyle\frac{P_o}{P_o+P_l}×100$
$η$[%]:発電機の効率
$P_o$[W]:発電機出力
$P_i$[W]:発電機入力
$P_l$[W]:発電機損失
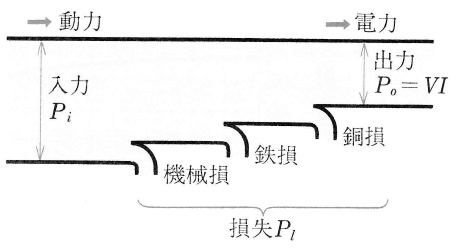
発電機の損失には、電機子巻線や界磁巻線による抵抗損とブラシ接触抵抗による抵抗損からなる銅損、鉄心中の損失、つまり渦電流損やヒステリシス損からなる鉄損、回転子の運動による軸受の摩擦損などの機械損などがあります。
直流電動機の定格
図に示すように、直流電動機に機械的な負荷を結合して運転するとき、負荷が大きすぎると負荷電流が定格電流以上になり、電機子巻線を焼損するおそれがあります。直流電動機にも、その銘板に定格が示されているので、それに従って使用しなければなりません。
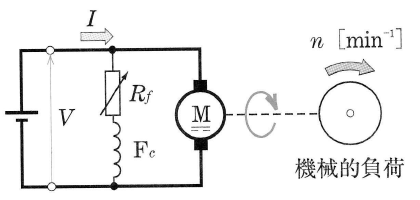
速度変動率
負荷を増加すると、回転速度は一般に低下します。その程度を表すのに速度変動率を用います。無負荷のときの回転速度を $n_o$[min-1]とし、定格負荷のときの回転速度を $n_n$[min-1]とすると、速度変動率 $δ$[%]は、次の式で表すことができます。
速度変動率を求める式
$δ=\displaystyle\frac{n_o-n_n}{n_n}×100$
$δ$[%]:速度変動率
$n_o$[min-1]:無負荷のときの回転速度
$n_n$[min-1]:定格負荷のときの回転速度
効率
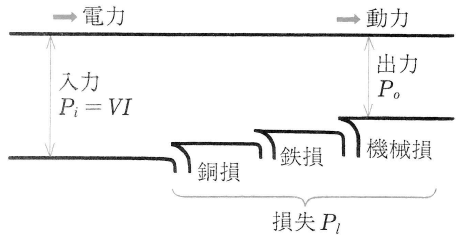
端子電圧 $V$[V]で、負荷電流 $I$[A]が流れると、電動機 には $P_i=VI$[W]の電力が供給されます。そのとき、電動機の機械的出力が $P_o$[W]、損失が $P_l$[W]とすれば、電動機の効率 $η$[%]は、次の式で表すことができます。
電動機の効率を求める式
$η=\displaystyle\frac{P_o}{P_i}×100=\displaystyle\frac{P_i-P_l}{P_i}×100$
$η$[%]:電動機の効率
$P_o$[W]:電動機出力
$P_i$[W]:電動機入力
$P_l$[W]:電動機損失
電験三種-機械(直流機)過去問
2004年(平成16年)問1
定格出力 2.2[kW]、定格回転速度 1500[min-1]、定格電圧 100[V]の直流分巻電動機がある。始動時の電機子電流を全負荷時の 1.5倍に抑えるための電機子巻線に直列に挿入すべき抵抗[Ω]の値として、最も近いのは次のうちどれか。
ただし、全負荷時の効率は 85[%]、電機子回路の抵抗は 0.15[Ω]、界磁電流は 2[A]とする。
(1) 2.43 (2) 2.58 (3) 2.64 (4) 2.79 (5) 3.18
2004年(平成16年)問1 過去問解説
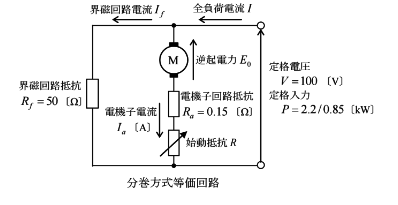
全負荷時の出力を $P$[W]、全負荷電流を $I$[A]、電動機の効率を $η$[%]とすると、
$P=VIη$
$I=\displaystyle\frac{P}{Vη}=\displaystyle\frac{2200}{100×0.85}=25.9$[A]
電機子電流 $I_a$[A]は、
$I_a=I-I_f=25.9-2=23.9$[A]
始動時の電機子電流を ${I_a}’$[A]とすると、
${I_a}’=1.5I_a=1.5×23.9=35.9$[A]
電機子巻線に直列に挿入すべき抵抗を $R$[Ω]は、
$R=\displaystyle\frac{V}{{I_a}’}-0.15=\displaystyle\frac{100}{35.9′}-0.15≒2.64$[Ω]
答え (3)
2006年(平成18年)問15
定格出力 100[kW]、定格電圧 220[V]の直流分巻発電機がある。この発電機の電機子巻線の抵抗は 0.05[Ω]、界磁巻線の抵抗は 57.5[Ω]、機械損の合計は 1.8[kW]である。この発電機を定格電圧、定格出力で運転しているとき、次の(a)及び(b)に答えよ。
ただし、ブラシによる電圧降下、補極巻線の抵抗、界磁鉄心と電機子鉄心の鉄損及び電機子反作用による電圧降下は無視できるものとする。
(a) この発電機の誘導起電力[V]の値として、最も近いのは次のうちどれか。
(1) 232 (2) 239 (3) 243 (4) 252 (5) 265
(b) この発電機の効率[%]の値として、最も近いものはどれか。
(1) 88 (2) 90 (3) 92 (4) 94 (5) 96
2006年(平成18年)問15 過去問解説
(a) 定格出力を $P$[W]、定格電圧を $V$[V]、定格電流を $I$[A]、誘導起電力を $E$[V]、電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]とすると、
$I=\displaystyle\frac{P}{V}=\displaystyle\frac{100×10^3}{220}=454.5$[A]
$I_f=\displaystyle\frac{V}{R_f}=\displaystyle\frac{220}{57.5}=3.83$[A]
$I_a=I-I_f=454.5-3.83=450.7$[A]
$E=V+R_aI_a=200+0.05×450.7=243$[V]
答え (3)
(b) 界磁損を $P_{ef}$[W]、電機子抵抗損を $P_{ea}$[W]とすると、
$P_{ef}={I_f}^2・R_f=3.83^2×57.5=843.5$[W]
$P_{ea}={I_a}^2・R_a=450.7^2×0.05=10156.5$[W]
損失の合計 $P_{e}$[W]は、
$P_{e}=1.8×10^3+10156.5+843.5=12800$[W]
発電機の効率 $η$[%]は、
$η=\displaystyle\frac{P_o}{P_i}×100$
$=\displaystyle\frac{100×10^3}{100×10^3+12800}×100≒88$[%]
答え (1)
2010年(平成22年)問2
直流発電機の損失は、固定損、直接負荷損、界磁回路損及び漂遊負荷損に分類される。
定格出力 50[kW]、定格電圧 200[V]の直流分巻発電機がある。この発電機の定格負荷時の効率は 94[%]である。このときの発電機の固定損[kW]の値として、最も近いのは次のうちどれか。
ただし、ブラシの電圧降下と漂遊負荷損は無視するものとする。また、電機子回路及び界磁回路の抵抗はそれぞれ 0.03[Ω]及び 200[Ω]とする。
(1) 1.10 (2) 1.12 (3) 1.13 (4) 1.30 (5) 1.32
2010年(平成22年)問2 過去問解説
定格出力を $P$[W]、端子電圧を $V$[V]、誘導起電力を $E$[V]、 負荷電流を $I$[A]、電機子電流を $I_a$[A]、電機子抵抗を $R_a$[Ω]、界磁電流を $I_f$[A]、界磁抵抗を $R_f$[Ω]とすると、
$I=\displaystyle\frac{P}{V}=\displaystyle\frac{50×10^3}{200}=250$[A]
$I_f=\displaystyle\frac{V}{R_f}=\displaystyle\frac{200}{200}=1$[A]
$I_a=I+I_f=250+1=251$[A]
定格負荷時の効率は 94[%]ですので、損失 $P_l$[W]は、
$94=\displaystyle\frac{50}{50+P_l}×100$
$P_l=\displaystyle\frac{50}{0.94}-50=3.19$[kW]
固定損 $P_r$[kW]は、
$P_r=P_l-R_a{I_a}^2-R_f{I_f}^2≒1.10$[kW]
答え (1)
2017年(平成29年)問1
界磁に永久磁石を用いた小形直流電動機があり、電源電圧は定格の 12V、回転を始める前の静止状態における始動電流は 4A、定格回転数における定格電流は 1Aである。定格運転時の効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ブラシの接触による電圧降下及び電機子反作用は無視できるものとし、損失は電機子巻線による銅損しか存在しないものとする。
(1) 60 (2) 65 (3) 70 (4) 75 (5) 80
2017年(平成29年)問1 過去問解説
端子電圧を $V$[V]、誘導起電力を $E_a$[V]、 負荷電流を$I$[A]とすると、始動直後の電機子巻線抵抗 $R_a$[Ω]は、
$V=E_a+R_aI$
$12=0+R_a×4$
$R_a=3$[Ω]
定格運転時の誘導起電力 $E_{an}$[V]は、
$V=E_{an}+R_aI$
$12=E_{an}+3×1$
$E_{an}=9$[V]
入力電力を $P_i$[W]、出力電力を $P_o$[W]とすると、定格運転時の効率 $η$[%]は、
$η=\displaystyle\frac{P_o}{P_i}×100=\displaystyle\frac{E_{an}I}{VI}×100=\displaystyle\frac{9}{12}×100=75$[%]
答え (4)





