このページでは、波形整形回路(クリッパ回路とリミッタ回路)について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された波形整形回路(クリッパ回路とリミッタ回路)の過去問題の解き方も解説しています。
クリッパ回路とリミッタ回路
入力された電圧を、ある一定電圧で切り取って、残りの部分を出力する回路のことをクリッパといいます。クリッパのうち、波形の上の部分を切り取って、残りを出力する回路を「ピーククリッパ」といい、クリッパのうち、波形の底の部分を切り取って、残りを出力する回路を「ベースクリッパ」といいます。
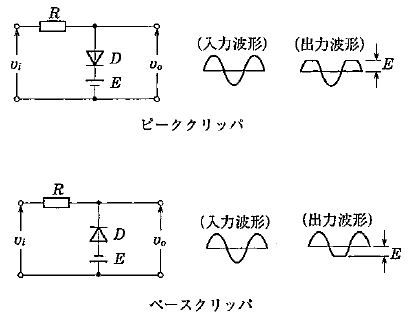
また、ベースクリッパとピーククリッパを組み合わせた回路をリミッタ回路といい、入力波形の振幅を制限する機能をもちます。
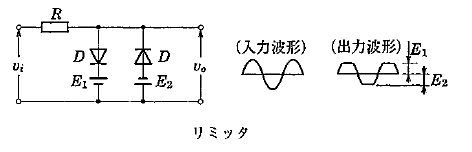
電験三種-理論(電子回路)過去問題
1999年(平成11年)問8
抵抗R、ダイオードD及び電池Eを図のような回路において、入力端子a、b間に正弦波電圧 $vi=Vmsinωt$ [V] を加えたとき、出力端子c、d間に生じる電圧 $v_o$ [V] の波形として、正しいのは次のうちどれか。 ただし、$V_m [V] >E [V] $とする。
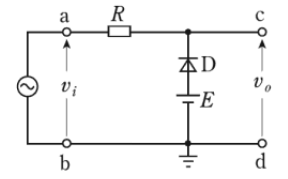

1999年(平成11年)問8 過去問解説
$v_i≧E$ の間のみ交流は $v_i$ の波形が $v_o$ に現れる回路です。(2)の波形が正解になります。
答え (2)
2012年(平成24年)問13
図は、抵抗 R1 [Ω] とダイオードからなるクリッパ回路に負荷となる抵抗 R2 [Ω] (=2R1 [Ω] )を接続した回路である。入力直流電圧 V [V] と R1 [Ω] に流れる電流 I [A] の関係を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、順電流が流れているときのダイオードの電圧は、0 [V] とする。また、逆電圧が与えられているダイオードの電流は、0 [A] とする。
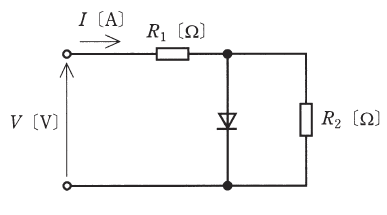
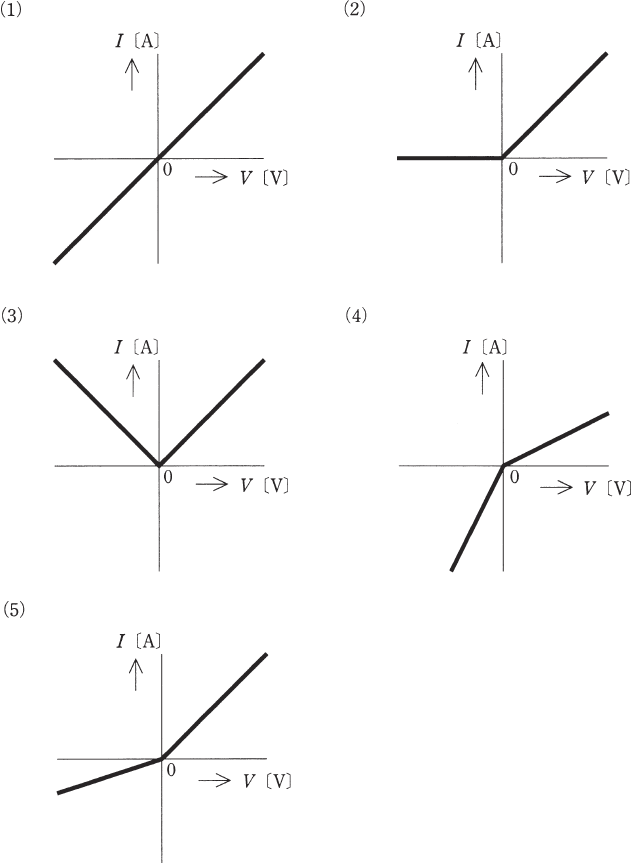
2012年(平成24年)問13 過去問解説
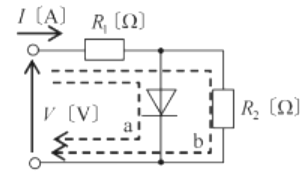
順電流が流れているときは、aに電流 $I$ が流れますので、
$I=\displaystyle\frac{V}{R_1}$
逆電流が流れているときは、bに電流 $I$ が流れますので、
$I=\displaystyle\frac{V}{R_1+R_2}=\displaystyle\frac{V}{3R_1}$
したがって(5)のグラフが正解になります。
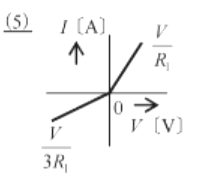
答え (5)
2014年(平成26年)問18
図1は、代表的なスイッチング電源回路の原理図を示している。次の(a)及び(b)の問に答えよ。
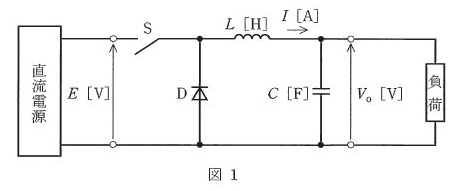
(a) 回路の説明として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- インダクタンス L [H] のコイルはスイッチSがオンのときに電磁エネルギーを蓄え、Sがオフのときに蓄えたエネルギーを放出する。
- ダイオード D は、スイッチSがオンのときには電流が流れず、Sがオフのときに電流が流れる。
- 静電容量 C [F] のコンデンサは出力電圧 Vo [V] を平滑化するための素子であり、静電容量 C [F] が大きいほどリプル電圧が小さい。
- コイルのインダクタンスやコンデンサの静電容量値を小さくするためには、スイッチSがオンとオフを繰り返す周期(スイッチング周期)を長くする。
- スイッチの実現には、バイポーラトランジスタや電界効果トランジスタが使用できる。
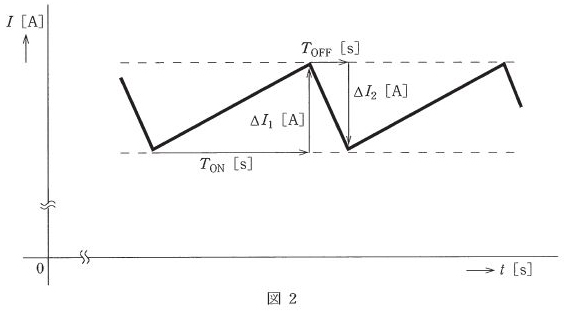
(b) スイッチSがオンの間にコイルの電流Iが増加する量をΔI1 [A] とし、スイッチSがオフの間にIが減少する量をΔI2 [A] とすると、定常的には図2の太線に示すような電流の変化がみられ、ΔI1 [A] =ΔI2 [A] が成り立つ。
ここで出力電圧 Vo [V] のリプルは十分小さく、出力電圧を一定とし、電流Iの増減は図2のように直線的であるとする。また、ダイオードの順方向電圧は0 Vと近似する。さらに、スイッチSがオン並びにオフしている時間をそれぞれ TON [S] 、TOFF [S] とする。
ΔI1 とVo を表す式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
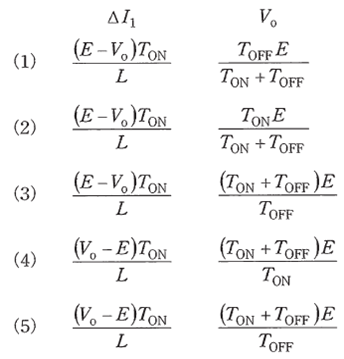
2014年(平成26年)問18 過去問解説
(a) コイルのインダクタンスやコンデンサの静電容量値を小さくするためには、スイッチSがオンとオフを繰り返す周期を短くする必要があります。したがって(4)の記述が誤りです。
答え (4)
(b) Sがオンのときのインダクタンス $L$ のコイルが発生する誘導起電力 $e$ と出力電圧 $V_o$ の関係は、
$E=e+V_o=L\displaystyle\frac{Δ{I_1}}{T_{on}}+V_o$
$Δ{I_1}=\displaystyle\frac{(E-V_o)T_{on}}{L}$
Sがオフのときは、コイルは電流を流し続ける向きに誘導起電力 $e$ が発生します。$e$ の大きさは、
$e=L\displaystyle\frac{Δ{I_2}}{T_{off}}=V_o$
$Δ{I_2}=\displaystyle\frac{V_o×T_{off}}{L}$
$ΔI_1=ΔI_2$より、
$\displaystyle\frac{(E-V_o)T_{on}}{L}=\displaystyle\frac{V_o×T_{off}}{L}$
$V_o=\displaystyle\frac{E×T_{on}}{T_{on}+T_{off}}$
答え (2)





