このページでは、オペアンプについて、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題されたオペアンプの過去問題の解き方も解説しています。
オペアンプとは?
オペアンプは演算増幅器ともいわれる、多目的に使える高性能な増幅回路です。高利得を要求される増幅回路や微積分回路、比較回路、発信回路などに利用されています。
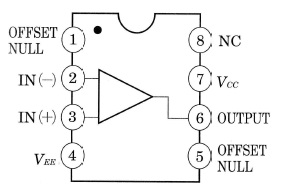
オペアンプはIC化された部品として使用するのが一般的です。オペアンプの図記号は、三角形で表します。オペアンプは2本の入力端子と1本の出力端子を持っており、2つの入力信号は単一信号に変換されます。オペアンプには、次のような特徴があります。
- 増幅度が非常に大きい($10^4$~$10^6$倍)
- 入力インピーダンスは高く(数100kΩ~数10MΩ)、出力インピーダンスは低い(数10Ω)
- 広い周波数帯域で使用できる
ただし、増幅度が大きくとれるといっても、ICに加える電源電圧以上の出力は得られません。これは、どの増幅回路についても同様です。オペアンプでは、出力が電源電圧と同じになれば飽和します。
反転増幅回路
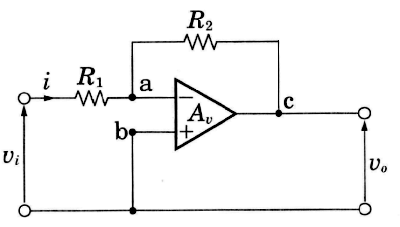
オペアンプの動作の基本は、「反転増幅回路」といわれるものです。この回路は、並列ー並列型の負帰還増幅回路になっています。
帰還のない場合は、端子cには、$v_o=-A_vv_i$ が出力されます。負帰還をかけた場合には、端子cの負電圧が $R_2$ を経由して戻されるために端子aの電位は下がります。この現象を連続するためには、端子aの電位は徐々に下がっていきます。そして端子aの電位がアースに対して負になると、端子cには正電圧が出力されます。すると、先ほどとは逆に、端子aの電位が高くなってきます。これらの動作は、増幅度の大きなオペアンプにおいては、一瞬にして行われるため、端子aの電位は常にゼロとなっていると考えて差支えありません。したがって実際の端子a-bの抵抗は非常に大きいにもかかわらず、入力端子a-bはショートしているように見えてしまいます。このことを「イマジナリショート(仮想短絡)」といいます。
端子aとbはイマジナリショートしているので、$R_1$ に流れる電流 $i$ は、次の式のようになります。
$i=\displaystyle\frac{v_i}{R_1}$
オペアンプの入力インピーダンスは、非常に高いため電流 $i$ は、オペアンプ内には流れずに $R_2$ を経由して端子cに向けて流れます。このため端子cの電圧 $v_o$ は、端子aの電位(ゼロ)よりも $R_2$ による電圧降下の分だけ低くなります。
$v_o=0-R_2i=-\displaystyle\frac{R_2}{R_1}v_i$
したがって、電圧増幅度は次のようになります。
$\displaystyle\frac{v_o}{v_i}=-\displaystyle\frac{R_2}{R_1}$
非反転増幅回路
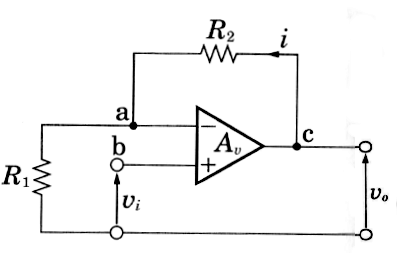
入力電圧と出力電圧を同相で増幅する回路を「非反転増幅回路」といいます。出力端子cから、抵抗 $R_2$ を経由して流れる電流 $i$ は、そのまま抵抗 $R_1$ に流れます。また、この回路でも負帰還によって入力端子aとbは、イマジナリショートしていると考えられます。したがって、入力電圧 $v_i$ は次の式のようになります。
$v_i=R_1i$
出力電圧 $v_o$ と電圧増幅度は次の式のようになります。
$v_o=(R_1+R_2)i$
$\displaystyle\frac{v_o}{v_i}=\displaystyle\frac{(R_1+R_2)i}{R_1i}=1+\displaystyle\frac{R_2}{R_1}$
つまり、非反転増幅回路では、増幅度は抵抗 $R_1$ と $R_2$ の比率によって決まります。また、この回路では並列ー直列型の負帰還増幅回路になっているため、オペアンプ自身の入出力インピーダンスより、入力インピーダンスは大きくなり、出力インピーダンスは小さくなります。
また、$R_1=∞$、$R_2=0$ とすれば、増幅度が1の電圧フォロアと呼ばれる回路として動作させることができます。
電験三種-理論(電子回路)過去問題
2003年(平成15年)問18
図のような演算増幅器を使用した直流回路において、抵抗 R1=10 [kΩ]、抵抗抵抗 R2=100 [kΩ] である。この回路に入力電圧 V1=0.5 [V] を加えたとき、次の(a)及び(b)に答よ。
ただし、演算増幅器は理想的な特性を持ち、その入力抵抗及び電圧増幅器度は極めて大きく、その出力抵抗は無視できるものとする。

(a) 演算増幅器の二つの入力端子の端末間電圧 Vi [V] の値として、正しいものは次のうちどれか。
(1) 0 (2) 0.1 (3) 0.5 (4) 1 (5) 5
(b) 演算増幅器の出力電圧 V2 [V] の値として、正しいのは次のうちどれか。
(1) -0.05 (2) -0.25 (3) -1 (4) -2.5 (5) -5
2003年(平成15年)問18 過去問解説
(a) 増幅器の増幅率を $A$ とすると、
$A=\displaystyle\frac{V_2}{V_i}$
題意より $A=∞$ ですので、$V_i=0$ になります。つまり、$A$ が大きければ大きいほど、$V_i$ はゼロに近づくことになります。これを「イマジナリショート」といいます。
答え (1)
(b) イマジナリーショートしているので、
$i=\displaystyle\frac{V_1}{R_1}$
$V_2=0-R_2i=-\displaystyle\frac{R_2}{R_1}V_1=-\displaystyle\frac{100}{10}×0.5=-5$[V]
答え (5)
2007年(平成19年)問12
演算増幅器に関する記述として、誤っているのは次のうちどれか。
- 利得が非常に大きい。
- 入力インピーダンスが非常に大きい。
- 出力インピーダンスが非常に小さい。
- 正相入力端子と逆相入力端子がある。
- 直流入力では使用できない。
2007年(平成19年)問12 過去問解説
演算増幅器は、直流入力で使用できます。したがって(5)が誤りです。
答え (5)
2010年(平成22年)問18
演算増幅器(オペアンプ)について、次の(a)及び(b)に答えよ。
(a) 演算増幅器の特徴に関する記述として,誤っているのは次のうちどれか。
- 反転増幅と非反転増幅の二つの入力端子と一つの出力端子がある。
- 直流を増幅できる。
- 入出力インピーダンスが大きい。
- 入力端子間の電圧のみを増幅して出力する一種の差動増幅器である。
- 増幅度が非常に大きい。
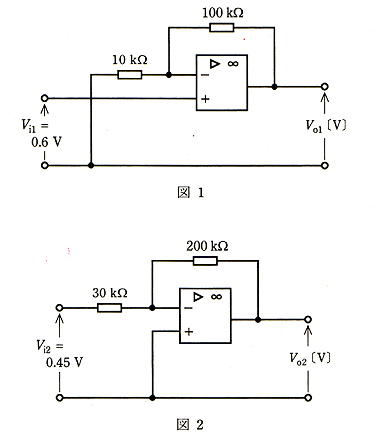
(b) 図1及び図2のような直流増幅回路がある。それぞれの出力電圧 Vo1[V],Vo2[V]の値として,正しいものを組み合わせたのは次のうちどれか。
ただし、演算増幅器は理想的なものとし、Vi1 = 0.6[V]及び Vi2 = 0.45[V]は入力電圧である。
| Vo1 | Vo2 | |
| (1) | 6.6 | 3.0 |
| (2) | 6.6 | -3.0 |
| (3) | -6.6 | 3.0 |
| (4) | -4.5 | 9.0 |
| (5) | 4.5 | -9.0 |
2010年(平成22年)問18 過去問解説
(a) オペアンプは入力インピーダンスが大きく、出力インピーダンスは小さいのが特徴です。したがって(3)が誤りです。
答え (3)
(b) 図1は非反転増幅回路です。非反転増幅回路の増幅度は、
$\displaystyle\frac{V_o}{V_i}=1+\displaystyle\frac{R_2}{R_1}$
ですので、
$V_{o1}=(1+\displaystyle\frac{R_2}{R_1})V_{i1}=(1+\displaystyle\frac{100}{10})×0.6=6.6$[V]
図2は反転増幅回路です。反転増幅回路の増幅度は、
$\displaystyle\frac{V_o}{V_i}=-\displaystyle\frac{R_2}{R_1}$
$V_{o2}=-\displaystyle\frac{R_2}{R_1}V_{i2}=-\displaystyle\frac{200}{30}×0.45=-3$[V]
答え (2)
2014年(平成26年)問13
図のような、演算増幅器を用いた能動回路がある。直流入力電圧 Vin [V] が 3V のとき、出力電圧 Vout [V] として、最も近い Vout の値を次の(1)~(5)のうちから一つ選べ。
ただし、演算増幅器は、理想的なものとする。
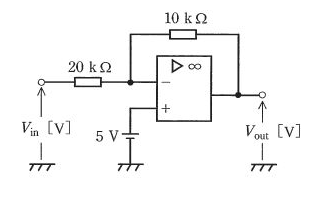
(1) 1.5 (2) 5 (3) 5.5 (4) 6 (5) 6.5
2014年(平成26年)問13 過去問解説
オペアンプの入力インピーダンスは∞で、入力端子間は短絡状態となりますので、
$I_{in}=\displaystyle\frac{V_{in}-5}{20×10^3}=\displaystyle\frac{3-5}{20×10^3}=-0.1×10^{-3}$[A]
$\begin{eqnarray}V_{out}&=&5-10×10^3×I_{in}\\&=&5-10×10^3×(-0.1×10^{-3})\\&=&6[V]\end{eqnarray} $
答え (4)
2015年(平成27年)問18
演算増幅器(オペアンプ)について、次の(a)及び(b)の問に答えよ。
(a) 演算増幅器は、その二つの入力端子に加えられた信号の( ア )を高い利得で増幅する回路である。演算増幅器の入力インピーダンスは極めて( イ )ため、入力端子電流は( ウ )とみなしてよい。一方、演算増幅器の出力インピーダンスは非常に( エ )ため、その出力端子電圧は負荷による影響を( オ )。さらに、演算増幅器は利得が非常に大きいため、抵抗などの部品を用いて負帰還をかけたときに安定した有限の電圧利得が得られる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 差動成分 | 大きい | ほぼ零 | 小さい | 受けにくい |
| (2) | 差動成分 | 小さい | ほぼ零 | 大きい | 受けやすい |
| (3) | 差動成分 | 大きい | 極めて大きな値 | 大きい | 受けやすい |
| (4) | 同相成分 | 大きい | ほぼ零 | 小さい | 受けやすい |
| (5) | 同相成分 | 小さい | 極めて大きな値 | 大きい | 受けにくい |
(b) 図のような直流増幅回路がある。この回路に入力電圧 0.5V を加えたとき、出力電圧 Vo の値 [V] と電圧利得 Av の値 [dB] の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、演算増幅器は理想的なものとし、log102=0.301、log103=0.477とする。
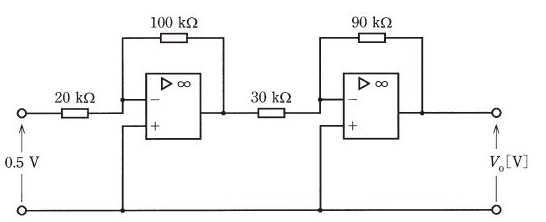
Vo Av
(1) 7.5 12
(2) -15 12
(3) -7.5 24
(4) 15 24
(5) 7.5 24
2015年(平成27年)問18 過去問解説
(a) 演算増幅器は、その二つの入力端子に加えられた信号の( 差動成分 )を高い利得で増幅する回路である。演算増幅器の入力インピーダンスは極めて( 大きい )ため、入力端子電流は( ほぼ零 )とみなしてよい。一方、演算増幅器の出力インピーダンスは非常に( 小さい )ため、その出力端子電圧は負荷による影響を( 受けにくい )。さらに、演算増幅器は利得が非常に大きいため、抵抗などの部品を用いて負帰還をかけたときに安定した有限の電圧利得が得られる。
答え (1)
(b) 反転増幅回路を2段に直列接続しています。1段の増幅度は
$\displaystyle\frac{V_o}{V_i}=-\displaystyle\frac{R_2}{R_1}$
ですので、
$V_o=\left(-\displaystyle\frac{100}{20}×0.5\right)×\left(-\displaystyle\frac{90}{30}\right)=7.5$ [V]
電圧利得は、
$\begin{eqnarray}A_V&=&20log_{10}\displaystyle\frac{7.5}{0.5}\\\\&=&20log_{10}\displaystyle\frac{3×10}{2}\\\\&=&20log_{10}3+20log_{10}10-20log_{10}2\\\\&≒&24[dB] \end{eqnarray}$
答え (5)
2017年(平成29年)問18
演算増幅器を用いた回路について、次の(a)及び(b)の問に答えよ。
(a) 図1の回路の電圧増幅度 $\displaystyle\frac {ν_o}{ν_i}$ を $3$ とするためには、$α$ をいくらにする必要があるか。$α$ の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
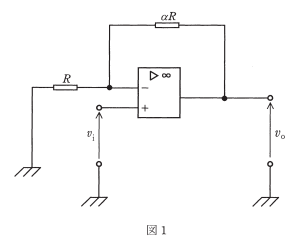
(1) 0.3 (2) 0.5 (3) 1 (4) 2 (5) 3
(b) 図2の回路は、図1の回路に、帰還回路として2個の $5kΩ$ の抵抗と2個の $0.1µF$ のコンデンサを追加した発振回路である。発振の条件を用いて発振周波数の値 $f$[kHz]を求め、最も近いものを次の(1)~(5)のうちから一つ選べ。
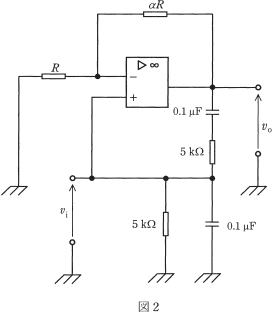
(1) 0.2 (2) 0.3 (3) 0.5 (4) 2 (5) 3
2017年(平成29年)問18 過去問解説
(a) オペアンプの入力インピーダンスは∞で、入力端子間は短絡状態となりますので、
$\displaystyle\frac{ν_o-v_i}{aR}=\displaystyle\frac{v_i}{R}$
$\displaystyle\frac {ν_o}{ν_i}=a+1$
$3=a+1$
$a=2$
答え(4)
(b)ウィーンブリッジ発振回路です。この回路の発振周波数 $f$[Hz]は、次の式で求めることができます。
$f=\displaystyle\frac {1}{2π\sqrt{C_1C_2R_1R_2}}$
$f=\displaystyle\frac {1}{2π\sqrt{(0.1×10^{-6})^2×(5×10^3)^2}}≒318$[Hz]
答え(2)





