第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「直流発電機の種類と特性」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「直流発電機の種類と特性」の過去問題も解説しています。
直流発電機の起電力
磁極数を $p$、電機子導体数を $Z$、磁極の磁束を $ϕ$[Wb]、回転数を $n$[rpm]、電機子の並列回路数を $a$ とすると、直流発電機全体の誘導起電力 $E$[V]は、次の式で表すことができます。
直流発電機の誘導起電力を求める式
$E=\displaystyle\frac{pZ}{60a}ϕn=K_1ϕn$
$E$[V]:直流発電機に発生する誘導起電力
$Z$:全導体数 (全コイル数)
$a$:並列回路数
$p$:磁極数
$ϕ$[Wb]:磁束(磁極1極あたりの磁束)
$n$[min-1]:電機子の回転速度
$K_1=\displaystyle\frac{pZ}{60a}$ :電圧定数(比例定数)
並列回路数 $a$ は、重ね巻では $a=p$、波巻では $a=2$ となります。
誘導起電力 $E$[V]は、磁束 $ϕ$[Wb]と回転数 $n$[rpm]に比例します。つまり、強い磁力と速い回転力を与えることにより、大きな起電力を得ることが出来ます。
直流発電機の誘導起電力と負荷電流
界磁鉄心は界磁巻線に電流が流れる事で磁化されます。直流発電機では界磁をどのように磁化するかによって、他励式と自励式に分類されます。
- 他励式 … 界磁巻線の励磁電流を別の電源から取る方式
- 自励式 … 界磁巻線の励磁電流を自己の起電力から取る方式。自励式には分巻式、直巻式、複巻式があります
他励発電機
他励発電機の原理図と回路図を示します。界磁巻線 $F_C$ に流す界磁電流 $I_f$[A]は外部の電源 $V_f$[V]から供給されます。このような直流発電機を「他励発電機」といいます。
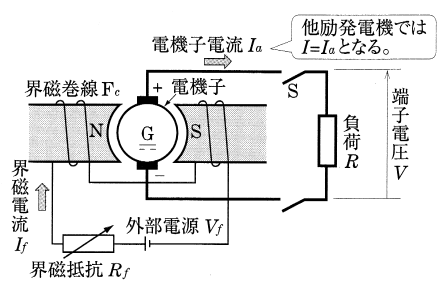

無負荷飽和曲線
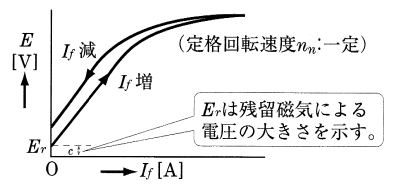
スイッチSを開いた状態で、電機子を定格回転速度 $n_n$[min-1]で回転させ、界磁電流 $I_f$[A]を増加すると、起電力 $E$[V]は界磁電流 $I_f$[A]にほぼ比例して大きくなります。しかし、界磁電流 $I_f$[A]がある大きさ以上になると、鉄心の磁気飽和のため、起電力 $E$[V]は増加しなくなります。次に、界磁電流 $I_f$[A]を最大値から減少すると、鉄心のヒステリシスのため起電力 $E$[V]の値は一致しません。尚、$E_r$[V]は鉄心の残留磁気による起電力です。
このように無負荷の状態において界磁電流 $I_f$[A]と起電力 $E$[V]との関係を示す曲線を「無負荷飽和曲線」といいます。
外部特性曲線
スイッチを閉じて、直流発電機を定格回転速度 $n_n$[min-1]で回転させ、定格電圧 $V_n$[V]のときに、定格電流 $I_n$[A]となるように界磁抵抗 $R_f$[Ω]と負荷抵抗 $R_L$[Ω]を調整します。回転速度 $n_n$[min-1]、界磁電流 $I_f$[A]を変えないで、負荷抵抗 $R_L$[Ω]を変化させるときの負荷電流 $I$[A]と端子電圧 $V$[V]との関係を示す曲線を外部特性曲線といいます。

図は、外部特性曲線の例で、負荷電流 $I$[A]の増加にともなって端子電圧 $V$[V]が減少します。これは電機子巻線抵抗 $R_a$[Ω]による電圧降下 $R_aI$[V]、電機子反作用による電圧降下 $v_a$[V] 、ブラシ接触電圧降下 $v_b$[V]があるためです。端子電圧 $V$[V]と起電力 $E$[V]の関係は、次の式で表すことができます。
$V=E- (I_aR_a+v_a+v_b )$[V]
他励発電機回路の各値
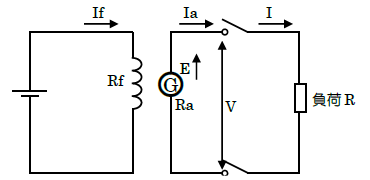
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$I_aR_a$:電機子抵抗による電圧降下
電流の関係式
$I=I_a$
他励発電機における各種公式
起電力:$E=K_1ϕn$
端子電圧:$V=E- (I_aR_a+v_a+v_b )$
発電機の出力:$P_o=VI=I^2R$
自励発電機
直流発電機において、自己の誘導起電力を利用して磁極を励磁すれば、外部の直流電源は不要になります。このような発電機を「自励発電機」といいます。
この場合、電機子巻線と界磁巻線の接続のしかたによって、「分巻発電機・直巻発電機・複巻発電機」などがあります。
分巻発電機
次の図のように、電機子と界磁巻線が並列に接続されたものを「分巻発電機」といいます。
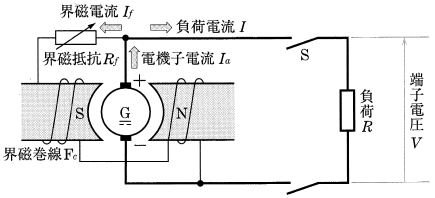
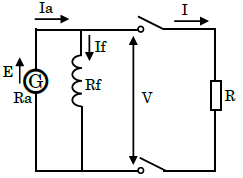
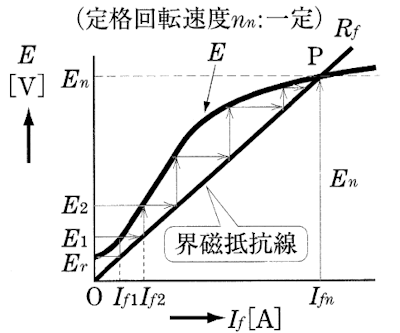
電機子が回転すれば、まず磁極の残留磁束によって、電機子巻線に $E_r$[V]の起電力が誘導され、それによって界磁巻線に $I_{f1}$[A]の電流が流れます。$I_{f1}$[A]の電流による磁束と残留磁束の向きが同じであれば、それらの和の磁束によって電機子巻線に $E_1$[V]の起電力が誘導され、界磁巻線に $I_{f2}$[A]の電流が流れます。さらには $I_{f2}$[A]の電流によって、電機子巻線には $E_2$[V]の起電力が誘導されます。
このような経過をすばやくたどって、電機子巻線には安定した起電力 $E_n$[V]が得られることになります。また、$\overline{OP}$ を界磁抵抗線とよんでいます。
分巻発電機の外部特性曲線は、定格値の範囲では負荷電流に比例して端子電圧は減少し、その値は小さくなります。この場合の端子電圧 $V$[V]と起電力 $E$[V]の関係は、次の式で表すことができます。
$V=E-(I_aR_a+v_a+v_b+v_f ) $[V]
ただし、$I_a=I+I_f$,$I_f=\displaystyle\frac{V}{R_f}$

分巻発電機は、負荷電流 $I$[A]が増えると、電機子巻線抵抗による電圧降下も増えるため、端子電圧 $V$[V]は下がります。
負荷電流 $I$[A]を、定格電流 $I_{n}$[A]よりさらに大きくすると、電流の最大値の点bを通って点cに達し、安定な運転ができません。
分巻発電機回路の各値
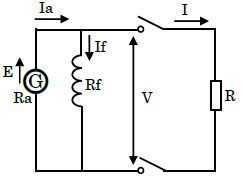
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$v_f$:界磁電流の低下による電圧降下
$I_aR_a$:電機子抵抗による電圧降下
電流の関係式
$I_a=I+I_f$,$I_f=\displaystyle\frac{V}{R_f}$
分巻発電機における各種公式
起電力:$E=K_1ϕn$
端子電圧:$V=E-(I_aR_a+v_a+v_b+v_f ) $
発電機の出力:$P_o=VI=I^2R$
直巻発電機
図のように電機子と界磁巻線が直列に接続されたものを「直巻発電機」といいます。
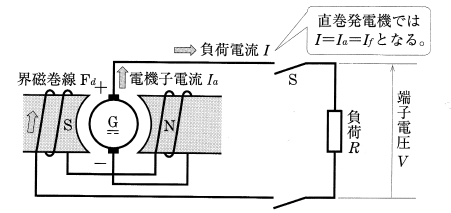
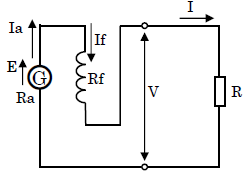
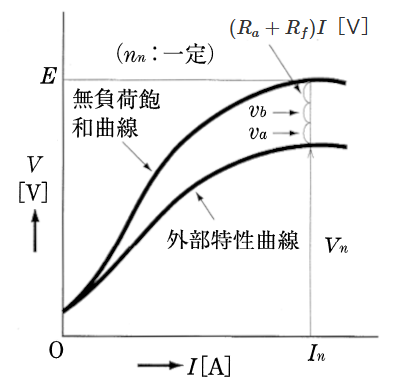
直巻発電機の外部特性曲線は、界磁巻線を切り離し、他励発電機として無負荷飽和曲線を求め、この曲線から電機子巻線抵抗と界磁巻線抵抗の電圧降下 $(R_a+R_f)I$[V]、電機子反作用による電圧降下 $v_a$[V]およびブラシ接触電圧降下 $V_b$[V]を差し引いて描いたものです。したがって、端子電圧 $V$[V]と起電力 $E$[V]の関係は、これらの関係より次の式で表すことができます。
$V=E-{(R_a+R_f)I+v_a+v_b}$[V]
分巻発電機回路の各値
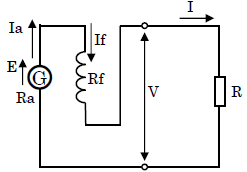
$I_f$:界磁電流,$Rf$:界磁抵抗
$V$:端子電圧,$I$:負荷電流
$E$:誘導起電力
$I_a$:電機子電流
$R_a$:電機子抵抗
$v_a$:電機子反作用による電圧降下
$v_b$:ブラシによる電圧降下
$I_aR_a$:電機子抵抗による電圧降下
$I_fR_f$:界磁巻線抵抗による電圧降下
電流の関係式
$I_a=I_f=I$
分巻発電機における各種公式
起電力:$E=K_1ϕn$
端子電圧:$V=E-{(R_a+R_f)I+v_a+v_b}$
発電機の出力:$P_o=VI=I^2R$
複巻発電機
複巻発電機は、 2 つの界磁コイルを持ち、 1 つは電機子コイルと直列に、もう 1 つは電機子コイルと並列に接続します。その際、 2 つの界磁コイルの接続極性が、互いに磁束を増加させる向きに接続する方法を「和動複巻」、互いに磁束が相反する向きに接続する方法を「差動複巻」といいます。一般的には、和動複巻が多く使われています。
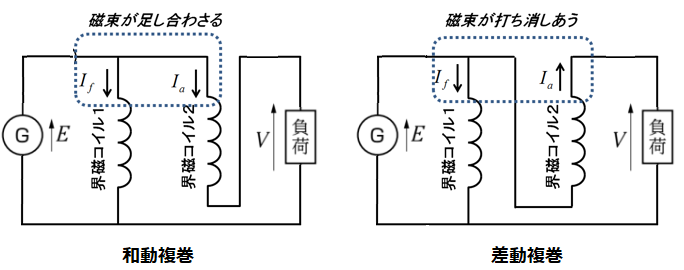
複巻式は、分巻式と直巻式を組み合わせた方式で、発電機の場合は分巻界磁が直巻界磁より電機子側にあり、「内分巻」といいます。尚、電動機の場合は分巻界磁が端子側にあり、「外分巻」といいます。
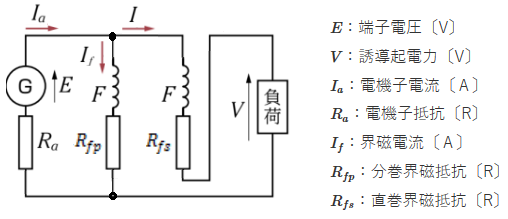
複巻発電機における各種公式
起電力:$E=K_1ϕn$
端子電圧:$V=E-I_aR_a-IR_{fs}=I_fR_{fp}-IR_{fs}$
発電機の出力:$P_o=VI=I^2R$
電流の関係式:$I_a=I+I_f$
電験三種-機械の過去問解説:直流発電機の種類と特性
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
2001年(平成13年)問1
直流電動機が回転しているとき、導体は磁束を切るので起電力を誘導する。この起電力の向きは、フレミングの( ア )によって定まり、外部から加えられる直流電圧とは逆向き、すなわち電機子電流を減少させる向きとなる。このため、この誘導起電力は逆起電力と呼ばれている。直流電動機の機械的負荷が増加して( イ )が低下すると、逆起電力は( ウ )する。これにより、電機子電流が増加するので( エ )も増加し、機械的負荷の変化に対応するようになる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 右手の法則 | 回転速度 | 減少 | 電機子の入力 |
| (2) | 右手の法則 | 磁束密度 | 増加 | 電機子の入力 |
| (3) | 左手の法則 | 回転速度 | 増加 | 電機子の入力 |
| (4) | 左手の法則 | 磁束密度 | 増加 | 電機子反作用 |
| (5) | 左手の法則 | 回転速度 | 減少 | 電機子反作用 |
2001年(平成13年)問1 過去問解説
直流電動機が回転しているとき、導体は磁束を切るので起電力を誘導する。この起電力の向きは、フレミングの( 右手の法則 )によって定まり、外部から加えられる直流電圧とは逆向き、すなわち電機子電流を減少させる向きとなる。このため、この誘導起電力は逆起電力と呼ばれている。直流電動機の機械的負荷が増加して( 回転速度 )が低下すると、逆起電力は( 減少 )する。これにより、電機子電流が増加するので( 電機子の入力 )も増加し、機械的負荷の変化に対応するようになる。
答え (1)
2002年(平成14年)問1
出力40[KW]、端子電圧200[V]、回転速度1,500[min-1]で運転中の他励直流発電機がある。この発電機の負荷電流及び界磁電流を一定に保ったまま、回転速度を1,000[min-1]に低下させた。この場合の誘導起電力[V]の値として、正しいのは次のうちどれか。
ただし、電機子回路の抵抗は0.05[Ω]とし、電機子反作用は無視できるものとする。
(1)126 (2)133 (3)140 (4)200 (5)210
2002年(平成14年)問1 過去問解説
問題を図に示します。
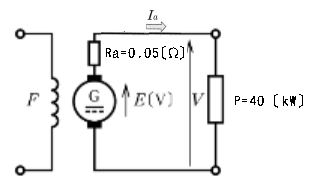
発電機の負荷電流を $I_a$[A]、 誘導起電力を $E$[V]とすると、
$I_a=\displaystyle\frac{P}{V}= \displaystyle\frac {40×10^3}{200}=200$[A]
$E=R_aI+V=0.05×200+200=210$[V]
誘導起電力を $E$[V]は、$E=K_1ϕn$ ですので、1,500[min-1]回転と1,000[min-1]回転
1,500[min-1]回転のとき:$210=K_1ϕ×1500$ …(1)
1,000[min-1]回転のとき:$E_{2}=K_1ϕ×1000$ …(2)
(1),(2)式を解くと、
$E_{2}=210×\displaystyle\frac{100}{1500}=140$[V]
答え (3)
2009年(平成21年)問1
直流発電機に関する記述として、正しいのは次のうちどれか。
- 直巻発電機は、負荷を接続しなくても電圧の確立ができる。
- 平複巻発電機は、全負荷電圧が無負荷電圧と等しくなるように(電圧変動率が零になるように)直巻巻線の起磁力を調整した発電機である。
- 他励発電機は、界磁巻線の接続方向や電機子の回転方向よっては電圧の確立ができない場合がある。
- 分巻発電機は、負荷電流によって端子電圧が降下すると、界磁電流が増加するので、他励発電機より負荷による電圧変動が小さい。
- 分巻発電機は、残留磁気があれば分巻巻線の接続方向や電機子の回転方向に関係なく電圧の確立ができる。
2009年(平成21年)問1 過去問解説
- 直巻発電機は、負荷を接続しないと界磁電流が流れず、電圧の確立ができません。
- 正しい記述です。
- 他励発電機は、界磁巻線の接続方向や電機子の回転方向によらず電圧の確立ができます。
- 分巻発電機は、負荷電流によって端子電圧が降下すると、界磁電流も低下するので、他励発電機より負荷による電圧変動は大きくなります。
- 分巻発電機は、残留磁気があっても分巻巻線の接続方向や電機子の回転方向により、残留磁気を打ち消すので電圧の確立ができません。
答え (2)
電験三種の機械科目に出題される「直流機」のページ
- 直流機の原理と構造
- 直流機の電機子反作用
- 直流発電機の種類と特性
- 直流電動機の種類と特性
- 直流電動機の始動と速度制御
- 直流機の定格






