これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「コンデンサとリアクトル」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。
コンデンサのしくみ
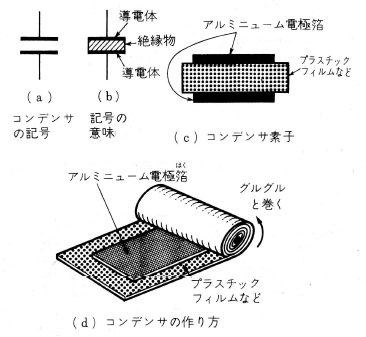
コンデンサ(condenser)は、第1図(a)のような記号で表わしますが、これは第1図(b)のように導電体の間にサンドイッチ状に絶縁物が入っていることを示しています。導電体には第1図(C)のようにアルミニウム箔を使い、絶縁物にはプラスチックフィルムや油浸絶縁紙を使い、第1図(d)のようにグルグル巻いてコンデンサを作ります。
コンデンサの特性
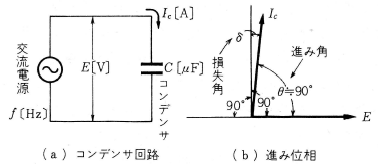
第2図(a)のようにコンデンサに交流電圧 $E$ を加えると、コンデンサには電流 $I_c$ 流れますが、第2図(b)のように電流 $I_c$ は電圧 $E$ よりほぼ90°( $\displaystyle\frac{π}{2}$ rad)進んだ位相で流れます。コンデンサの電流は進み電流であるというのが、コンデンサの大きな特性です。
コンデンサの容量 $Q$〔kVA〕は、第2図(a)では、
$Q=2πfCE^2× 10^{-9}$〔kVA〕
$f$:周波数〔Hz〕
$E$:電圧〔V〕
$C$:静電容量〔μF〕
となります。
コンデンサは第1図(C)のように電極間に絶縁物が入っており、絶縁物による熱損失が発生します。このため第2図(b)のように電流 $I_C$ の進み角 $θ$ は、正確 に90°ではなく
$90° >θ =90° -δ$
となり、$δ$ を損失角といます。損失 $p$ 〔W〕とは次の関係があります。
$p=2πfCE^2× 10^{-9}×tanδ〔kw〕=Qtanδ〔kW〕$
リアクトルのしくみ
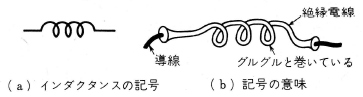
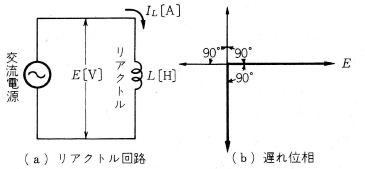
リアクトル(reactor)は、第3図(a)のような記号で表わしますが、これは第3図(b)のように絶縁電線をグルグル巻いて作られていることを示しています。
リアクトルの特性
第4図(a)のように交流電圧 $E$ を加えると、リアクトルには電流 $I_L$ が流れますが、(b)のように電流 $U_L$ は電圧 $E$ よりほぼ90°($\displaystyle\frac{π}{2}$)遅れた位相の電流が流れます。つまり、リアクトルの電流 $I_L$ とコンデンサの電流 $I_C$ (第2図(b))は、ほぼ180°の位相差があります。
リアクトルの応用
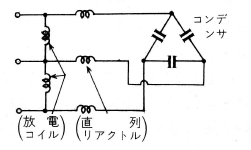
ビルや工場では、リアクトルを活用する場は広くはありません。第5図のように力率改善用コンデンサの直列リアクトル及び放電コイルに用いられています。
直列リアクトルは、コンデンサにより電圧波形が悪くなるのを防ぐ目的で入れられており、コンデンサ容量の6%の容量を有しています。放電コイルは、コンデンサ開放時に、 5秒以内にコンデンサ端子電圧を50V以下にするように電荷を放電するように使っています。
コンデンサの応用
力率とは
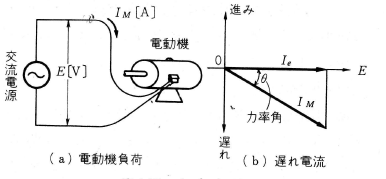
第6図(a)のように負荷として誘導電動機があり、これに交流電圧 $E$ を加えて運転すると、負荷電流 $I_M$ が流れ、第6図(b)のように負荷電流 $I_M$ は交流電圧 $E$ より角 $θ$ °遅れるのが一般的です。角 $θ$ の $cos$ を取って、$cosθ$ を力率といいますが、力率を%で表わすときは、
%で表わした力率$=100×cosθ$
となります。
力率改善とは
一般に電気負荷(電動機,蛍光灯,溶接機など)は、第6図(b)のように、負荷電流は電圧より遅れ、このとき $cos θ$ を遅れ力率といいます。$cosθ$ を100%に近づけることを力率改善といい、省エネルギーや電気料金の低減と大きな関係があります。
力率改善で安くなる電気料金
電力会社では、需用家の力率が良くなれば、電気料金を安くする電気料金制度を採用しています。電気料金は、契約電力〔kW〕で決まる基本料金と、使用電力量〔kWH〕で決まる電力量料金の和になっています。

電気料金の中の基本料金は、力率が85〔%〕以上に良くなれば、安くなることを示しています。つまり、

になり、力率を85%から95%に改善すると、基本料金も10%も安くなります。
力率改善用コンデンサ容量の求め方
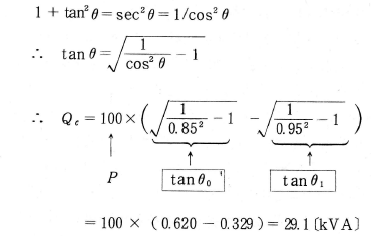
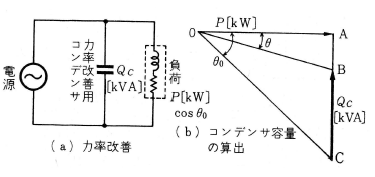
第7図(a)のように負荷に力率改善用コンデンサ $Q_C$ 〔kVA〕を設置して、力率を $coscθ_O$ から $COSθ$ に改善するときのベクトル図は第7図(b)のようになります。したがって、力率改善用コンデンサの容量 $Q_C $ は、
$Q_C =\overline{ AC }-\overline{ AB }=Ptanθ_O-Ptanθ_1$
∴$Q_C=P(tanθ_O-tanθ_1)$〔kVA〕
ただしPは負荷の有効電力〔kW〕
計算例
いま、100kW、遅れ力率85%の負荷に力率改善用コンデンサを設置して、遅れ力率95%にするために必要なコンデンサ容量を求めると、つぎのようになります。