第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「論理回路とn進数」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「論理回路とn進数」の過去問題も解説しています。
- 論理回路(ロジック回路)の基本回路
- 論理回路の組合せ回路
- 論理演算
- フリップフロップ回路
- 2進数と16進数
- 電験三種-機械の過去問解説:論理回路とn進数
- 1997年(平成9年)問14
- 1997年(平成9年)問14 過去問解説
- 1998年(平成10年)問11
- 1998年(平成10年)問11 過去問解説
- 1999年(平成11年)問11
- 1999年(平成11年)問11 過去問解説
- 1999年(平成11年)問14
- 1999年(平成11年)問14 過去問解説
- 2000年(平成12年)問11
- 2000年(平成12年)問11 過去問解説
- 2001年(平成13年)問11
- 2001年(平成13年)問11 過去問解説
- 2001年(平成13年)問14
- 2001年(平成13年)問14 過去問解説
- 2002年(平成14年)問11
- 2002年(平成14年)問11 過去問解説
- 2003年(平成15年)問14
- 2003年(平成15年)問14 過去問解説
- 2004年(平成16年)問14
- 2004年(平成16年)問14 過去問解説
- 2004年(平成16年)問18
- 2004年(平成16年)問18 過去問解説
- 2005年(平成17年)問14
- 2005年(平成17年)問14 過去問解説
- 2006年(平成18年)問14
- 2006年(平成18年)問14 過去問解説
- 2006年(平成18年)問18
- 2006年(平成18年)問18 過去問解説
- 2007年(平成19年)問14
- 2007年(平成19年)問14 過去問解説
- 2009年(平成21年)問14
- 2009年(平成21年)問14 過去問解説
- 2009年(平成21年)問18
- 2009年(平成21年)問18 過去問解説
- 2010年(平成22年)問14
- 2010年(平成22年)問14 過去問解説
- 2010年(平成22年)問18
- 2010年(平成22年)問18 過去問解説
- 2011年(平成23年)問14
- 2011年(平成23年)問14 過去問解説
- 2011年(平成23年)問18
- 2011年(平成23年)問18 過去問解説
- 2012年(平成24年)問14
- 2012年(平成24年)問14 過去問解説
- 2013年(平成25年)問14
- 2013年(平成25年)問14 過去問解説
- 2013年(平成25年)問18
- 2013年(平成25年)問18 過去問解説
- 2014年(平成26年)問18
- 2014年(平成26年)問18 過去問解説
- 2015年(平成27年)問14
- 2015年(平成27年)問14 過去問解説
- 2016年(平成28年)問14
- 2016年(平成28年)問14 過去問解説
- 2016年(平成28年)問18 過去問解説
- 2016年(平成28年)問18 過去問解説
- 2017年(平成29年)問14
- 2017年(平成29年)問14 過去問解説
論理回路(ロジック回路)の基本回路
入力に応じて一定の論理により出力する回路を論理回路またはロジック回路といいます。入力信号 1 or 0 の組合せで出力信号を表現できます。論理回路の基本回路としては、AND回路、OR回路、NOT回路があります。
AND回路(論理積回路)
AND回路は入力信号が全て 1(ON)になった時に出力信号が出る回路です。AND回路の図記号は次のように表します。
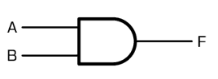
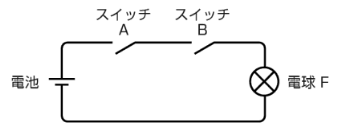
AND回路の動作は次のような電気回路で、表すことができます。
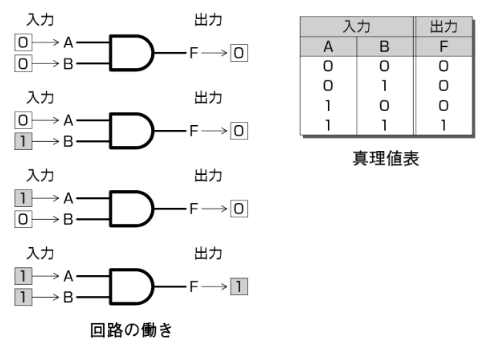
AND回路の働き、真理値表は次のとおりです。
OR回路(論理和回路)
OR回路は入力信号が一つでも 1(ON)になった時に出力信号が出る回路です。OR回路の図記号は次のように表します。
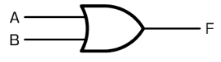
OR回路の動作は次のような電気回路で、表すことができます。
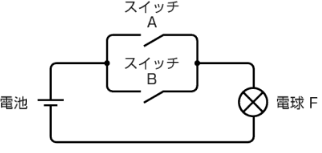
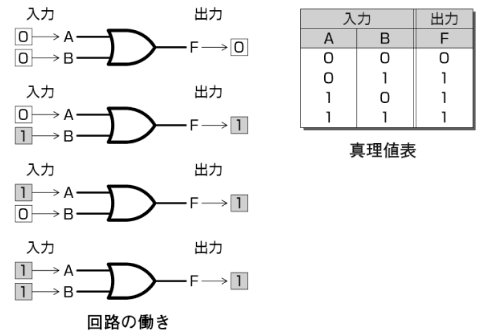
OR回路の働き、真理値表は次のとおりです。
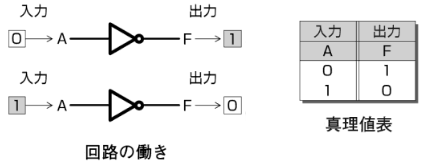
NOT回路(否定論理回路)
NOT回路は入力信号が 0(OFF)になった時に出力信号が出る回路です。NOT回路の図記号は次のように表します。
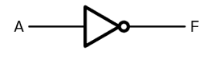
NOT回路の動作は次のような電気回路で、表すことができます。
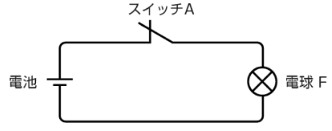
NOT回路の働き、真理値表は次のとおりです。
論理回路の組合せ回路
論理回路を組合せた回路を紹介します。
NAND回路(否定論理積回路)
AND回路の出力を否定させた回路です。NAND回路の図記号は次のように表します。
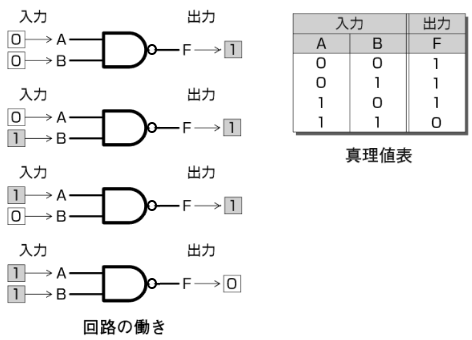
NAND回路の働き、真理値表は次のとおりです。
NOR回路(否定論理和回路)
OR回路の出力を否定させた回路です。NOR回路の図記号は次のように表します。
NOR回路の働き、真理値表は次のとおりです。
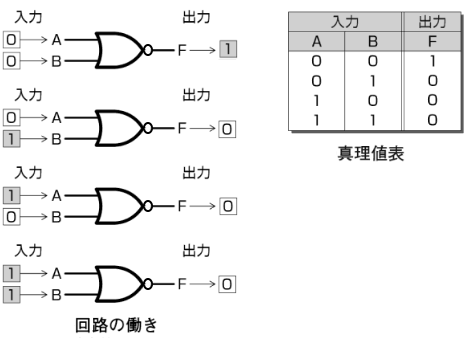
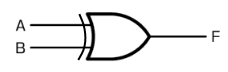
EX-OR回路(排他的論理和回路)
入力信号が等しくない時に信号が出て、入力信号が等しい時には出力が 0(OFF)になる回路です。EX-OR回路の図記号は次のように表します。
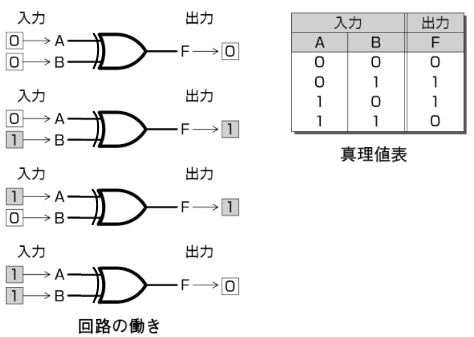
EX-OR回路の働き、真理値表は次のとおりです。
論理演算
デジタル回路の設計においては、複雑な変数間の関係を真理値表のような形ではなく、簡単な式の形式で表すと便利です。そのため、0と1で表されるディジタル値の論理演算は、ブール代数(論理代数)に従います。ブール代数は、2進数の算術方法ともいえます。
ブール代数の基本演算
| AND | OR | NOT |
|---|---|---|
| $A・B=Y$ | $A+B=Y$ | $\bar{ A}=Y$ |
| $0・0=0$ $0・1=0$ $1・0=0$ $1・1=1$ | $0+0=0$ $0+1=1$ $1+0=1$ $1+1=1$ | $\bar{ 0}=1$ $\bar{ 1}=0$ |
1変数のブール代数則
| AND | OR |
|---|---|
| $A・0=0$ $A・1=A$ $A・A=A$ $A・\bar{ A}=0$ | $A+0=A$ $A+1=1$ $A+A=A$ $A+\bar{ A}=1$ |
2変数以上のブール代数則
| 交換則 | $A+B=B+A$ $A・B=B・A$ |
| 結合則 | $A+(B+C)=(A+B)+C$ $A・(B・C)=(A・B)・C$ |
| 分配則 | $A・(B+C)=A・B+A・C$ $A+(B・C)=(A+B)・(A+C)$ |
| 吸収則 | $A+(A・B)=A$ $A・(A+B)=A$ $A+\bar{ A}・B=A+B$ |
| ドモルガンの定理 | $\overline{A+B}=\bar{ A}・\bar{ B}$ $\overline{A・B}=\bar{ A}+\bar{ B}$ |
フリップフロップ回路
基本論理回路を組み合わせて構成される回路に、フリップフロップ回路があります。フリップフロップ回路は順序回路の一つで、デジタル回路において重要かつ基本的な役割をしています。
フリップフロップ回路は、次の信号が来るまで出力状態を保持する回路です。
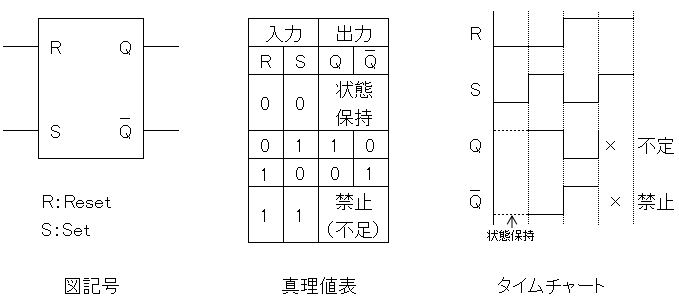
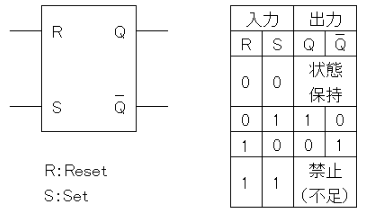
RSフリップフロップ
最も基本的なフリップフロップ回路です。二つの入力信号によって、その出力状態をリセット(Reset)された状態またはセット(Set)された状態に保持します。
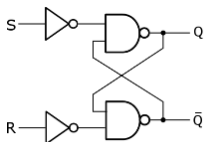
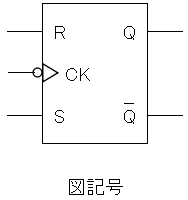
同期式フリップフロップ
CK端子(クロック)に入力される信号により、入力の読み込みと出力のタイミングが同期して動作するフリップフロップです。

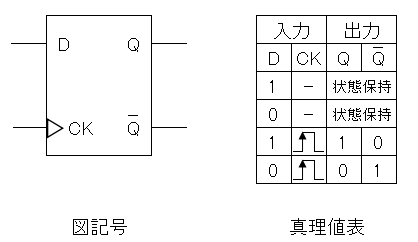
Dフリップフロップ
CK端子に入力された信号のタイミングで、D端子に入力された信号がQ端子に出力されるフリップフロップです。
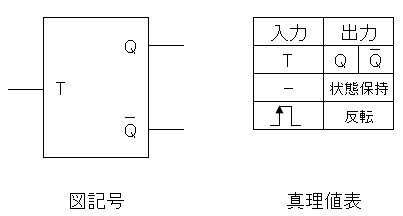
Tフリップフロップ
入力端子Tに信号が加えられると、出力Qが反転するフリップフロップです。
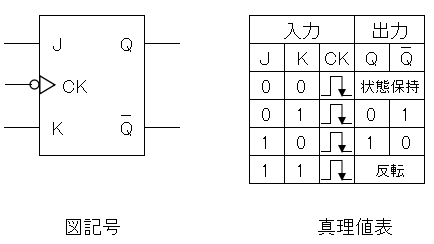
JKフリップフロップ
入力端子JとKの状態の組み合わせにより、出力にクロックに同期して新しい状態を出力するフリップフロップです。
2進数と16進数
2進数は、2を基数として表した数です。0と1によってすべての数を表現します。また、2進1桁をビット(bit)といいます。
機械の内部では、電圧の高低を組み合わせて構成していますので、2進数の 0と1 を対応させることができます。
2進数は数値が大きくなるほど、桁数が大きくなり扱いにくいので、コンピューターなどの周出力表示の方法としては16進数がよく使われます。
16進数は、16を基数として表した数です。1桁を0~9、A、B、C、D、E、Fの16個の数値で表現します。
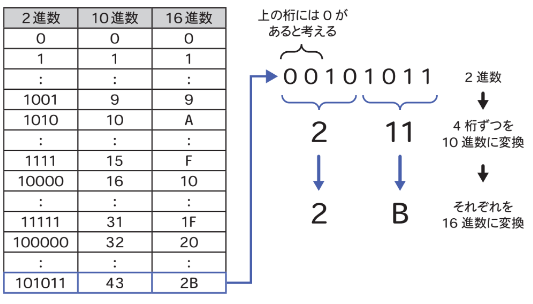
2進数と16進数の変換方法
2進数⇒16進数
- 2進数を4桁ずつに区切ります。桁が足りない場合は0を補います。
- 4桁ずつの2進数を10進数に変換します。
- 変換した10進数が10を超える場合は、該当するアルファベットに変換します。
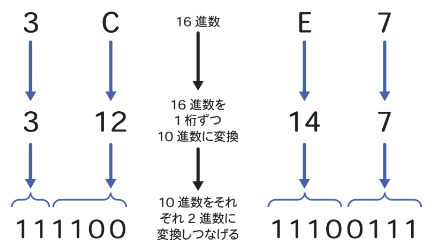
16進数⇒2進数
- 16進数を1桁ずつ10進数に変換します。
- 10進数をそれぞれ2進数に変換してつなげます。
電験三種-機械の過去問解説:論理回路とn進数
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問14
A-D変換器の入力電圧が 510[mV]のとき、2進数のディジタル量が (11111111)2 である。また、入力電圧が -510[mV]のとき、2進数のディジタル量が (00000000)2 である。アナログ量の入力電圧が 210[mV]のとき、2進数のディジタル量として、正しいのは次のうちどれか。
(1) (00110100)2 (2) (00110101)2 (3) (01001011)2 (4) (10001101)2 (5) (10110100)2
1997年(平成9年)問14 過去問解説
入力電圧が 510[mV]のとき、2進数のディジタル量が (11111111)2 であるので、10進数に変換すると、(255)10 になります。
入力電圧が -510[mV]のとき、2進数のディジタル量が (00000000)2 であるので、10進数に変換すると、(0)10 になります。
つまり、0~255の間を -510[mV]~510[mV]に目盛りがあることになります。1ビットが示す電圧は、
$\displaystyle\frac{510+510}{255}=4$[mV]
になります。アナログ量の入力電圧が 210[mV]を示すには、-510[mV]~210[mV]に 4 がいくつあるかということになりますので、
$\displaystyle\frac{210+510}{4}=180$[mV]
つまり、180目盛りとなりますので、これを 2進数に変換すると、(10110100)2 となります。

答え (5)
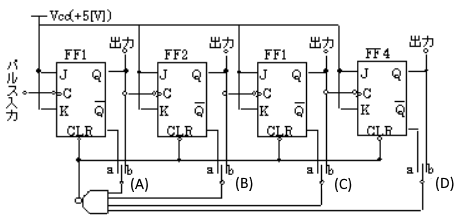
1998年(平成10年)問11
図の回路を非同期式10進カウンタ回路にするには、切替スイッチ(A),(B),(C)及び(D)をそれぞれa側,b側のどちら側に入れればよいか。正しいものを組み合わせたのは次のうちどれか。
| (A) | (B) | (C) | (D) | |
| (1) | b | b | b | a |
| (2) | b | a | b | b |
| (3) | a | a | b | a |
| (4) | a | b | a | b |
| (5) | a | a | a | b |
1998年(平成10年)問11 過去問解説
- 10進数は1~9までは一桁で次が二桁の10になる。例えば、8進数は1~7の次は10になる。
- FF(フリップフロップ)は入力が無い場合、正理論出力端子Qは0、負理論出力端子Qバーは1となる。
- この回路は、9までは一桁であるが、そのつぎの10になると、一桁目は0(二桁目は1になる。)になるので、FF1~FF3までの出力を全て0にしなければ(リセット)ならない。
- リセットをするための図下部にあるNAND回路の出力が0になるためには、入力の全てが1でなければならない。
- NAND回路入力の全てが1になるようにスイッチを選択する。
- (10)10=(1010)2、よって、2進数における1桁目は正理論で0なので、負理論は1になっている。したがって、負理論出力端子の$\bar{ Q}$(a)をNANDの入力の一つにする。
- 2進数における2桁目は正理論で1なので、負理論は0になっている。したがって、正理論出力端子のQ(b)をNANDの入力の一つにする。
- 2進数における3桁目は正理論で0なので、負理論は1になっている。したがって、負理論出力端子の$\bar{ Q}$(a)をNANDの入力の一つにする。
- 2進数における4桁目は正理論で1なので、負理論は0になっている。したがって、正理論出力端子のQ(b)をNANDの入力の一つにする。
答え (4)
1999年(平成11年)問11
図の回路で、入力として二つの2真数 A4A3A2A1=1110 及び B4B3B2B1=1001 を加え、切替スイッチSwをAに入れたとき、D4D3D2D1 は、( ア )であり、加算器の出力C0S4S3S2S1は( イ )となる。
また、切替スイッチSwをBに切り替えたとき、加算器出力 C0S4S3S2S1 は( ウ )となる。
上記の記述中の空白箇所(ア)、(イ)及び(ウ)に記入する数値として、正しいものを組み合わせたのは次のうちどれか。
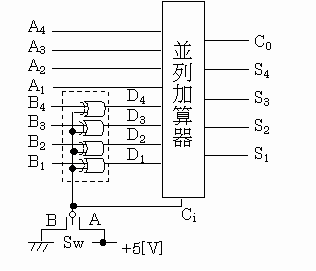
| (ア) | (イ) | (ウ) | |
| (1) | 0110 | 10101 | 10111 |
| (2) | 1001 | 10111 | 10100 |
| (3) | 0110 | 10101 | 10100 |
| (4) | 1001 | 10111 | 10111 |
| (5) | 0110 | 00101 | 10111 |
1999年(平成11年)問11 過去問解説
図記号は排他的論理和回路で、その真理値は入力が全て同じであれば、出力が 0 となり、入力が異なる値のものであれば、出力は 1 になります。
C1 は加算器の下位桁からの桁上がりの信号が入り、C0 は上位桁への桁上がりの信号が入ります。
SwをAに入れたとき
D1~D4の入力
B4B3B2B1=1001
+5Vの入力=1111
D4D3D2D1=0110・・・(ア)
加算器入力
D4D3D2D1=0110
A4A3A2A1=1110
C1=1
加算器出力
C0S4S3S2S1=10101・・・(イ)
SwをBに入れたとき
D1~D4の入力
B4B3B2B1=1001
0Vの入力=0000
D4D3D2D1=1001
加算器入力
D4D3D2D1=1001
A4A3A2A1=1110
C1=0
加算器出力
C0S4S3S2S1=10111・・・(ウ)
答え (1)
1999年(平成11年)問14
図1は論理回路とD-FFを組み合わせた回路である。いま入力信号AB及びとして、図2のタイムチャート(入力)に示す波形を加えたとき、出力信号Qの波形として、正しいのは図3のタイムチャート(出力)のうちどれか。
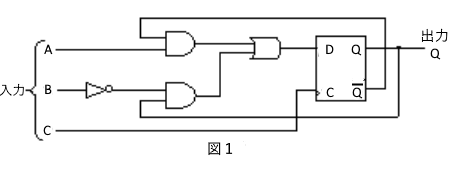
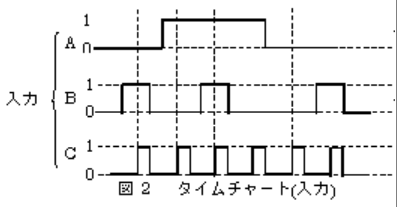
図3のタイムチャート(出力)
(1)

(2)
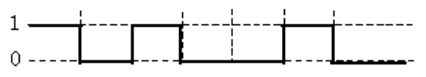
(3)
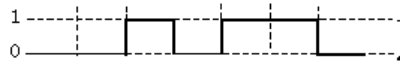
(4)
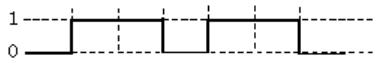
(5)

1999年(平成11年)問14 過去問解説
D-FFは、C(クロック)の入力が 0 から 1 になった時、そのときの D の入力信号をそのまま Q に出力します。その後、C が再び次の信号の 0 から 1 になるまで、D の入力信号がどのように変化しても、現在の Q の状態が保たれます。
- Q=1の場合
C の入力があると、$\bar{ Q}=0$ となりますが、B=1 のとき $\bar{ Q}=0$,Q=1 となります。A は、1でも0でもかまいません。 - Q=0の場合
A=1 のとき、C の入力があると、$\bar{ Q}=0$,Q=1となります。B は、1でも0でもかまいません。 - Cの入力がある。
上記三つの条件が重なったときの波形は(3)です。
答え (3)
2000年(平成12年)問11
入力信号がA、B及びC、出力信号がXの論理回路が次の真理値表を満たしているとき、Xの論理式として、正しいのは次のうちどれか。
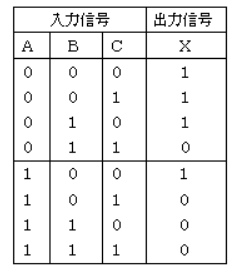
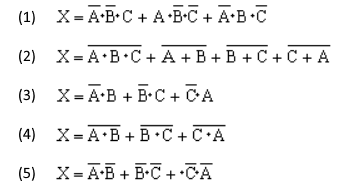
2000年(平成12年)問11 過去問解説
(1) (A,B,C)=(0,0,0)の場合
① X=0+0+0=0-該当せず。
② X=1+1+1+1=1
③ X=0+0+0=0-該当せず。
④ X=1+0+1=1
⑤ X=1+0+1=1
(2 ) (A,B,C)=(0,0,1)の場合
② X=1+1+0+1=1
④ X=1+1+1=1
⑤ X=1+1+1=1
(3) (A,B,C)=(0,1,0)の場合
② X=1+0+0+1=1
④ X=1+1+1=1
⑤ X=0+0+1=1
(4) (A,B,C)=(0,1,1)の場合
② X=0+0+0+0=0
④ X=1+0+1=1-該当せず。
⑤ X=0+0+0=0
(5) (A,B,C)=(1,0,0)の場合
② X=1+0+0+1=1
⑤ X=0+1+1=1
(6) (A,B,C)=(1,0,1)の場合
② X=1+0+0+0=1-該当せず。
⑤ X=0+0+0=0
答え (5)
2001年(平成13年)問11
16進数で“7FA9”と表現される2バイト(16ビット)のデータがある。このデータをアセンブラの回転命令により右へ3ビット回転したときの内容を16進数で表現した値として、正しいのは次のうちどれか。
ただし、右回転シフト命令は、キャリーフラグを含まず、16ビットのみを右回転するものとする。
(1) 0FF5 (2) 2FF5 (3) FD48 (4) FD4B (5) FFA8
2001年(平成13年)問11 過去問解説
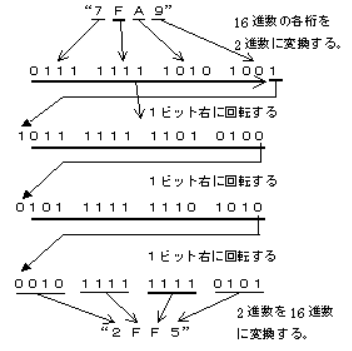
答え (2)
2001年(平成13年)問14
図1は①~④で示す発光ダイオード(LED)7個によるサイコロ表示パネルの配置図であり、図2は非同期式6進カウンタとデコーダを組み合わせてLED(サイコロの目)を点灯させる回路である。
図2において、リセットスイッチSを1回押した後、パルス入力端子に1個のパルスが加わるたびにLEDを表1の順序で点灯させる。
次の(a)及び(b)に答えよ。
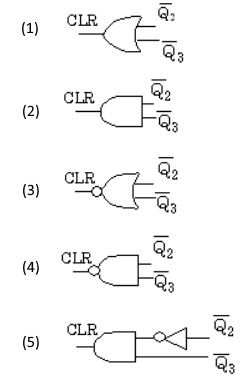
(a) 図2において、6進カウンタ信号をQ1、Q2、Q3に出力するようにしたい。図2中の論理回路(A)として、正しいのは次のうちどれか。
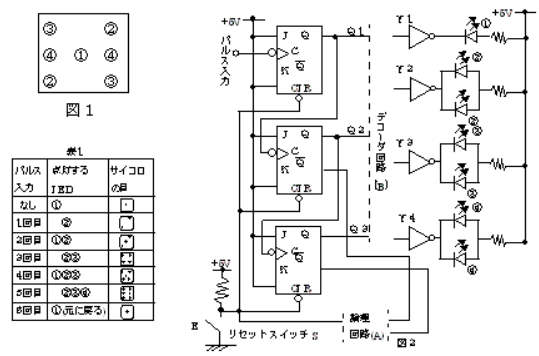
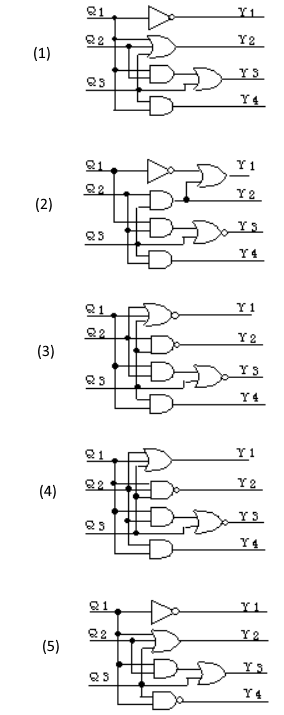
(b) LEDを表1の順序で点灯させたい。図2中のデコーダ回路(B)として、正しいのは次のうちどれか。
2001年(平成13年)問14 過去問解説
図1のJKフリップフロップは、2進1桁(0,1のビット)を記録するもので、カウンタ等の機能を持ちパルスの数を数えるものです。JとKは常にONで、Cにパルスが入力されれば、Qと$\bar{Q}$は、前の状態と反転(トルクモード)します。また、CLRにOFF(0)を入力すると、FFが0にクリアされて、QがOFF(0),$\bar{Q}$がON(1)となります。尚、”0″は0[V]、”1″は5[V]と考えます。
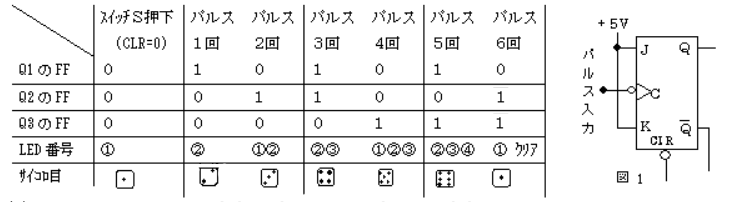
(a) $\overline{Q_2}$と$\overline{Q_3}$がともに “0”のとき、つまり$Q_2$と$Q_3$がともに”1″のとき、FFのCLRに”0″が加わりリセットとなります。サイコロの目の六が一になります。
答え (1)
(b) Y1,Y2,Y3,Y4に”1″入力時、そのLEDが点灯します。
答え (5)
2002年(平成14年)問11
図1のようなタイムチャートがある。図2の論理回路(ア)、(イ)、(ウ)、(エ)及び(オ)のうち、図1の動作を行うことができる回路が二つある。正しいものを組み合わせたのは次のうちどれか。
ただし、Yの初期値は0であるとする。
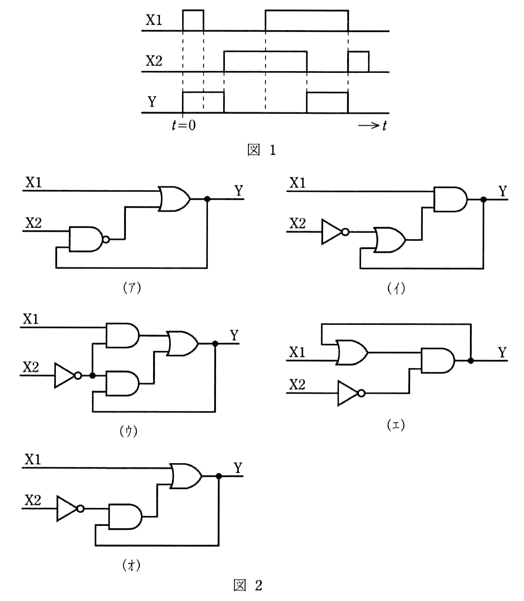
(1) (ア)と(イ) (2) (イ)と(ウ) (3) (ウ)と(エ) (4) (エ)と(オ) (5) (ア)と(オ)
2002年(平成14年)問11 過去問解説
(ア)~(オ)の論理回路を論理式で書き表します。(Y0:前回値,Y:今回値)
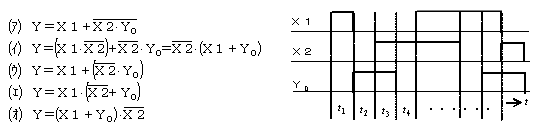
(ウ)と(エ)の真理値を調べます。
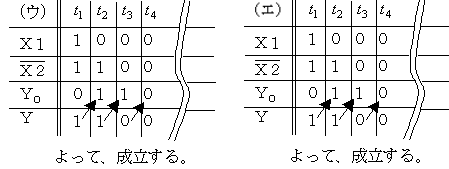
答え (3)
2003年(平成15年)問14
図のような論理回路において、入力A、B、Cに対する出力Xの論理式、及び入力をA=”0″、B=”1″、C=”1″としたときの出力Yの値として、正しいものを組合わせたのは次のうちどれか。
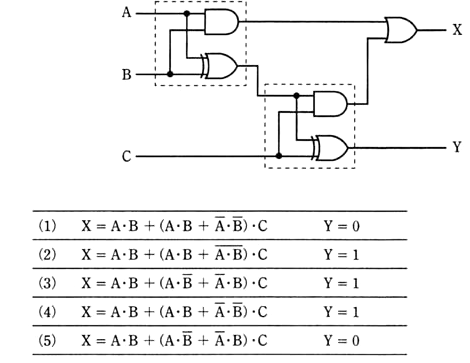
2003年(平成15年)問14 過去問解説
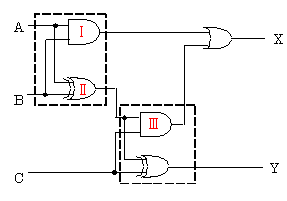

答え (5)
2004年(平成16年)問14
計算機に用いる数に関する記述として、誤っているのは次のうちどれか。
- 2進数の(1101)2を10進数に変換すると(13)10になる。
- 10進数の(23)10を2進数に変換すると(10111)2になる。
- 10進数の(23)10を2進化10進数に変換すると(00100011)2になる。
- 2進数の(1101)2を16進数に変換すると(D)16になる。
- 16進数の(C3)16を10進数に変換すると(123)10になる。
2004年(平成16年)問14 過去問解説
- (1101)2=1×23+1×22+0×21+1×20=8+4+1=(13)10
- (10111)2=1×24+0×23+1×22+1×21+1×20=16+4+2+1=(23)10
- (00100011)2進化10進数=(23)10
- (1101)2=(13)10=(D)16
- (C3)16=(12×161+3×160)10=(192+3)10=(195)10
答え (5)
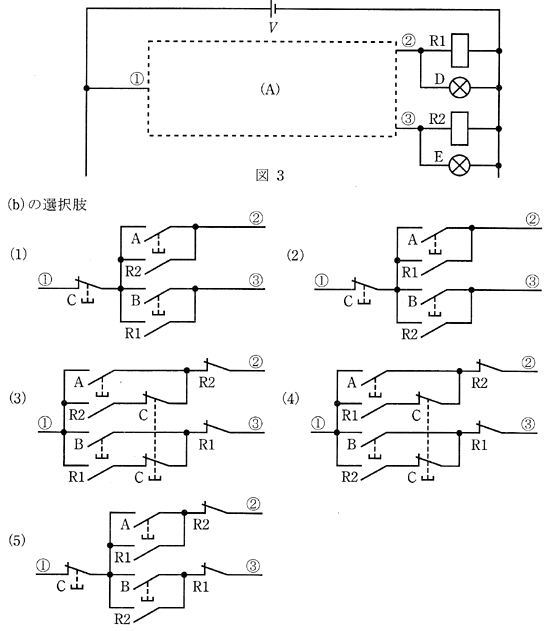
2004年(平成16年)問18
図1の論理回路の動作を表わすタイムチャートが図2がある。図3と図1と同じ働きをするリレーシーケンス回路である。次の(a)及び(b)に答えよ。
(a) 図1の回路において、スイッチA,B,Cに図2の入力スイッチA,B,C信号を加えたとき、LED出力Dの出力信号を図2の出力D信号(ア)、(イ)又は(ウ)より選び、また、LED出力Eの出力信号を図2の出力E信号(エ)、(オ)又は(カ)より選ぶとすれば、その正しい組合せたのは次のうちどれか。
ただし、スイッチCはリセット信号であり、出力D及びEの初期値は”0″であるとする。
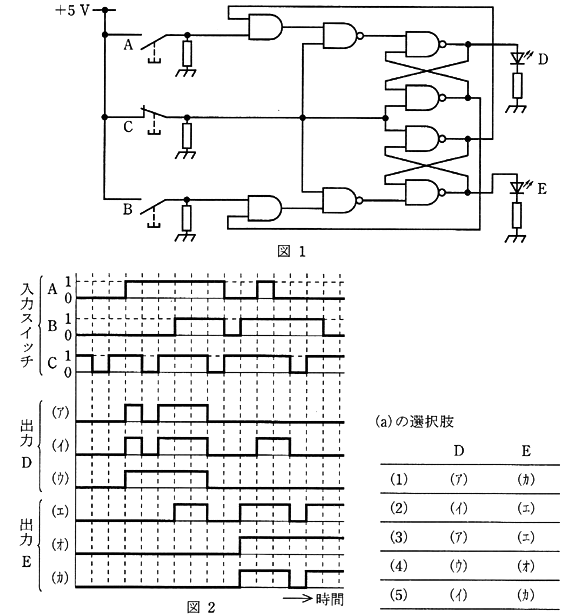

2004年(平成16年)問18 過去問解説
(a) 回路の動作説明
- Cが0のとき、リセットになって、D,E共に0となる。
- Dが1になるためには、E側のFF(フリップ・フロップ)がリセットになっていなければならない。
- Aが1になると、A側のFFがセットされる。
- Bが1になると、B側のFFがセットされる。
- 先にセットされたFFは、その後で他方のスイッチが1になっても、後で1になったスイッチ側のFFはセットされない。
- Aが1、Bが0で、Cが1のとき、直前の状態を保持する。
図2のタイムチャートのタイミングの「マス」を左から順にT1,T2,T2,・・・・とする。

ー:前の状態を保持する。
答え (1)
(b) 図1の回路において、スイッチCが0のとき、回路はリセットされるので、スイッチCは他の回路と直列に接続されることになる。
また、スイッチAがセットの場合、A側のFFがセットされるので、R1とスイッチAは直列でなければならない。したがって、スイッチBにおいても同様でなければならない。
答え (5)
2005年(平成17年)問14
図のように、入力A,B及びC、出力Xの論理回路がある。Xを示す論理回路として、正しいのは次のうちどれか。
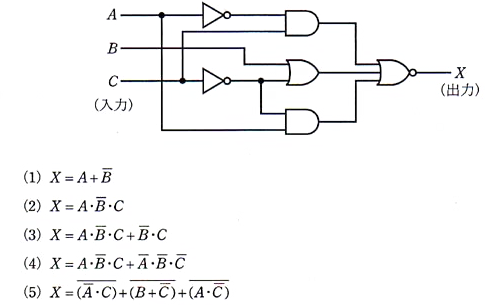
2005年(平成17年)問14 過去問解説
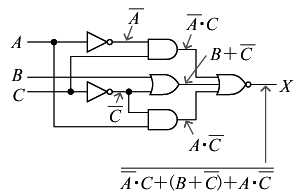
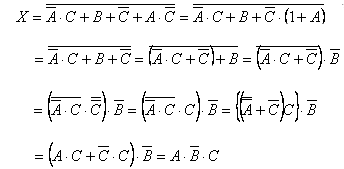
答え (2)
2006年(平成18年)問14
入力信号A、B及びC、出力信号Xの論理回路の真理値表が次のように示されたとき、Xの論理式として、正しいのは次のうちどれか。
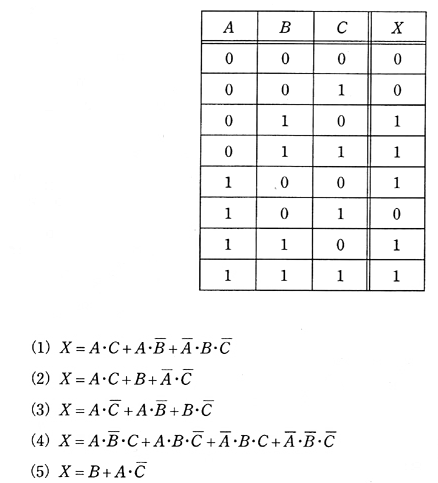
2006年(平成18年)問14 過去問解説
Xが1のときのABCの論理積を求めます。
0 1 0 1 → $\bar{A}・B・\bar{C}$
0 1 1 1 → $\bar{A}・B・C$
1 0 0 1 → $A・\bar{B}・\bar{C}$
1 1 0 1 → $A・B・\bar{C}$
1 1 1 1 → $A・B・C$
$X=\bar{A}・B・\bar{C} + \bar{A}・B・C + A・\bar{B}・\bar{C} + A・B・\bar{C} + A・B・C$
$=\bar{A}・B(\bar{C}+C)+A・\bar{B}・\bar{C}+A・B(\bar{C}+C)$
$=\bar{A}・B+A・\bar{B}・\bar{C}+A・B$
$=\bar{A}・B+A(B+\bar{B}・\bar{C})$
$=\bar{A}・B+A(B+\bar{C})$
$=B(\bar{A}+A)+A\bar{C}$
$=B+A\bar{C}$
答え (5)
2006年(平成18年)問18
フリップフロップを含む回路を考える。その入力は、手動式パルス発生回路からの信号パルスである。次の(a)及び(b)に答えよ。
(a) 手動式パルス発生回路において、有接点スイッチSWを切り換えてパルスを発生させると、出力信号にチャタリングが発生する場合がある。そのため、手動式パルス発生回路にはチャタリング防止回路が必要になる。
図A、図B、図C及び図Dが示す回路のうち、スイッチの切り換えによるチャタリングが出力に出ないパルス発生回路は二つある。その二つは下記の選択肢のうちどれか。
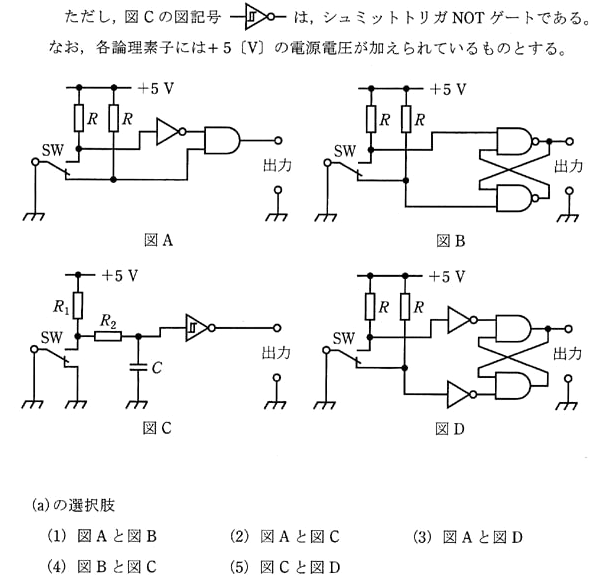
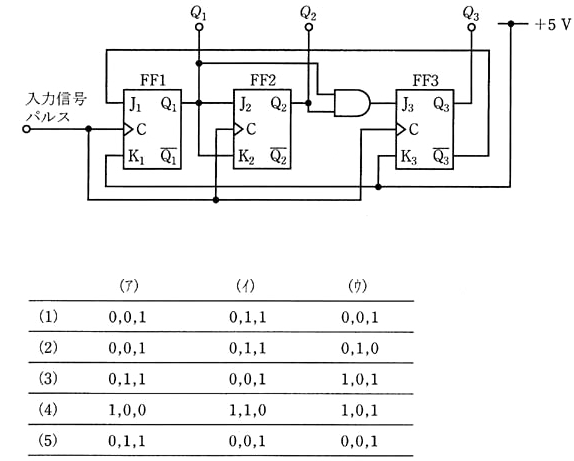
(b) フリップフロップを含む回路として、図に示すように3個のJK-FF(JK-フリップフロップ)を考える。入力信号パルスはJK-FFの各C端子に同時に加わり、JK-FFの出力(Q3、Q2、Q1)に信号が現れる。JK-FFは初期状態において、出力(Q3、Q2、Q1)の値は(0、0、0)2であるとする。
図の回路に一つめの入力信号パルスが加わると、そのとき(J3、J2、J1)の値は( ア )2になる。また、二つめの入力信号パルスが加わると、そのとき、(J3、J2、J1)の値は、( イ )2になる。
以下、三つめ、四つめの入力信号パルスが加わり、五つめの入力信号パルスが加わった後の(J3、J2、J1)の値は、( ウ )2になる。
上記の記述中の空欄箇所(ア)、(イ)及び(ウ)に当てはまる論理値として、正しいものを組み合わせたのは次のうちどれか。
2006年(平成18年)問18 過去問解説
(a) 図BはSR-FFを用いたチャタリング防止回路であり、図CはシュミットトリガーNOTゲートを用いたチャタリング防止回路です。
答え (4)
(b) (Q3,Q2,Q1)=(0,0,0)のとき、(J1,k1)=(1,1)で、(J3,J2,J1)=(0,0,1)になっています。
一つ目のパルスが入力されると、FF1はトグル動作でQ1は0から1になります。FF2は、(J2,k2)=(0,1)の状態でパルスが入るから、Q2の0に変化は無く、0です。Q2が0であれば、FF3のJ3も0が維持されて、(J3,J2,J1)=(0,1,1)となります。
二つ目のパルスが入力されると、FF1のQ1は1から0に変わり、FF2のQ2は0から1に変わります。FF3のQ3に変化はなく、(J3,J2,J1)=(0,0,1)となります。
三つ目のパルスがはいると、同種の動作を繰り返して(J3,J2,J1)=(0,0,1)となります。
答え (5)
2007年(平成19年)問14
図に示す論理回路において、入力A及びBの論理レベルと、出力Xの論理レベルの関係を表わしている正しい真理値表は次のうちどれか。
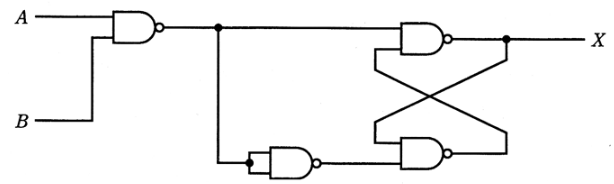
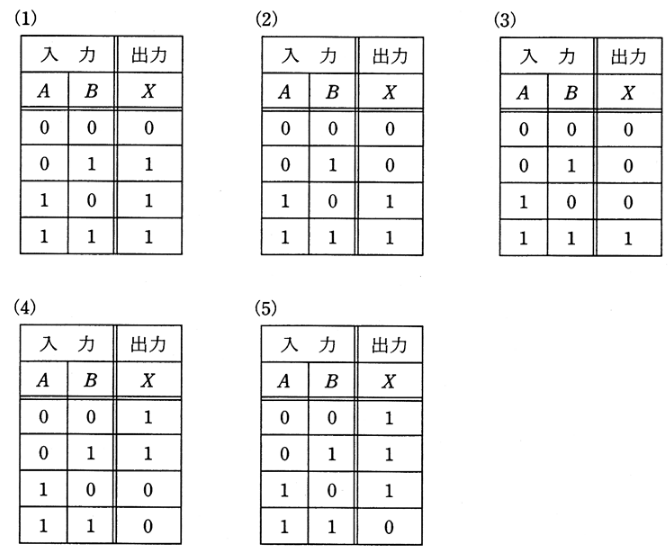
2007年(平成19年)問14 過去問解説
RSフリップフロップは、二つの入力信号によって、その出力状態をリセット(Reset)された状態またはセット(Set)された状態に保持します。
NAND回路は、入力信号が両方1のとき出力が0で、それ以外は出力は1になります。
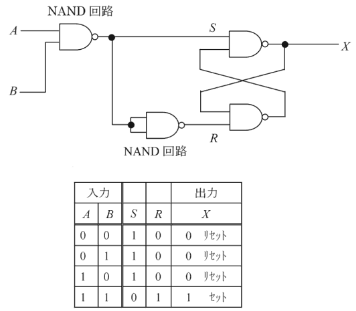
答え (3)
2009年(平成21年)問14
2進数A,Bが、A=(1100 0011)2,B=(1010 0101)2であるとき、AとBのビットごとの論理演算を考える。AとBの論理積(AND)を16進数で表すと( ア )、AとBの論理和(OR)を16進数で表すと( イ )、AとBの排他的論理和(EX-OR)を16進数で表すと( ウ )、AとBの否定的論題積(NAND)を16進数で表すと( エ )となる。
上記の記述中の空白箇所(ア),(イ),(ウ)及(エ)に当てはまる数値として,正しいものを組み合わせたのは次のうちどれか。

2009年(平成21年)問14 過去問解説

答え (2)
2009年(平成21年)問18
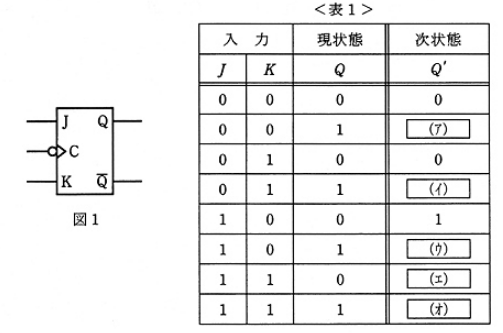
JK-FF(JK-フリップフロップ)の動作とそれを用いた回路について、次の(a)及び(b)に答えよ。
(a) 図1のJK-FF の状態遷移について考える。JK-FF のJ ,Kの入力時における出力をQ (現状態)、J ,K の入力とクロックパルスの立下がりによって変化するQ の変化後の状態(次状態)の出力を Q’として、その状態遷移を表 1 のようにまとめる。表 1 中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる真理値として、正しいものを組み合わせたのは次のうちどれか。

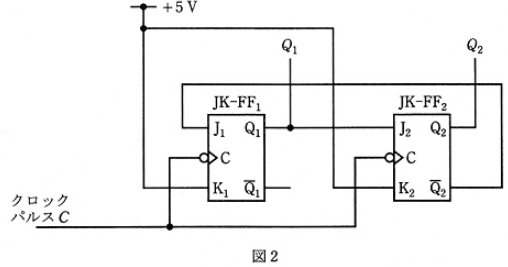
(b) 2個のJK-FFを用いた図2の回路を考える。この回路において、+5[V]を”1”,0[V]を”0”と考えたとき、クロックパルスCに対する回路の出力Q1及びQ2のタイムチャートとして、正しいのは次のうちどれか。
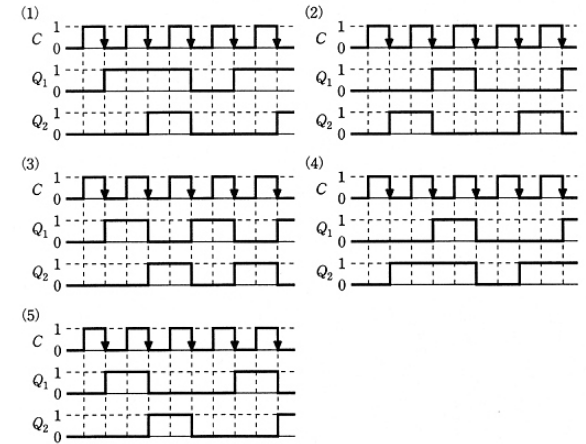
2009年(平成21年)問18 過去問解説
(a) 入力端子JとKの状態の組み合わせにより、出力にクロックに同期して新しい状態を出力するフリップフロップです。クロックパルスが立下がった時、状態を変化させることができます。
J=K=0 のときは前の状態を保持し、J=K=1 のときは反転します。
答え (4)
(b) 初期状態C=0から順次動作を追っていきます。
初期状態
JK-FF1:J1=1, K1=1
JK-FF2:J2=0 ,K2=1
1回目のC の立下り
JK-FF1(反転):J1=1,K1=1,Q1=1
JK-FF2(保持):J2=1,K2=1,Q2=0
2回目のC の立下り
JK-FF1(反転):J1=0,K1=1,Q1=0
JK-FF2(反転):J2=0,K2=1,Q2=1
(5)のタイムチャートとなります。
答え (5)
2010年(平成22年)問14
入力信号がA,B及びC、出力信号がXの論理回路として、次の真理値表を満たす論理回路は次のうちどれか。
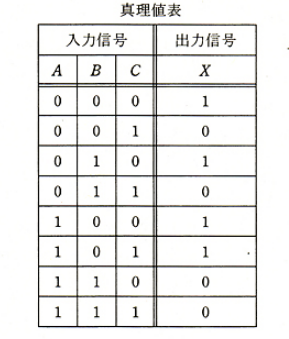
2010年(平成22年)問14 過去問解説
真理値表の論理式は次のようになります。
$X=\bar{A}・\bar{B}・\bar{C} + \bar{A}・B・\bar{C}+ A・\bar{B}・\bar{C} + A・\bar{B}・C$
$=\bar{A}・\bar{C} ( \bar{B}+B)+ A・\bar{B}(\bar{C} +C)$
$=\bar{A}・\bar{C} + A・\bar{B}$
$=\overline{A+C}+ A・\bar{B}$
この式を満たす回路は(2)となります。
答え (2)
2010年(平成22年)問18
数の表現法について、次の(a)及び(b)に答えよ。
(a) 10 進法で表される正の整数 N は、10 進法の 2 以上の整数 r を用いて、次式のように
表すことができる。
N=anrn+an-1rn-1+…+a1r+a0
ただし、aiは整数であり、0≦ai<r(i=0,1,…,n)のである。
このとき、N を r 進法で次のように表現することとする。
(anan-1…a2a1a0)r
この表現方法によって次の計算が成り立っとき、r の値として正しいのは次のうちどれか。
(122)r-(42)r=(40)r
(1)5 (2)6 (3)7 (4)8 (5)9
(b)8 ビットの固定長で、正負のある 2 進法の数値を表現する場合、次のような①及び②で示す方式がある。また、D-A コンバータにおいては次の③で示す方式が用いられる。
① 最上位ビット(左端のビット、以下 MSB という)を符号ビットとして、残りのビットでその数の絶対値を表す方式は、絶対値表示方式と呼ばれる。この場合、MSB=0 が正(+)、MSB=1 が負(-)と約束すると、10 進数の-8 は ( ア ) となる。
② 7 ビット長で表された正の数 n に対して、-n を 8 ビット長の n の 2 の補数で表す方式がある。この方式による場合、10 進数の-8 は ( イ ) となる。この方式においても、MSB=1 は負の整数、MSB=0 は正の整数を示すことになる。この方式は、2 進数の減算に適している。
③ D-A コンバータでは、ディジタル入力量とアナログ出力量が比例の関係にある。8 ビットの D-A コンバータではディジタル入力量として、(1000 0000)2 を与えた場合に、0.0000〔V〕が出力されるようにしたオフセット・バイナリ・コードを用いることが多い。この場合、出力電圧が正のときは、MSB=1 となり、負のときは、MSB=0 となる。
ディジタル入力値が(0000 0000)2のときのアナログ出力値が-5.0000[V]であるオフセ
ット・バイナリ・コードの D-A コンバータでは、ディジタル入力値が(0111 1000)2 のときの出力電圧値は ( ウ ) [V]となる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる数値として、正しいもの
を組み合わせたのは次のうちどれか。

2010年(平成22年)問18 過去問解説
(a) 与えられた表現方法を数式にすると下記となります。
1×r2+2r+2-(4r+2)=4r
r(r-6)=0
r=6
答え (2)
(b) D-A コンバータの入出力の関係を図で表します。
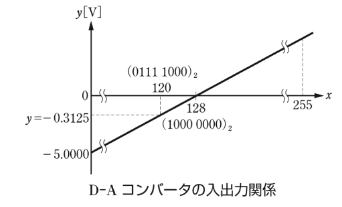
① 最上位ビット(左端のビット、以下 MSB という)を符号ビットとして、残りのビットでその数の絶対値を表す方式は、絶対値表示方式と呼ばれる。この場合、MSB=0 が正(+)、MSB=1 が負(-)と約束すると、10 進数の-8 は ( (1000 1000)2 ) となる。
② 7 ビット長で表された正の数 n に対して、-n を 8 ビット長の n の 2 の補数で表す方式がある。この方式による場合、10 進数の-8 は ( (1111 1000)2 ) となる。この方式においても、MSB=1 は負の整数、MSB=0 は正の整数を示すことになる。この方式は、2 進数の減算に適している。
③ D-A コンバータでは、ディジタル入力量とアナログ出力量が比例の関係にある。8 ビットの D-A コンバータではディジタル入力量として、(1000 0000)2 を与えた場合に、0.0000〔V〕が出力されるようにしたオフセット・バイナリ・コードを用いることが多い。この場合、出力電圧が正のときは、MSB=1 となり、負のときは、MSB=0 となる。
ディジタル入力値が(0000 0000)2のときのアナログ出力値が-5.0000[V]であるオフセ
ット・バイナリ・コードの D-A コンバータでは、ディジタル入力値が(0111 1000)2 のときの出力電圧値は ( -0.3125 ) [V]となる。
答え (3)
2011年(平成23年)問14
図のように、入力信号A,B及びC,出力信号Zの論理回路がある。この論理回路の真理値表として正しいものを次の(1)~(5)のうちから一つ選べ。
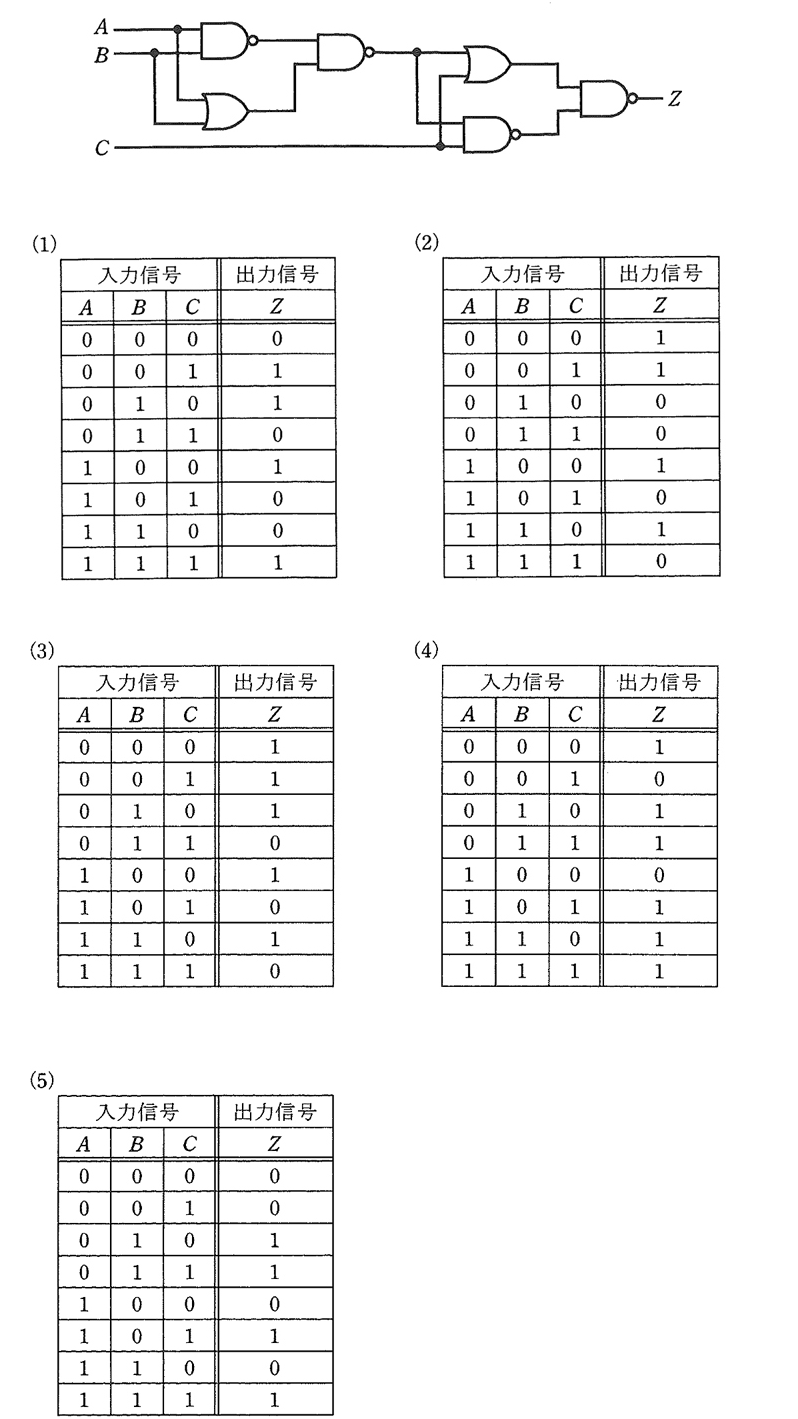
2011年(平成23年)問14 過去問解説
試しに、A=0,B=0,C=0 として、論理回路に当てはめます。
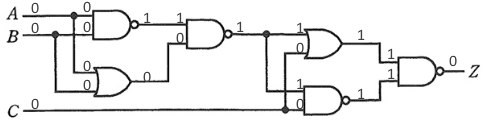
z=0 となりますので、該当するのは(1)か(5)の真理値表です。
次に、A=0,B=0,C=1 として、論理回路に当てはめます。
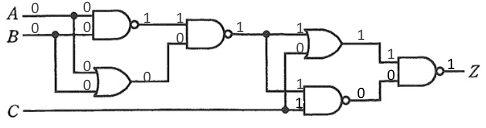
z=0 となりますので、該当するのは(1)の真理値表です。
答え (1)
2011年(平成23年)問18
次のカルノー図から得られた結果Xは次式の論理式で示される。
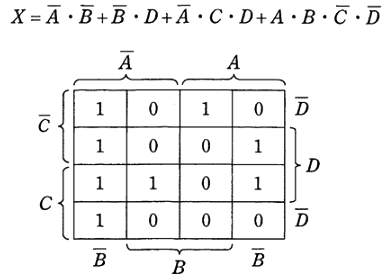
次の(a)及び(b)の問に答えよ。
(a) Xの式をNAND回路及びNOT回路で表現する論理式として、正しいものを次の(1)~(5)のうちから一つ選べ。
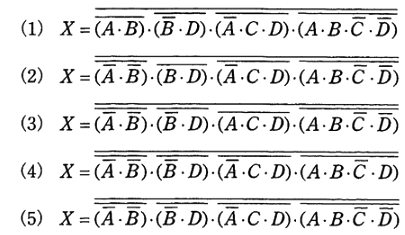
(b) Xの式をNOR回路及びNOT回路で表現する論理式として、正しいものを次の(1)~(5)のうちから一つ選べ。
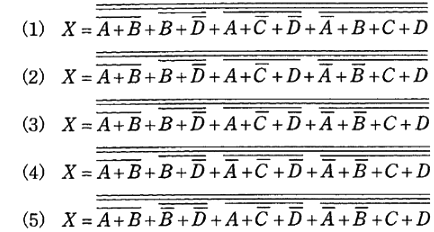
2011年(平成23年)問18 過去問解説
(a) 論理式Xを、ド・モルガンの定理を使ってNAND回路及びNOT回路で実現する式に変形します。
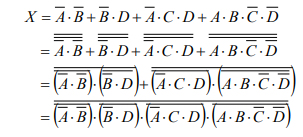
答え (5)
(B) 論理式Xを、ド・モルガンの定理を使ってNOR回路及びNOT回路で実現する式に変形します。
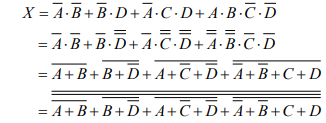
答え (3)
2012年(平成24年)問14
図のような論理回路において、入力 A、B 及び C に対する出力 X の論理式、並びに入力を A=0、B=1、C=1としたときの出力 Y の値として、正しい組合せを次の(1)~(5)のうちから一つ選べ。
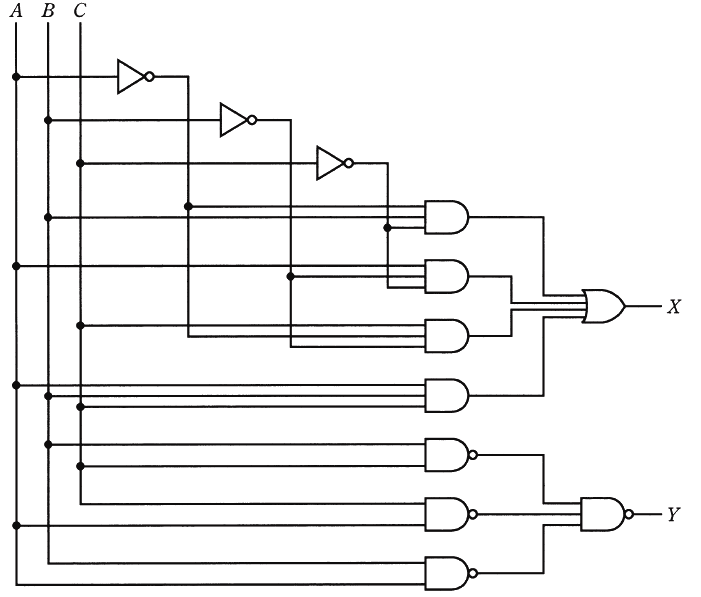
2012年(平成24年)問14 過去問解説
A=0,B=1,C=1 、論理回路に当てはめます。
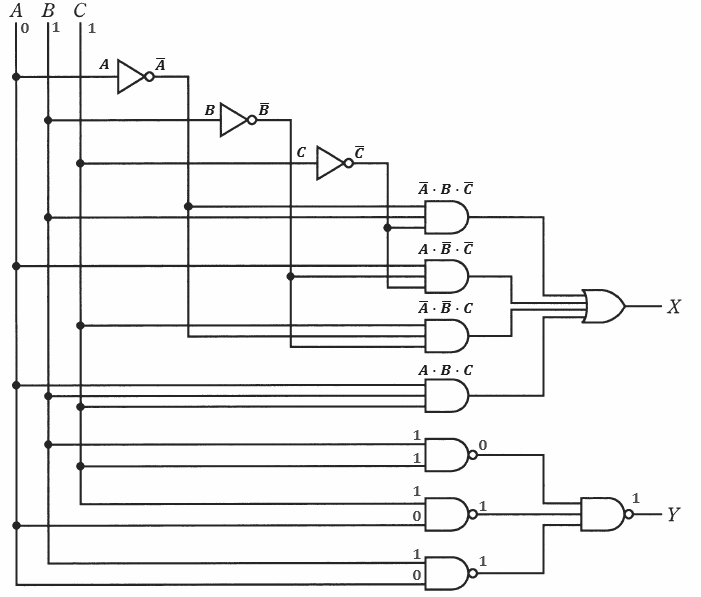
図より、
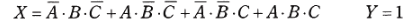
答え (1)
2013年(平成25年)問14
図の論理回路に、図に示す入力A、B及びCを加えたとき、出力Xとして正しいものを次の(1)~(5)のうちから一つ選べ。
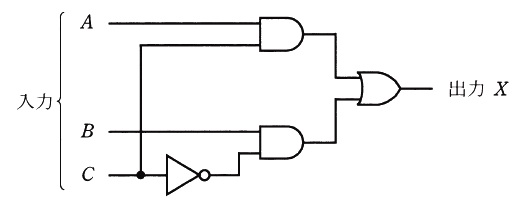
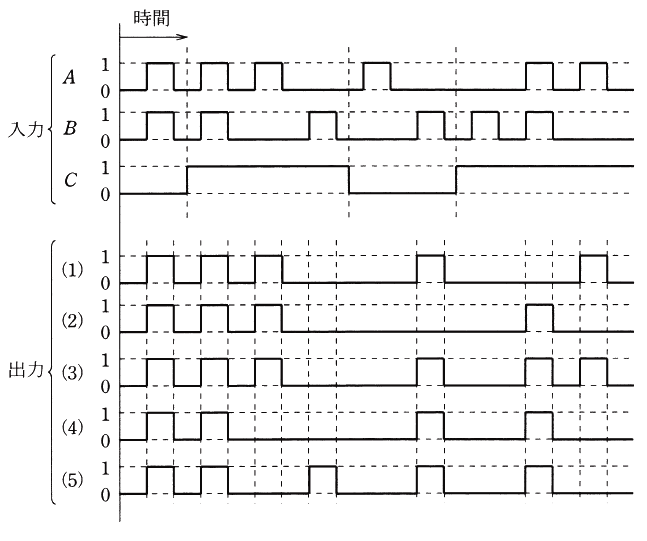
2013年(平成25年)問14 過去問解説
消去法で考えます。まず、出力に違いがある①の時間に注目して、A=1,B=0,C=1 を論理回路に当てはめます。
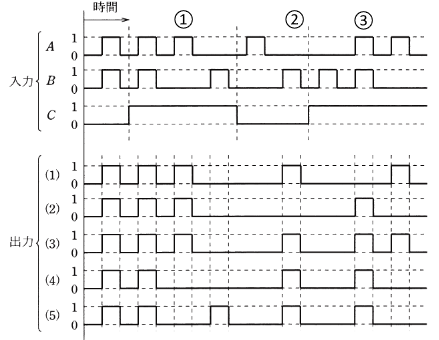
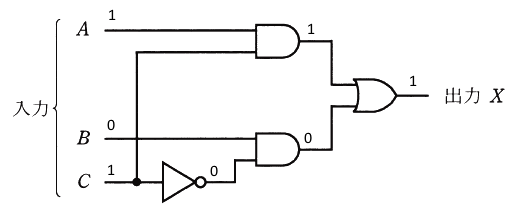
X=1 となりますので、該当するのは(1),(2),(3)のタイムチャートです。
次に、②の時間に注目して、A=0,B=1,C=0 を論理回路に当てはめます。
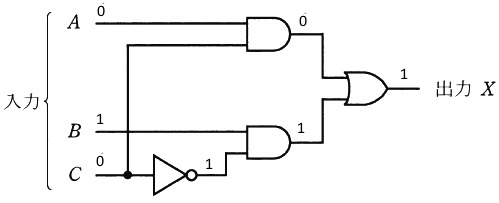
X=1 となりますので、該当するのは(1),(3)のタイムチャートです。
次に、③の時間に注目して、A=1,B=1,C=1 を論理回路に当てはめます。
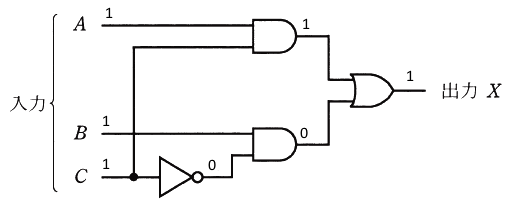
X=1 となりますので、該当するのは(3)のタイムチャートです。
答え (3)
2013年(平成25年)問18
論理関数に関する次の(a)及び(b)の問に答えよ。
(a) 論理式
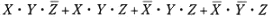
を積和形式で簡単化したものを次の(1)~(5)のうちから一つ選べ。
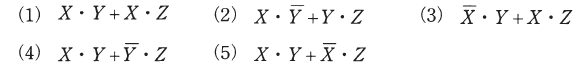
(b) 論理式
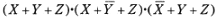
を和積形式で簡単化したものを次の(1)~(5)のうちから一つ選べ。
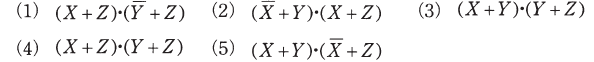
2013年(平成25年)問18 過去問解説
(a)の解答
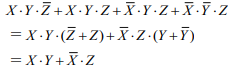
答え (5)
(b)の解答
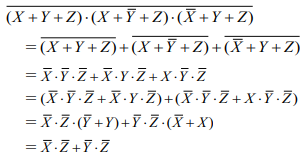
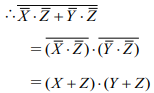
答え (4)
2014年(平成26年)問18
図はJK-フリップフロップ(FF1、FF2、FF3)と論理回路Dを用いた非同期式カウンタ回路とそのタイムチャートである。次の(a)及び(b)の問に答えよ。
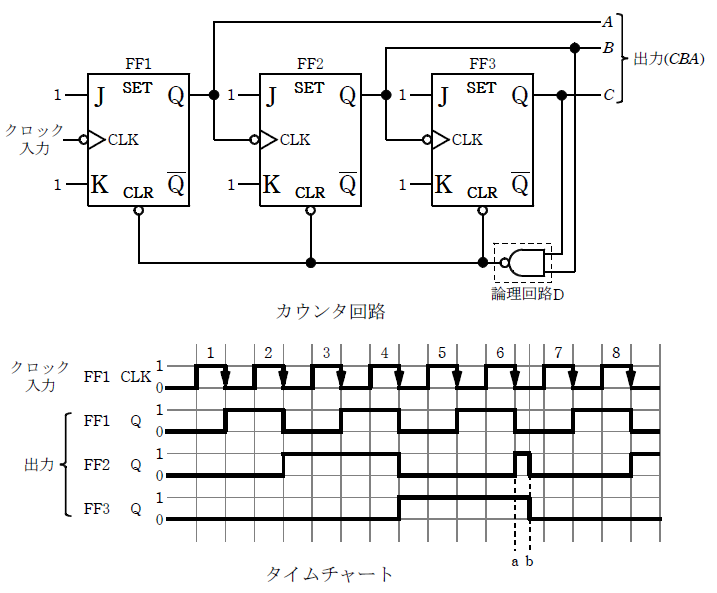
(a) カウンタ回路における論理回路Dは、( ア )回路で、その役割は出力(CBA)が2進数でカウンタの最大数( イ )になった後、次のクロック入力の立ち下がりによって出力(CBA)を2進数で( ウ )にすることである。
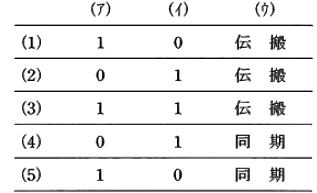
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
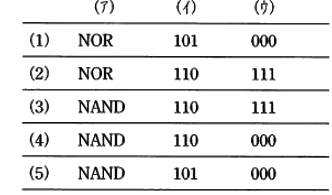
(b) タイムチャートにおいて、クロック入力のパルス6の立ち下がりでFF1のQ出力は1から0へ変化する。FF1の立ち下がりはFF2を動作させ、0から1に変化させる。図のa時点でFF2及びFF3のQ出力はともに( ア )である。
これら二つの( ア )は論理回路Dに入力され、その出力は( イ )となる。この( イ )は三つのJK-フリップフロップのCLR入力端子に入って、b時点において、クリアされている。
a時点からb時点までのFF2のQに現われるパルスは、パルス幅が非常に狭いため、カウンタの出力( ア )としてはカウントされない。カウンタは再びカウントを開始する。
クロック入力のパルス6が1から0に変化する時刻と、FF2及びFF3が最終的にb時点でクリアされる時刻とには時間遅れが生じている。これは論理回路Dとフリップフロップの入出力における信号の( ウ )遅れに起因している。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
2014年(平成26年)問18 過去問解説
(a) カウンタ回路における論理回路Dは、( NAND )回路で、その役割は出力(CBA)が2進数でカウンタの最大数( 101 )になった後、次のクロック入力の立ち下がりによって出力(CBA)を2進数で( 000 )にすることである。
答え (5)
(b) タイムチャートにおいて、クロック入力のパルス6の立ち下がりでFF1のQ出力は1から0へ変化する。FF1の立ち下がりはFF2を動作させ、0から1に変化させる。図のa時点でFF2及びFF3のQ出力はともに( 1 )である。
これら二つの( 1 )は論理回路Dに入力され、その出力は( 0 )となる。この( 0 )は三つのJK-フリップフロップのCLR入力端子に入って、b時点において、クリアされている。
a時点からb時点までのFF2のQに現われるパルスは、パルス幅が非常に狭いため、カウンタの出力( 1 )としてはカウントされない。カウンタは再びカウントを開始する。
クロック入力のパルス6が1から0に変化する時刻と、FF2及びFF3が最終的にb時点でクリアされる時刻とには時間遅れが生じている。これは論理回路Dとフリップフロップの入出力における信号の( 伝搬 )遅れに起因している。
答え (1)
2015年(平成27年)問14
次の真理値表の出力を表す論理式として、正しい式を次の(1)~(5)のうちから一つ選べ。
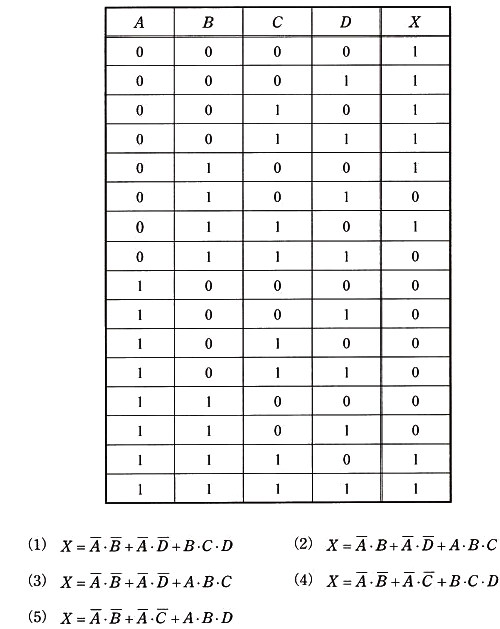
2015年(平成27年)問14 過去問解説
真理値表で X=1 となる論理式の論理和を求めます。
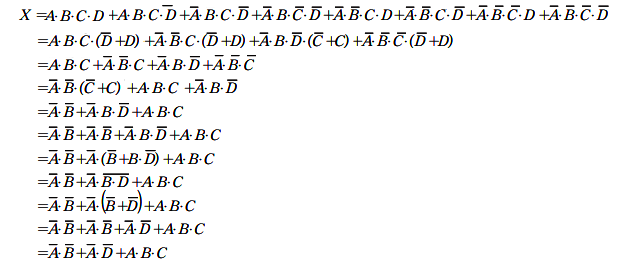
答え (3)
2016年(平成28年)問14
次の文章は、基数の変換に関する記述である。
- 2進数00100100を10進数で表現すると( ア )である。
- 10進数170を2進数で表現すると( イ )である。
- 2進数111011100001を8進数で表現すると( ウ )である。
- 16進数( エ )を2進数で表現すると11010111である。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
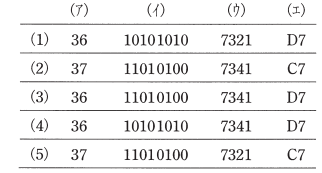
2016年(平成28年)問14 過去問解説
(ア) 2進数から10進数への変換は、 1 が立っているところに2のベキ乗をかけて足し合わせます。
(00100100)2=0×27+0×26+1×25+0×24+0×23+1×22+0×21+0×20
=0×128+0×64+1×32+0×16+0×8+1×4+0×2+0×1
=0+0+32+0+0+4+0+0=36
(イ) 10進数から2進数への変換は、与えられた数を2で割っていき、余りを下から書いていくことで変換できます。
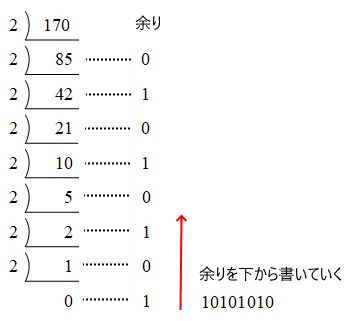
(ウ) 2進数から8進数への変換は、下位ビットより3桁ずつに区切り10進に変換します。
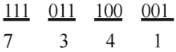
(エ) 2進数から16進数への変換は、下位ビットより4桁ずつに区切り16進に変換します。
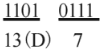
答え (4)
2016年(平成28年)問18 過去問解説
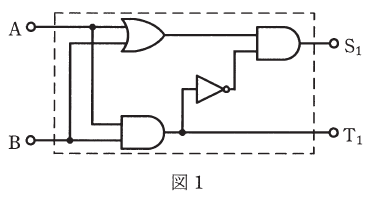
次の論理回路について、(a)及び(b)の問に答えよ。
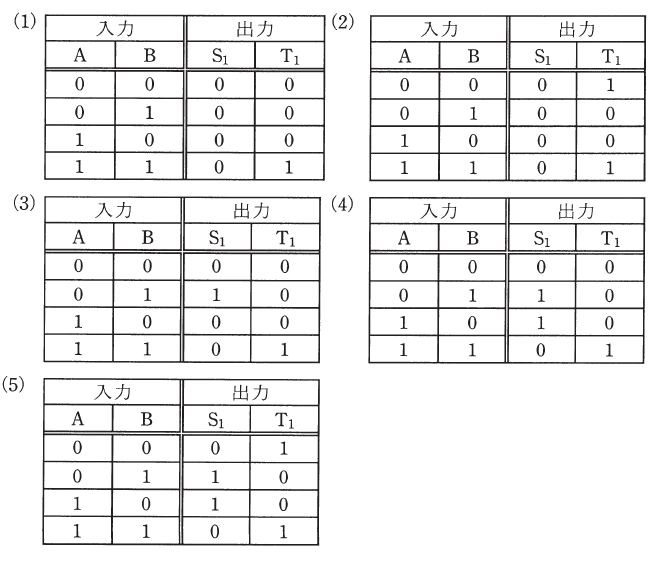
(a) 図1に示す論理回路の真理値表として、正しいものを次の(1)~(5)のうちから一つ選べ。
(b) 図1に示す論理回路を2組用いて図2に示すように接続して構成したとき、A、B及びCの入力に対する出力S2及びT2の記述として、正しいものを次の(1)~(5)のうちから一つ選べ。
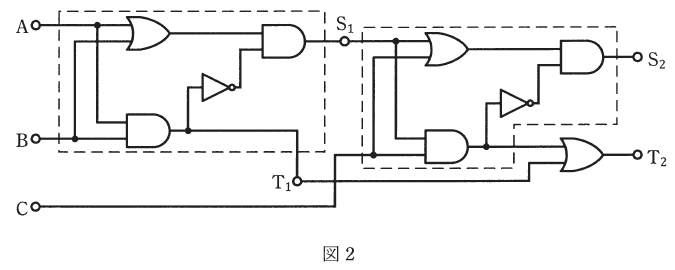
- A=0、B=0、C=0を入力したときの出力は、S2=0、T2=1である。
- A=0、B=0、C=1を入力したときの出力は、S2=0、T2=1である。
- A=0、B=1、C=0を入力したときの出力は、S2=1、T2=0である。
- A=1、B=0、C=1を入力したときの出力は、S2=1、T2=0である。
- A=1、B=1、C=0を入力したときの出力は、S2=1、T2=1である。
2016年(平成28年)問18 過去問解説
(a) 論理回路に数値を当てはめます。
A=0、B=0 のとき
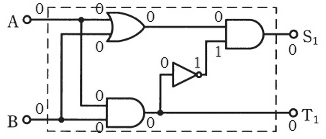
A=0、B=1 のとき
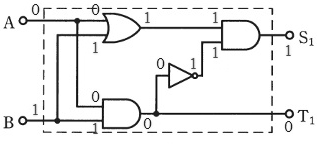
A=1、B=0 のとき
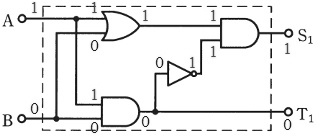
A=1、B=1 のとき
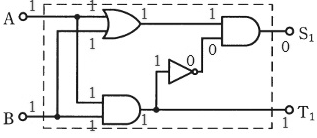
答え (4)
(b) 問(a)と同じように、論理回路に(1)~(5)の数値を当てはめます。
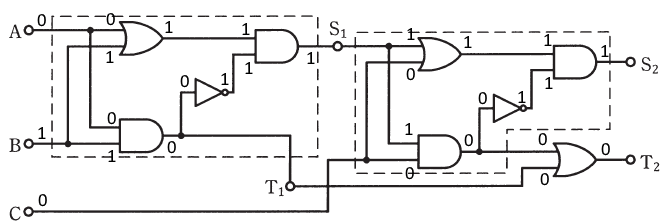
答え (3)
2017年(平成29年)問14
二つのビットパターン1011と0101のビットごとの論理演算を行う。排他的論理和(ExOR)は( ア )、否定論理和(NOR)は( イ )であり、( ア )と( イ )との論理和(OR)は( ウ )である。0101と( ウ )との排他的論理和(ExOR)の結果を2進数と考え、その数値を16進数で表すと( エ )である。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

2017年(平成29年)問14 過去問解説
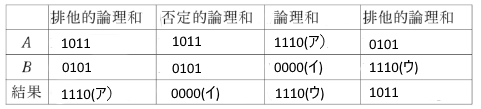
1011を16 進数へ変換すると、
1×23+0×22+1×21+1×20=(11)10=(B)16 … (エ)
答え (5)






