第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「変圧器の等価回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「変圧器の等価回路」の過去問題も解説しています。
変圧器の等価回路とベクトル図
理想変圧器
巻線に発生する抵抗損や漏れ磁束による漏れリアクタンスなどが全く無く、一次側の電圧電流を全て二次側に変圧変流することのできる変圧器のことを「理想変圧器」といいます。
実際の変圧器には、巻線に発生する抵抗損や漏れ磁束による漏れリアクタンスがあります。それらの損失を変圧器から切り離して、理想変圧器の外部に、一次・二次巻線の抵抗 $r_1$[Ω],$r_2$[Ω]、漏れリアクタンス $x_1$[Ω],$x_2$[Ω]を接続した等価回路は、図1のように考えることができます。
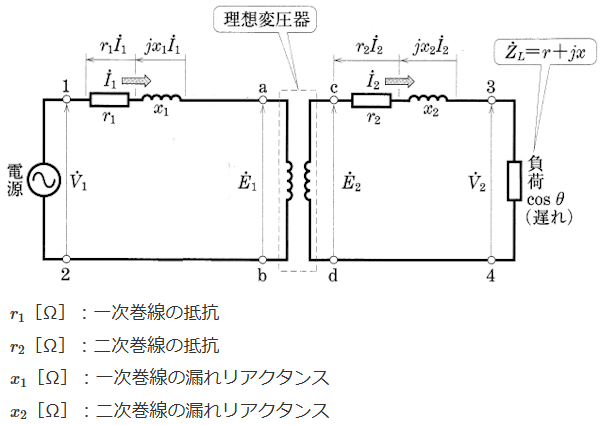
コイルに電流を流すとコイルの中に磁束が発生します。この時コイルの外にも磁束は発生しています。このコイルの外に発生する磁束を漏れ磁束といいます。このとき、漏れ磁束によりコイルに誘導性リアクタンスが発生します。この誘導性リアクタンスのことを「漏れリアクタンス」といいます。
励磁回路
変圧器の二次側を無負荷にして、一次側に電圧を加えたときに流れる電流を励磁電流 $\dot{I}_o$ いいます。励磁電流は、磁束を作る磁化電流と鉄損を発生させる鉄損電流からできています。この励磁回路を図2で表すと次のようになります。
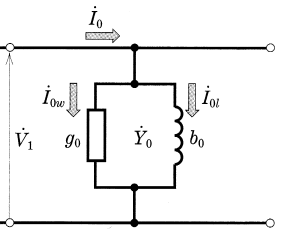
$\dot{I}_o$[A]:励磁電流
$g_o$[S]:励磁コンダクタンス
$b_o$[S]:励磁サセプタンス
$\dot{Y}_o$[S]:励磁アドミタンス
コンダクタンス $G$
抵抗 $R$ の逆数です。電流の流れやすさを表しています。単位は[S](読み:ジーメンス)を用います。
サセプタンス $B$
リアクタンス $X$ の逆数です。電流の流れやすさを表しています。単位は[S]を用います。
アドミタンス $Y$
インピーダンス $Z$ の逆数です。電流の流れやすさを表しています。単位は[S]を用います。アドミタンス $Y$ はコンダクタンス $G$ とサセプタンス $B$ を合わせたもので、式は $Y=G+jB$ と表します。アドミタンスの実数部がコンダクタンス $G$ で、虚数部がサセプタンス $B$ となります。
変圧器の等価回路
図2の励磁回路を、図1の理想変圧器の等価回路に組み込んだ回路を「変圧器の等価回路」(図3)といいます。
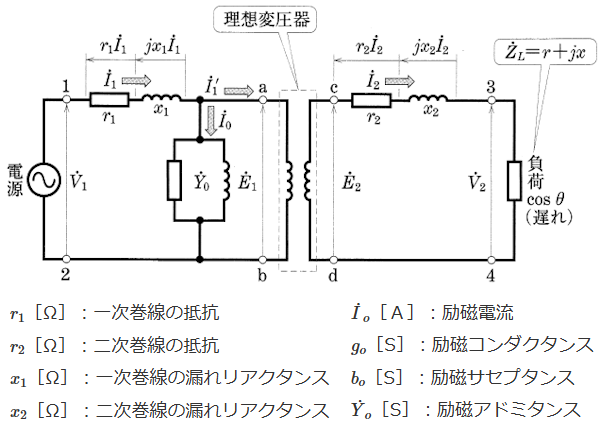
この等価回路において、$\dot{Z}_1=r_1+jx_1$[Ω]を一次インピーダンスといい、$(r_1+jx_1)\dot{I}_1$[V]を一次インピーダンス降下といいます。また、$\dot{Z}_2=r_2+jx_2$[Ω]を二次インピーダンスといい、$(r_2+jx_2)\dot{I}_2$[V]を二次インピーダンス降下といいます。この回路の電圧と電流の間には、次の関係があります。
$\dot{V}_1=\dot{E}_1+\dot{Z}_1\dot{I}_1$
$=\dot{E}_1+(r_1+jx_1)\dot{I}_1$
$=\dot{E}_1+r_1\dot{I}_1+jx_1\dot{I}_1$ … (1)
$\dot{E}_2=\dot{V}_2+\dot{Z}_2\dot{I}_2$
$=\dot{V}_2+(r_2+jx_2)\dot{I}_2$
$=\dot{V}_2+r_2\dot{I}_2+jx_2\dot{I}_2$ … (2)
$\dot{V}_2=\dot{Z}_L\dot{I}_2$ … (3)
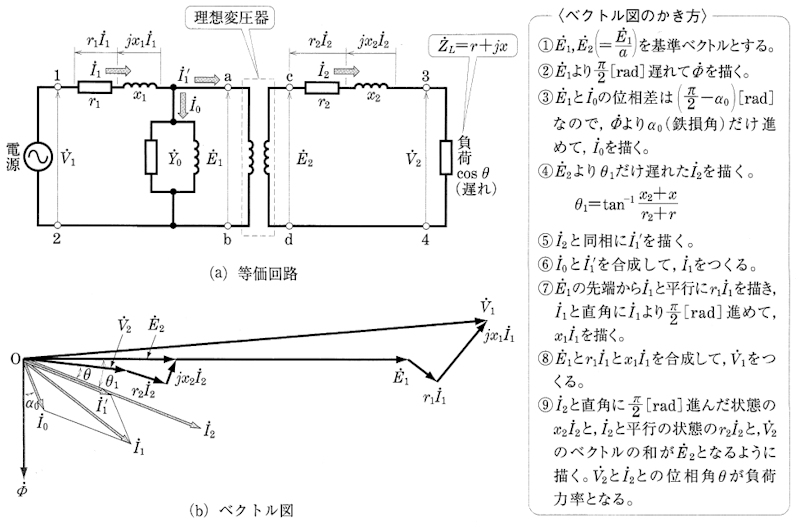
式(1),(2),(3)から電圧と電流のベクトル図を書くと、図4(b)のようになります。
理想変圧器を取り去った等価回路
図3の回路の電圧・電流およびインピーダンスなどを計算する場合、点線で囲まれた理想変圧器の部分を取り外し、単一電気回路として考えると便利です。この目的のために図5の回路に置き換え、電気的に等価になる条件を考えます。
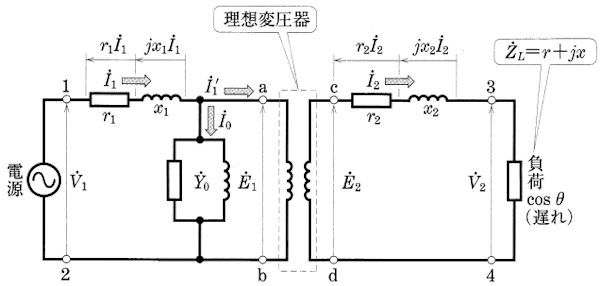
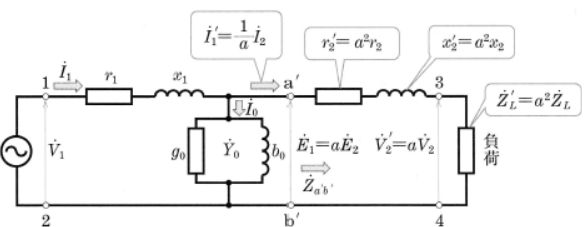
図3の端子a,bから右のほうのインピーダンスを $\dot{Z}_{ab}$[Ω]、端子c,dから右のほうのインピーダンスを $\dot{Z}_{cd}$[Ω]、図5のa’,b’から右のほうのインピーダンスを $\dot{Z}_{α′b′}$[Ω]とした場合、次の式がなりたちます。
$\dot{Z}_{ab}=\displaystyle\frac{\dot{E}_1}{\dot{I}_1′}=\displaystyle\frac{a\dot{E}_2}{\displaystyle\frac{1}{a} \dot{I}_2 }=a^2\displaystyle\frac{\dot{E}_2}{\dot{I}_2 }=a^2\dot{Z}_{cd}$
$\dot{Z}_{α′b′}=\displaystyle\frac{\dot{E}_1}{\dot{I}_1′}$
ここで、$\dot{Z}_{αb}=\dot{Z}_{α′b′}$ であれば、図3の回路と図5の回路は、等価になります。つまり、図5の二次側のインピーダンス $\dot{Z}_{α′b′}$ は一次側に換算すると、次のように表すことができます。
$\dot{Z}_{α′b′}=a^2\dot{Z}_{cd}$
図5の回路では、二次側の諸量を一次側に置き換え、一次回路はそのままと考えた回路で、一次側に換算した等価回路、または一次側からみた等価回路といいます。
二次側の諸量を一次側に換算する方法
- 電圧:$a$倍
- 電流:$\displaystyle\frac{1}{a}$倍
- インピーダンス:$a^2$倍
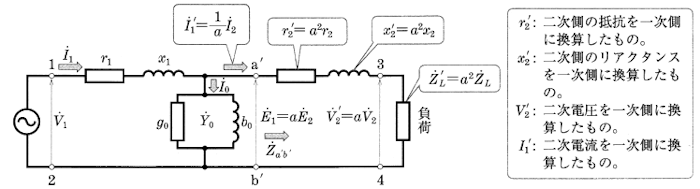
簡易等価回路
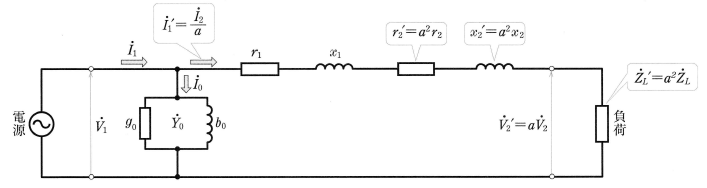
図5の回路では、$\dot{Y}_o$ の回路が一次インピーダンスと二次インピーダンスの中間に接続されていますので、回路計算が複雑になります。そこで、図6に示すように $\dot{Y}_o$ の回路を電源側に移すと回路計算が容易になります。
実際の変圧器では、一次インピーダンス降下は一次電圧 $V_1$[V]に比べて小さく、励磁電流 $I_o$[A]も一次電流 $I_1$[A]に比べて小さいので、図5と図6はほとんど等価とみることができます。図6の回路を簡易等価回路といい、図5のかわりによく用いられています。なお、 このような考えから、一次側の諸量をすべて二次側に置き換えた等価回路もつくることができます。

一次側の諸量を二次側に換算する方法
- 電圧: $\displaystyle\frac{1}{a}$倍
- 電流: $a$倍
- インピーダンス: $\displaystyle\frac{1}{a^2}$倍
電験三種-機械の過去問解説:変圧器の等価回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1997年(平成9年)問3
変圧器の一次側(巻数$N_1$)を二次側(巻数$N_2$)に換算した場合の簡易等価回路の換算係数に関する次の記述のうち、誤っているのは次のうちどれか。ただし、変圧器の巻数比($\displaystyle\frac{N_1}{N_2}$)は $a$ とする。
- 一次側の電圧は $\displaystyle\frac{1}{a}$倍
- 一次側の電流は $a$倍
- 励磁電流は $a$倍
- 一次側のインピーダンスは $(\displaystyle\frac{1}{a})^2$倍
- 励磁アドミタンスは $(\displaystyle\frac{1}{a})^2$倍
1997年(平成9年)問3 過去問解説
励磁アドミタンスはインピーダンスの逆数ですので、$a^2$倍になります。したがって、(5)が誤りです。
答え (5)
2014年(平成26年)問7
次の文章は、単相変圧器の簡易等価回路に関する記述である。
変圧器の電気的な特性を考える場合、等価回路を利用すると都合がよい。また、等価回路は負荷も含めた電気回路として考えると便利であり、特に二次側の諸量を一次側に置き換え、一次側の回路はそのままとした「一次側に換算した簡易等価回路」は広く利用されている。
一次巻線の巻数を $N_1$、二次巻線の巻数を $N_2$ とすると、巻数比 a は $a=N_1/N_2$ で表され、この $a$ を使用すると二次側諸量の一次側への換算は以下のように表される。
${\dot{V}_2}’$:二次電圧 ${\dot{V}_2}$ を一次側に換算したもの ${\dot{V}_2}’$=( ア )・${\dot{V}_2}$
${\dot{I}_2}’$:二次電流 ${\dot{I}_2}$ を一次側に換算したもの ${\dot{I}_2}’$=( イ )・${\dot{I}_2}$
${r_2}’$:二次抵抗 ${r_2}$ を一次側に換算したもの ${r_2}’$=( ウ )・${r_2}$
${x_2}’$:二次漏れリアクタンス ${x_2}$ を一次側に換算したもの ${x_2}’$=( エ )・${x_2}$
${\dot{Z}_L}’$:負荷インピーダンスを ${\dot{Z}_L}$ 一次側に換算したもの ${\dot{Z}_L}’$=( オ )・${\dot{Z}_L}$
ただし、’(ダッシュ)の付いた記号は、二次側諸量を一次側に換算したものとし、’(ダッシュ)のない記号は二次側諸量とする。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | $a$ | $\displaystyle\frac{1}{a}$ | $a^2$ | $a^2$ | $a^2$ |
| (2) | $\displaystyle\frac{1}{a}$ | $a$ | $a^2$ | $a^2$ | $a$ |
| (3) | $a$ | $\displaystyle\frac{1}{a}$ | $\displaystyle\frac{1}{a^2}$ | $\displaystyle\frac{1}{a^2}$ | $\displaystyle\frac{1}{a^2}$ |
| (4) | $\displaystyle\frac{1}{a}$ | $a$ | $\displaystyle\frac{1}{a^2}$ | $\displaystyle\frac{1}{a^2}$ | $a^2$ |
| (5) | $\displaystyle\frac{1}{a}$ | $a$ | $\displaystyle\frac{1}{a^2}$ | $\displaystyle\frac{1}{a^2}$ | $\displaystyle\frac{1}{a^2}$ |
2014年(平成26年)問7 過去問解説
一次側に換算した簡易等価回路を示します。

${\dot{V}_2}’$:二次電圧 ${\dot{V}_2}$ を一次側に換算したもの ${\dot{V}_2}’$=( $a$ )・${\dot{V}_2}$
${\dot{I}_2}’$:二次電流 ${\dot{I}_2}$ を一次側に換算したもの ${\dot{I}_2}’$=( $\displaystyle\frac{1}{a}$ )・${\dot{I}_2}$
${r_2}’$:二次抵抗 ${r_2}$ を一次側に換算したもの ${r_2}’$=( $a^2$ )・${r_2}$
${x_2}’$:二次漏れリアクタンス ${x_2}$ を一次側に換算したもの ${x_2}’$=( $a^2$ )・${x_2}$
${\dot{Z}_L}’$:負荷インピーダンスを ${\dot{Z}_L}$ 一次側に換算したもの ${\dot{Z}_L}’$=( $a^2$ )・${\dot{Z}_L}$
答え (1)






