第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「電動機の慣性モーメントとはずみ車効果」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「電動機の慣性モーメントとはずみ車効果」の過去問題も解説しています。
力学に関する量とその単位記号
| 量 | 記号 | 単位 | 他の表し方 |
|---|---|---|---|
| 長さ | $L$ | メートル[m] | 1m = 102cm |
| 面積 | $A,S$ | 平方メートル[m2] | |
| 質量 | $m$ | キログラム[kg] グラム[g] トン[t] | 1kg = 103g |
| 時間 | $t$ | 秒[s] 分[min] 時[h] | |
| 速度 | $v$ | メートル毎秒[m/s] メートル毎分[m/min] メートル毎時[m/h] | |
| 加速度 | $a$ | メートル毎秒毎秒[m/s2] | |
| 角度 | $θ,Φ$ | ラジアン[rad] 度[°] | |
| 周期 | $T$ | 秒[s] | |
| 周波数 振動数 | $f,v$ | ヘルツ[Hz] | 1Hz=1s-1 |
| 角速度 角周波数 | $ω$ | ラジアン毎秒[rad/s] | |
| 力 | $F$ | ニュートン[N] | 1N=1kg・m/s2 |
| 力のモーメント | $M$ | ニュートンメート ル[N・m] | 1N・m=1kg・m2/s2 |
| トルク | $T$ | ニュートンメート ル[N・m] | |
| 慣性モーメント | $I,J$ | キログラム平方メ ートル[kg・m2] | |
| 仕事 | $A,W$ | ジュール[J] | 1J = 1N・m |
| 仕事率 動力 | $P$ | ワット[W] | 1W・s=1J/s |
| エネルギー | $E,W$ | ワット秒[W・s] ワット時[W・h] | 1W・s=1J 1W・h=3600J |
運動方程式
運動の第一法則
「すべての物体は、なんらかの力の作用を受けないときには、静止状態を続けるか、または、一直線上の等速運動の状態を維持し続ける」という「慣性の法則」をニュートンの運動の第一法則といいます。
運動の第二法則
「力の作用を受ける物体に生ずる加速度は、加えられた力に比例し、比例定数となりそのときの加速度の方向は、力の方向と一致する」これを、ニュートンの運動の第二法則といいます。
物体の質量 $m$[kg]、加速度を $a$[m/s2]とすると、力 $F$[N]は次の式で表わすことができます。
$F=ma$
運動の第三法則
「物体間で相互に働く力、すべての作用とその反作用は、大きさが相等しく方向が反対である。」これを、ニュートンの運動の第三法則または、「作用反作用の法則」といいます。
エネルギー保存の法則
エネルギーには、位置エネルギー,運動エネルギー,熱エネルギー,電気エネルギーなど様々な形態があります。
エネルギーとは、仕事をする能力のことであり、これらのエネルギーは、互いに変換することが可能です。そして、変換前後のエネルギーの総和は等しくなります。 これを「エネルギー保存の法則」といいます。
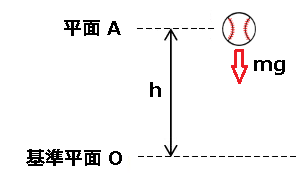
例えば、高さ $h$[m]の位置から $m$[kg]のボールを落下させた場合、平面Aの位置では、ボールに重力が加わっているため、重力によって仕事をすることができるエネルギーである「位置エネルギー」が存在します。位置エネルギーを $U$ とすると、
$U=mgh$
となります。
次に、基準平面Oまでボールを自由落下させた際、ボールが速度 $v$ で運動したとしましょう。このとき、最初に持っていた位置エネルギーが「運動エネルギー」に変換されることになり、運動エネルギー $W$ は、
$W=\displaystyle\frac{ 1 }{ 2 }mv^2$
となります。
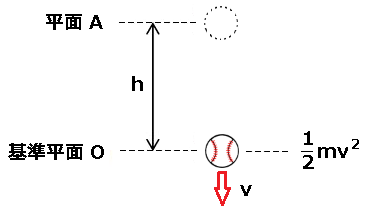
ボールが持っていた位置エネルギーは、落下するにつれて減少し、基準平面に達したときの位置エネルギーは完全にゼロとなり、反対に運動エネルギーは増加します。 これがエネルギー保存の法則です。
| 平面Aにおける エネルギーの総和 | 「運動エネルギー」+「位置エネルギー」$=0+mgh$ |
| 基準平面Oにおける エネルギーの総和 | 「運動エネルギー」+「位置エネルギー」$=\displaystyle \frac{ 1 }{ 2 }mv^2+0$ |
平面Aにおけるエネルギーの総和と基準平面Oにおけるエネルギーの総和は等しくなるため、
$mgh=\displaystyle \frac{ 1 }{ 2 }mv^2$
となります。
仕事と仕事率
物体に力 $F$[N]を加えて、力の方向に物体を $S$[m]だけ移動させたときの「仕事」 $W$[J]は、力 $F$[N]と移動距離 $S$[m]の積で表すことができます
$W=FS$[J]
1[N]の力で、1[m]だけ移動させた時、1[J]= 1[N・m] の仕事をしたことになります。
単位時間(1秒間)当たりにする仕事の割合を「仕事率」 $P$[W]といいます。仕事率は、動力 $P$[W]ともいいます。仕事を行なった間の時間を $t$[s]、速度を $v$[m/s]とすると仕事率 $P$[W]は、次の式で表わすことができます。
$P=\displaystyle\frac{W}{t}=Fv$[W]
1[s]当たりに 1[N・m]の仕事をする仕事率(動力)は、1[W]=1[N・m/s]となります。
回転運動
図のような、回転運動で t秒間に質点がOの回りを $θ$ だけ回転したとき、$θ$ を「角変位」といい、回転速度は $\displaystyle\frac{θ}{t}$ となります。この回転速度を、「角速度」 $ω$[rad/s]といいます。
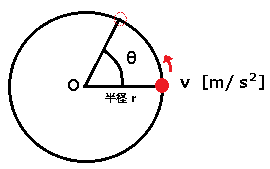
$ω=\displaystyle\frac{θ}{t}$[rad/s]
また、回転半径 $r$[m]の円周上を速さ $v$[m/s]で、物体が運動している場合、円周の長さは $2πr$ ですので、物体が円周を1周するのにかかる時間を $T$[s]とすると、
$v=\displaystyle\frac{2πr}{T}$
となります。物体が円周を1周するのにかかる時間を $T$[s]を、「周期」といいます。また、角速度 $ω$[rad/s]の定義より、
$ω=\displaystyle\frac{2π}{T}$[rad/s]
となります。円周上の速さ $v$[m/s]と角速度 $ω$[rad/s]の関係は、
$v=rω$[m/s]
という式が成り立ちます。同じ角速度なら、半径が大きいほど、大きな速さを持つことになります。
回転速度と角速度
回転速度 $N$[rpm または min-1]とは、1分間に回転する回数です。一方、角速度 $ω$[rad/s]は、回転の速さを表す単位です。一秒あたり何ラジアン角度が変化するかを表しています。
例えば、1[rpm]は、1分間に1回転することを示しています。つまり、1秒間では 1/60 回転します。また、1回転は $360$°$=2π$[rad]なので、1[rpm]は、1秒間に 2π/60[rad]回転すると考えることができます。したがって、次の式で表すことができます。
$ω=2π×\displaystyle\frac{N}{60}$[rad/s]
回転速度と角速度の関係式
$ω=2π×\displaystyle\frac{N}{60}$
$ω$[rad/s]:角速度
$N$[rpm または min-1]:回転速度
慣性モーメント
物体が持っている、運動を持続しようとする力を「慣性モーメント」といいます。ある速度で運動したとき、この速度を持続しようとする性質のことで、質量 m[kg]の物体が速度 $v$[m/s]で運動しているときの仕事(運動エネルギー)は、次の式で表すことができます。
$W=\displaystyle\frac{ 1 }{ 2 }mv^2$[J]
これを回転運動について考えると、$v=rω$[m/s]ですので、
$W=\displaystyle\frac{ 1 }{ 2 }mv^2=\displaystyle\frac{ 1 }{ 2 }m(rω)^2=\displaystyle\frac{ 1 }{ 2 }mr^2ω^2$[J]
$mr^2$ は回転数に関係ない定数で、この値を回転軸に対する慣性モーメントといいます。一般には、$J$ という記号で表されます。
$W=\displaystyle\frac{ 1 }{ 2 }Jω^2$[J]
回転体の運動エネルギーを求める式
$W=\displaystyle\frac{ 1 }{ 2 }Jω^2$
$W$[J]:運動エネルギー
$J$[kg・㎡]:慣性モーメント
$ω$[rad/s]:角速度
電動機の所要出力とはずみ車効果
電動機が力 $F$[N]、速度 $v$[m/s]である物体を引っ張っているとき、電動機の所要出力 $P$[W]は、次の式で表すことができます。
$P=Fv$[W]
電動機がトルク $T$[N・m]、角速度 $ω$[rad/s]で回転しているとき、電動機の所要出力 $P$[W]は、次の式で表すことができます。
$P=Tω$[W]
上記の二つの式より、$Tω=Fv$ となります。また、円周上の速さ $v$[m/s]と角速度 $ω$[rad/s]の関係は、$v=rω$[m/s]ですので、電動機のトルク $T$[N・m]と回転体の力 $F$[N]の関係は、次の式で表すことができます。
$T=rF$[N・m]
電動機の出力を求める式
$P=Tω$
$P$[W]:電動機の出力
$T$[N・m]:電動機のトルク
$ω$[rad/s]:角速度
電動機のトルクと回転力の関係式
$T=rF$
$T$[N・m]:電動機のトルク
$r$[m]:回転半径
$F$[N]:回転体の力
はずみ車効果
はずみ車とは、負荷のトルク変動が激しい場合に、電動機と負荷の間に取り付ける鉄製の重い車で、フライホイールともいいます。電動機で負荷とともに常時、はずみ車を回転させておくと、負荷トルクが急激に増加したとき、電動機の回転数は下がろうとしますが、このとき、はずみ車は慣性モーメントにより、等速運動を続けようとするので、負荷はこのエネルギー(トルク)をもらって回転し、電動機は定速運転ができます。このように、負荷トルクの変動に応じてはずみ車がエネルギーを放出したり、吸収することをはずみ車効果といいます。
はずみ車の全重量を G[kg]、直径を D[m]とすると、はずみ車効果は $GD^2$[kg⋅m2]で表すことができます。重量が重く、直径が大きいものほど効果は大きくなります。一般には、慣性モーメント $J$ の4倍、すなわち、$4J$[kg⋅m2]をはずみ車効果といいます。
はずみ車効果が大きい場合、電動機の始動あるいは制動時間が短いときは軸に大きなねじれ応力がかかり軸を破損します。また、慣性のため始動時間が長いときは電動機を加熱するので、電動機の選定にあたってはこれらを考慮する必要があります。
電験三種-機械の過去問解説:電動機の慣性モーメントとはずみ車効果
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1999年(平成11年)問6
慣性モーメント 30[kg・m2]のはずみ車の回転速度が、負荷の増加により 1000[r/min]から 800[r/min]に低下した場合、このはずみ車が放出したエネルギー[kJ]の値として、正しいのは次のうちどれか。
(1) 0.1π (2) 0.1π (3) 6π2 (4) 12π2 (5)22π2
1999年(平成11年)問6 過去問解説
慣性モーメントを $J$[kg⋅m2]、回転数を $N$[r/min]、角速度 $ω$[rad/s]、はずみ車が放出したエネルギーを $W$[kJ]とすると、
$ω=2π×\displaystyle\frac{N}{60}$[rad/s]
$W=\displaystyle\frac{ 1 }{ 2 }Jω^2$[J]
はずみ車の回転速度が、$ω_1$[rad/s]から $ω_2$[rad/s]に低下した場合に、放出したエネルギーを $W’$[kJ]は、
$W’=\displaystyle\frac{ 1 }{ 2 }J{ω_1}^2-\displaystyle\frac{ 1 }{ 2 }J{ω_2}^2$
$=\displaystyle\frac{ 1 }{ 2 }J({ω_1}^2-{ω_2}^2)$
$=\displaystyle\frac{ 1 }{ 2 }×30\left[\left(2π×\displaystyle\frac{1000}{60}\right)^2-\left(2π×\displaystyle\frac{800}{60}\right)^2\right]$
$=6π^2$[kJ]
答え (3)
2003年(平成15年)問17
慣性モーメント 100[kg・m2]のはずみ車が 1200[min-1]で回転している。このはずみ車について、次の(a)及び(b)に答よ。
(a) このはずみ車が持つ運動エネルギー[kJ]の値として、最も近いのは次のうちどれか。
(1) 6.28 (2) 20.2 (3) 395 (4) 790 (5) 1580
(b) このはずみ車に負荷が加わり、4秒間で回転速度が 1200[min-1]から 1000[min-1]まで減速した。この間にはずみ車が放出する平均出力[KW]の値として、最も近いのは次のうちどれか。
(1) 1.53 (2) 30.2 (3) 60.3 (4) 121 (5) 241
2003年(平成15年)問17 過去問解説
(a) 慣性モーメントを $J$[kg⋅m2]、回転数を $N$[r/min]、角速度 $ω$[rad/s]、はずみ車が持つ運動エネルギーを $W$[kJ]とすると、
$ω=2π×\displaystyle\frac{N}{60}$[rad/s]
$W=\displaystyle\frac{ 1 }{ 2 }Jω^2$
$=\displaystyle\frac{ 1 }{ 2 }J(2π×\displaystyle\frac{N}{60})^2$
$=\displaystyle\frac{ 1 }{ 2 }×100(2π×\displaystyle\frac{1200}{60})^2$
$=790$[kJ]
答え (4)
(b) $t=4$ 秒間で回転速度が $N_1=1200$[min-1]から $N_2=1000$[min-1]まで減速したはずみ車が放出する平均出力 $P$[KW]は、
$P=\displaystyle\frac{W_1-W_2}{t}$
$=\displaystyle\frac{\displaystyle\frac{ 1 }{ 2 }J{ω_1}^2-\displaystyle\frac{ 1 }{ 2 }J{ω_2}^2}{t}$
$=\displaystyle\frac{\displaystyle\frac{ J×(2π)^2 }{ 2 }×\left[(\displaystyle\frac{N_1}{60})^2-(\displaystyle\frac{N_2}{60})^2\right]}{t}$
$=\displaystyle\frac{\displaystyle\frac{ 100×(2π)^2 }{ 2 }×\left[(\displaystyle\frac{1200}{60})^2-(\displaystyle\frac{1000}{60})^2\right]}{4}$
$=60300=60.3$[kW]
答え (3)
2008年(平成20年)問11
図に示すように、電動機が減速機と組み合わされて負荷を駆動している。このときの電動機の回転速度が nm が 1150[min-1]、トルク Tm が 100[N・m]であった。減速機の減速比が 8、効率が 0.95 のとき、負荷の回転速度 nL[min-1]、軸トルク TL[N・m]及び軸入力 PL[kW]の値として、最も近いものを組み合わせたのは次のうちどれか。
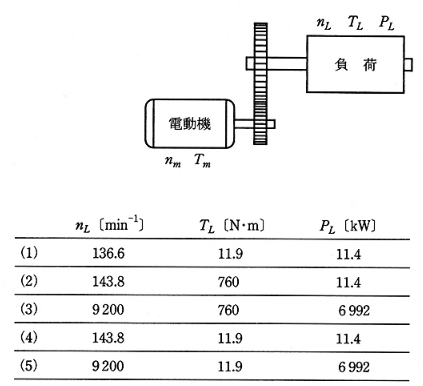
2008年(平成20年)問11 過去問解説
題意より、負荷の回転速度 $n_L$[min-1]は、電動機の回転速度が $n_m=1150$[min-1]の、$\displaystyle\frac{1}{8}$ 倍になりますので、
$n_L=\displaystyle\frac{1150}{8}≒143.8$[min-1]
負荷の軸トルク $T_L$[N・m]は、電動機のトルク $T_m=100$[N・m]に、減速機の減速比 8 と効率 0.95 を掛けた値になりますので、
$T_L=100×8×0.95=760$[N・m]
負荷の軸入力 $P_L$[kW]は、
$P_L=ω_LT_L=2π×\displaystyle\frac{n_L}{60}×T_L$
$=2π×\displaystyle\frac{143.8}{60}×760≒11400=11.4$[kW]
答え (2)
2013年(平成25年)問10
電動機ではずみ車を加速して、運動エネルギーを蓄えることを考える。
まず、加速するための電動機のトルクを考える。加速途中の電動機の回転速度を N[min-1]とすると、そのときの毎秒の回転速度 n[s-1]は①式で表される。
( ア ) ・・・①
この回転速度 n[s-1]から②式で角速度 ω[rad/s]を求めることができる。
( イ ) ・・・②
このときの電動機が1秒間にする仕事、すなわち出力を P[W]とすると、トルク T[N・m]は③式となる。
( ウ ) ・・・③
③式のトルクによってはずみ車を加速する。電動機が出力し続けて加速している間、この分のエネルギーがはずみ車に注入される。電動機に直結するはずみ車の慣性モーメントを I[kg・m2]として、加速が完了したときの電動機の角速度を ω0[rad/s]とすると、このはずみ車に蓄えられている運動エネルギー E[J]は④式となる。
( エ ) ・・・④
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

2013年(平成25年)問10 過去問解説
電動機ではずみ車を加速して、運動エネルギーを蓄えることを考える。
まず、加速するための電動機のトルクを考える。加速途中の電動機の回転速度を N[min-1]とすると、そのときの毎秒の回転速度 n[s-1]は①式で表される。
( $n=\displaystyle\frac{N}{60}$ ) ・・・①
この回転速度 n[s-1]から②式で角速度 ω[rad/s]を求めることができる。
( $ω=2π×n$ ) ・・・②
このときの電動機が1秒間にする仕事、すなわち出力を P[W]とすると、トルク T[N・m]は③式となる。
( $T=\displaystyle\frac{P}{ω}$ ) ・・・③
③式のトルクによってはずみ車を加速する。電動機が出力し続けて加速している間、この分のエネルギーがはずみ車に注入される。電動機に直結するはずみ車の慣性モーメントを I[kg・m2]として、加速が完了したときの電動機の角速度を ω0[rad/s]とすると、このはずみ車に蓄えられている運動エネルギー E[J]は④式となる。
( $E=\displaystyle\frac{1}{2}I{ω_0}^2$ ) ・・・④
答え (5)






