第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、配電理論及び配線設計「配電方式」について、解説しています。
低圧配電の種類
低圧配電線を通して、一般家庭などに電気を供給するとき、その方式として主に「単相2線式」「単相3線式」「三相3線式」の3種類があります。
単相2線式配電方式
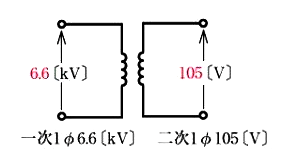
主に小規模の低圧配電に使用されます。往復2線で単相電圧 100 や 200[V]を供給する方式で、電灯および小形動力回路に採用されます。
この方式では1種類の電圧しか得られないことと、100[V]系では電圧降下、線路損失が大きくなるので、小規模の電灯、コンセント回路のほかには用いられません。
単相3線式配電方式
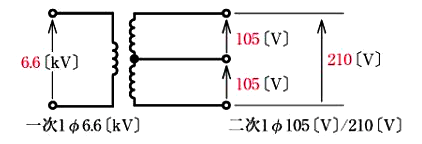
二次低圧側の中性点を接地(B種接地工事)して、両外線および中性線の3線を引き出し、外線~中性線間で単相100[V]、両外線間で単相200[V]を供給する電気方式です。
この方式では、2種類の電圧が得られることと、単相100[V]負荷が平衡していれば、中性線電流は相殺して零となり、単相2線式に比べ、電圧降下、線路損失の面で有利となります。反面、二次側配線のこう長が長いか、線が細くて電気抵抗が比較的大きい場合には、負荷が不平衡であれば、負荷電圧が不平衡になる欠点があります。
この方式で中性線が断線すれば、負荷電圧が極端に不平衡になり機器を損傷するおそれがあるため、「多線式電路の中性線には過電流遮断器を施設してはならない」としています。
三相3線式配電方式
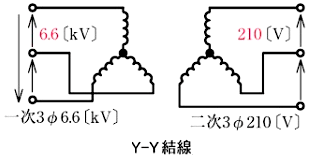
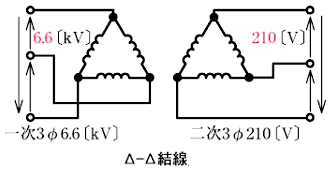
3線に対称三相交流電圧をかけて送電する電気方式です。低圧配電では比較的容量の大きい動力負荷にはこの方式で給電することが多いです。
平衡三相交流の瞬時電力は、電圧、電流、力率が一定であれば、原理的に、時間的に一定(すなわち脈動がない)であり、回転機(発電機、電動機など)にとって都合がよいことが、この方式が多く採用される理由です。
配電理論及び配線設計:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 単相3線式回路①
図のような単相3線式回路において、消費電力 250[W]、1000[W]の2つの負荷はともに抵抗負荷である。図中の×印点で断線した場合、b-c 間の電圧[V]は。
ただし、断線によって負荷の抵抗値は変化しないものとする。
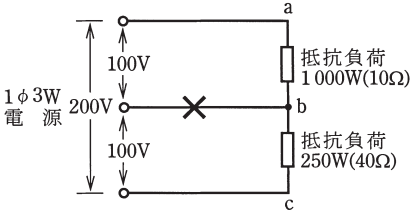
イ. 80 ロ. 100 ハ. 160 二. 200
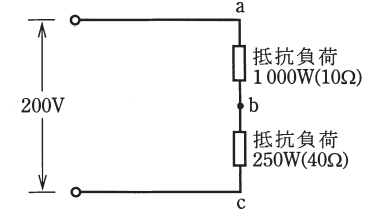
断線後は単相 200V の回路になります。回路の合成抵抗を $R$[Ω]、流れる電流を $I$[A]とすると、
$R=40+10=50$[Ω]
$I=\displaystyle\frac{V}{R}=\displaystyle\frac{200}{50}=4$[A]
b-c 間の電圧 $V_{bc}$[V]は、
$V_{bc}=R_{bc}I=40×4=160$[V]
答え(ハ)
2006年(平成18年)問6
2009年(平成21年)問7
2012年(平成24年)下期 問8 類似
2014年(平成26年)下期 問8 類似
2016年(平成28年)上期 問7 類似
2019年(令和元年)下期 問6 類似
問2 単相3線式回路②
図のような単相3線式回路で電流計(A)の指示値が最も小さいものは。
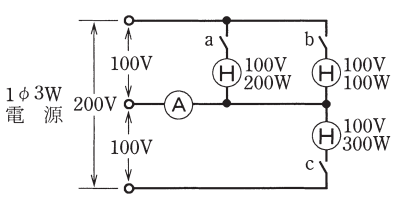
- スイッチa,bを閉じた場合。
- スイッチa,cを閉じた場合。
- スイッチb,cを閉じた場合。
- スイッチa,b,cを閉じた場合。
単相3線式回路は、単相100[V]負荷が平衡していれば、中性線電流は相殺して零となります。スイッチa,b,cを閉じた場合、上側の並列回路の負荷を合計すると、100W+200W=300W となり、下側の負荷 300W と平衡しますので、中性線に流れる電流は 0[A]になります。
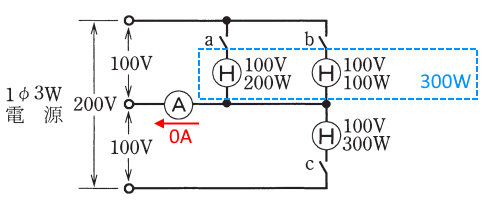
答え(二)
2010年(平成22年)問6
問3 単相3線式回路③
図のような単相 3 線式回路で電流計(A)の指示値が最も小さいものは。ただし、(H) は定格電圧 100[V]の電熱器である。
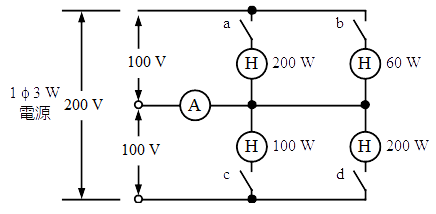
- スイッチa,bを閉じた場合。
- スイッチc,dを閉じた場合。
- スイッチa,dを閉じた場合。
- スイッチa,b,dを閉じた場合。
単相3線式回路は、単相100[V]負荷が平衡していれば、中性線電流は相殺して零となります。スイッチa,dを閉じた場合、上側の負荷 200W と、下側の負荷 200W が平衡しますので、中性線に流れる電流は 0[A]になります。
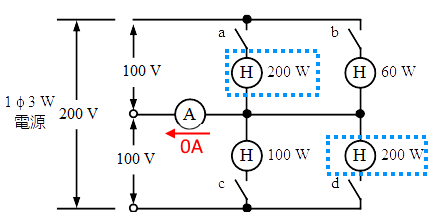
答え(ハ)
2013年(平成25年)上期 問7
問4 単相3線式回路④
図のような単相3線式回路で、消費電力 1[W],2[W],3[W]の負荷はすべて抵抗負荷である。電流計の指示値[A]は。
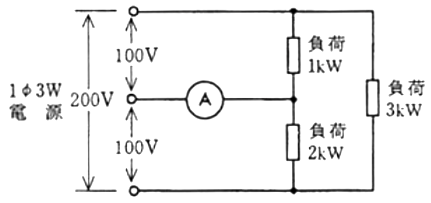
イ. 0 ロ. 10 ハ. 20 二. 40
単相3線式の中性線に流れる電流は、a の負荷に流れる電流と b の負荷に流れる電流の差分が流れます。a と b に流れる電流の大きい値から小さい値を引きます。尚、200V 回路の 3kw の負荷に流れる電流は中性線とは無関係です。
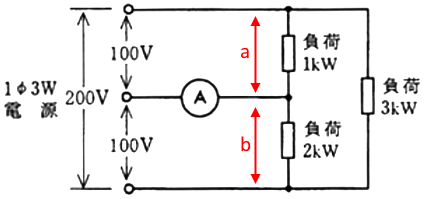
a の負荷に流れる電流は、
$I_a=\displaystyle\frac{P_a}{V_a}=\displaystyle\frac{1000}{100}=10$[A]
b の負荷に流れる電流は、
$I_b=\displaystyle\frac{P_b}{V_b}=\displaystyle\frac{2000}{100}=20$[A]
したがって、中性線に流れる電流は、
$20-10=10$[A]
答え(ロ)
2006年(平成18年)問4
問5 単相3線式回路⑤
図のような単相3線式回路で、開閉器を閉じて機器Aの両端の電圧を測定したところ150[V]を示した。この原因として、考えられるものは。
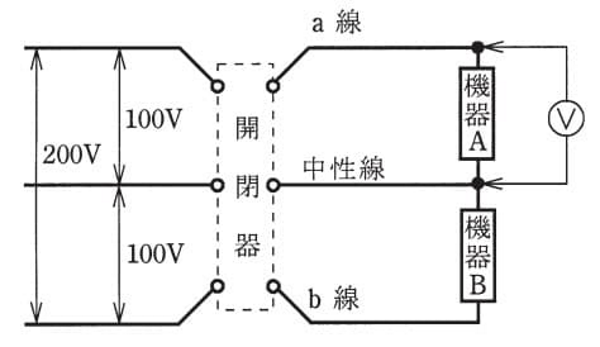
- 機器Aの内部で断線している。
- a線が断線している。
- 中性線が断線している。
- b線が断線している。
中性線が断線した場合、回路は機器AとBの直列接続となり、A,B機器の抵抗値によって電圧は変わります。従って、中性線が断線している(ハ)が正解となります。
答え(ハ)
2014年(平成26年)上期 問24
2018年(平成30年)下期 問27
2019年(令和元年)上期 問24
問6 三相3線式回路①
図のような電源電圧 $E$[V]の三相 3 線式回路で、図中の × 印点で断線した場合、断線後の a-c 間の抵抗 $R$[Ω]に流れる電流 $I$[A]を示す式は。
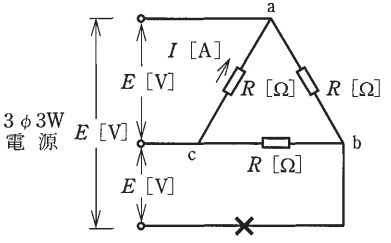
イ. $\displaystyle\frac{E}{2R}$ ロ. $\displaystyle\frac{E}{\sqrt{3}R}$ ハ. $\displaystyle\frac{E}{R}$ 二. $\displaystyle\frac{3E}{2R}$
断線後の回路図を示します。
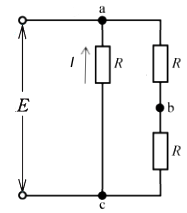
$I$ は、オームの法則より、
$I=\displaystyle\frac{E}{R}$
答え(ハ)
2015年(平成27年)上期 問5
問7 三相3線式回路②
図のような電源電圧 $E$[V]の三相 3 線式回路で、× 印点で断線すると、断線後の a-b 間の抵抗 $R$[Ω]に流れる電流 $I$[A]は。
イ. $\displaystyle\frac{E}{2R}$ ロ. $\displaystyle\frac{E}{\sqrt{3}R}$ ハ. $\displaystyle\frac{E}{R}$ 二. $\displaystyle\frac{3E}{2R}$
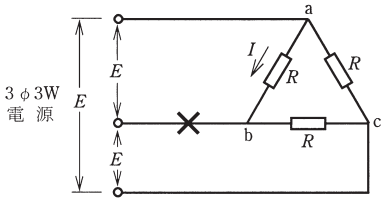
各線路に流れる電流を図のように決めた断線後の回路図を示します。
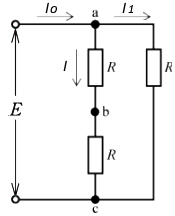
$I_1$ は、オームの法則より、
$I_1=\displaystyle\frac{E}{R}$
合成抵抗を $R_o$、電源より流れる電流を $I_o$ とすると、
$R_o=\displaystyle\frac{2R×R}{2R+R}=\displaystyle\frac{2R}{3}$
$I_o=\displaystyle\frac{E}{\displaystyle\frac{2R}{3}}=\displaystyle\frac{3E}{2R}$
a 点の電流の分流に注目すると、$I_o=I_1+I$ となっていますので、
$I=I_o-I_1=\displaystyle\frac{3E}{2R}-\displaystyle\frac{E}{R}=\displaystyle\frac{E}{2R}$
答え(イ)
2011年(平成23年)上期 問5
問8 三相3線式回路③
図のような三相3線式200[V]の回路で、c – o 間の抵抗が断線した。断線前と断線後の a – o 間の電圧 $V$ の値[V]の組合せとして正しいものは。
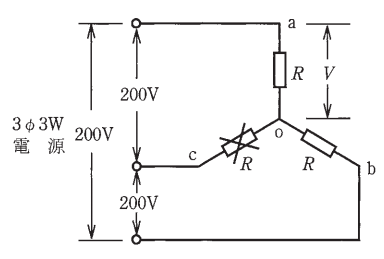
- 断線前 116,断線後 100
- 断線前 116,断線後 116
- 断線前 100,断線後 116
- 断線前 100,断線後 100
断線前の a – o 間の電圧 $V$ [V]は、スター結線の相電圧ですので、
$V=\displaystyle\frac{E}{\sqrt{3}}=\displaystyle\frac{200}{\sqrt{3}}≒116$ [V]
断線後の a – o 間の電圧 $V$ [V]は、単相 200V の電圧を 2個の抵抗 $R$ で分担した電圧となりますので、抵抗 $R$ 一個分の電圧は、100V になります。
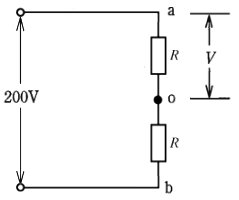
答え(イ)
2007年(平成19年)問5
2013年(平成25年)上期 問5
2017年(平成29年)上期 問5



