第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、電気に関する基礎理論「単相交流回路」について、解説しています。
交流とは?
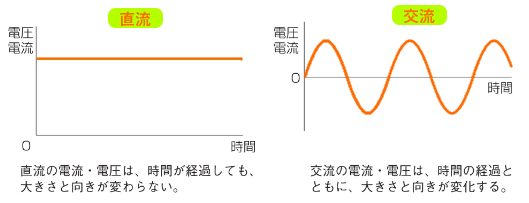
電気には直流と交流があります。直流は乾電池などが作る大きさと流れの向きが変化しない電気です。交流は発電所などで作られて送られてくる大きさと流れの向きが変わる電気です。電流と電圧の大きさと時間のグラフを作ると、次のような形になります。
交流の値を表す量
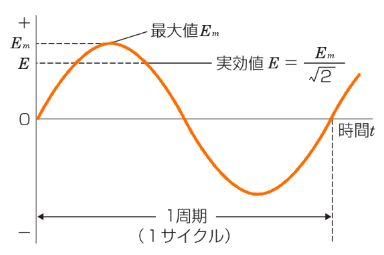
交流の値を表す量として、瞬時値,最大値,実効値が用いられます。
- 瞬時値・・・変化する交流の瞬間、瞬間の値。
- 最大値・・・瞬時値が最も大きくなる値。
- 実効値・・・直流回路で発生する電力と同じ電力を発生させる交流回路の電流と電圧。交流の値として、通常用いられています。
交流を波形で表すと、同じ波形を繰り返します。この1回の繰返しに要する時間を周期 $T$[s]といい、1秒間に繰り返す回数を周波数 $f$[Hz]といいます。
最大値と実効値の関係
$実効値=\displaystyle\frac{最大値}{\sqrt{2}}$
周期と周波数の関係
$T=\displaystyle\frac{1}{f}$
交流回路の負荷の働き
交流回路に、抵抗,コイル,コンデンサの負荷を接続したときの電圧と電流の関係を説明します。
交流電源に抵抗を接続した回路
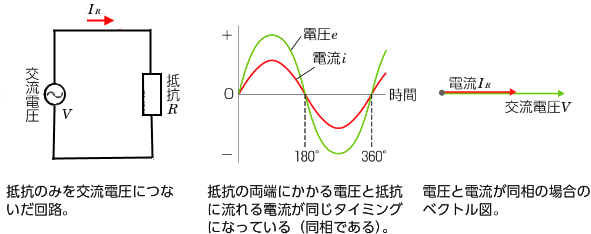
直流回路と同じように、抵抗は電流を妨げる働きをします。また、抵抗に流れる電流を熱エネルギーに変えてエネルギーを消費します。
交流の電圧や電流は、縦軸に電圧や電流の大きさ、横軸に時間をとったグラフです。抵抗を接続した交流回路では、電圧が最大のときは電流も最大に、電圧が最小のときは電流も最小になるように、プラスとマイナスのタイミングが一致します。このことを、「位相が合う」や「同相である」といいます。
このように抵抗のみの負荷の場合は、電圧と電流に位相のずれがありませんので、どのタイミングでも、オームの法則が成り立ちます。
尚、位相のずれがある場合は、大きさとその方向も考えなければなりませんので、ベクトルで考えなければなりません。
交流電源に抵抗を接続した回路
交流電源にコイルを接続した回路
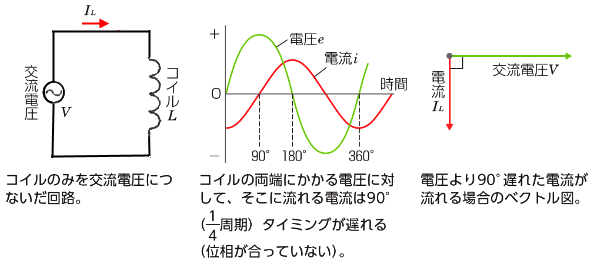
コイル(記号:L)は、導線をぐるぐると巻き付けたものです。直流では普通の導線と変わりませんが、交流では、変化する電流に対してその流れを妨げる働きがあります。この性質をインダクタンスといい、単位はヘンリー(記号:H)です。
コイルに加わる電圧とその周波数、コイルに流れる電流との間には次の関係があります。
コイルに流れる交流電流とインダクタンスの関係
$I=\displaystyle\frac{V}{2πfL}$[A]
$I$:電流[A]
$V$:電圧[V]
$f$:電圧の周波数[Hz]
$L$:インダクタンス[H]
電圧と電流に注目すると、$2πfL$ はオームの法則の抵抗と同様の働きをしていることが分かります。そこで、$2πfL$ を交流に対する負荷ととらえ、誘導性リアクタンス $X_L$ と定義されています。単位はオーム[Ω]です。
誘導性リアクタンス
$X_L=2πfL$[Ω]
コイルに流れる交流電流とインダクタンスの関係を誘導性リアクタンスを使って表すと、
$I=\displaystyle\frac{V}{X_L}$[Ω]
コイルは、電流の変化を妨げる性質がありますので、その変化を打ち消す方向に電圧を発生させます。これは、コイルに流れる電流は、コイルにかかる電圧より90°(\displaystyle\frac{1}{4}周期)位相が遅れることを引き起こします。
交流電源にコイルを接続した回路
交流電源にコンデンサを接続した回路
コンデンサ(記号:C)は、2枚の電極板を向い合わせにしたものです。直流では普通の充電池のような働きがありますが、交流では、変化する電流に対してその流れを助長する働きがあります。この性質をキャパシタンスといい、単位はファラド(記号:F)です。
コンデンサに加わる電圧とその周波数、コンデンサに流れる電流との間には次の関係があります。
コンデンサに流れる交流電流とキャパシタンスの関係
$I=2πfCV$[A]
$I$:電流[A]
$V$:電圧[V]
$f$:電圧の周波数[Hz]
$C$:キャパシタンス[F]
電圧と電流に注目すると、$\displaystyle\frac{1}{2πfC}$ はオームの法則の抵抗と同様の働きをしていることが分かります。そこで、$\displaystyle\frac{1}{2πfC}$ を交流に対する負荷ととらえ、容量性リアクタンス $X_C$ と定義されています。単位はオーム[Ω]です。
容量性リアクタンス
$X_C=\displaystyle\frac{1}{2πfC}$[Ω]
コンデンサに流れる交流電流とキャパシタンスの関係を容量性リアクタンスを使って表すと、
$I=\displaystyle\frac{V}{X_C}$[Ω]
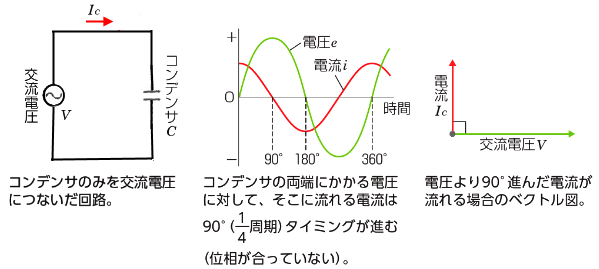
コンデンサは、電流の変化を助長する性質がありますので、その変化を助ける方向に電圧を発生させます。これは、コンデンサに流れる電流は、コンデンサにかかる電圧より90°(\displaystyle\frac{1}{4}周期)位相が進むことを引き起こします。
交流電源にコンデンサを接続した回路
交流回路の合成インピーダンス
$R,L,C$ が混在した回路では、各負荷で電圧と電流の位相差が異なりますので、計算が困難です。その解決策としてベクトル図を用いると計算が簡単にできます。ベクトルとは「大きさ」と「方向」を持った記号で、電圧と電流の各ベクトルの相対的な方向を覚えておいてください。
RLC直列回路
RLC直列回路では、各負荷に共通の電流 $i$[A]が流れ、各負荷ごとに電圧の大きさと位相が異なります。そのため、電流を基準としたベクトル図を作成します。
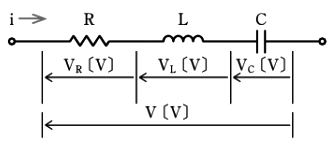
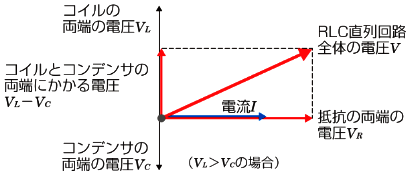
各負荷の電圧ベクトルを合成すると、RLC直列回路の両端から見た電圧 $V$[V]になります。三平方の定理より、
$V^2={V_R}^2+({V_L}-{V_C})^2$
ですので、$V$[V]が求まります。
RLC直列回路全体の電圧 V
$V=\sqrt{{V_R}^2+({V_L}-{V_C})^2}$
さらに、各負荷の電圧ベクトルの大きさを電流 $I$[A]で割ると、各負荷のインピーダンスの大きさが求まります。
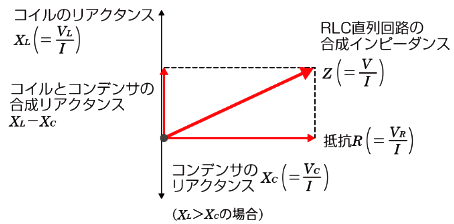
各インピーダンスのベクトルを合成することで、RLC直列回路の両端から見た合成インピーダンス $Z$[Ω] になります。三平方の定理より、
$Z^2={R}^2+({X_L}-{X_C})^2$
ですので、$Z$[Ω]が求まります。
RLC直列回路の合成インピーダンス Z
$Z=\sqrt{{R}^2+({X_L}-{X_C})^2}$
RLC並列回路
RLC並列回路では、各負荷に共通の電圧 $v$[V]が加わり、各負荷ごとに電流の大きさと位相が異なります。そのため、電圧を基準としたベクトル図を作成します。
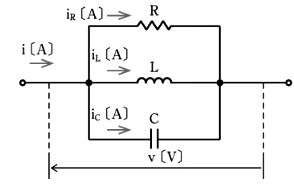
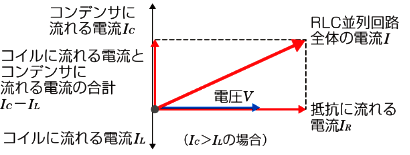
各負荷の電流ベクトルを合成すると、RLC並列回路の両端から見た電流 $I$[A]になります。三平方の定理より、
$I^2={I_R}^2+({I_C}-{I_L})^2$
ですので、$I$[A]が求まります。
RLC並列回路全体の電圧 I
$I=\sqrt{{I_R}^2+({I_C}-{I_L})^2}$
さらに、各負荷の電流ベクトルの大きさを電圧 $V$[V]で割ると、各負荷のインピーダンスの大きさの逆数が求まります。
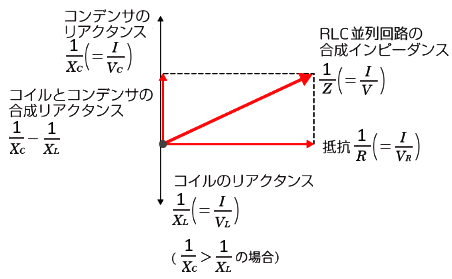
各インピーダンスのベクトルを合成することで、RLC並列回路の両端から見た合成インピーダンス $Z$[Ω] の逆数になります。三平方の定理より、
$\left(\displaystyle\frac{1}{Z}\right)^2=\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)^2$
ですので、$Z$[Ω]が求まります。
RLC並列回路の合成インピーダンス Z
$Z=\displaystyle\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)^2}}$
交流の電力と力率
交流回路では、電力 $P$[W]を、次の式で表すことができます。
$P=VIcosθ$[W]
$V$[V]: 電圧の実効値
$I$[A]:電流の実効値
$cosθ$:電圧と電流の位相差
尚、$cosθ$ のことを力率といいます。力率は負荷のインピーダンス $Z$[Ω]に対する、抵抗 $R$[Ω]の比で表すことができます。
$cosθ=\displaystyle \frac{R}{Z}$
交流電力のベクトル表示
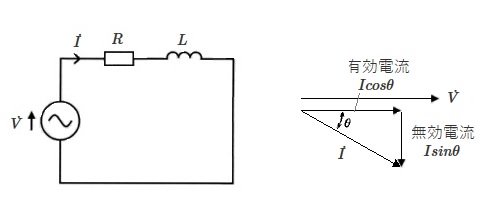
図のような $RL$ 直列回路では、電圧 $\dot{V}$[V]を加えると、電流 $\dot{I}$[A]が流れます。電流 $\dot{I}$ は、電圧 $\dot{V}$ より $θ$ 遅れます。
電流 $\dot{I}$ は、電圧 $\dot{V}$ と同相の $Icosθ$ の有効電流と電圧 $\dot{V}$ より $90°$遅れた $Isinθ$ の無効電流に分けることができます。この有効電流と無効電流に電圧 $V$ を掛けた値は、それぞれ電力を表します。
交流電力には、皮相電力 $S$[V・A]、有効電力 $P$[W]、無効電力 $Q$[var]があり、次のように表すことができます。
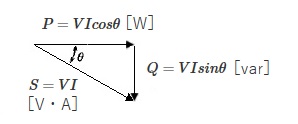
皮相電力:$S=VI=I^2Z$[V・A]
有効電力:$P=VIcosθ=I^2R$[W]
無効電力:$Q=VIsinθ=I^2X_L$[var]
上記3式の関係は次のように表すことができます。
$S=\sqrt{P^2+Q^2}$
電気に関する基礎理論:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 最大値と実効値①
実効値が 105[V]の正弦波交流電圧の最大値[V]は。
イ. 105 ロ. 148 ハ. 182 二. 210
実効値 $V$[V]の正弦波交流電圧の最大値を $V_m$[V]とすると、
$V_m=\sqrt{2}V=1.41×105≒148$[V]
答え(ハ)
2010年(平成22年)問2
問2 最大値と実効値②
実効値が 210[V]の正弦波交流電圧の最大値[V]は。
イ. 210 ロ. 296 ハ. 363 二. 420
実効値 $V$[V]の正弦波交流電圧の最大値を $V_m$[V]とすると、
$V_m=\sqrt{2}V=1.41×210≒296$[V]
答え(ロ)
2007年(平成19年)問1
問3 最大値と実効値③
最大値が 148[V]の正弦波交流電圧の実効値[V]は。
イ. 85 ロ. 105 ハ. 148 二. 209
最大値 $V_m$[V]の正弦波交流電圧の実効値を $V$[V]とすると、
$V=\displaystyle\frac{V_m}{\sqrt{2}}=\displaystyle\frac{148}{1.41}≒105$[V]
答え(ロ)
2014年(平成26年)上期 問1
問4 コイルに流れる電流
コイルに 100[V]、50[Hz]の交流電圧を加えたら 6[A]の電流が流れた。このコイルに100[V]、60[Hz]の交流電圧を加えたときに流れる電流[A]は。
ただし、コイルの抵抗は無視できるものとする。
イ. 2 ロ. 3 ハ. 4 二. 5
コイルに 100[V]、50[Hz]の交流電圧を加えたら 6[A]の電流が流れたますので、コイルに流れる交流電流とインダクタンスの関係より、
$I=\displaystyle\frac{V}{2πfL}$
$L=\displaystyle\frac{V}{2πfI}=\displaystyle\frac{100}{2π×50×6}=\displaystyle\frac{1}{6π}$
100[V]、60[Hz]の交流電圧を加えたときに流れる電流[A]は、
$I=\displaystyle\frac{V}{2πfL}=\displaystyle\frac{100}{2π×60×\displaystyle\frac{1}{6π}}=5$[A]
答え(二)
2009年(平成21年)問2
2013年(平成25年)下期 問2
2015年(平成27年)下期 問2
2018年(平成30年)上期 問2
問5 交流回路の波形①
図のように正弦波交流回路の電源電圧 $v$ に対する電流 $i$ の波形として、正しいものは。
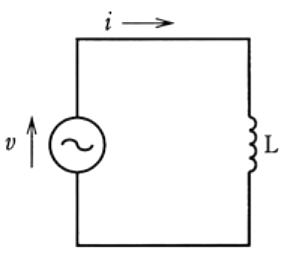
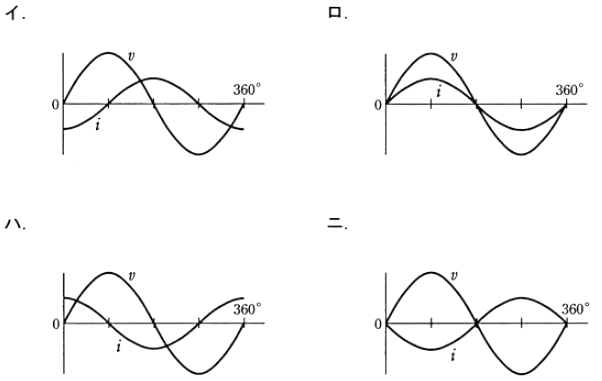
コイル $L$ だけの回路では、電圧 $v$ に対して電流 $i$ の波形は90°遅れます。
- 電源電圧 $v$ に対して、電流 $i$ は 90°遅れ
- 電源電圧 $v$ に対して、電流 $i$ の位相差は0°
- 電源電圧 $v$ に対して、電流 $i$ は 90°進み
- 電源電圧 $v$ に対して、電流 $i$ は逆位相(180°のずれ)
答え(イ)
2008年(平成20年)問1
問6 交流回路の波形②
図のように正弦波交流回路の電源電圧 $v$ に対する電流 $i$ の波形として、正しいものは。
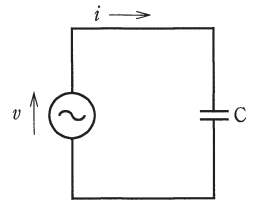

コンデンサ $C$ だけの回路では、電圧 $v$ に対して電流 $i$ の波形は90°進みます。
- 電源電圧 $v$ に対して、電流 $i$ は 90°遅れ
- 電源電圧 $v$ に対して、電流 $i$ の位相差は0°
- 電源電圧 $v$ に対して、電流 $i$ は 90°進み
- 電源電圧 $v$ に対して、電流 $i$ は逆位相(180°のずれ)
答え(ハ)
2019年(令和元年)下期 問4
問7 交流回路のインピーダンス①
図のような交流回路において、抵抗 12 Ω の両端の電圧 $V$[V]は。
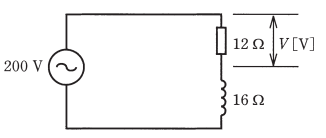
イ. 86 ロ. 114 ハ. 120 二. 160
回路の合成インピーダンスを $Z$[Ω]とすると、
$Z=\sqrt{{R}^2+{X_L}^2}=\sqrt{12^2+16^2}=20$[Ω]
回路に流れる電流を $I$[A]とすると、
$I=\displaystyle\frac{電源電圧}{Z}=\displaystyle\frac{200}{20}=10$[A]
抵抗 12 Ω の両端の電圧 $V$[V]は
$V=RI=12×10=120$[V]
答え(ハ)
2012年(平成24年)下期 問2 類似
2016年(平成28年)上期 問2
2017年(平成29年)下期 問2 類似
2018年(平成30年)下期 問2
2019年(令和元年)上期 問4 類似
問8 交流回路のインピーダンス②
図のような交流回路で、リアクタンス 8[Ω]の両端の電圧 $V$[V]は。
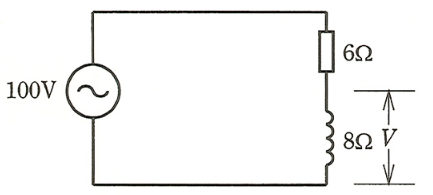
イ. 43 ロ. 57 ハ. 60 二. 80
回路の合成インピーダンスを $Z$[Ω]とすると、
$Z=\sqrt{{R}^2+{X_L}^2}=\sqrt{6^2+8^2}=10$[Ω]
回路に流れる電流を $I$[A]とすると、
$I=\displaystyle\frac{電源電圧}{Z}=\displaystyle\frac{100}{10}=10$[A]
リアクタンス 8[Ω]の両端の電圧 $V$[V]は
$V=X_LI=8×10=80$[V]
答え(二)
2011年(平成23年)下期 問2
問9 交流の電力と力率①
単相 200[V]の回路に、消費電力 2.0[kW]、力率 80[%]の負荷を接続した場合、回路に流れる電流[A]は。
イ. 5.8 ロ. 8.0 ハ. 10.0 二. 12.5
電圧を $V$[V]、電流を $I$[A]、力率 $cosθ$ の交流回路の消費電力 $P$[W]は、
$P=VIcosθ$[W]
$I=\displaystyle\frac{P}{Vcosθ}=\displaystyle\frac{2000}{200×0.8}=12.5$[A]
答え(二)
2011年(平成23年)下期 問3
2012年(平成24年)下期 問4
2014年(平成26年)下期 問5
問10 交流の電力と力率②
図のような交流回路の力率[%]を示す式は。
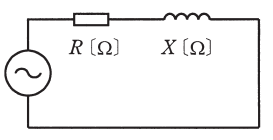
イ. $\displaystyle\frac{100R}{\sqrt{R^2+X^2}}$ ロ. $\displaystyle\frac{100RX}{R^2+X^2}$ ハ. $\displaystyle\frac{100R}{R+X}$ 二. $\displaystyle\frac{100X}{\sqrt{R^2+X^2}}$
回路の合成インピーダンスを $Z$[Ω]とすると、
$Z=\sqrt{{R}^2+{X}^2}$
力率 $cosθ$[%]は、
$cosθ=\displaystyle\frac{R}{Z}×100=\displaystyle\frac{100R}{\sqrt{{R}^2+{X}^2}}$[%]
答え(イ)
2011年(平成23年)上期 問4
問11 交流の電力と力率③
図のような交流回路で、抵抗の両端の電圧が 80[V]、リアクタンスの両端の電圧が 60[V]であるとき、負荷の力率[%]は。
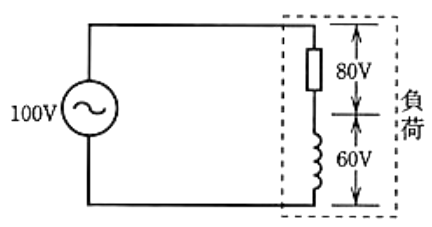
イ. 43 ロ. 57 ハ. 60 二. 80
電流を基準としたベクトル図を示します。
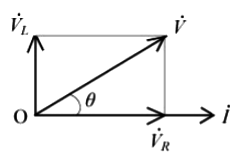
ベクトル図より、力率 $cosθ$[%]は、
$cosθ=\displaystyle\frac{V_R}{V}×100$
$=\displaystyle\frac{V_R}{\sqrt{{V_R}^2+{V_L}^2}}×100$
$=\displaystyle\frac{80}{\sqrt{80^2+60^2}}×100=80$[%]
答え(二)
2007年(平成19年)問3
2013年(平成25年)上期 問3
2014年(平成26年)上期 問3 類似
2016年(平成28年)下期 問4 類似
2017年(平成29年)上期 問2 類似
問12 交流の電力と力率④
図のような回路で、抵抗に流れる電流が 6[A]、リアクタンスに流れる電流が 8[A]であるとき、回路の力率[%]は。
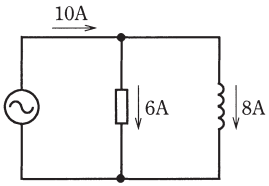
イ. 43 ロ. 60 ハ. 75 二. 80
電圧を基準としたベクトル図を示します。
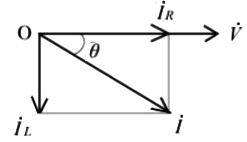
ベクトル図より、力率 $cosθ$[%]は、
$cosθ=\displaystyle\frac{I_R}{I}×100$
$=\displaystyle\frac{I_R}{\sqrt{{I_R}^2+{I_L}^2}}×100$
$=\displaystyle\frac{6}{\sqrt{6^2+8^2}}×100=60$[%]
答え(ロ)
2010年(平成22年)問4
2015年(平成27年)上期 問2
問13 交流の電力と力率⑤
図のような交流回路で、負荷に対してコンデンサCを設置して、力率 100[%]に改善した。このときの電流計の指示値は。
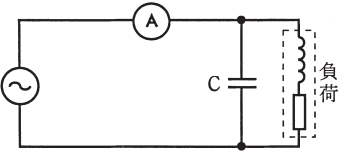
- 零になる。
- コンデンサ設置前と比べて増加する。
- コンデンサ設置前と比べて減少する。
- コンデンサ設置前と比べて変化しない。
電圧を $V$[V]、電流を $I$[A]、力率 $cosθ$ の交流回路の消費電力 $P$[W]は、
$P=VIcosθ$[W]
$I=\displaystyle\frac{P}{Vcosθ}$[A]
電流は、力率 $cosθ$に反比例します。つまり、$cosθ=100$[%]( $cosθ=1$)のとき、電流は最小となります。
答え(ハ)
2006年(平成18年)問3
2009年(平成21年)問5
2013年(平成25年)上期 問4
2015年(平成27年)上期 問4
2017年(平成29年)上期 問4
問14 交流の電力と力率⑥
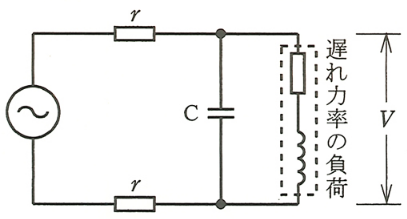
図のように、遅れ力率の負荷に対してコンデンサCを設置して、力率を 100[%]に改善した。このときの負荷両端の電圧 $V$ は。
ただし、rは電線の抵抗である。
- コンデンサ設置前と比べて高くなる。
- コンデンサ設置前と比べて低くなる。
- コンデンサ設置前と比べて変化しない。
- 零になる。
電圧を $V$[V]、電流を $I$[A]、力率 $cosθ$ の交流回路の消費電力 $P$[W]は、
$P=VIcosθ$[W]
$I=\displaystyle\frac{P}{Vcosθ}$[A]
電流は、力率 $cosθ$に反比例します。つまり、$cosθ=100$[%]( $cosθ=1$)のとき、電流は最小となります。
力率を改善することで、流れる電流は少なくて済むことになりますので、負荷の両端の電圧は上がります。
答え(イ)
2011年(平成23年)下期 問4
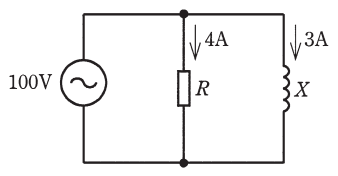
問15 消費電力
図のような回路で、抵抗 $R$ に流れる電流が 4[A]、リアクタンス $X$ に流れる電流が 3[A]であるとき、この回路の消費電力[W]は。
イ. 300 ロ. 400 ハ. 500 二. 700
電圧を基準としたベクトル図を示します。

ベクトル図より、電流 $I$[A]及び力率 $cosθ$ は、
$I=\sqrt{{I_R}^2+{I_L}^2}=\sqrt{4^2+3^2}=\sqrt{25}=5$[A]
$cosθ=\displaystyle\frac{I_R}{I}=\displaystyle\frac{4}{5}=0.8$
消費電力 $P$[W]は、
$P=VIcosθ=100×5×0.8=400$[W]
答え(ロ)
2012年(平成24年)上期 問2



