電験三種の法規で出題される需要率・不等率・負荷率について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の試験で、実際に出題された過去問題も解説しています。
需要率
需要率は、最大需要電力と設備容量の合計との比のことで、次式で表すことができます。
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
一般的に電気設備は、その設備容量いっぱいに負荷をかけることは少なく、負荷電力は設備容量より小さいのが普通です。需要率は、その程度を表すために用いられています。尚、測定する期間や季節により異なった値を示します。
不等率
不等率は、総合負荷において、個々の負荷に発生する最大需要電力を時刻に無関係に合計した値と合成最大需要電力との比のことで、次式で表すことができます。
$ 不等率=\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }$
個々の負荷は、それぞれの特性に応じて変化するため、その最大需要電力は同時刻に起こるものではありません。不等率は、その程度を表すために用いられています。不等率は常に1より大きく、この値が大きいほど一定の供給設備で大きな負荷設備に電力を供給することができます。つまり、不等率の大きいことは、供給設備の利用率の高いことを意味します。需要家相互間のほかにも、配電用変圧器や配電幹線相互間の不等率もあります。
なかなか分かりにくいかとは思いますが、負荷率、需要率と組み合わせた問題として出題されることが多々ありますので、意味合いをしっかりと理解するようにしましょう。
負荷率
負荷率は、ある期間内の平均電力と最大需要電力との比のことで、次式で表すことができます。
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
負荷率は、ある期間における負荷の変動状況、つまり負荷の特性や設備の利用度を表す指数です。供給種別や用途別によって固有の値を示します。一般に、高負荷率の需要の負荷曲線は、平均負荷に対して著しく変動することが少なく平たんな形をしています。低負荷率の需要の負荷曲線は、最大負荷と最低負荷との差が大きく負荷の変動幅が大きくなります。尚、期間のとり方によって日負荷率、月負荷率、年負荷率、などがあります。
電験三種-法規(施設管理)過去問題
1997年(平成9年)問10
受電場所における負荷率、需要率及び複数負荷間の不等率を次のA~Eの諸元で表したものの組み合わせで、正しいのは(1)~(5)のうちどれか。
A:設備容量
B:最大需要電力(最大負荷)
C:平均需要電力(平均負荷)
D:合成最大需要電力(合成最大負荷)
E:各負荷の最大需要電力の合計
| 負荷率 | 需要率 | 不等率 | |
| (1) | B/C | C/A | E/D |
| (2) | B/C | B/A | D/E |
| (3) | C/B | C/A | D/E |
| (4) | C/B | B/A | E/D |
| (5) | C/B | C/A | E/D |
1997年(平成9年)問10 過去問解説
負荷率、需要率、不等率は次の式で表すことができます。
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
$ 不等率=\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }$
答え (4)
2000年(平成12年)問11
図のような負荷曲線を持つA工場及びB工場があるとき、次の(a)及び(b)に答えよ。
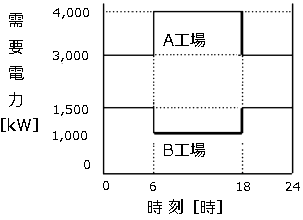
(a) A及びB両工場の需要電力の不等率の値として、正しいのは次のうちどれか。
(1) 0.9 (2) 1.0 (3) 1.1 (4) 1.2 (5) 1.3
(b) A及びB両工場の総合負荷率[%]の値として、正しいのは次のうちどれか。
(1) 91 (2) 92 (3) 93 (4) 94 (5) 95
2000年(平成12年)問11 過去問解説
(a) 不等率は次の式で表すことができます。
$ \begin{eqnarray}不等率&=&\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }\\\\&=&\displaystyle \frac{ 1500+4000 }{ 5000 }\\\\&=&1.1\end{eqnarray}$
答え (3)
(b) 負荷率は次の式で表すことができます。
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
平均電力は、(A工場の合計電力量+B工場の合計電力量)÷24h ですので、
A工場の合計電力量=3000×12+4000×12=84000
B工場の合計電力量=1500×12+1000×12=30000
$ \begin{eqnarray}平均電力&=&\displaystyle \frac{ 84000+30000 }{ 24 }\\\\&=&4750[kW]\end{eqnarray}$
$ 負荷率=\displaystyle \frac{ 4750 }{ 5000 }×100=95[%]$
答え (5)
2003年(平成15年)問8
次の文章は、複数の需要家を総合した場合の負荷率(以下。「総合負荷率」という。)と各需要家の需要率及び需要家間の不等率との関係についての記述である。これらの記述のうち、正しいのは次のうちどれか。
ただし、この期間中の各需要家の需要率はすべて等しいものと仮定する。
- 総合負荷率は、需要率に反比例し、不等率に比例する。
- 総合負荷率は、需要率には関係なく、不等率に比例する。
- 総合負荷率は、需要率及び不等率の両方に比例する。
- 総合負荷率は、需要率に比例し、不等率に反比例する。
- 総合負荷率は、需要率に比例し、不等率には関係しない。
2003年(平成15年)問8 過去問解説
不等率=最大電力の和/最大電力
需要率=最大電力/設備電力
負荷率=平均電力/最大電力
負荷率は最大電力が分母にあるので、分子に最大電力のある需要率に反比例し、同じく分母に最大電力がある不等率に比例することになります。
答え (1)
2004年(平成16年)問12
AとBの二つの変電所を持つ工場がある。ある期間において、A変電所は負荷設備の定格容量の合計が 500[kW]、需要率 90[%]、負荷率 60[%]で、B変電所は負荷設備の定格容量の合計が 300[kW]、需要率 80[%]、負荷率 50[%]であった。二つの変電所間の不等率が 1.3 であるとき、次の(a)及び(b)に答えよ。
(a) 工場の合成最大需要電力[kW]の値として、最も近いのは次のうちどれか。
(1) 346 (2) 450 (3) 531 (4) 615 (5) 690
(b) 工場を総合したこの期間の負荷率[%]の値として、最も近いのはつぎのうちどれか。
(1) 55.0 (2) 56.5 (3) 63.4 (4) 73.5 (5) 86.7
2004年(平成16年)問12 過去問解説
(a) 需要率と不等率から導きます。A変電所の最大需要電力は、
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
$ 90=\displaystyle \frac{ 最大需要電力 }{ 500 }×100[%]$
A変電所の最大需要電力は 450[kW]になります。同様に計算すると、B変電所の最大需要電力は 240[kW]になります。「各負荷の最大需要電力の合計=A変電所の最大需要電力+B変電所の最大需要電力」 ですので、
$ 不等率=\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }$
$ 合成最大需要電力=\displaystyle \frac{ 450+240 }{1.3}=531[kW]$
答え (3)
(b) 負荷率は、
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
総平均需要電力 $P_{av}$ は、各変電所の平均電力の和ですので、
$ P_{av}= 500×0.9×0.6+300×0.8×0.5 =390[kW]$
工場を総合したこの期間の負荷率[%]は、
$ 負荷率=\displaystyle \frac{ 390 }{ 531 }×100=73.5[%]$
答え (4)
2006年(平成18年)問10
配電系統及び需要家設備における供給設備と負荷設備との関係を表す係数として、需要率、不等率、負荷率があり、
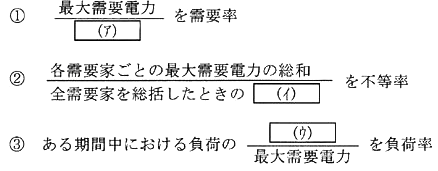
上記の記述の空欄箇所(ア),(イ)及び(ウ)に当てはまる語句として、正しいものを組合せたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 総負荷設備容量 | 合成最大需要電力 | 平均需要電力 |
| (2) | 合成最大需要電力 | 平均需要電力 | 総負荷設備容量 |
| (3) | 平均需要電力 | 総負荷設備容量 | 合成最大需要電力 |
| (4) | 総負荷設備容量 | 平均需要電力 | 合成最大需要電力 |
| (5) | 変圧器設備容量 | 総負荷設備容量 | 平均需要電力 |
2006年(平成18年)問10 過去問解説
需要率、不等率、負荷率は次の式で表すことができます。
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
$ 不等率=\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }$
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
答え (1)
2008年(平成20年)問12
ある変電所から供給される下表に示す需要家A,B及びCがある。各需要家間の負荷の不等率を 1.2 とするとき、次の(a)及び(b)に答えよ。
| 需要家 | 負荷の設備容量 [kV・A] | 力率 | 需要率 [%] | 負荷率 [%] |
| A | 500 | 0.90 | 40 | 50 |
| B | 200 | 0.85 | 60 | 60 |
| C | 600 | 0.80 | 60 | 30 |
(a) 需要家Aの平均電力[kW]の値として、最も近いのは次のうちどれか。
(1) 61.2 (2) 86.4 (3) 90 (4) 180 (5) 225
(b) 変電所からみた合成最大需要電力[kW]の値として、最も近いのは次のうちどれか。
(1) 198 (2) 285 (3) 325 (4) 475 (5) 684
2008年(平成20年)問12 過去問解説
(a) 負荷率から需要家Aの平均電力[kW]を求めます。
$ 負荷率=\displaystyle \frac{ 平均電力 }{ 最大需要電力 }×100[%]$
$ 50=\displaystyle \frac{ 平均電力 }{ 500×0.9 }×100[%]$
$平均電力=500×0.9×0.4×0.5 =90[kW]$
答え (3)
(b) 需要家A,B及びCの 最大需要電力を需要率より求めます。
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
需要家A:$500×0.90×0.4=180[kW]$
需要家B:$200×0.85×0.6=102[kW]$
需要家C:$600×0.80×0.6=288[kW]$
最大重要電力の和は、
$180+102+288 =570[kW]$
変電所からみた合成最大需要電力[kW]は、
$ 不等率=\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }$
$ 1.2=\displaystyle \frac{ 570 }{ 合成最大需要電力 }$
$合成最大需要電力=\displaystyle \frac{ 570 }{ 1.2 }=475[kW]$
答え (4)
2011年(平成23年)問12
ある変電所において、図のような日負荷特性を有する三つの負荷群A,B及びCに電力を供給している。 この変電所に関して、次の(a)及び(b)の問に答えよ。
ただし、負荷群A,B及びCの最大電力は,それぞれ 6500[kW],4000[kW]及び 2000[kW]とし、また、 負荷群A,B及びCの力率は時間に関係なく一定で、それぞれ 100[%],80[%]及び 60[%]とする。
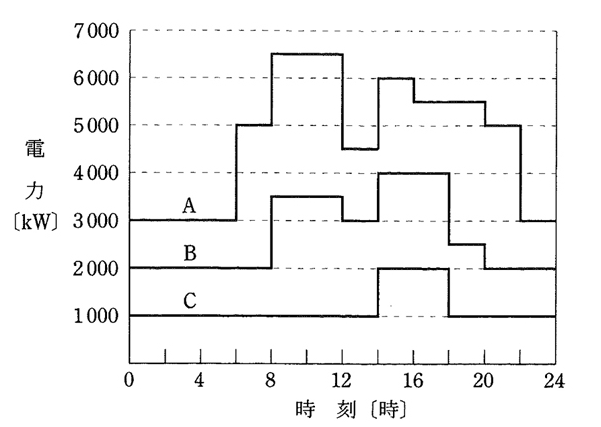
(a) 不等率の値として、 最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.98 (2) 1.00 (3) 1.02 (4) 1.04 (5) 1.06
(b) 最大負荷時における総合力率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 86.9 (2) 87.7 (3) 90.4 (4) 91.1 (5) 94.1
2011年(平成23年)問12 過去問解説
(a) 不等率は次の式で表すことができます。
$\begin{eqnarray}不等率&=&\displaystyle \frac{ 各負荷の最大需要電力の合計 }{ 合成最大需要電力 }\\\\&=&\displaystyle \frac{ 6500+4000+2000 }{ 6000+4000+2000 }\\\\&=&1.04\end{eqnarray}$
答え (4)
(b) 14時から16時の最大負荷時の有効電力と無効電力は、次の表のようになります。
| 負荷 | 有効電力 | 無効電力 | 力率 |
| A | 6000[kW] | 0[kvar] | 100[%] |
| B | 4000[kW] | 3000[kvar] | 80[%] |
| C | 2000[kW] | 2667[kvar] | 60[%] |
| 合計 | 12000[kW] | 5667[kvar] | 90.4[%] |
$合成負荷の力率=\displaystyle \frac{ 12000}{\sqrt{12000^2+5667^2} }=90.4$
答え (3)
2014年(平成26年)問12
ある事業所内におけるA工場及びB工場の、それぞれのある日の負荷曲線は図のようであった。それぞれの工場の設備容量が、A工場では 400kW、B工場では 700kWであるとき、次の(a)及び(b)の問に答えよ。
(a) A工場及びB工場を合わせた需要率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 54.5 (2) 56.8 (3) 63.6 (4) 89.3 (5) 90.4
(b) A工場及びB工場を合わせた総合負荷率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 56.8 (2) 63.6 (3) 78.1 (4) 89.3 (5) 91.6
2014年(平成26年)問12 過去問解説
(a) A工場及びB工場を合計した最大需要電力を考えます。
0時から 6時:600+100=700[kW]
6時から12時:200+300=500[kW]
12時から18時:200+400=600[kW]
18時から24時:100+600=700[kW]
したがって、最大需要電力は 700[kW]になります。A工場及びB工場を合わせた需要率[%]は、
$ 需要率=\displaystyle \frac{ 最大需要電力 }{ 設備容量の合計 }×100[%]$
$ 需要率=\displaystyle \frac{ 700 }{ 400+700 }×100=63.6[%]$
答え (3)
(b) A工場とB工場を合成した平均電力は、
$ 平均電力=\displaystyle \frac{ 700+500+600+700 }{ 4 }=625[kW]$
A工場及びB工場を合わせた総合負荷率の値[%]は、
$ 負荷率=\displaystyle \frac{ 625 }{ 700 }×100=89.3[%]$
答え (4)





