第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される電気の単位と抵抗温度係数について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された電気の単位と抵抗温度係数の過去問題も解説しています。
電気及び磁気に関する量とその単位記号の一覧
| 量 | 記号 | SI単位 | MKS単位 | 定義 |
| 電流 | $I$ | アンペア[A] | アンペア[A] | $I=\displaystyle\frac{ΔQ}{Δt}$ |
| 電荷、電気量 | $Q$ | クーロン[C] | クーロン[C] | |
| 電界の強さ | $E$ | ボルト毎メートル[V/m] | ボルト毎メートル[V/m] | $E=\displaystyle\frac{F}{Q}$ |
| 電位 | $V$ | ボルト[V] | ボルト[V] | |
| 電位差、電圧 | $U$、$(V)$ | ボルト[V] | ボルト[V] | |
| 起電力 | $E$ | ボルト[V] | ボルト[V] | |
| 電束密度 | $D$ | クーロン毎平方メートル[C/㎡] | クーロン毎平方メートル[C/㎡] | |
| 電束 | $Ψ$ | クーロン[C] | クーロン[C] | $Ψ=DA$ |
| 静電容量 | $C$ | ファラド[F] | ファラド[F] | $C=\displaystyle\frac{Q}{U}$ |
| 誘電率 | $ε$ | ファラド毎メートル[F/m] | ファラド毎メートル[F/m] | |
| 磁界の強さ | $H$ | アンペア毎メートル[A/m] | アンペアターン毎メートル[AT/m] | |
| 磁束密度 | $B$ | テスラ[T] | ウェーバ毎平方メートル[Wb/㎡] | $1T=1Wb/㎡$ |
| 磁束 | $φ$ | ウェーバ[Wb] | ウェーバ[Wb] | |
| 自己インダクタンス | $L$ | ヘンリー[H] | ヘンリー[H] | $L=\displaystyle\frac{φ}{I}$ |
| 相互インダクタンス | $M$、$L_{12}$ | ヘンリー[H] | ヘンリー[H] | $M=\displaystyle\frac{φ_1}{I_2}$ |
| 透磁率 | $μ$ | ヘンリー毎メートル[H] | ヘンリー毎メートル[H] | $μ=\displaystyle\frac{B}{H}$ |
| 抵抗(直流) | $R$ | オーム[Ω] | オーム[Ω] | $R=\displaystyle\frac{V}{I}$ |
| コンダクタンス(直流) | $G$ | ジーメンス[S] | モー[$Ω^{-1}$] | $G=\displaystyle\frac{1}{R}$ |
| 抵抗率 | $ρ$ | オームメートル[Ω・m] | オームメートル[Ω・m] | $ρ=\displaystyle\frac{E}{J}$ |
| 導電率 | $σ$ | ジーメンス[S/m] | ジーメンス[S/m] | $σ=\displaystyle\frac{1}{ρ}$ |
| 磁気抵抗 | $R_m$ | 毎ヘンリー[$H^{-1}$] | アンペア毎ウェーバ[A/Wb] | $R=\displaystyle\frac{U_m}{φ}$ |
| 位相差 | $θ$ | ラジアン[rad] | ラジアン[rad] | |
| インピーダンス | $Z$ | オーム[Ω] | オーム[Ω] | |
| リアクタンス | $X$ | オーム[Ω] | オーム[Ω] | |
| アドミタンス | $Y$ | ジーメンス[S] | モー[$Ω^{-1}$] | |
| サセプタンス | $B$ | ジーメンス[S] | モー[$Ω^{-1}$] | |
| 有効電力 | $P$ | ワット[W] | ワット[W] | |
| 無効電力 | $Q$ | バール[var] | ||
| 皮相電力 | $S$ | ボルトアンペア[VA] | ||
| 電力量 | $W_p$ | ジュール[J] ワット秒[W・s] | ジュール[J] ワット秒[W・s] | 1J=1W・s |
温度上昇により抵抗値の変化を表す公式
導体は温度を上げると電気抵抗が大きくなります。温度上昇により次の式のように、抵抗値は変化します。
温度上昇により抵抗値の変化を表す公式
$R_2=R_1(1+α_1(t_2-t_1))$
$R_1$[Ω]:$T_1$[℃]における抵抗値
$R_2$[Ω]:$T_2$[℃]における抵抗値
$α$[℃-1]:基準温度 $T_1$[℃]における抵抗温度係数
電験三種-理論の過去問解説:電気の単位と抵抗温度係数
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1999年(平成11年)問1【電験理論の過去問題】
電気及び磁気に関する量とその単位記号(これと同じ内容を表す単位記号を含む)の組み合わせとして、誤っているものは次のうちどれか。
(1) 電界の強さ V/m (2) 磁束 T (3) 電力量 W・S (4)磁気抵抗 H-1 (5) 電流 C/s
(2)の磁束の単位はWb(ウェーバ)で、T(テスラ)は磁束密度Bの単位です。
答え (2)
2011年(平成23年)問5【電験理論の過去問題】
20[℃]における抵抗値が $R_1$[Ω]、抵抗温度係数が $α_1$[$℃^{-1}$]の抵抗器Aと 20[℃]における抵抗値が $R_2$[Ω]、抵抗温度係数が $α_2$=0[$℃^{-1}$]の抵抗器Bが並列に接続されている。その 20[℃]と 21[℃]における並列抵抗値をそれぞれ $r_{20}$[Ω]、$r_{21}$[Ω]とし、$\displaystyle\frac{r_{21}-r_{20}}{r_{20}}$を変化率とする。変化率として、正しいものを次の(1)~(5)のうちから一つ選べ。
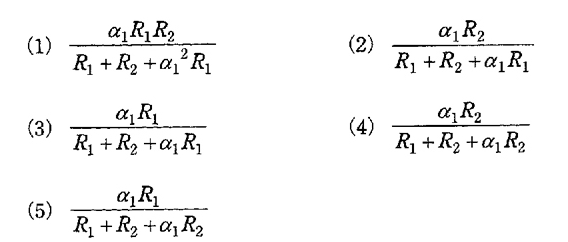
温度上昇により抵抗値の変化を表す公式は次のとおりです。
$R_2=R_1(1+α_1(t_2-t_1))[Ω]$
αは、抵抗温度係数で、単位は$[℃^{-1}]$
20[℃]における並列抵抗値 r20[Ω]は、
$r_{20}=\displaystyle\frac{R_1R_2}{R_1+R_2}$
21[℃]に温度上昇後の抵抗値を、$R_1’$, $R_2’$ とすると、
$\begin{eqnarray}R_1’&=&R_1(1+α_1(21-20))\\\\&=&R_1(1+α_1)[Ω]… (1)\end{eqnarray} $
$R_2’=R_2(1+α_2(21-20))=R_2[Ω]… (2)$
21[℃]における並列抵抗値は r21[Ω]は、
$r_{21}=\displaystyle\frac{R_1’R_2′}{R_1’+R_2′} … (3)$
(3)式に(1),(2)式を代入します。
$r_{21}=\displaystyle\frac{R_1’R_2′}{R_1’+R_2′}=\displaystyle\frac{R_1(1+α_1)R_2}{R_1(1+α_1)+R_2}$
求める変化率は、
$\begin{eqnarray}\displaystyle\frac{r_{21}-r_{20}}{r_{20}}&=&\frac{\displaystyle\frac{R_1(1+α_1)R_2}{R_1(1+α_1)+R_2}-\displaystyle\frac{R_1R_2}{R_1+R_2}}{\displaystyle\frac{R_1R_2}{R_1+R_2}}\\\\&=&\frac{(1+α_1)(R_1+R_2)}{R_1(1+α_1)+R_2}-1\\\\&=&\frac{α_1R_2}{R_1+R_1α_1+R_2}\end{eqnarray}$
答え (2)
2011年(平成23年)問14【電験理論の過去問題】
電気及び磁気に関する量とその単位記号(他の単位による表し方を含む)との組み合わせとして、誤っているものを次の(1)~(5)のうちから一つ選べ。
| 量 | 単位記号 | |
| (1) | 導電率 | S/m |
| (2) | 電力量 | W・s |
| (3) | インダクタンス | Wb/V |
| (4) | 磁束密度 | T |
| (5) | 誘電率 | F/m |
(3)のインダクタンスの単位はH(ヘンリー)です。
答え (3)
2015年(平成27年)問7【電験理論の過去問題】
以下の記述で、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 直流電圧源と抵抗器、コンデンサが直列に接続された回路のコンデンサには、定常状態では電流が流れない。
- 直流電圧源と抵抗器、コイルが直列に接続された回路のコイルの両端の電位差は、定常状態では零である。
- 電線の抵抗値は、長さに比例し、断面積に反比例する。
- 並列に接続した二つの抵抗器R1,R2を一つの抵抗器に置き換えて考えると、合成抵抗の値はR1,R2の抵抗値の逆数の和である。
- 並列に接続した二つのコンデンサC1,C2を一つのコンデンサに置き換えて考えると、 合成静電容量はC1,C2の静電容量の和である。
並列回路の合成抵抗値は、和分の積です。したがって(4)が誤りです。
答え (4)
2016年(平成28年)問8【電験理論の過去問題】
電気に関する法則の記述として、正しいものを次の(1)~(5)のうちから一つ選べ。
- オームの法則は、「均一の物質から成る導線の両端の電位差をVとするとき、これに流れる定常電流IはVに反比例する」という法則である。
- クーロンの法則は、「二つの点電荷の間に働く静電力の大きさは、両電荷の積に反比例し、電荷間の距離の2乗に比例する」という法則である。
- ジュールの法則は「導体内に流れる定常電流によって単位時間中に発生する熱量は、電流の値の2乗と導体の抵抗に反比例する」という法則である。
- フレミングの右手の法則は、「右手の親指・人差し指・中指をそれぞれ直交するように開き、親指を磁界の向き、人差し指を導体が移動する向きに向けると、中指の向きは誘導起電力の向きと一致する」という法則である。
- レンツの法則は、「電磁誘導によってコイルに生じる起電力は、誘導起電力によって生じる電流がコイル内の磁束の変化を妨げる向きとなるように発生する」という法則である。
(5) レンツの法則は、「電磁誘導によってコイルに生じる起電力は、誘導起電力によって生じる電流がコイル内の磁束の変化を妨げる向きとなるように発生する」という法則です。
答え (5)
2017年(平成29年)問14【電験理論の過去問題】
次の(1)~(5)は、計測の結果、得られた測定値を用いた計算である。これらのうち、有効数字と単位の取り扱い方がともに正しいものを一つ選べ。
- 0.51V+2.2V=2.71V
- 0.670V÷1.2A=0.558Ω
- 1.4A×3.9ms=5.5×10-6C
- 0.12A-10mA=0.11m
- 0.5×2.4F×0.5V×0.5V=0.3J
- 0.51Vは有効数字2桁、2.2Vは有効数字2桁。答えの2.71Vは有効数字2桁で表す必要がありますので、誤りです。
- 0.670Vは有効数字3桁、1.2Aは有効数字2桁。答えの0.558Ωは有効数字2桁で表す必要がありますので、誤りです。
- 単位の[A]×[ms]=[mC]ですので、$10^{-3}C$ になりますので、誤りです。
- 単位の[A]-[mA]は、[A]または[mA]になりますので、誤りです。
- 有効数字と単位の取り扱い方がともに正しい
答え(5)
電験三種の理論科目に出題される「電気電子工学(電気の現象)」のページ
1.電気の単位と抵抗温度係数
2.電界中の電子の運動
3.ローレンツ力の向きと円運動
4.電子放出と熱起電力の原理
5.過渡現象と時定数とは






