これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「負荷と力率」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。
電気的負荷 (R,L,C )
電気的負荷の種類には、電熱器、蛍光灯、電動機などいろいろのものがありますが、これら負荷を電気的にみると抵抗 ( $R$ )、インダクタンス( $L$ )、静電容量 ( $C$ )の合成された回路とみなすことができます。 これら $R,L,C$ に交流電圧 $v=\sqrt{2}sinωt$〔V〕を加えた場合の電気的性質を調べてみます。
抵抗Rだけの回路 (第1図 )
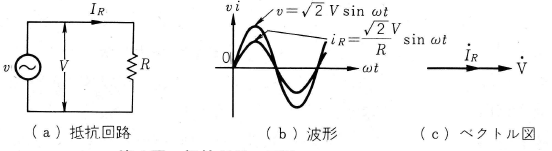
抵抗 $R$〔Ω〕に交流電圧 $V$〔V〕 を加えると、流れる電流 $I_R$ (実効値)は、
$I_R=\displaystyle \frac{V}{R}$〔A〕
となります。電圧とは同相です。
イ ンダクタンスLだけの回路(第2図 )
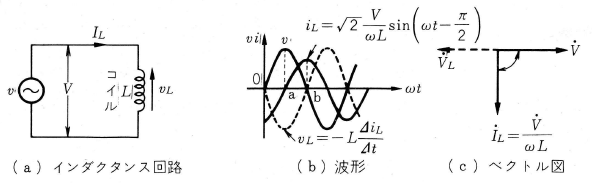
インダクタンス $L$〔H(ヘンリー)〕のコイルに交流電圧を加えると、電流が流れようとしますが、コイルには電磁誘導作用により電流の変化 (磁束 $φ$ の変化)をさまたげるような逆起電力 $v_L$ を生じます。
そこで、(b)図に示すような交流電流 $i_L$ が $L$ に流れた場合の $i_L$ と $v_L$ の関係を調べると、$v_L$ は $i_L$ の時間的変化の割合に比例しますので、図の a 点では $i_L$ の変化が最大で $v_L$ も最大、b点では $i_L$ の変化は零であるから $v_L$ も零となります。このように電流の各点に対し調べると $v_L$ は (b)図のように $i_L$ より90°位相の遅れた正弦波電圧となります。したがって、コイルに電流を流し続けるには、この逆起電力 $v_L$ を打ち消すような $v_L$ と反対位相の電圧、つまり $i_L$より90°進んだ電源電圧 $v$ が必要となります。
$L$ に流れる電流の大きさ $I_L$ (実効値)は、回路方程式を解くと、
$I_L=\displaystyle \frac{V}{2πfL}$〔A〕
で表わすことができます。$2πfL=ωL=X_L$ は、誘導性リアクタンスといい、単位は抵抗と同じく〔Ω〕です。
静電容量 (C)だけの回路 (第3図 )
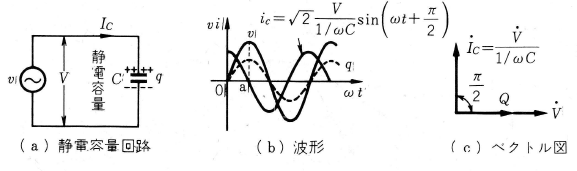
コンデンサ $C$ には、電気 (電荷 $q$ )を蓄えたり、放出したりする充放電作用があり、流れる電流は $C$ に
加わる電圧の時間的変化 ( $q$ の変化)に比列します。いま、静電容量 $C$〔 F(ファラド)〕のコンデンサに、交流電圧 $v$ を加えた場合、$C$ に流れる電流 $i_C$ を(b)図で調べます。
図において、$v$ が0点より上昇しようとすると、この点では ( $\displaystyle \frac{Δv}{Δt}$ )が 最大であるから、$i_c$ は最大、$v$ がさらに上昇してa点に達すると( $\displaystyle \frac{Δv}{Δt}$ )が零となり、 $i_c$ も零となります。$v$ がa点より下降を始めると $\displaystyle \frac{ Δv}{Δt}$ は負となるので $i_c$ も負となり、$C$ に蓄えた電気を逆方向の放電電流として放出します。$v$ の各点に対してこれを調べると、$i_c$ は電源電圧 $v$ より90°進んだ正弦波交流電流となり、流れる電流の実効値 $I_c$ は、
$I_c=\displaystyle \frac{ V}{\left(\displaystyle \frac{ 1}{2πfC}\right)}$〔A〕
で表わすことができます。$\displaystyle \frac{ 1}{2πfC}=\displaystyle \frac{ 1}{ωC}=X_C$ は、容量性リアクタンスといい、単位は〔Ω〕です。
R,L,Cの合成回路と力率
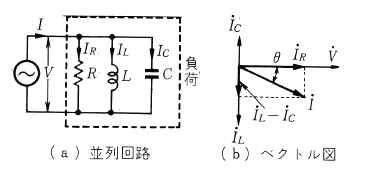
第4図のように、$R,L,C$ の並列回路に、交流電圧 $V$〔V〕を加えると、回路を流れる電流のベクトル図は(b)図のようになります。図において、$\dot{V}$ と入力電流 $\dot{I}$ との位相角$θ$を負荷の力率角、$cosθ$ を負荷力率といいます (普通 $cosθ$ を百倍して%で表わす)。また、$\dot{V}$ より $\dot{I}$ が進んでいる場合を進み力率、 $\dot{V}$ より $\dot{I}$ が遅れている場合を遅れ力率といいます。
負荷の特性
電力を供給するものを電源、電力を使用するものが負荷です。負荷は電気的にみれば $R,L,C$ の合成回路とみなすことができますが、実際の電気機器において、これらがどのような構成になっているかを、蛍光灯を例にとって説明します。ここでその説明をする前に $R,L,C$ 回路の補足説明をしておきます。
R,L,Cの直列回路、インピーダンス
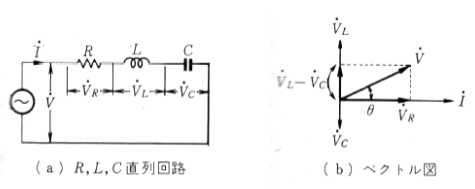
第5図のように $R,L,C$ を直列に接続し、交流電圧 $v=\sqrt{2}sinωt$〔V〕を加えた場合を調てみます。回路を流れる電流 $\dot{I}$ を基準にとり、$R,L,C$ 各素子の電圧降下をそれぞれ $\dot{V}_R$,$\dot{V}_L$,$\dot{V}_C$ として、ベクトル図を書けば、(b)図のようになります。
$\dot{V}=\dot{I}R$〔V〕で $\dot{I}$ と同相
$\dot{V_L}=ωL\dot{I}$〔V〕 で $\dot{I}$ より $\displaystyle \frac{ π}{2}$ 進み
$\dot{V_C}=\displaystyle \frac{\dot{I}}{ωC}$〔V〕で $\dot{I}$より$\displaystyle \frac{π}{2}$ 遅れ
であり、$\dot{V_R}$,$\dot{V_L}$,$\dot{V_C}$ をベクトル的に合成したものは電源電圧 $\dot{V}$ に等しくなります。ベクトル図より、
$V=\sqrt{(V_R)^2+(V_L-V_C)^2}$
となり、これを変形すると、
$V=\sqrt{(IR)^2+\left(ωLI-\displaystyle \frac{I}{ωC}\right)^2}=I\sqrt{(R)^2+\left(ωL-\displaystyle \frac{1}{ωC}\right)^2}$
となります。
ここで、$\sqrt{(R)^2+\left(ωL-\displaystyle \frac{1}{ωC}\right)^2}=\displaystyle \frac{V}{I} $を回路のインピーダ ンスといい $Z$ で表わします。$Z$ は回路の電流を規制する値であり、抵抗と同じく単位は〔Ω〕です。なお、$θ$ は力率角で、$θ=tan^{-1}\displaystyle \frac{(ωL-\displaystyle \frac{1}{ωC})}{R}$、負荷力率 $cosθ=\displaystyle \frac{R}{Z} $ で表わされます。
蛍光灯回路
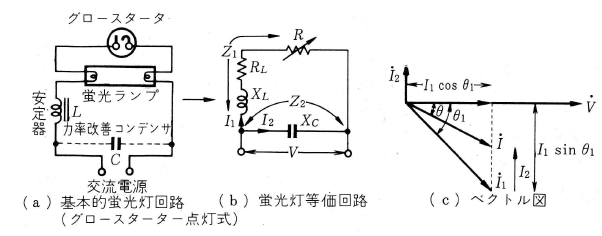
第6図 (a)に蛍光灯の基本構成を示しましたが、点灯時の蛍光灯回路を電気的にみれば (b)図のような等価回路となります。図で $X_L=ωL$〔Ω〕は安定器の誘導リアクタンス、$R_L$〔Ω〕は安定器の巻線抵抗損失および鉄損などの損失を等価的に抵抗で表わしたもの、$R$ は蛍光ランプの放電抵抗、$X_C=\displaystyle \frac{1}{ωC}$〔Ω〕は力率改善用コンデンサの容量リアクタンスです。蛍光ランプなどの放電管は、放電電流が増加するほど、ランプ放電抵抗 $R$ が減少する電気的負特性をもっており、安定器はランプ電流を一定にするために必要です。
この蛍光灯回路に交流電圧 $V$〔V〕を加えた場合、流れる電流、力率は次のようになります。
$I_1=\displaystyle \frac{V}{Z_1}=\displaystyle \frac{V}{\sqrt{(R_L+R)^2+(X_L)^2}}$〔A〕
$θ_1=tan^{-1}\displaystyle \frac{X}{(R+R_L)} $
$I_2=\displaystyle \frac{V}{Z_2}=\displaystyle \frac{V}{X_C}$〔A〕
で $V$ より $\displaystyle \frac{π}{2}$ 進み
これをベクトル図で示すと(b)図のようになります。したがって、入力電流 $\dot{I}$ は $\dot{I}=\dot{I}_1+\dot{I}_2$ で、
$I=\sqrt{(I_1cosθ_1)^2+(I_1sinθ_1-I_2)^2}$〔A〕
となり、
$θ=tan^{-1}\displaystyle \frac{(I_1sinθ_1― I_2)}{I_1cosθ_1}$
入力よりみた負荷力率は
$cosθ=\displaystyle \frac{I_1 cosθ_1}{I}$
となります。
負荷の特性を知るには
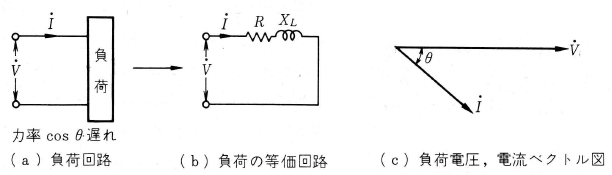
蛍光灯回路の $R,L,C$ 構成は比較的簡単でですが、負荷の種類によっては非常に複雑なものがあります。ところで、実際に電気機器を使用する場合、$R,L,C$ の構成がどのようになっているかということは、あまり必要ではなく、必要なのは入力よりみた電気的特性です。第7図 (a)に示すような、ある負荷があり、この負荷の定格電圧が $V$〔V〕、定格電流が $I$〔A〕、力率が遅れ $cosθ$ であったとすると、負荷回路の構成は等価的に(b)図のように表わされ、入力よりみたインピーダンス $Z=\displaystyle \frac{V}{I}$〔Ω〕、負荷抵抗 $R=Zcosθ$〔Ω〕、誘導リアクタンス $X_L=Zsinθ$〔Ω〕(進み力率の場合は容量リアクタンス $X_C$ )となります。
このように負荷をみる場合、定格電圧、電流、力率 (進み、遅 れ)、出力、起動電流などがわかれば、負荷の特性を十分に知ることができます。