第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「オシロスコープの周波数測定」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「オシロスコープの周波数測定」などの過去問題も解説しています。
ディジタル計器
ディジタル計器は、測定値を直流に変換しさらに、AーD変換器(アナログーディジタル変換器)を用いてパルスをカウントし、十進法による数字で不連続に表示する計器です。ディジタル計器には、コンピュータに接続して測定結果をコンピュータに入力できるものがあります。ディジタル計器には、次のような特徴があります。
- 入力インピーダンスが高く、被測定系への影響が小さい
- 高精度で測定でき、読み取り誤差が少ない
- 高度な処理が容易にできる
- 多くの測定項目を1台で測定できる
- 測定には電源が必要となる
オシロスコープ
オシロスコープは交流や過渡現象などのように時間的に変化する現象の波形を、ブラウン管面上に描いて観測する測定器です。
水平・垂直偏向電極
ブラウン管において蛍光面に投射する電子線の方向を変えるために信号を与える偏向回路において、水平あるいは垂直方向に偏向させるための電極です。垂直および水平の両偏向電極に、同相で同じ大きさの正弦波を加えると、オシロスコープ上には直線上のリサジュー図形が表示されます。
リサジュー図形
二つの正弦波をオシロスコープの水平軸と垂直軸に別々に加え、両者の周波数の比を整数比にすれば、両周波数比と位相差に応じた特有の図形が描かれます。このような図形をリサジュー図形といいます。
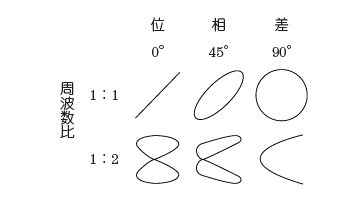
電験三種-理論の過去問解説:オシロスコープの周波数測定
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2000年(平成12年)問8【電験理論の過去問題】
オシロスコープを用いて電圧波形を観測する場合、垂直入力端子に正弦波電圧を加えると、垂直偏向電極にそれと同じ波形の電圧が加わり、水平偏向電極には内部で発生する( ア )電圧が加わるので、蛍光膜上に( イ )電圧の波形が表示される。
また、垂直及び水平の両入力端子に、同相で同じ大きさの正弦波を加えると( ウ )のリサジュー図形が蛍光膜上に表示される。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | のこぎり波 | 正弦波 | 直線状 |
| (2) | 正弦波 | のこぎり波 | 円 形 |
| (3) | 方形波 | のこぎり波 | 直線状 |
| (4) | 方形波 | 方形波 | だ円形 |
| (5) | のこぎり波 | 正弦波 | 円 形 |
オシロスコープを用いて電圧波形を観測する場合、垂直入力端子に正弦波電圧を加えると、垂直偏向電極にそれと同じ波形の電圧が加わり、水平偏向電極には内部で発生する( のこぎり波 )電圧が加わるので、蛍光膜上に( 正弦波 )電圧の波形が表示される。
また、垂直及び水平の両入力端子に、同相で同じ大きさの正弦波を加えると( 直線状 )のリサジュー図形が蛍光膜上に表示される。
答え (1)
2008年(平成20年)問16【電験理論の過去問題】
ブラウン管オシロスコープは、水平・垂直偏向電極を有し、波形観測ができる。次の(a)および(b)に答えよ。
(a)垂直偏向電極のみに、正弦波交流電圧を加えた場合は、蛍光面に( ア )のような波形が現れる。また、水平偏向電極のみにのこぎり波電圧を加えた場合は、蛍光面に( イ )のような波形が現れる。また、これらの電圧をそれぞれの電極に加えると、蛍光面に( ウ )のような波形が現れる。このとき波形を静止させて見るためには、垂直偏向電極の電圧の周波数と水平偏向電極の電圧の繰返し周波数との比が整数でなければならない。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
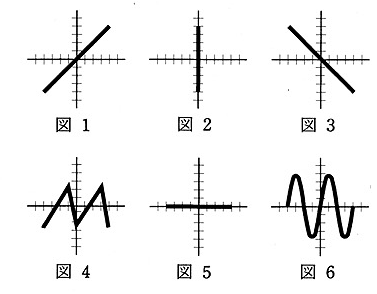
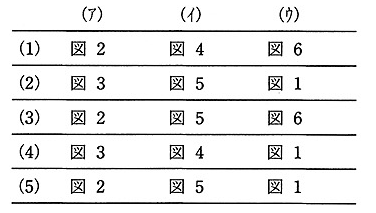
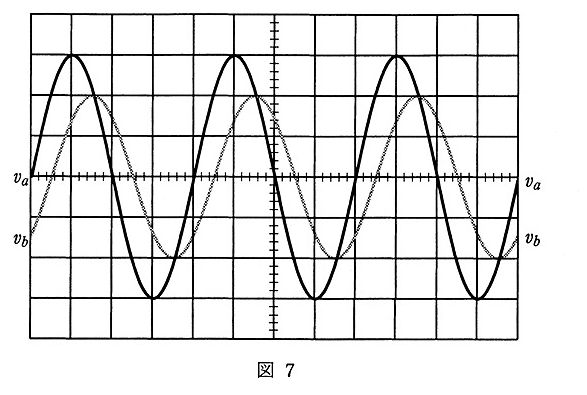
(b) 正弦波電圧 $v_a$ 及び $v_b$ をオシロスコープで観測したところ、蛍光面に図7に示すような電圧波形が現れた。同図から。$v_a$の実効値は( ア )[V]、$v_b$ の周波数は( イ )[kHz]、$v_a$の周期は( ウ )[ms]、$v_a$と$v_b$の位相差は( エ )[rad] であることが分かった。
ただし、オシロスコープの垂直感度は 0.1 [V]/div 、掃引時間は 0.2 [ms]/div とする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる最も近い値として、正しいものを組み合わせたのは次のうちどれか。

(a) 垂直偏向電極のみに、正弦波交流電圧を加えた場合は、蛍光面に( 図2 )のような波形が現れる。また、水平偏向電極のみにのこぎり波電圧を加えた場合は、蛍光面に( 図5 )のような波形が現れる。また、これらの電圧をそれぞれの電極に加えると、蛍光面に( 図6 )のような波形が現れる。このとき波形を静止させて見るためには、垂直偏向電極の電圧の周波数と水平偏向電極の電圧の繰返し周波数との比が整数でなければならない。
答え (3)
(b) 図に示します。
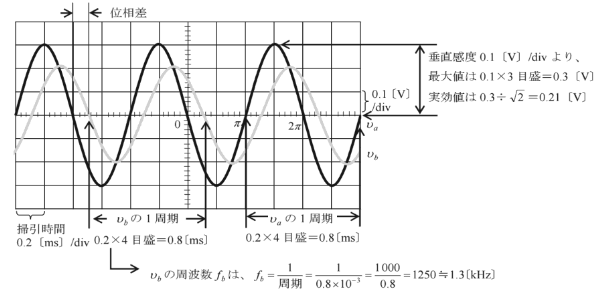
正弦波電圧 $v_a$ 及び $v_b$ をオシロスコープで観測したところ、蛍光面に図7に示すような電圧波形が現れた。同図から。$v_a$の実効値は( 0.21 )[V]、$v_b$ の周波数は( 1.3 )[kHz]、$v_a$の周期は( 0.8 )[ms]、$v_a$と$v_b$の位相差は( π/4 )[rad] であることが分かった。
ただし、オシロスコープの垂直感度は 0.1 [V]/div、掃引時間は 0.2 [ms]/divとする。
答え (1)
2013年(平成25年)問14【電験理論の過去問題】
ディジタル計器に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- ディジタル交流電圧計には、測定入力端子に加えられた交流電圧が、入力変換回路で直流電圧に変換され、次のA-D変換回路でディジタル信号に変換される方式のものがある。
- ディジタル計器では、測定量をディジタル信号で取り出すことができる特徴を生かし、コンピュータに接続して測定結果をコンピュータに入力できるものがある。
- ディジタルマルチメータは、スイッチを切り換えることで電圧、電流、抵抗などを測ることができる多機能測定器である。
- ディジタル周波数計には、測定対象の波形をパルス列に変換し、一定時間のパルス数を計数して周波数を表示する方式のものがある。
- ディジタル直流電圧計は、アナログ指示計器より入力抵抗が低いので、測定したい回路から計器に流れ込む電流は指示計器に比べて大きくなる。
(5)の記述はディジタルとアナログの特徴が反対に記述されています。したがって(5)が誤りです。
答え (5)
2013年(平成25年)問16【電験理論の過去問題】
振幅 Vm[V]の交流電源の電圧 v = Vmsinωt[V]をオシロスコープで計測したところ、画面上に図のような正弦波形が観測された。次の(a)及び(b)の問いに答えよ。ただし、オシロスコープの垂直感度は5[V]/div、掃引時間は2[ms]/divとし、測定に用いたプローブの減衰比は1対1とする。
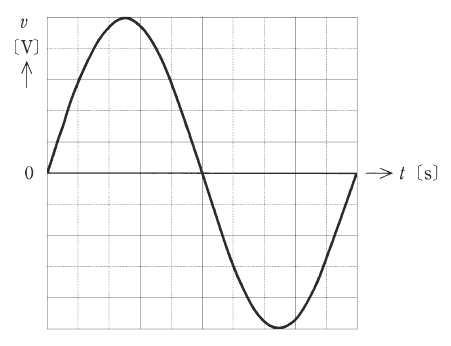
(a) この交流電源の電圧の周期[ms]、周波数[Hz]、実効値[V]の値の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
| 周期 | 周波数 | 実効値 | |
| (1) | 20 | 50 | 15.9 |
| (2) | 10 | 100 | 25.0 |
| (3) | 20 | 50 | 17.7 |
| (4) | 10 | 100 | 17.7 |
| (5) | 20 | 50 | 25.0 |
(b) この交流電源をある負荷に接続したとき $i=25cos(ωt-\displaystyle\frac{π}{3})$ の電流が流れた。この負荷の力率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 50 (2) 60 (3) 70.7 (4) 86.6 (5) 100
(a) 「div」は、1マスを意味します。よって、振幅 Vm [V] は5マス分、 周期 T [ms] は10マス分 ですので、
$V_m=5×5=25$[V]
$T=10×2=20$[ms]
周波数 f [Hz] は、
$f=\displaystyle\frac{1}{T}=\displaystyle\frac{1}{20×10^{-3}} =50$ [Hz]
また、実効値 V [V] は最大電圧の$\displaystyle\frac{1}{\sqrt{2}}$ 倍ですので、
$V=\displaystyle\frac{V_m}{\sqrt{2}} =\displaystyle\frac{25}{\sqrt{2}} =17.7$ [V]
答え (3)
(b) 瞬時値は v=25sinωt [V] で、負荷電流が $i=25cos(ωt-\displaystyle\frac{π}{3})$ ですので、sinとcosを変換すると、
$i=25cos(ωt-\displaystyle\frac{π}{3})$
$=25sin(ωt-\displaystyle\frac{π}{3}+ \displaystyle\frac{π}{2}) $
$=25sin(ωt+\displaystyle\frac{π}{6}) $
電圧との位相差が $+\displaystyle\frac{π}{6}$ [rad] ですので、その力率は、
$cos \displaystyle\frac{π}{6}=\displaystyle\frac{\sqrt{3}}{2}=0.866$
答え (4)
2016年(平成28年)問14【電験理論の過去問題】
ディジタル計器に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- ディジタル計器用のA-D変換器には、二重積分形が用いられることがある。
- ディジタルオシロスコープでは、周期性のない信号波形を測定することはできない。
- 量子化とは、連続的な値を何段階かの値で近似することである。
- ディジタル計器は、測定値が数字で表示されるので、読み取りの間違いが少ない。
- 測定可能な範囲(レンジ)を切り換える必要がない機能(オートレンジ)は、 測定値のおよその値が分からない場合にも便利な機能である。
ディジタルオシロスコープでは、周期性のない信号波形を測定することは可能です。したがって(2)が誤りです。
答え (2)
電験三種の理論科目に出題される「電気・電子計測分野」のページ
1.指示計器の種類と特徴
2.計測と測定誤差
3.電圧と電流の測定(倍率器と分流器)
4.抵抗の測定(電圧降下法・ダブルブリッジ法)
5.電力計の原理と二電力計法
6.オシロスコープの周波数測定




