電力量と発熱量【電気設備】

これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「電力量と発熱量」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。

電力
電力量
電力・電力量・発熱量
電動機のエネルギー変換
電力と冷暖房負荷

電力

単位時間になす仕事のことを仕事率といいますが、その場合の仕事が電気エネルギーによってなされたときの仕事率を電力といい、単位にはワット〔W〕を用います。

つまり、電力 $1$〔W〕とは、仕事率 $1$〔J/s〕のことで、$1$ 秒間に $1$ ジュールの仕事をする電気エネルギーを表わしています。なお、電力の単位として、ワットの $10^3$倍のkW、$10^6$倍のMWが用いられます。 (重力単位系では、$1$ kg重の力で $1$ m変位を生じたときの仕事は $1$〔kg・m〕で表わされ、この仕事が $1$ 秒間で行われたとき仕事率は $1$〔kg・ m/s〕であり、

$1$ 〔kg・ m/s〕$=g$〔N・m/s〕$=9.8$〔N・m/s〕 $=9.8$〔J/s〕$=9.8$〔W〕

に相当します ( $g$：重力の加速度〔$m/s^2$〕)。

電力量

電力量は、単位時間当りの仕事である電力と時間の積で表わされ、仕事量を表わします。電力量の単位はワット秒〔W・S〕ですが、実際に電力を使用する場合、ワット秒ではエネルギー単位が小さすぎるので、時間の単位として1時間〔H〕をとり、電力量をワットアワー〔WH〕、キロワットアワー〔kWH〕で表わすのが普通です。$1$〔kWH〕とは、$1$〔kW〕の電力を $1$ 時間使用したときの電力量であり、

$1$〔kWH〕$=1$〔kW〕$×1$〔H〕$= 1000$〔W〕$×3600$〔s〕$=3.6×10^6$〔ws〕=$3.6×10^6$〔J〕

つまり、$1$〔kWH〕は $3.6×10^6$〔J〕の電気エネルギーに相当します。電力と電力量は同じようなことばですが、内容的には大きな違いがあるので注意が必要です。

電力・電力量・発熱量

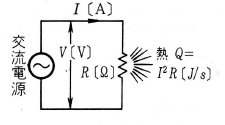
第1図に示すような抵抗回路に交流電圧 $V$〔V〕 (実効値)を加えると、回路には $I=\displaystyle \frac{V}{R}$〔A〕 (実効値)の電流が流れ、抵抗 $R$ にはジュールの法則により、$1$ 秒間に $I^2R$〔J〕のジュール熱が発生します。これは、電気エネルギーが抵抗 $R$ において $I^2R$〔J/s〕の熱として消費された、つまり単位時間に $I^2R$〔J〕の仕事をしたことを意味しています。したがって、電力の定義から、抵抗 $R$ で消費される電力は、 $P$ は、

$P=I^2R$〔J/s〕$=I^2R$〔w〕

となります。この電力 $P$ を $t$ 秒間使用する、つまり電流 $I$ を $t$ 秒間流し続けると、$P$ の消費電力量は、

$Pt$〔WS〕$=I^2Rt$〔ws〕

となり、この電力量は抵抗 $R$ において $I^2Rt$〔J〕のジュール熱になります。

また、オームの法則により $V=RI$ ですから、電力 $P$ を変形すると、

$P=I^2R=(IR)I=VI=\displaystyle \frac{V^2}{R}$ 〔W〕

と表わすことができ、電力量も $VIt$〔W・S〕と表わすことができます。

なお、熱の単位としてカロリー〔cal〕が使われることがありますが、$1$〔cal〕は $4.186$〔J〕に相当し、これを熱の仕事当量といいます。したがって、$1$〔W〕$=1$〔J/s〕は $\displaystyle \frac{1}{4.186}= 0.24$〔ca1/s〕の熱に相当し、$1$〔WS〕は $0.24$〔cal〕の発熱量となります。 $1$〔kWH〕の電力量を使用した場合の発生熱量を計算すると、

$1$〔kWH〕$=\displaystyle \frac{3.6×10^6}{4.186}=860×10^3=860$〔kcal〕

となり、$P$〔kW〕の電力を $1$ 時間使用すると $860P$〔kcal〕の熱量となります。

電動機のエネルギー変換

抵抗の場合、電力は $I^2R$〔J/s〕の熱エネルギーになりますが、電動機の場合はどうなるかを説明します。

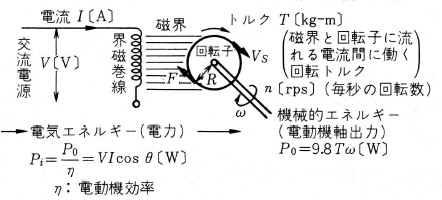
第2図において、電動機の界磁巻線に電流が流れ、磁界が発生し、この磁界により回転子はトルク $T$ を生じて、$n$〔rps〕の回転速度で回転します。このときの電動機軸出力 $Po$ (電動力)は

$Po=FVs=2πnFR=ωT$〔 kg・m/s〕$=9.8ωT$〔Nm/s〕$=9.8ωT$〔J/s〕$=9.8ωT$〔W〕
$R$：回転半径〔m〕、$F$：回転体に働く力〔kg〕、$Vs$：回転体線速度〔m/s〕、 $2πn=ω$：角速度〔rad/s〕

で表わされます。これは、$Pi$〔W〕の電力すなわち、電気エネルギーが、磁界を媒介として $Po=9.8ωT$〔W〕の機械的エネルギーに変換されたのであり、電動機効率を無視すれば $Pi=Po$ です。また、電動機軸出力 $1$〔kW〕$=1000/9.8$〔kgm/s〕で $1$ 時間運転するときの、機械エネルギーは、電力と同様、$860$〔kcal〕の熱量に相当します。

電力と冷暖房負荷

第3図に示すような一室があり、電熱器を用いて部屋の温度を24〔 ℃〕に暖房する場合の、電熱器
容量を次の条件の場合について求めてみます (その他の条件は無視する)。

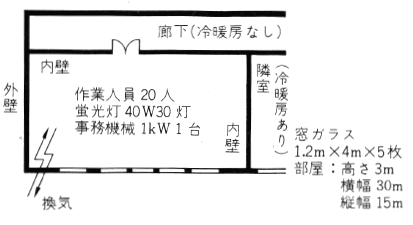
作業者の発生熱量：1人当り100〔kcal/h〕
照明の発生熱量：1〔kcal/W〕
部屋の換気は外気を取り入れるものとし, 換気量を100〔㎥/h〕とする
外気温3℃ ,空気の密度:1.2〔kg/㎥〕 , 空気の比熱 :0.24〔kcal/kg・deg〕
各部の熱通過率
外壁 $k1=4$〔kcal/㎥・h・deg〕
内壁 $k2=3$〔kcal/㎥・h・deg〕
窓ガラス(一重) $k3=6$〔kcal/㎥・h・deg〕
上下階、隣室は暖房され、廊下の温度を20〔℃〕とする

電熱器の容量をＰ〔kW〕とすれば、

(1)　部屋の発生熱量：H1

蛍光灯：40〔W〕× 30〔灯〕×1=1200〔kcal/h〕
事務機械：1〔kW〕×860=860〔kcal/h〕
電熱器：860P〔kcal/h〕
作業者：20×100=2000〔kcal/h〕

∴H1=1200+860+2000+860P=4060+860P〔kcal/h〕

(2)　部屋から外部へ逃げる熱量：H2

外壁 ,内壁 ,窓ガラス：{4×(3×15)×(24-3)} +{3×(30×3)×(24-20)}+{6×(1.2×4×5)×(24-3)}=3780+1080+3024=7884〔kcal/h〕
部屋の換気：100×1.2×0.24×(24-3)≒605〔kcal/h〕

∴ H2=7884+605=8489〔kcal/h〕

(1),(2)より熱平衡式 H1=H2を作ると

4060+860P=8489
∴ P=(8489-4060)/860≒ 5.15〔kW〕

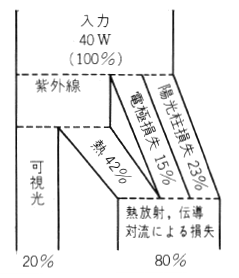
したがって、5.15〔kW〕の電熱器を用いればいいことになります。上記の計算に用いた、電気機器類の発熱量ですが、例えば、40Wの蛍光灯であれば、第4図に示すように、入力電力の約20%が照明に有効な光エネルギーとなるだけで、約32Wの電力は熱損失となり、これに安定器の損失が加わり、蛍光灯1kW、1時間当たり約 1000〔kcal 〕の熱が発生します。