第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、電気に関する基礎理論「直流の電力と電力量」について、解説しています。
電力とは?
電流が 1 秒当たりにする仕事のことを電力(消費電力)といいます。電流がする仕事の仕事率のことです。電力は、仕事率と同じように記号を $P$ で表します。単位はワット(記号:W)を用います。
電力は、「電流×電圧」で求めることができます。オームの法則 $V=RI$ を用いると、次のように表すことができます。
電力の公式
$P =VI=RI^2=\displaystyle \frac{ V^2 }{ R}$[W]
$P$:電力[W]
$V$:電圧[V]
$I$:電流[A]
$R$:電気抵抗[Ω]
電力は、発電所で生み出されたエネルギーをいうこともあれば、電気製品(負荷)などで消費されるエネルギーをいうこともあります。
電力量とは?
電力に時間をかけると、電力の総使用量を求めることができます。この量を、電力量といいます。電力量の記号は $Q$ で表します。単位は[Wh](ワット時)を用います。
電力量の公式
$Q=Pt=VIt=RI^2t=\displaystyle \frac{ V^2t }{ R}$[Wh]
$Q$:電力量[Wh]
$t$:時間[h]
また、1 秒間に 1W の電力をしようしたときの電力量 1Ws は、1J(ジュール)のエネルギー量(仕事量)に置き換えることができます。
電力量 1Ws は、1J(ジュール)のエネルギー量(仕事量)ですので、
1Ws=1J
1h=60×60=3600s ですので、電力量 1Wh に換算すると、
1Wh=3600J=3.6kJ
この換算式から発熱量 $H$[kJ]を求めることができます。
電気に関する基礎理論:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 直流の電力
抵抗 R[Ω]に電圧 V[V]を加えると、電流 I[A]が流れ、P[W]の電力が消費される場合、抵抗 R[Ω]を示す式として、誤っているものは。
イ. $\displaystyle\frac{V}{I}$ ロ. $\displaystyle\frac{P}{I^2}$ ハ. $\displaystyle\frac{V^2}{P}$ 二. $\displaystyle\frac{PI}{V}$
電力の公式より、
$P =VI=RI^2=\displaystyle \frac{ V^2 }{ R}$
イ,ロ,ハの式は導きだすことができます。したがって、二が誤りです。
答え(二)
2008年(平成20年)問4
問2 熱量に関する問題①
電線の接続不良により、接続点の接触抵抗が0.2[Ω]となった。この電線に10[A]の電流が流れると、接続点から1時間に発生する熱量[kJ]は。
ただし、接触抵抗の値は変化しないものとする。
イ. 72 ロ. 144 ハ. 288 二. 576
電力量の公式より、
$Q=RI^2t=0.2×10^2×1=20$[Wh]
発熱量 $H$[kJ]は、
$H=20×60×60=72$[kJ]
答え(イ)
2008年(平成20年)問3
2012年(平成24年)下期 問3 類似
2013年(平成25年)下期 問4
2016年(平成28年)上期 問4 類似
2018年(平成30年)上期 問4 類似
問3 熱量に関する問題②
消費電力が 500[W]の電熱器を、1時間30分使用した時の発熱量[kJ]は。
イ. 450 ロ. 750 ハ. 1800 二. 2700
1時間30分は、1.5h ですので、電力量は、
$Q=500×1.5=750$[Wh]
発熱量 $H$[kJ]は、
$H=750×60×60=2700$[kJ]
答え(二)
2011年(平成23年)上期 問3 類似
2014年(平成26年)下期 問1
2017年(平成29年)下期 問4 類似
2019年(令和元年)下期 問3
問4 熱量に関する問題③
電熱器により、60 kg の水の温度を20 K 上昇させるのに必要な電力量[kW·h]は。
ただし,水の比熱は 4.2 kJ/(kg·K) とし、熱効率は 100 % とする。
イ. 1.0 ロ. 1.2 ハ. 1.4 二. 1.6
60 kg の水の温度を 20 K 上昇させるのに必要な熱量は、
4.2 × 60 × 20 = 5040 kJ
これを電力量に換算すると、
5040/3600 = 1.4 kW·h
答え(ハ)
2012年(平成24年)上期 問4
2015年(平成27年)下期 問4
2018年(平成30年)下期 問4
2019年(令和元年)上期 問3
問5 消費電力
図のような回路で、電流計Aは10[A]を示している。抵抗Rで消費する電力[W]は。
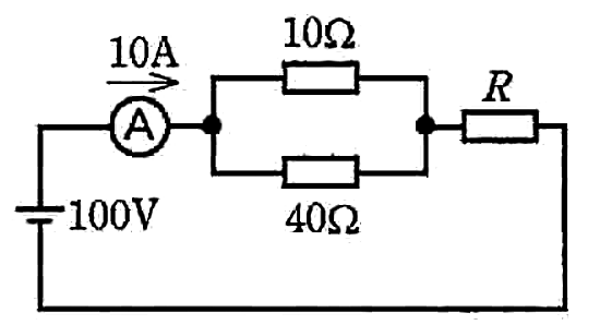
イ. 160 ロ. 200 ハ. 800 二. 1000
まず、10Ωと40Ωが並列になっている箇所の合成抵抗を求めると、
$ R=\displaystyle \frac{ 10×40}{ 10+40}=8[Ω]$
全体の抵抗は、オームの法則より、
100[V]=10[A]×全体抵抗
より、全体抵抗=10Ωなので、Rの部分の抵抗値は、R=10-8=2[Ω]となります。
また、Rの部分にかかる電圧は、
Rの電圧=10[A]×2[Ω] なので、Rの電圧=20Vとなります。
ゆえに、Rの部分で消費する電力は、
Rの電力=10[A]20[V]=200W
答え(ロ)
2012年(平成24年)下期 問1



