第二種電気工事士の筆記試験に初心者の方でも簡単に独学で合格する勉強方法を紹介しています。第二種電気工事士の筆記試験は、過去問から繰り返し出題されていますので、出題分野毎に過去問をまとめて解くことで、効果的な勉強方法となります。このページでは、電気に関する基礎理論「オームの法則と合成抵抗」について、解説しています。
オームの法則
電流の流れにくさを表すことを電気抵抗(抵抗)といいます。抵抗の単位はオーム(記号:Ω)です。 抵抗が小さいと電流は流れやすくなり、抵抗が大きいと電流は流れにくくなります。
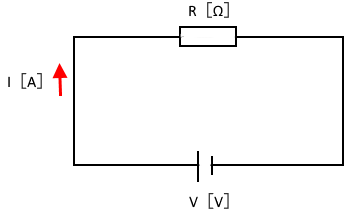
電気回路では、電圧,電流,電気抵抗間には、次のような関係があります。
オームの法則
$V=IR$
$V$:電圧[V]
$I$:電流[A]
$R$:電気抵抗[Ω]
短絡と開放
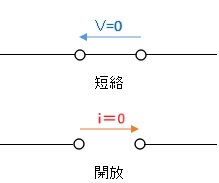
2点間の導線を直接結ぶことを短絡(ショート)といい、2点間になにも接続しないことを開放(オープン)といいます。短絡した2点間の電圧は 0[V]になり、開放した2点間を流れる電流は 0[A]になります。
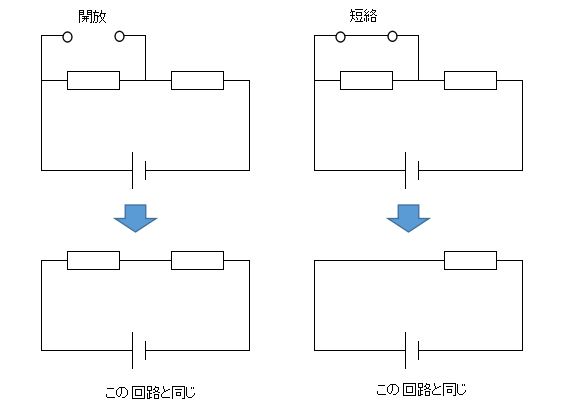
ここで注意が必要なのが、短絡した2点間の電流は 0[A]になるとは限りません。また開放した2点間の電圧は 0[V]になるとは限りません。
開放と短絡
分流と分圧
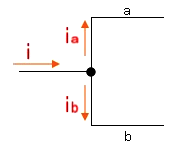
電流 $i$ が流れている導線がaとbに枝分かれしている場合、枝分かれしたそれぞれの導線を流れる電流を $i_a$,$i_b$とすれば、
$i=i_a+i_b$
の関係式が成立します。このように電流が分岐することを分流といいます。
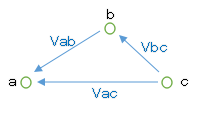
点bの電圧を基準にした点aの電圧を $V_{ab}$、点cを基準にした点bの電圧を $V_{bc}$ とすると、点cを基準にした点aの電圧 $V_{ac}$ は、
$V_{ac}=V_{ab}+V_{bc}$
の関係式が成立します。このように電圧を分けることを分圧といいます。
合成抵抗
抵抗の直列接続
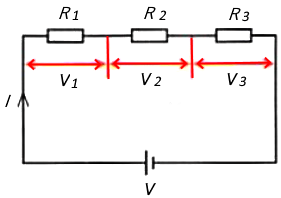
複数の抵抗を直列に接続した場合の合成抵抗を考えます。直列接続では、回路は枝分かれしませんので、すべての抵抗には同じ電流が流れます。
各抵抗にかかる電圧と電流をオームの法則を使って表せば、
$V_1=IR_1$,$V_2=IR_2$,$V_3=IR_3$
電源電圧 $V$ は各抵抗にかかる電圧の和に等しいので、
$V=V_1+V_2+V_3=I(R_1+R_2+R_3)$
合成抵抗 $R$ は以下の式で表せます。
直列接続の合成抵抗
$R=(R_1+R_2+R_3)$
抵抗を直列に接続することは抵抗の長さを増やすことに相当します。抵抗は長さに比例しますので、直列の合成抵抗は増えます。
抵抗の並列接続
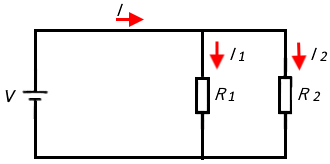
複数の抵抗を並列に接続した場合の合成抵抗を考えます。並列接続では、各抵抗にかかる電圧は電源電圧と同じ電圧がかかります。
各抵抗にかかる電圧と電流をオームの法則を使って表せば、
$I_1=\displaystyle \frac{ V}{ R_1 },I_2=\displaystyle \frac{ V}{ R_2 }$
回路に流れる電流 $I$ は各抵抗に流れる電流の和に等しいので、
$I=I_1+I_2=\displaystyle \left(\frac{ 1}{ R_1 }+\frac{ 1}{ R_2 }\right)V$
合成抵抗 $R$ は以下の式で表せます。
並列接続の合成抵抗
$\displaystyle \frac{ 1}{ R }=\displaystyle \frac{ 1}{ R_1 }+\frac{ 1}{ R_2 }$
抵抗を並列に接続することは抵抗の断面積を増やすことに相当します。抵抗は断面積に反比例しますので、並列の合成抵抗は減ります。
2個の抵抗を並列接続した場合は、次のように変形して覚えておくと計算が楽になります。
$\displaystyle \frac{ 1}{ R }=\displaystyle \frac{ 1}{ R_1 }+\frac{ 1}{ R_2 }$ ⇒ $ R=\displaystyle \frac{ R_1R_2}{ R_1+R_2 }$
2個の抵抗の並列接続の合成抵抗は、和分の積と覚えておきましょう!
また、2個の抵抗が、例えば $R$ で同じ値の場合の合成抵抗は、
$\displaystyle \frac{ R×R}{ R+R }=\frac{ R}{ 2 }$
となります。元の値の半分になりますので、覚えておくと計算が楽になります。
抵抗の直並列接続
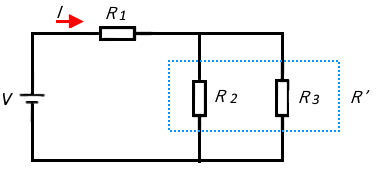
直列に接続と並列接続が組み合わされた回路の合成抵抗の求め方を考えます。$R_2$ と $R_3$ の並列部分の合成抵抗 $R’$ を求めます。
$R’=\displaystyle \frac{ R_2R_3}{ R_2+R_3 }$
$R_1$ と $R’$ が直列に接続されていると考え合成抵抗 $R$ を求めます
$R=R_1+\displaystyle \frac{ R_2R_3}{ R_2+R_3 }$
電気に関する基礎理論:第二種電気工事士 過去問
(財)電気技術者試験センターが作成した第二種電気工事士の筆記試験に出題された問題です。
問1 合成抵抗①
図のような回路で、端子 a – b 間の合成抵抗[Ω]は。
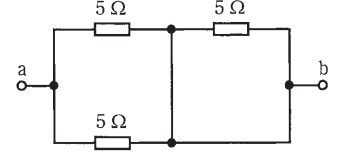
イ. 2.5 ロ. 5 ハ. 7.5 二. 15
右側の並列回路は短絡されていますので、回路図を書きかえると次のようになります。
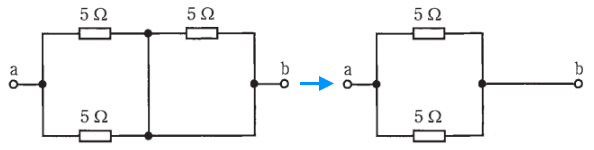
つまり、端子 a – b 間の合成抵抗は、5 Ω と 5 Ω の並列回路の合成抵抗となります。したがって、
$\displaystyle\frac{5}{2}=2.5$[Ω]
答え(イ)
2017年(平成29年)上期 問1
問2 合成抵抗②
図のような回路で、端子 a-b 間の合成抵抗[Ω]は。
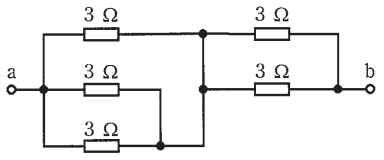
イ. 1.1 ロ. 2.5 ハ. 6 二. 15
2か所ある 3 Ω の並列回路の合成抵抗は 1.5 Ω です。回路図を書きかえると次のようになります。
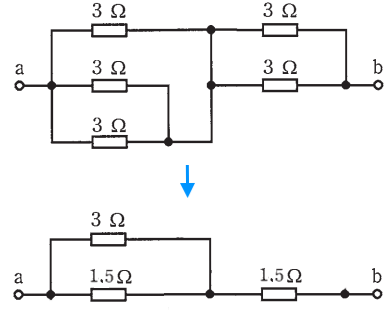
端子 a-b 間の合成抵抗は、
$\displaystyle\frac{3×1.5}{3+1.5}+1.5=2.5$[Ω]
答え(ロ)
2016年(平成28年)上期 問1
問3 合成抵抗③
図のような回路で、端子 a-b 間の合成抵抗[Ω]は。
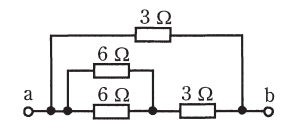
イ. 1 ロ. 2 ハ. 3 二. 4
6 Ω の並列回路の合成抵抗は 3 Ω です。回路図を書きかえると次のようになります。
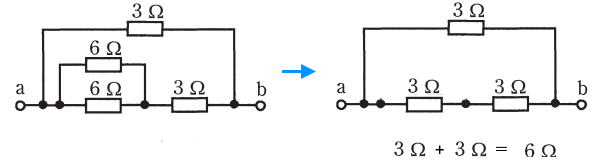
3 Ω と 3 Ω の直列回路の合成抵抗は 6 Ω です。つまり、端子 a – b 間の合成抵抗 は、3 Ω と 6 Ω の並列回路の合成抵抗となります。したがって、
$\displaystyle\frac{3×6}{3+6}=\displaystyle\frac{18}{9}=2$[Ω]
答え(ロ)
2006年(平成18年)問1
2019年(令和元年)下期 問1
問4 合成抵抗④
図のような回路で、端子 a-b 間の合成抵抗[Ω]は。
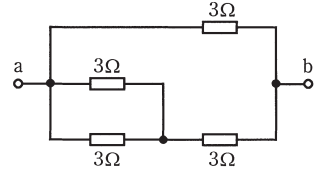
イ. 1.5 ロ. 1.8 ハ. 2.4 二. 3.0
3 Ω の並列回路の合成抵抗は 1.5 Ω です。回路図を書きかえると次のようになります。
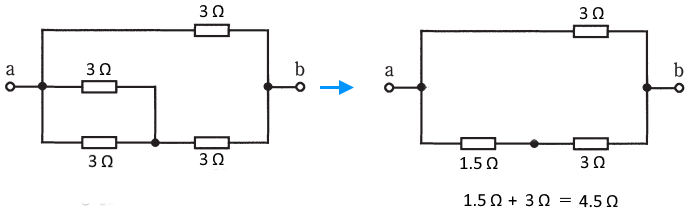
1.5 Ω と 3 Ω の直列回路の合成抵抗は 4.5 Ω です。つまり、端子 a – b 間の合成抵抗 は、3 Ω と 4.5 Ω の並列回路の合成抵抗となります。したがって、
$\displaystyle\frac{3×4.5}{3+4.5}=\displaystyle\frac{13.5}{7.5}=1.8$[Ω]
答え(ロ)
2010年(平成22年)問1
2012年(平成24年)上期 問1
2015年(平成27年)上期 問1 類似問題
問5 合成抵抗⑤
図のような回路で、端子 a-b 間の合成抵抗[Ω]は。
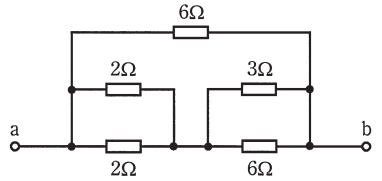
イ. 1 ロ. 2 ハ. 3 二. 4
2 Ω の並列回路の合成抵抗は 1 Ω です。3 Ω と 6 Ω の並列回路の合成抵抗は、
$\displaystyle\frac{3×6}{3+6}=\displaystyle\frac{18}{9}=2$[Ω]
回路図を書きかえると次のようになります。
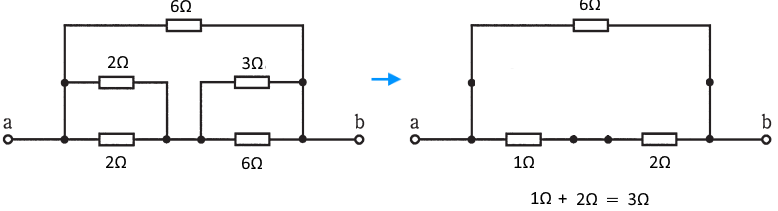
1 Ω と 2 Ω の直列回路の合成抵抗は 3 Ω です。つまり、端子 a – b 間の合成抵抗 は、3 Ω と 6 Ω の並列回路の合成抵抗となり、2 Ω となります。
答え(ロ)
2014年(平成26年)上期 問2
2018年(平成30年)下期 問1
問6 合成抵抗⑥
図のような回路で、スイッチ S1 を閉じ、スイッチ S2 を開いたときの、端子 a-b 間の合成抵抗[Ω]は。
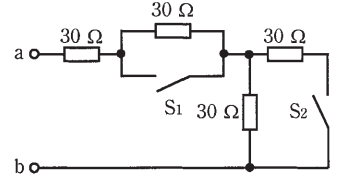
イ. 45 ロ. 60 ハ. 75 二. 120
スイッチ S1 を閉じ、スイッチ S2 を開いたときの等価回路を示します。
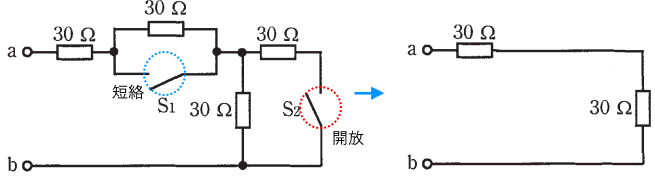
端子 a-b 間は 30 Ω の抵抗の直列回路となりますので、合成抵抗は 30 Ω + 30 Ω = 60 Ω となります。
答え(ロ)
2016年(平成28年)下期 問2
2018年(平成30年)上期 問1 類似
問7 オームの法則①
図のような直流回路に流れる電流 I[A]は。
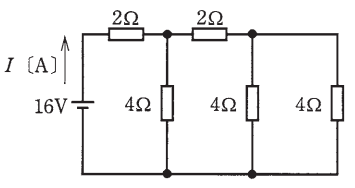
イ. 1 ロ. 2 ハ. 4 二. 8
回路全体の合成抵抗を右側から求めます。
- 4 Ω の並列回路の合成抵抗は 2 Ω です。
- 2 Ω と 2 Ω の直列回路の合成抵抗は 4 Ω です。
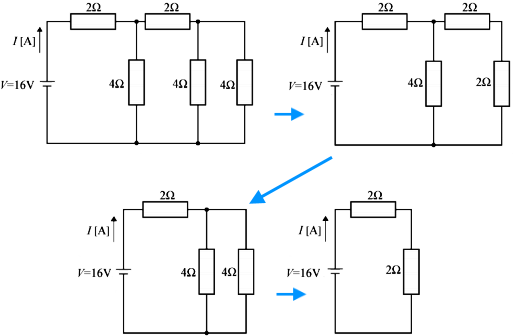
順次計算していくと、回路全体の合成抵抗は 4 Ω になります。回路に流れる電流 $I$[A]は、オームの法則より、
$I=\displaystyle\frac{V}{R}=\displaystyle\frac{16}{4}=4$[Ω]
答え(ハ)
2014年(平成26年)下期 問2
問8 オームの法則②
図のような回路で、スイッチ S を閉じたとき、a-b 端子間の電圧[V]は。
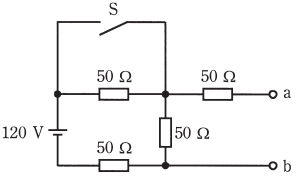
イ. 30 ロ. 40 ハ. 50 二. 60
スイッチ S を閉じたときの等価回路を示します。
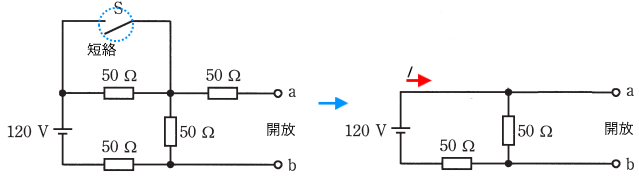
電源から流れる電流を $I$ [A]とすると、回路全体の合成抵抗は、R = 50+50=100Ω ですので、回路に流れる電流 $I$[A]は、オームの法則より、
$I=\displaystyle\frac{V}{R}=\displaystyle\frac{120}{100}=1.2$[A]
a-b 端子間の電圧は、1.2 A の電流が流れる 50 Ω の抵抗に発生する電圧ですので、オームの法則より、
$V=IR=1.2×50=60$ [V]
答え(ハ)
2011年(平成23年)上期 問2 類似問題
2015年(平成27年)下期 問1
2019年(令和元年)上期 問1
問9 オームの法則③
図のような直流回路で、a-b 間の電圧[V]は。
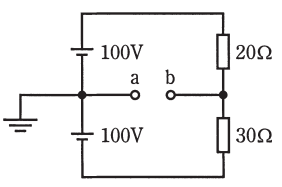
イ. 10 ロ. 20 ハ. 30 二. 40
電源から流れる電流を $I$ [A]とすると、回路全体の合成抵抗は、R = 20+30=50Ω です。電源電圧を合成すると、100-(-100)=200 V ですので、回路に流れる電流 $I$[A]は、オームの法則より、
$I=\displaystyle\frac{V}{R}=\displaystyle\frac{200}{50}=4$[A]
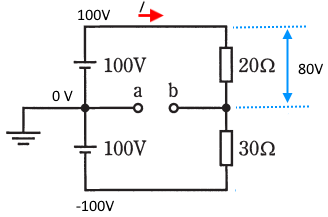
20 Ω の抵抗に発生する電圧は、4 A の電流が流れていますので、 オームの法則より、
$V=IR=4×20=80$ [V]
上側の回路だけを考えると、100 V の電源電圧から 80 V の 20 Ω の抵抗に発生する電圧を引いてやると、a-b 間の電圧[V]になります。したがって、
$100-80=20$[V]
答え(ロ)
2009年(平成21年)問1
2013年(平成25年)上期 問1
2017年(平成29年)下期 問1 類似問題
問10 オームの法則④
図のような回路で、電流計(A) の値が 1A を示した。このときの電圧計(V)の指示値[V]は。
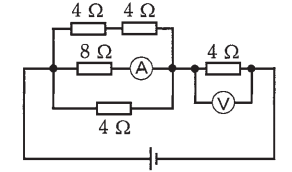
イ. 16 ロ. 32 ハ. 40 二. 48
図のように、各回路に流れる電流を $I$,$I_1$,$I_2$,$I_3$[A]とします。
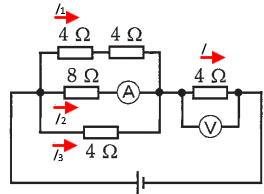
題意より、電流計(A) の値が 1A を示したとありますので、$I_2=1$[A]となります。この 8Ω の抵抗の両端の電圧は 1A × 8Ω = 8V となります。
また、並列回路部分の電圧が 8V ですので、$I_1$,$I_2$[A]は、オームの法則より、
$I_1=\displaystyle\frac{8}{4+4}=1$[A]
$I_2=\displaystyle\frac{8}{4}=2$[A]
$I$[A]は、$I=I_1+I_2+I_3=1+1+2=4$[A]の関係が成立しますので、電圧計(V)の指示値 $V$[V]は
$V=4×4=16$[V]
答え(イ)
2013年(平成25年)下期 問1
2016年(平成28年)下期 問1 類似問題



