これだけは知っておきたい電気設備の基礎知識をご紹介します。このページでは「電力の使われ方」について、維持管理や保全などを行う電気技術者の方が、知っておくとためになる電気の基礎知識を解説しています。
電力はどのように使われているか
電力は電気のもつ特性を利用して、熱 ,光 ,電動力等に変換されて使用されるわけですが、その場合の電力のエネルギー変換技術、つまり電力応用技術にはどのようなものがあるかを、代表的なものについて説明します。
電熱
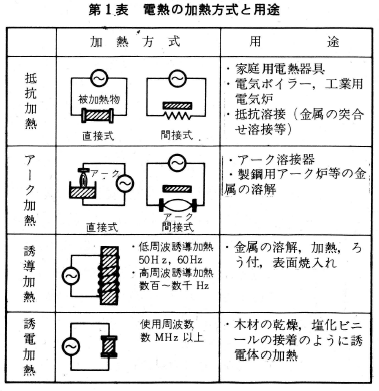
抵抗加熱
抵抗に電流が流れると、ジュール熱が発生しますが、この熱を利用するものが抵抗加熱です。
アーク加熱
電極を突合わせておいて、電圧を加え、この電極を引き離すとアークを生じ、適当な電圧と電源容量があれば、連続的にアーク放電を起こすことができます。アーク放電においては、電子の衝突と熱電離により、空気中の分子、原子は電離され、非常に高温 (アーク柱で 5000K~ 6000K)と光を発します。このアークの高温を利用するのが、アーク加熱です。
誘導加熱
加熱コイルの中に導電性の被加熱物を入れ、加熱コイルに交流電圧を加えると、コイルに生じる交番磁界により、被加熱物には誘導電圧を生じ、うず電流が流れます。このうず電流による抵抗損に交番磁界によるヒステリシス損が加わり、被加熱物は内部より加熱されます。また、加える交流の周波数を高くしていくと、うず電流は表面に集中し (表皮効果)、金属の表面焼入などを行うことができます。
誘電加熱
誘電率の高い物質 (電気的に絶縁物で、誘電体という)を、電極ではさみ、これに高周波の交流を加えると、誘 電体内部の分子の有する一対の正負の電気が、高周波電界により回転し、そのとき生じる摩擦力により物体は発熱します。この熱を誘電体損失熱といい、電子レンジはその応用例です。
照明
白熱電球は、フィラメントに電流を流して、これを高温に熱し (2800~ 3000℃)、高温度のフィラメントからの温度放射による光を利用しています。また、フィラメント温度を 2200~ 2500℃ にすると、赤外線が多く放射され、塗装乾燥器等に用いられています。
蛍光灯、水銀灯などの放電灯は、低圧あるいは高圧ガス中のグロー放電を利用し、このグロー放電部より出る紫外線などの光を、直接あるいは蛍光物質にあて可視光に変換して、照明に利用しています。
電動力
電動機を機械などの動力源として利用するものであり、ポ ンプ,エレベーター,各種産業用機械など、その応用は多方面にわたります。なお、電力と機械エネルギーの変換は電流により生じる磁界により行われ、磁界は電気 エネルギーと機械エネルギーを結ぶ継手といえます。電気エネルギーは電流によって運ばれ、電流を流す力となるものが電圧です。
電気化学
電力を電気化学に応用したものは数多くありますが、身近なものとして、化学変化のエネルギーを電気エネルギーに変換する蓄電池があります。工業的には、比較的大電力を消費する電気分解が代表的なものであり、水の電気分解 ,アルミニウムの製造などに利用されています。
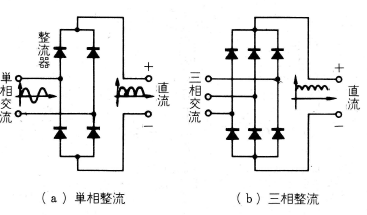
直流電力
蓄電池 ,電気化学 ,直流電動機 ,テレビなどの弱電機器などは直流を使用しますので、交流電力の直流電力への変換が行われます。この直流への変換は、小容量の場合は単相交流が、直流大電力の場合は三相交流が整流して使われています。
冷凍機と電力
電力は、熱 ,電動力などに変換されて利用されていますが、冷凍機の場合を例にとって、電力がどのように使われているか説明してみます。
第2図に圧縮式冷凍機の冷凍サイクルとモリエル線図を示します。蒸発器で $Q_A=(Q_2-Q_1)A$ の熱を吸収した冷媒ガスは、電動式圧縮機で断熱圧縮され、凝縮器で $Q_B=(Q_3-Q_1)A=Q_A+860W_o$ の熱を放熱して、冷媒ガスは液化し、膨張弁で断熱膨張 、再び蒸発器に到ります。ここで $A$ は冷媒流量〔kg/h〕です。
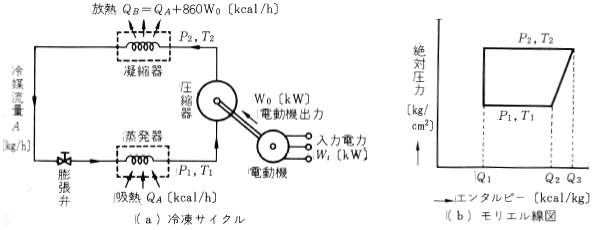
この冷凍サイクルで、電動力 $W_o$ 、 冷媒ガスを圧縮するのに使われており、圧縮された冷媒ガスは圧力 $P_1$ , 温度 $T_1$ から圧力 $P_2$, 温度 $T_2$ に上昇し、モリエル線図でみると、1時間に $(Q_3-Q_2)A$〔kcal〕の内部エネルギー (エンタルピー)が増加します。
つまり、電動機に入力された電力 $W_i$〔kW〕は、電動圧縮機械力 $W_o=\displaystyle \frac{W_i}{ηw} $〔kW〕 ( $ηw$:電動機効率)に変換され、冷媒ガスを圧縮する仕事 $3.6×10^6W_o$ 〔J/h〕(熱量に換算すると $860W_o$〔 kcal/h〕 )を行い、結果的には冷媒ガスの内部エネルギーを $(Q_3-Q_1)A$ 〔 kcal/h〕増加するのに使われています。したがって $860W_o$ は $(Q_3-Q_2)A$ に相当します。
ここで、$ε=\displaystyle \frac{Q_A }{860W_o}=\displaystyle \frac{Q_2-Q_1}{Q_3-Q_2}$ を冷凍機の成績係数といい、普通 3前後の値です。これは、電動機効率を無視すると、電力量 $W_i$〔kWh〕に相当する熱量 $860W_i$〔kcal〕 を利用して、蒸発器で $ε× 860W_i$〔kcal〕の熱を吸収できることを示しています。
冷房負荷と冷凍機の電動機出力
冷房負荷、つまり蒸発器で吸収する熱量を$Q_A$〔kcal/ h〕、冷凍機の成績係数を $ε$ 、圧縮効率を $ηp$、機械効率を $ηi$、電動機所要出力を $W_o$〔kW〕とすれば、
$Q_A =860W_o×ε×ηp×ηi$
が成り立ちますので、
電動機所要出力 $W_o=\displaystyle \frac{Q_A}{860εηpηi} $〔kW〕
電動機入力 $W_i= \displaystyle \frac{W_o}{ηw}$〔kw〕
で表わすことができます。この式で注意することは、$W_i$〔kW〕が $Q_A$〔kcal/ h〕に相当するのではな く、電動機出力 $W_o$〔kW〕で 1 時間冷凍機を運転した場合 (電力量にして $W_i$〔 kWh〕 ) に、蒸発器で $Q_A$〔kcal〕の熱を吸収できるということです。
また、凝縮器で発生した熱を利用すれば、暖房を行なうことができます。この場合の成績係数は $ε=\displaystyle \frac{Q_B}{860}W_o>1$ で表わされ、蒸発器で低位の熱 (空内の発生熱のように温度、圧力の低い熱)を吸収し、凝縮器で電動機入力の $ε$ 倍の熱を暖房に利用することができ、抵抗式電熱器等に比べ、省エネルギーにマッチした、非常に効果的な方法となります。なお、第2図のようなサイクルをヒートポンプサイクルともいいます。
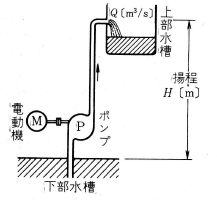
ポンプの電動力
第3図に示すような、揚程 $H$〔m〕、流 量 $Q$〔㎥/s〕の揚水ポンプを考えてみます。この場合、電動力は、1秒間に $Q$〔㎥〕の水を $H$〔m〕の高さに揚水するのに使われたのですが、これを流体側よりみれば、位置エネルギーが 1秒間に $WQH$ 〔kgm〕増加したことになります ($W$:流体の単位体積当りの重量で、水の場合 1000〔kg/㎥〕 )。 つまり、電力は、ポンプを介して、水の位置エネルギーの増加 $WQH$〔kgm/s〕 $=9.8WQH$〔J/s〕 に消費されたことになり、この $9.8WQH$ 〔J/s〕は、ポ ンプの仕事率、つまり電動機出力に相当します。したがって、電動機出力 $P$ は、ポンプ効率を無視すると、
$P=9.8WQH$〔J/s〕$ =9.8WQH$〔W〕$=9.80QH×10^3$〔W〕$=9.80QH$〔kw〕
で表わすことができます。